高原变海拔对柴油机缸压信号的影响分析

甘庆良，刘震涛，张宇

(浙江大学能源工程学院动力机械及车辆工程研究所，浙江 杭州 310027)

我国幅员辽阔，地形复杂，高原面积占比很大。某设备在高原变海拔环境下行驶时，由于进气量减少，过量空气系数下降[1]，发动机燃烧恶化，出现了活塞烧蚀、缸套拉缸及缸盖有麻点等一系列故障。针对缸盖火力面出现麻点这一故障现象，损伤部位的检测结果表明，其表面未发生金属熔融现象，金相分析发现铝硅合金中硅成分减少，即产生晶体分离。而对缸压信号进行分析时，并未发现最高燃烧压力升高，燃烧压力波动幅值增大等现象。基于此，针对出现此故障的原因提出了以下假设：随着海拔上升，缸内燃烧异常，压力出现急剧波动，即压力波动频率剧增，且随着海拔越来越高，波动越来越剧烈，即高频成分比例增大。为此，利用可以模拟变海拔条件的单缸机试验台架进行单缸机试验，采集不同海拔下的缸内压力，并对数据进行分析，判断该假设是否成立 。

缸压信号作为反映柴油机燃烧状况极其重要的信号，包含了大量的信息，可以充分反映内燃机工作过程中的压缩过程、点火过程及燃烧放热过程等[2]。然而，从燃烧分析仪采集得到的缸压信号，在时域上，不论是压力峰值还是信号不平稳程度，都难以看出其内部波动情况，因此，无法判断其与海拔的相关性。基于此，对采集到的信号进行分解剥离，分析不同海拔高度下缸压信号中不同频次成分的占比。鉴于缸压信号的非线性、不平稳特点，本研究采用希尔伯特-黄变换(HHT)对缸压部分信号先进行集平均经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)，将每个工况下的缸压信号按照不同频率分解出来，针对不同海拔下的分解结果，求出其不同频率成分下的功率谱密度，再进行比较分析。

1 单缸机试验方案

1.1 燃烧分析仪

KiBox 燃烧分析仪可以用于发动机台架标准稳态燃烧分析——燃烧热力学计算、示功图、爆震分析、压力升高率分析、瞬时放热率和累计放热率分析，并得到峰值。其部分参数见表1。其中，转角分辨率是决定采样频率的最关键参数。

表1 燃烧分析仪参数

1.2 试验工况

针对某重型柴油机在高原工况下存在的问题，设计并搭建单缸机的试验台架，通过改变试验过程中的进气压力，模拟发动机在高原环境下海拔的升降[1]。

主要设备包括缸径150 mm单缸机、水力测功机、AVL TGS1760油耗仪、流量计、曲轴及凸轮轴转速传感器、温度传感器及进气压力高原模拟试验台等。单缸机最大转速2 200 r/min，热电偶布置在缸盖的火力面上以及缸套外侧，缸内压力传感器通过燃烧分析仪输出缸内压力信号。试验设定6个海拔条件，进行了不同海拔下模拟高原环境的单缸机试验，得到了不同工况下的缸内压力。试验工况见表2。

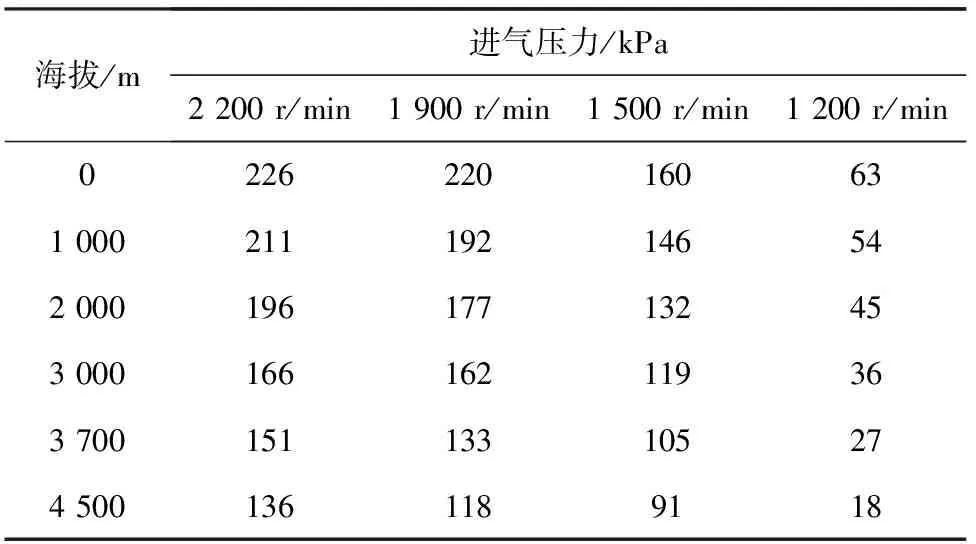
表2 进气压力与海拔对应关系

2 EEMD方法原理

2.1 本征模态函数

本征模态函数(Intrinsic mode functions，IMF)必须满足两个条件：1)极值点数与过零点数至多相差一个；2)在任意一点，由局部极大值构造的包络线与局部极小值构造的包络线的平均值为0[3]。

2.2 经验模态分解

经验模态分解能把非线性、不平稳信号分解成一系列本征模态函数，这是基于EMD的两个假设：1)任何复杂的数据信号都是由一系列简单的本征模态函数组成；2)任意两个本征模态函数之间是互相独立的，即满足相互正交[4]。

对于一个复杂信号，其经验模态分解的步骤如下：

1) 记原始信号为x(t),初始化,令r0(t)=x(t),i=1。

3)ri(t)=-ri-1(t)-IMFi(t)。

4) 若ri(t)极值点数不少于2个，则i=i+1，转到步骤2，否则，分解结束，ri(t)是残余量。

2.3 集平均经验模态分解

集平均经验模态分解(EEMD)是EMD的改进版，EEMD采用了噪声辅助分析方法，其分解原理是当附加的白噪声均匀分布在整个时频空间时，该时频空间就由滤波器组分割成的不同尺度成分组成。

当信号加上均匀分布的白噪声背景时，不同尺度的信号区域将自动映射到与背景白噪声相关的适当尺度上去。既然在每个独立的测试中噪声是不同的，当使用足够测试的全体均值时，噪声将会被消除。全体的均值最后将会被认为是真正的结果，随着测试的增多，附加的噪声被消除了，唯一持久稳固的部分是信号本身[6]。

3 分解结果分析

3.1 1 500 r/min，160 kPa工况

以1 500 r/min，进气压力160 kPa工况为例。原始信号见图1，其中，横坐标为时间，原始信号为101个循环，需要8.08 s，纵坐标是缸内压力，燃烧分析仪每0.1°采集一个压力数据，发动机曲轴转2 r(720°)完成一个循环，因此每个循环有7 200个数据点，101个循环一共727 200个数据点。由于采集循环数量较多，信号叠加在一起比较密集，图片难以绘制清晰，考虑到缸压信号的循环特性，故本节图片均展示前10个循环一共72 000个数据点，即0～0.808 s时间内的数据。

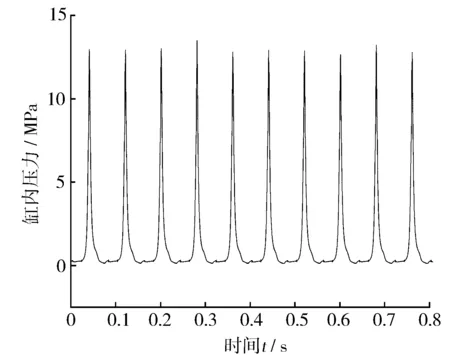
图1 1 500 r/min，160 kPa工况原始缸压数据

按照EEMD理论方法，对原始信号添加幅值为0.2的白噪声，并进行400次叠加运算，分解以后得到了包括白噪声在内的19个组分。首先，需要判断这19个组分在时域内是否相互独立，即是否满足正交性，是否需要过滤掉增加的白噪声成分。之后，略去分解剩下的余项，最终得到了满足IMF条件的6个本征模态函数(见图2)[8]。

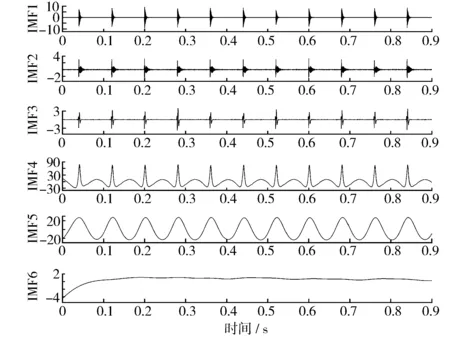
图2 IMF信号图

对得到的6个IMF分别计算出相应的瞬时频率和振幅，结果见图3和图4。由图4可知，IMF1，IMF2，IMF3这3个IMF属于高频成分，IMF4，IMF5，IMF6这3个IMF属于低频成分。从图5可以看到，与图4相对应，能量(图上的颜色明亮程度代表能量高低。)基本集中在IMF4和IMF5这两条频率曲线中，其中以12.5 Hz这条频率线最为突出。

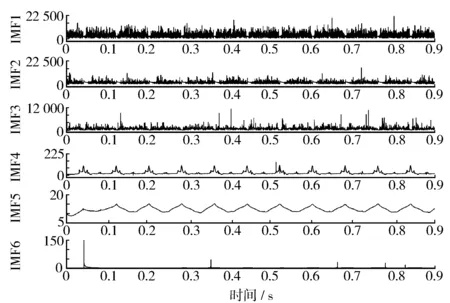
图3 IMF频率图

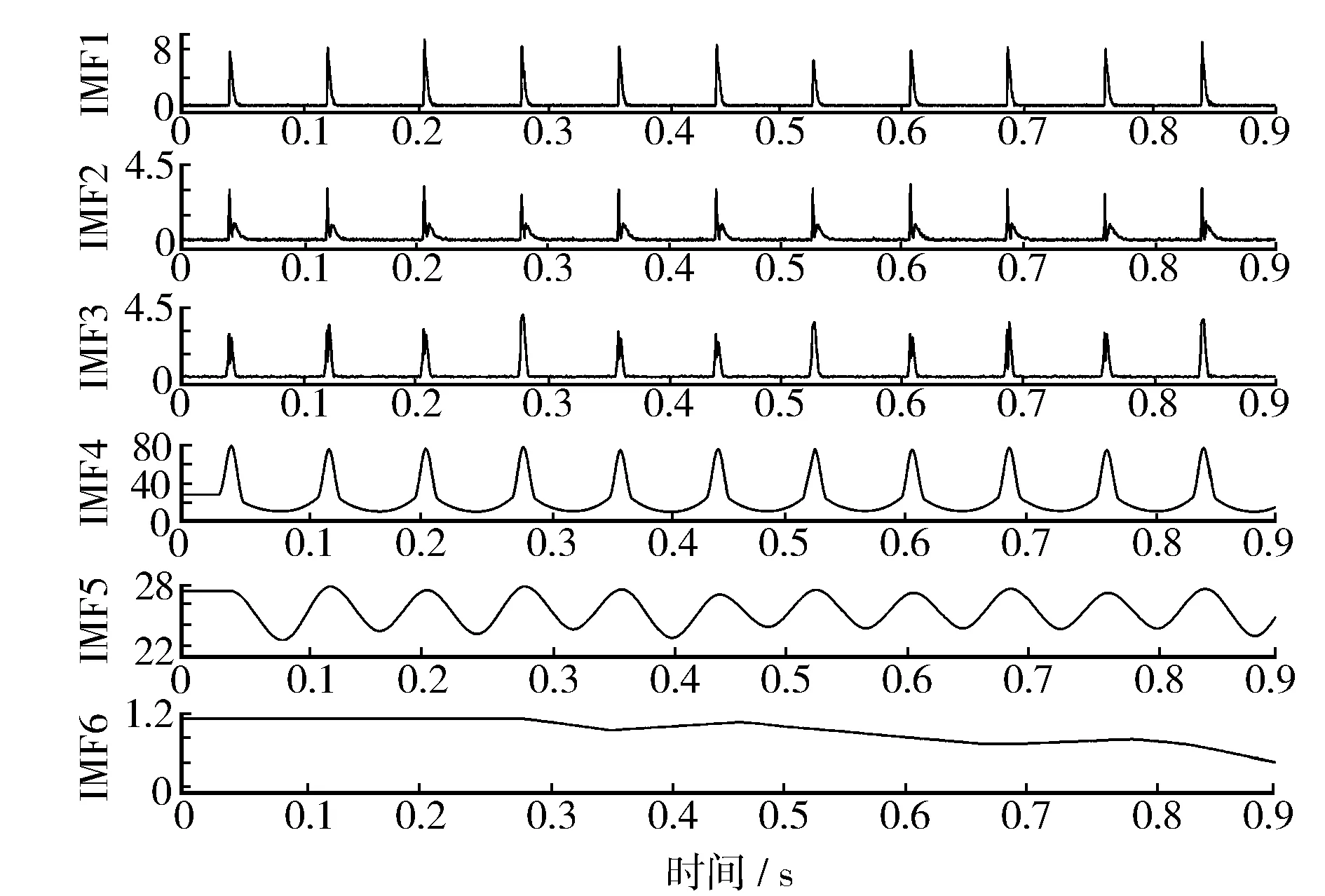
图4 IMF振幅图

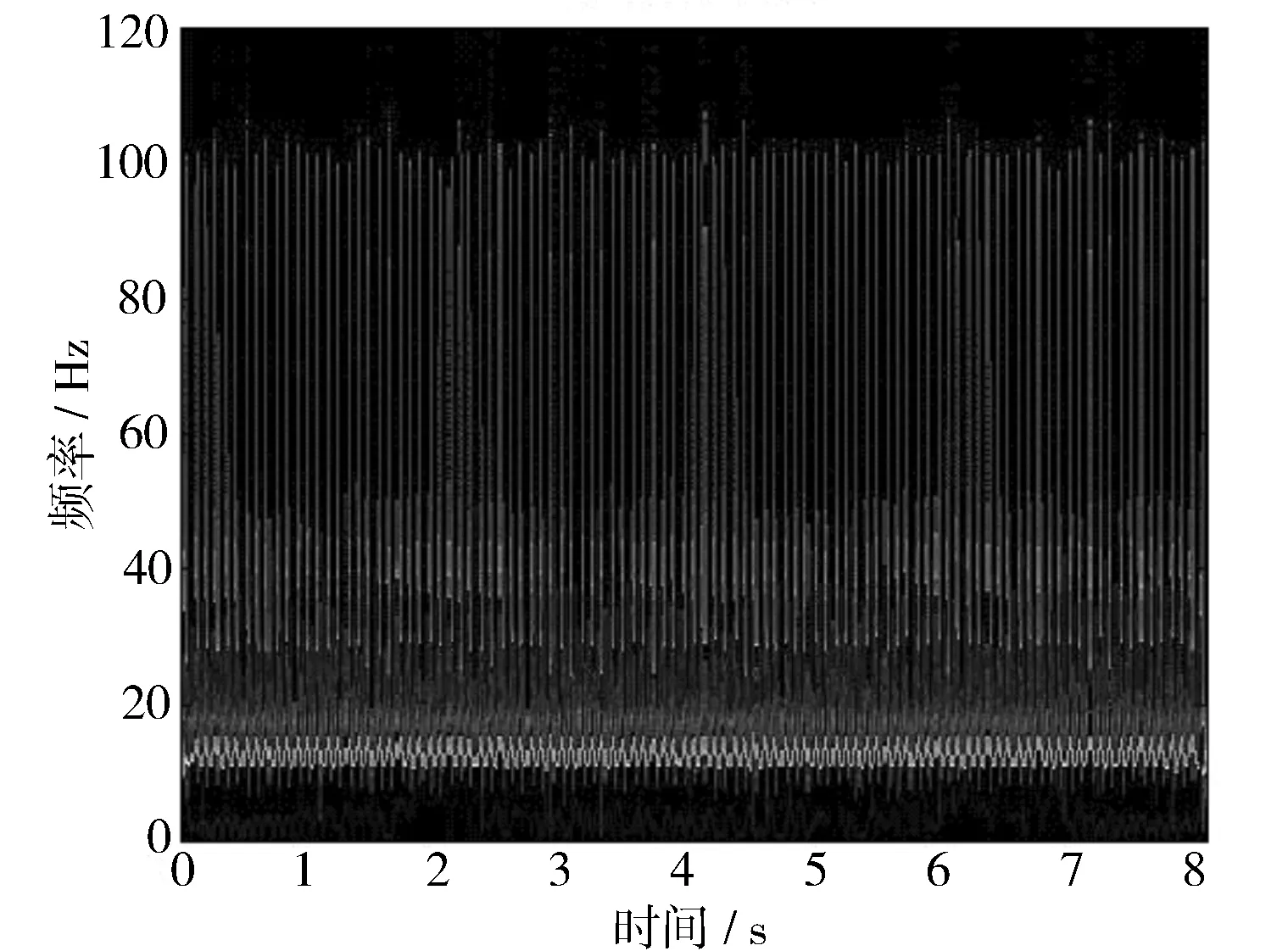
图5 时频图

3.2 1 500 r/min，不同海拔工况

经过EEMD分解，可以看到缸压信号的高频和低频成分被很好地分割开，观察振幅图可以看到，低频成分的能量曲线非常规则平稳，且幅值波动不太大。反观高频成分，频率和幅值的波动都异常剧烈，而这部分能量极有可能是造成缸压波动剧烈的原因[9]。因此，针对不同工况下分解得到的IMF高频低频成分，求取功率谱密度，并进行对比分析[10]。在单缸机试验过程中，进气压力下降到91 kPa，排气温度超过700 ℃的工况，不符合试验安全要求，且与前5个海拔工况相比，此工况对比意义不大，因此在对比分析的过程中不考虑此工况。结果见图6。

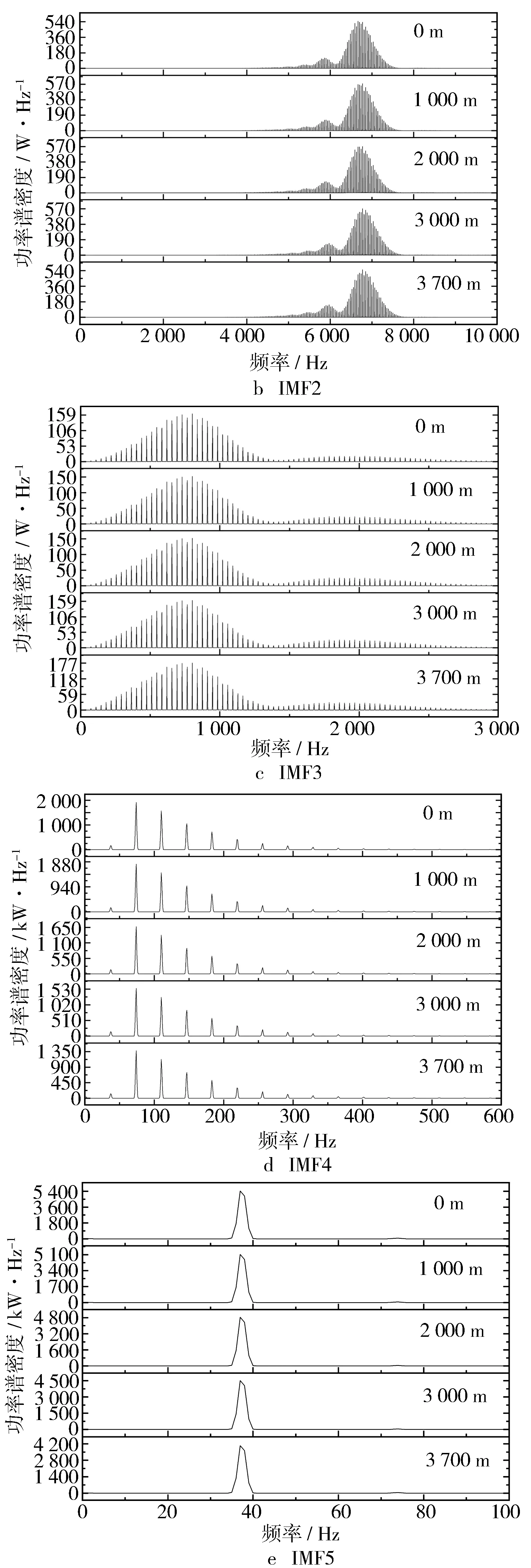
图6 1 500 r/min，不同工况功率谱密度对比

从以上各图的变化来看，功率谱密度的峰值所对应的频率在不断左移，即频率不断降低，且所对应频率与之前求得的IMF频率图中的频率相对应。同样，先从能量高的低频成分开始分析,将图6d与图6e放大，其峰值频段的对比见图7。

观察这两部分低频能量，可以看到，随着进气压力的下降，即海拔的上升，低频段的功率谱密度逐渐减小，这表明，随着海拔上升IMF的低频段的能量在逐渐减小，缸压信号的能量在逐渐降低。

图7 低频成分功率谱密度峰值对比

高频成分峰值频段的对比见图8。由图8可以看到，IMF1和IMF2的高频能量并没有严格按照海拔排列，但是，进气压力119 kPa和105 kPa(对应的海拔为3 000 m和3 700 m)条件下，对应的功率谱密度始终高于其他3个工况。

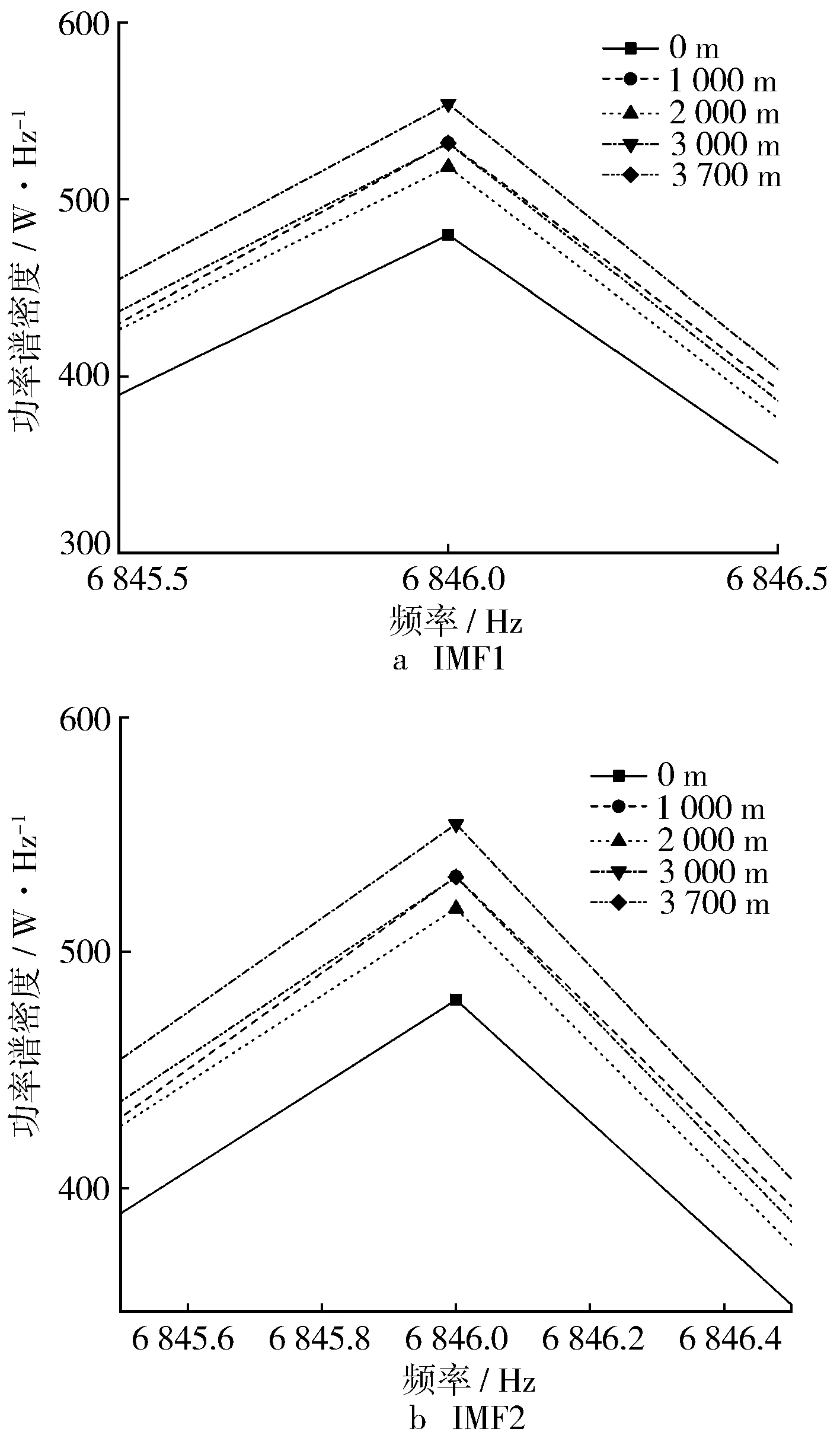
图8 高频成分功率谱密度峰值对比

由图8可知，海拔超过3 000 m以后，高频率段的能量反而高于平原工况。结合低频率段的功率谱密度对比分析，可以得出以下结论：随着海拔上升，对于分解得到的IMF，其低频段的能量在逐渐降低，高频段的能量变化没有明显规律，然而，当海拔超过3 000 m以后，高频信号能量均高于低海拔工况。

3.3 2 200 r/min和1 900 r/min工况

同样地，对2 200 r/min及1 900 r/min转速下采集到的缸压信号进行分解，结果见图9和图10。

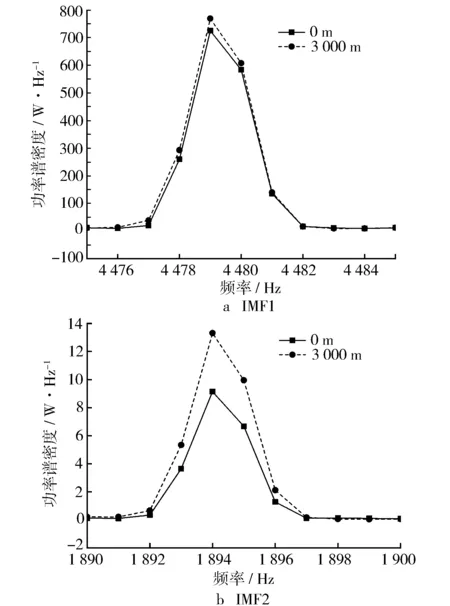
图9 2 200 r/min，IMF1和IMF2功率谱密度对比

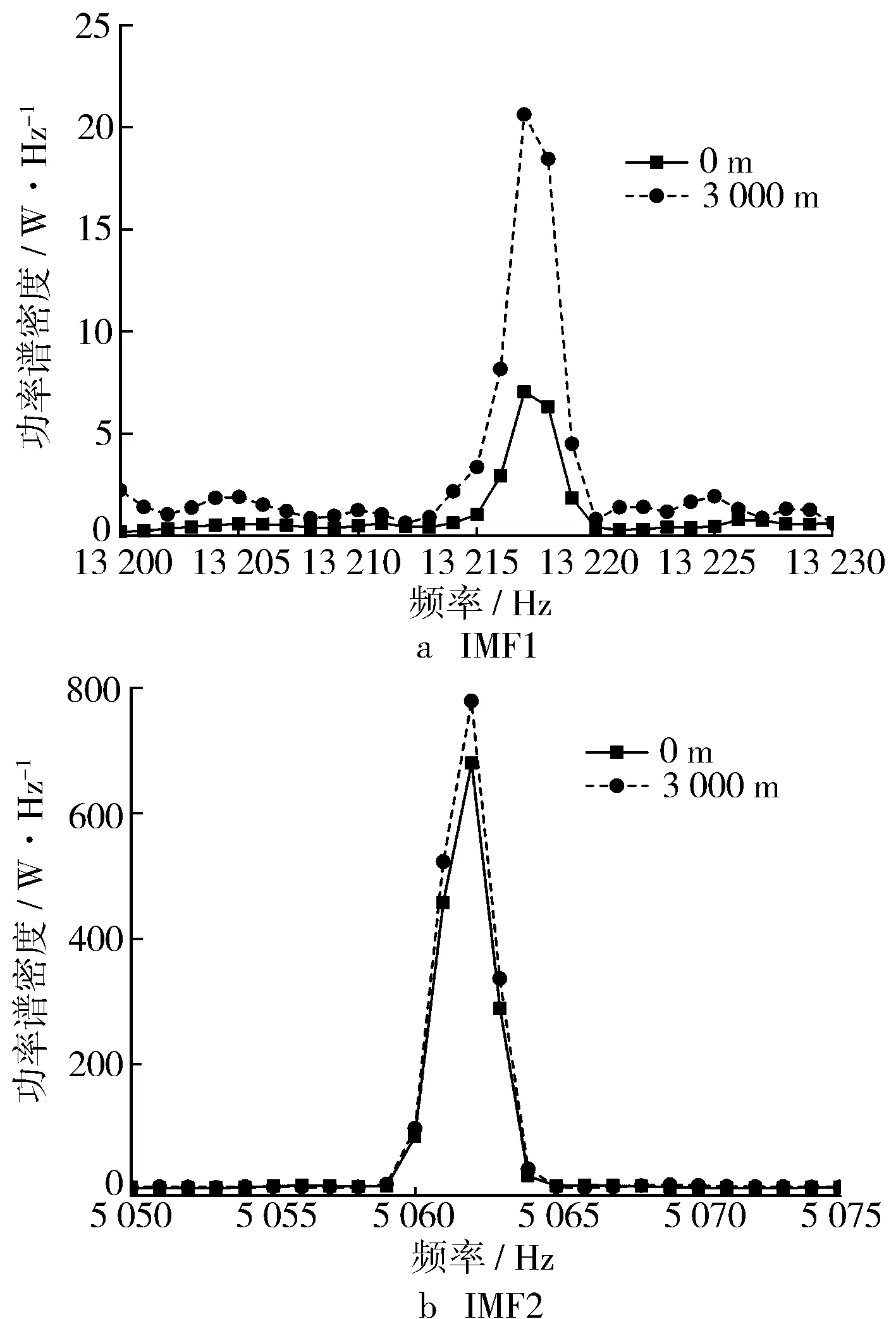
图10 1 900 r/min，IMF1和IMF2功率谱密度对比

与1 500 r/min工况相似，在2 200 r/min和1 900 r/min工况下，分解得到的高频成分在海拔3 000 m的能量大于平原地区，说明随着海拔上升，高频成分的能量在逐渐增强。

4 结论

a) 缸压信号的频域分析相对于时域分析，可得到更加有效的信息；

b) 缸压信号的能量随着海拔上升逐渐降低，然而，高频段部分的能量在海拔3 000 m以上却出现明显的上升；

c) 当海拔超过3 000 m，发动机缸内压力信号高频成分越来越多，对火力面的冲击也越来越频繁，当达到一定频率值时，极有可能对活塞和缸盖造成损伤。

参考文献：

[1] 于宝金,王增全,丁技峰,等.某6V150柴油机变海拔热平衡试验研究[J].车用发动机,2014(5)：71-75.

[2] 陈国金.基于小波分析及ITD法识别气缸内气体压力[J].内燃机工程,2002,23(3):71-75.

[3] Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings Mathematical Physical & Engineering Sciences,1998,454(1971):903-995.

[4] 徐红梅,郝志勇,杨陈,等.基于EMD和HHT的内燃机噪声信号时频特性研究[J].内燃机工程,2008,29(6):60-64.

[5] 杨世锡,胡劲松,吴昭同,等.旋转机械振动信号基于EMD的希尔伯特变换和小波变换时频分析比较[J].中国电机工程学报,2003,23(6):102-107.

[6] Zhaohua W U,Huang N E.Ensemble empirical mode decomposition: a noise-assisted data analysis method[J].Advances in Adaptive Data Analysis,2008,1(1):1-41.

[7] 胡杰,颜伏伍.基于EMD和HHT的内燃机瞬时转速信号分析[J].车用发动机,2010(3):15-19.

[8] 钟佑明,秦树人,汤宝平.一种振动信号新变换法的研究[J].振动工程学报,2002,15(2):233-238.

[9] 卢珍.经验模态分解在信号分离中的应用[D].广州：中山大学,2010.

[10] 关晓磊,颜景龙.爆破振动信号的HHT时频能量谱分析[J].爆炸与冲击,2012,32(5):535-541.