基于车牌识别系统的卡口可达性网络构建

张 杰，王山东，徐志远，刘恒瑞

（1.河海大学地球科学与工程学院，江苏 南京211100）

项目来源：国家自然科学基金资助项目（41271538）。

目前,对交通可达性的研究日益成熟，但现有的交通可达性研究中车牌识别卡口之间的可达性研究较少。本文从交通可达性概念出发，研究车牌识别卡口之间的可达性关系，构建车牌识别卡口可达性网络［1］。

A*算法作为一种启发式算法［2］，在最短路径搜索中有着重要的应用［3］。本文以双向搜索的A*算法为基础［4］，针对在卡口可达性网络构建中遇到的问题对A*算法进行改进，用于计算卡口间的可达关系，构建可达性网络。

1 卡口可达性网络与改进的A*算法

1.1 车牌识别系统

车牌识别系统在城市安全管理中有着重要的作用［5］，为了城市的安全管理，需要在城市重要的卡口装有车牌识别系统。同时，为了节约车牌识别系统的布设成本、避免数据冗余，不可能对所有的流向实施布设监控，实际布设方案的目标是用最少的车牌识别系统获取路网中尽可能完备的交通信息。

对于每一条路段，车牌识别系统可以布设为监控所有驶入或驶出该路段的车辆信息，同时，车牌识别系统可以对道路卡口进行多流向监控，每一个交通治安卡口的多个流向，如十字路口的八个流向均可布设车牌识别系统，如图1所示。因此，车牌识别系统的监控是一种基于流向的监控, 可达性网络为有向图。因此，在进行可达性网络构建之前，需要先确认城市车牌识别系统的布设方案。

1.2 卡口可达性网络

本文将卡口之间的可达关系分为直接可达关系、唯一直接可达关系和非直接可达关系，将可达性网络分为直接可达网络和唯一直接可达网络。

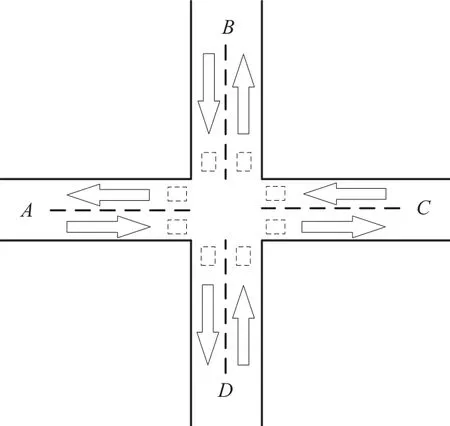
图1 基于流向布设的车牌识别系统

设两个车牌识别卡口为C1、C2，若其间存在一条路径P，使得C1从任意方向能够不通过其他任何卡口到C2，则P称为直接可达路径，称C1、C2存在直接可达关系；若其间有且仅有一条路径P，使得C1从任意方向能够不通过其他任何卡口到C2，则P称为唯一直接可达路径，称C1、C2存在唯一直接可达关系；若其间不存在任何一条路径，使得C1能够不通过其他任何卡口到达C2，则称C1、C2之间为非直接可达关系。

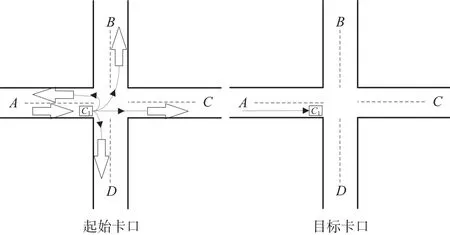
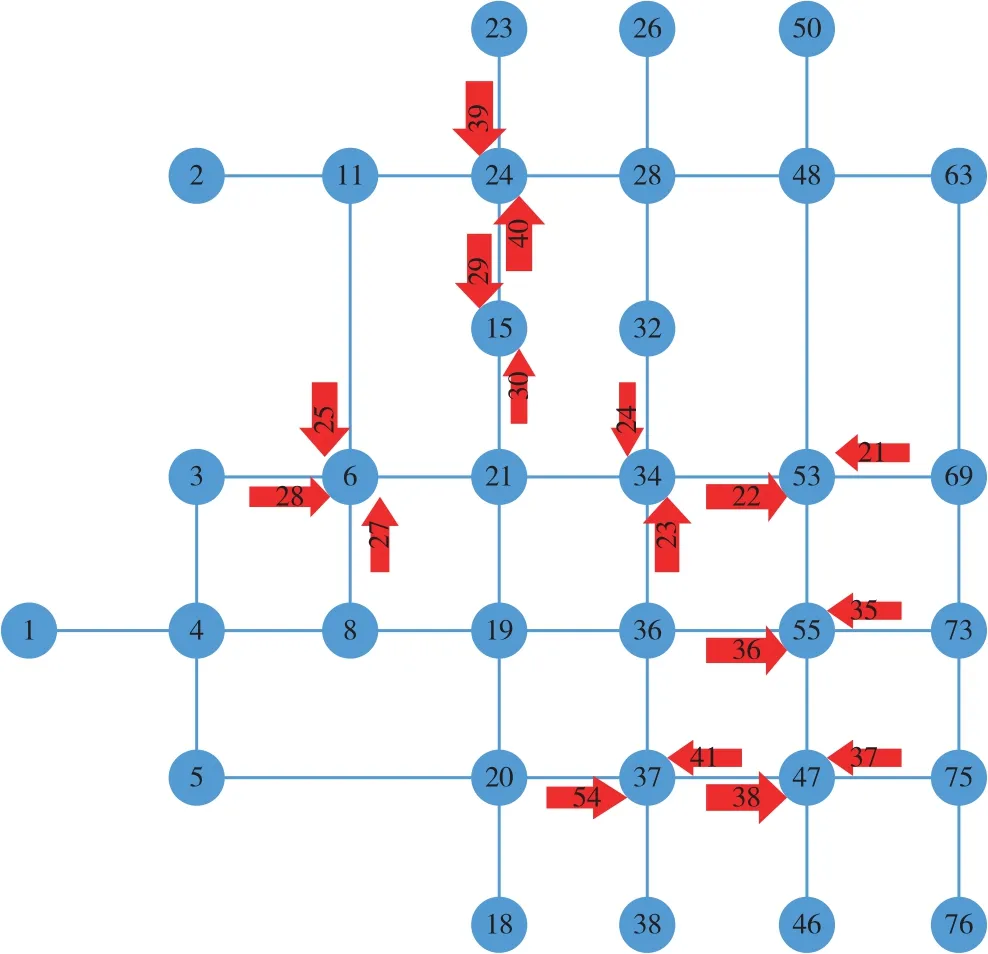
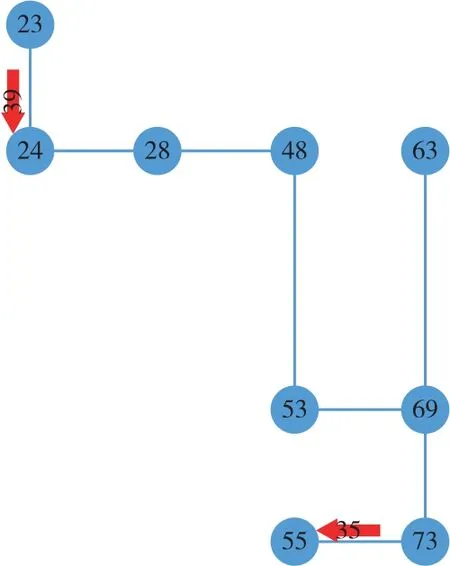
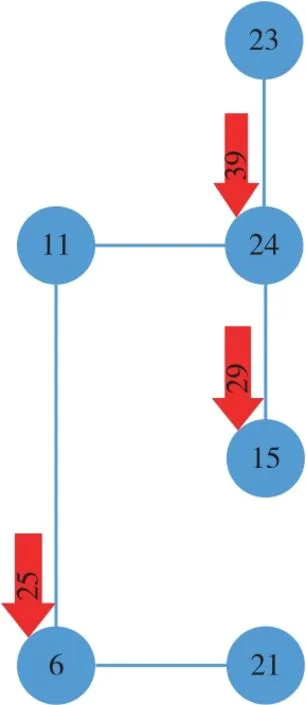
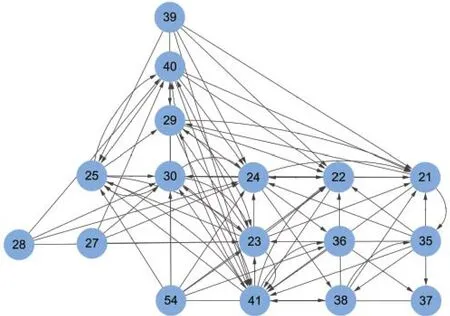
一个有序的二元组

1.3 问题提出

卡口可达性网络构建的核心在于判断两个车牌识别卡口之间的直接可达关系和唯一直接可达关系，即直接可达路径的存在性及唯一性。从本质上看，直接可达路径的求解相当于最短路径问题，在道路网络中确定起点、终点、道路及约束条件，寻找起讫点间符合约束条件的路径，因此两个车牌识别卡口间的直接可达路径可以借助最短路径算法求解。

由于直接可达路径搜索是在两个车牌识别卡口之间进行的，基本元素为卡口边，并非单一的道路结点，所以考虑将最短路径算法中输入和搜索过程中的结点均转换为边的形式。同时，起讫卡口均为具有方向的边，起始卡口监控多个驶出方向，任何一个方向均可能与目标卡口存在直接可达路径，因此计算之前需要根据车道明确起始卡口的驶出方向，而目标卡口的监控方向即为车辆的驶入方向。图2为车牌识别卡口C1分别作为起始卡口和目标卡口时车辆的驶出方向与驶入方向。

图2 起始卡口和目标卡口方向示意图

这样，直接可达路径的求解问题就转变成了以起始卡口及驶出方向为起点、目标卡口为终点，城市道路网络为载体，除起讫卡口外其余所有卡口作为障碍物约束条件下，起始卡口与目标卡口之间的路径规划问题。

1.4 改进的A*算法

由于卡口可达性网络构建的核心是车牌识别卡口之间直接可达路径的存在性，并非严格的最短路径，即计算精度要求不高；但针对所有车牌识别卡口各个可能的驶出方向，均要对其余所有卡口进行直接可达路径的计算，对于复杂的道路网络以及密集布设的车牌识别卡口，计算量仍旧庞大，需要对问题求解的效率进行考虑。

本文采用改进的A*算法为基础，应用到直接可达路径的求解问题中。针对卡口可达性网络构建中遇到的问题对基础算法进行改进，用于计算卡口间的可达关系。算法的改进思想如下：①以图数据结构中的有向边而非结点作为输入元素，采用两条有向边末端端点计算启发式距离；若结点搜索过程中遇到车牌识别卡口边形成的障碍边，则跳过继续运行，即直接可达路径不能经过其他卡口；②由于判断直接可达路径存在性的同时，需要判断路径的数量，即直接可达关系是否为唯一直接可达关系，所以在寻找到目标卡口后将路径存储至路径库，算法继续运行，以开放列表是否为空作为算法的终止条件；③算法结束时若路径库为空，则寻径失败，起讫卡口间为非直接可达关系；若路径库中存在唯一路径，则起讫卡口间为唯一直接可达关系；若路径库中存在多条路径，则起讫卡口间为直接可达但非唯一直接可达关系。

改进的A*算法执行步骤如下：

1）初始化，确定起始卡口S=(i, j)和驶出方向，终点卡口T=(u,v)，将起始卡口加入开放列表并计算代价估值F(S)=G(j)+H(j)，设置父边p(S)为空。

2）边选择，寻找开放列表中代价估计值F最小的有向边C，弹出作为当前边。

3）判断C=T是否成立，若成立，则将寻找到的路径、距离、到达时间等存入路径库，转到步骤7），否则转到步骤4）。

4）将C加入关闭列表，检查C的每条相邻边N，若N在关闭列表中为障碍物边，则跳过；若N不在开放列表中，则转向步骤5）；若N已在开放列表中，则转向步骤6）。

5）将N加入开放列表，并设置父边p(N)=C，计算代价估值F(N)。

6）边松弛，对有向边N进行松弛，即判断G(C)+w(N)

7）若开放列表为空，输出路径库并判断起讫卡口间的可达关系，算法结束，否则转向步骤2）。

2 可达性网络构建实例分析

以马鞍山市道路网络为例，针对每一个车牌识别卡口及可能的行驶方向，分别以其作为起始卡口，将其余卡口分别作为目标卡口，采用改进的A*算法计算两个卡口之间的可达关系；将所有存在直接可达关系和唯一直接可达关系的车牌识别卡口组合，以道路网络中所有车牌识别卡口为结点，以卡口间的可达关系为边，构建卡口的直接可达网络和唯一直接可达网络。图3为马鞍山市道路网络模型及车牌识别系统布设方案，结点代表道路交叉口结点，结点间的连线代表有向路段，箭头代表该流向路段为布设有车牌识别系统的卡口，示例路网中共布设有17个流向的车牌识别系统。

图3 道路网络模型及车牌识别系统布设方案

从图4中可以看出，39号卡口与35号卡口为直接可达关系，且存在多条路径使两个卡口直接可达；39号卡口与25号卡口为唯一直接可达关系，只存在一条路径{23,24,11,6｝使得两个卡口直接可达，如图5所示。

图4 直接可达关系

图5 唯一直接可达关系

车牌识别卡口直接可达网络如图6所示，唯一直接可达网络如图7所示，从中可以看出任意卡口之间的可达关系，如39号卡口是路网的入口点，只能作为可达关系中的起始卡口而无法作为目标卡口。唯一直接可达网络是直接可达网络的子图，存在唯一直接可达关系的卡口之间能够用于重建确定性的车辆轨迹。从图中可以看出，唯一直接可达关系的数量要远小于直接可达关系。

图6 直接可达网络

图7 唯一直接可达网络

3 结 语

本文从交通可达性概念出发研究卡口可达性，将卡口可达性网络分为直接可达性网络和唯一直接可达性网络。对计算最短路径的A*算法进行改进，在城市道路网络和车牌识别系统布设方案的基础上，用于计算卡口间的可达关系，构建城市车牌识别卡口可达性网络，对卡口车辆数据的深度挖掘有一定的意义。

[1] 约翰斯顿 R J． 人文地理学词典[M]．北京: 商务印书馆, 2004

[2] 张海涛, 程荫杭． 基于A*算法的全局路径搜索[J]．微计算机信息,2007,23(17):238-239

[3] 刘浩,鲍远律． A*算法在矢量地图最优路径搜索中的应用[J]．计算机仿真,2008(4):253-257

[4] 孟庆浩,刘大维． 基于双向A*算法的自主车全局路径规划[J]．天津大学学报:自然科学与工程技术版, 1998(6):747-751

[5] 黄健敏．浅谈我国目前车牌识别系统的应用研究[J]．山东工业技术, 2016(1):214-214