光电跟踪转台伺服控制策略研究

吕宏宇,金刚石,刘立志

(1.中国科学院太空应用重点实验室,中国科学院空间应用工程与技术中心,北京100094；2.华北光电技术研究所,北京100015;3.北京新能源汽车股份有限公司，北京 100176)

1 引 言

高性能转台在光电跟踪领域得到了广泛的应用。在这种应用场合,转台需具备连续、稳定、精准跟踪机动目标的能力,因此,在该类转台的设计过程中,伺服控制性能决定着系统目标跟踪精度等一系列关键指标,是一项核心关键技术。

此类转台对控制器的小信号跟踪能力提出了很高的要求,而大转动惯量和高摩擦力矩增加了实现这种性能的难度。大转动惯量导致机械谐振频率较低,高动态响应下易产生机械谐振,无法满足高精度机动跟踪的需求；摩擦力矩是个典型的非线性环节,会恶化跟踪性能,严重降低跟踪精度。传统的双闭环控制已无法满足此类转台的性能需求。

本文针对此类转台的特点,通过项目实践总结了高性能光电跟踪转台伺服控制算法的设计流程。采用复合控制的策略,在反馈控制中增加扰动观测器抑制摩擦等扰动的影响,增加零相位误差跟踪控制器提高转速跟踪能力,采用非线性位置反馈提高反馈效率；在低速率位置给定的情况下进行位置指令细分和速度预测,用于前馈控制。通过项目产品实践表明,以上研究方法可有效提高转台性能,满足实际光电跟踪转台的使用需求。

2 转台数学模型

转台的单轴物理模型如图1所示。

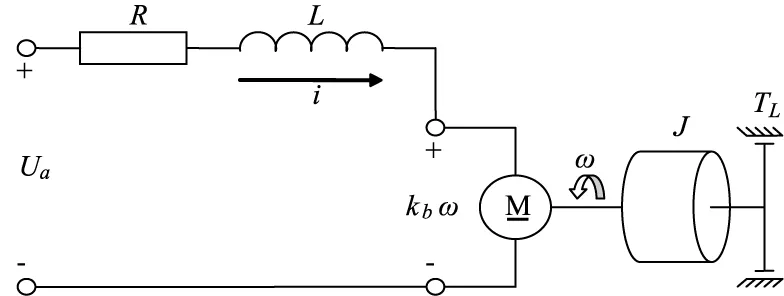
图1 转台单轴物理模型Fig.1 Thephysical model of turntable

可据此建立转台单轴的数学模型[1-3]:

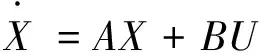
(1)

Y=CX+DU

(2)

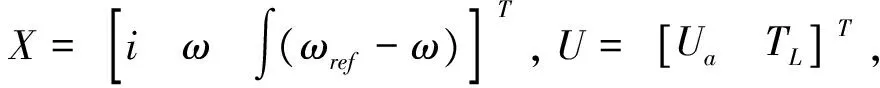
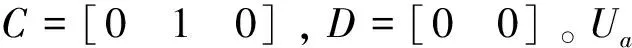
TL=signω·T0+kfω

(3)

其中,T0为摩擦力矩偏置值；kf为摩擦力矩系数。

3 控制算法设计

3.1 LQR转速反馈控制器设计

LQR控制需要根据被控对象的数学模型确定二次型性能指标,据此推导出最优反馈增益,实现预期的性能指标。针对转台数学模型,可以得出系统闭环模型为:

(4)

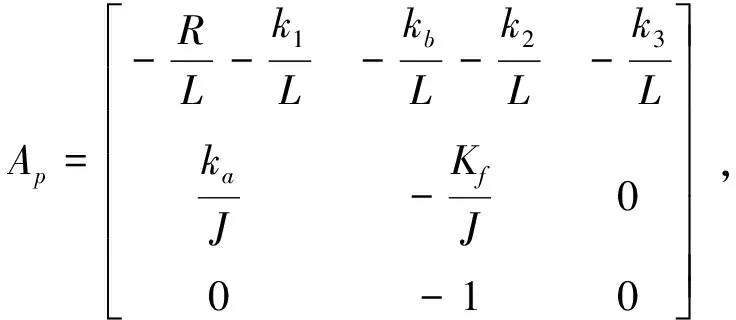
3.2 扰动观测器(DOB)的设计

为抑制摩擦力等扰动对转台控制的影响,并保证实际模型与标称模型的一致性,提高转台控制的鲁棒性,在内环增加了DOB,其原理如图2所示。

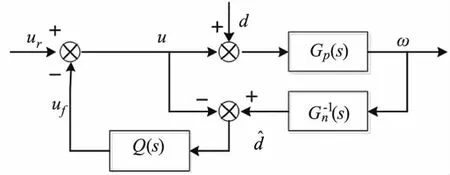
图2 扰动观测器原理框图Fig.2 Block diagram of disturbance observer

DOB的基本思想为将实际转速输入至转台单轴系标称逆模型中,将其输出与实际控制作用比较获得扰动作用的信息,前馈至控制作用以抵消扰动的影响。由于实际转台模型的逆模型无法物理实现,因此加一级滤波器,滤波器的带宽决定了DOB的性能[4-5]。

3.3 ZPETC的设计

在机械谐振频率的限制下,转速闭环带宽一般较低,对正弦的跟踪会存在较大误差,该误差主要是由于相位滞后引起的,ZPETC可以有效地降低此类误差[6]。加入ZPETC后的控制结构如图3所示。

图3 加入ZPETC后的控制结构图Fig.3 The control structure diagram with ZPETC

设转速闭环系统的离散传递函数为:

(5)

式中,z-m为系统m步纯滞后；Bu(z-1)为闭环系统具有不稳定零点和不可对消部分；Ba(z-1)为闭环系统具有稳定零点和可对消部分。则ZPETC的离散传递函数为:

(6)

3.4 前馈控制器设计

前馈控制的框图如图4所示。

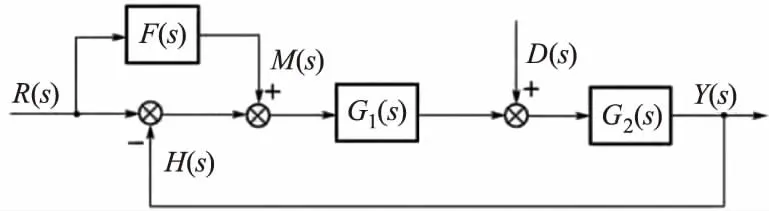
图4 前馈控制结构框图Fig.4 Block diagram of feed-forward control

闭环传递函数为：

(7)

4 控制策略改进及测试结果

4.1 改进后的控制策略

在高精度光电跟踪伺服控制系统中,PID控制等单纯反馈控制算法很难同时满足跟踪定位的高精度、快速性以及对位置的无超调或者小超调,主要原因在于,反馈控制的本质是利用误差来抑制偏差,也就是反馈控制在系统误差建立后才能起作用,其调节的前提条件为存在输出误差并且误差的反馈不会有大的延迟,当被控对象存在延时或者外界扰动,反馈控制的作用很难达到高水平,而前馈控制可以根据实际信号的变化进行调整,利用系统测量的扰动量对系统进行补偿,其扰动噪声和前馈补偿作用几乎同步产生,这样能够弥补反馈控制的不足,基于前馈和反馈的复合控制算法能够同时发挥前馈控制和反馈控制的优点,从而提高伺服控制系统的精度和响应。为了提高机动目标跟踪精度,本文采用复合控制的方式,根据位置给定预测目标运动的速度,前馈至速度环的给定。根据参数辨识得到的转台位置闭环模型,设计零相位误差跟踪控制器,来进一步提高位置环响应带宽和减小位置跟踪误差。

基于以上,本文针对高性能光电跟踪转台的特点,综合考虑扰动干扰以及其他误差因素,控制策略上做了一定的改进和优化,单轴的伺服控制策略如图5所示。

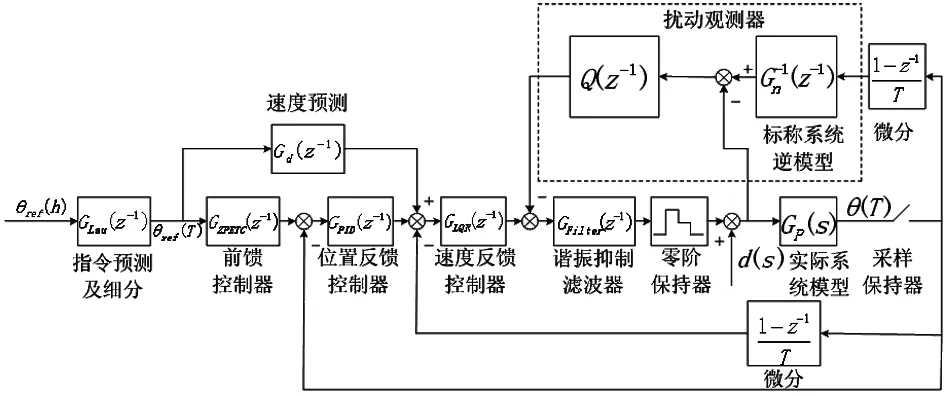
图5 伺服控制策略结构图Fig.5 Structure of servo control strategy

图5所示的单轴伺服控制策略的外环为位置环,位置环控制采用非线性的反馈方式进行优化,与传统控制器采用的线性反馈相比,非线性反馈具有一些非常理想的特性,反馈效率更高。如图6所示,取误差状态的0.5次方值进行反馈可实现大误差低增益控制、小误差高增益控制的特性,可有效地降低超调量、提高稳态精度。

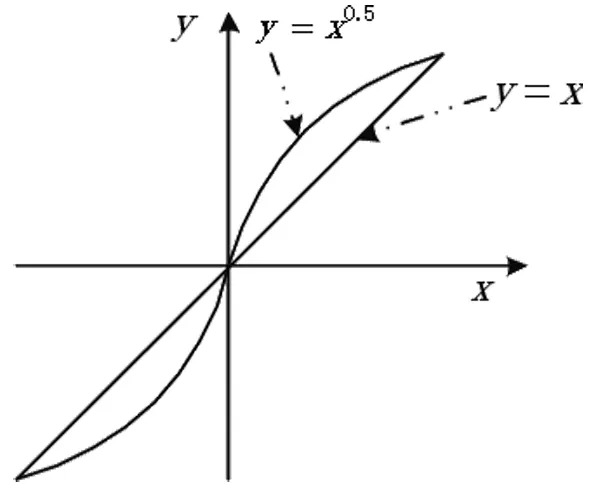
图6 线性反馈与非线性反馈对比Fig.6 Comparison of linear feedback and nonlinear feedback

非线性反馈控制器表达式:

(8)

单轴伺服控制策略的内环为速度环,速度环设计线性二次最优的控制算法。考虑到转台旋转轴的摩擦现象,会引起转台低速跟踪时的滞后、爬行等有害特性,严重降低转台的跟踪精度,因此内环需要根据实测的摩擦模型进行实时补偿。本文采用静摩擦和粘滞模型描述摩擦现象,通过实际测试,得到模型参数,转台实际运行时通过转速信息实时计算出需要补偿的控制量,提高跟踪精度；转台旋转轴参数的时变性、模型的不确定性等扰动也会降低跟踪精度,因此内环采用干扰观测器抑制这些不确定性扰动对转台性能的影响,可提高转台控制的鲁棒性。

当转台工作于图像跟踪工作模式时,位置给定频率较低,通常跟踪器给出的脱靶量信息频率为50 Hz,在进行目标速度预测时会产生较大的量化误差,这会在伺服控制的前项通道中引入延迟,引起跟踪过程中的不平稳,严重影响转台跟踪精度和伺服带宽,本文采用插值细分的方式,将50 Hz的位置给定频率提高至伺服控制频率1 kHz,以减弱延迟的影响,提高性能。在插值细分的同时,也带来了噪声,因此要在细分后加入滤波器,来平滑给定的位置数据,使转台平稳跟踪。本设计中采用式(9)的一阶惯性滤波算法,这种算法是采用本次采样值与上次滤波输出值进行加权,得到有效滤波值,使得输出对输入有反馈作用,可以实现对位置给定数据的滤波处理,在线调整滤波系数Ca值就可以调整滤波程度。

Yn=(1-Ca)·Yin+Ca·Yn-1

(9)

式中,Yn为本次滤波处理的输出值；Yn-1为上一次滤波处理输出值；Yin为需要滤波的位置数据输入。

视频跟踪器送出的脱靶量数据本身由于图像识别和计算处理具有一定的时延,再加上滤波器相位滞后,这个时间延迟形成了较大的跟踪误差,特别是对于高机动性目标。为减小跟踪误差,设计卡尔曼滤波预测技术,减小由于信号滞后形成的系统误差。在目标位置预测的同时,预测算法也可以获取预测估计的目标速度信息和加速度信息。以此信号构建速度前馈,可以有效减小速度跟踪误差,也可有效提高跟踪精度。

改进后整体控制策略设计框图如图7所示,图5所示的伺服控制策略包含在整体的控制策略之中。

图7 改进后整体控制策略框图Fig.7 Improved block diagram of overall control strategy

4.2 综合试验测试结果

图8为位置给定输入曲线、速度曲线和控制策略改进前的跟踪误差曲线。位置给定输入为

θ=Asin(ωt)=Asin(2πft)

(10)

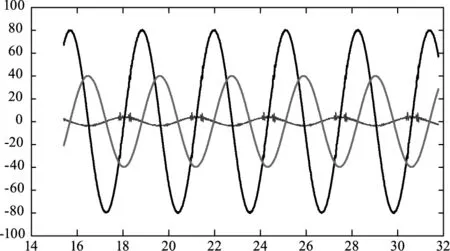
图8 位置给定及跟踪误差曲线图Fig.8 Location reference and tracking error curve

在没有进一步优化的LQR转速控制器正弦跟踪效果如图9所示,波形分别为转速的给定、反馈和跟踪误差。由于摩擦力的影响,导致转速过零点的误差较大,需要设计补偿算法来减小跟踪误差。

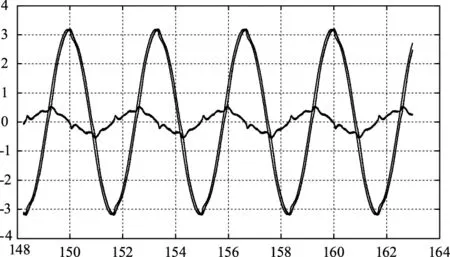
图9 转速环正弦跟踪曲线图Fig.9 Sinusoidal tracking curve of speed ring

下面从位置给定输入进行测试,图10中方波曲线是50 Hz的位置输入,图中上面两条曲线为插值预测曲线,为了补偿插值后滤波的延迟,在插值时提前了两个时间周期,最上侧曲线是拉格朗日插值后的位置曲线,中间曲线为经过一阶惯性滤波后位置给定值,横坐标为采样时间点,每个点为2 ms,纵坐标为位置角度值。可以看出经过插值滤波后的曲线和给定曲线在50 Hz频率上有位置重合。

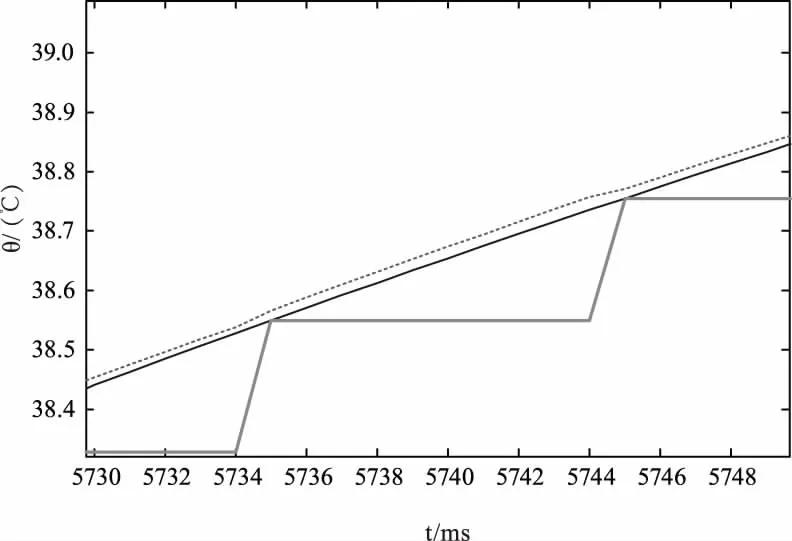
图10 位置给定插值前后曲线图Fig.10 Positionreference before and after interpolation

在实际目标跟踪测试时,视频跟踪器实时提取实际靶标目标的特征,给出更新率为50 Hz的脱靶量数据,控制器采用复合控制方式,利用常增益的卡尔曼预测滤波器预测速度值,并结合高增益微分器进行估计速度。图11中带有毛刺噪声的曲线是由位置给定计算的原始速度,另外两条曲线分别是利用卡尔曼滤波预测的速度曲线和利用二阶线性高增益微分器估计的速度曲线,图中对比可以看出,不经过滤波预测的速度有很大的噪声,毛刺部分的加速度接近于无穷大,直接作为给定的话会使速度环不稳定。利用卡尔曼滤波预测的速度和二阶线性高增益微分器估计的速度没有太大的速度突变,比较适合参与速度环运算,而这两种预测对比之下,卡尔曼滤波预测较二阶高增益微分器有一定的延迟,但是适应性要更强些。

图11 原始速度与两种预测速度曲线对比图Fig.11 Comparison of original speed and prediction speed curves

进一步测试采用零相位误差跟踪控制器,可以大幅提高转速跟踪精度,如图12、图13所示。

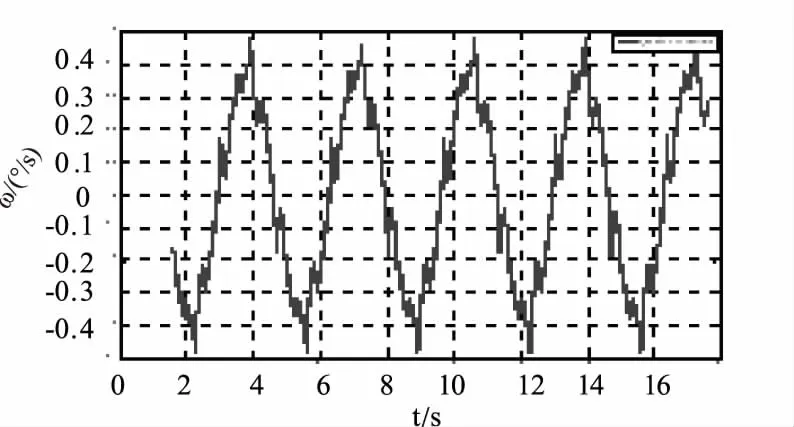
图12 未加ZPETC时的转速误差Fig.12 Speed error curve without ZPETC

图13 加入ZPETC后的转速误差Fig.13 Speed error curve with ZPETC

使用改进后的整体控制策略,在目标加速、匀速、反向加速运动的整个过程中,转台可以始终稳定地将目标锁定于视场中心,稳态时的跟踪误差及其统计值如图14所示,误差的STD值可以到0.0033。

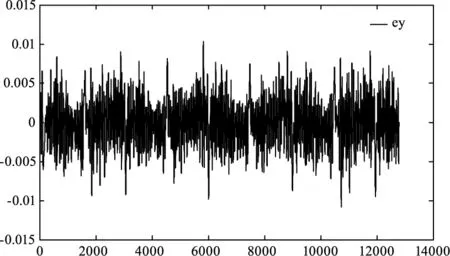
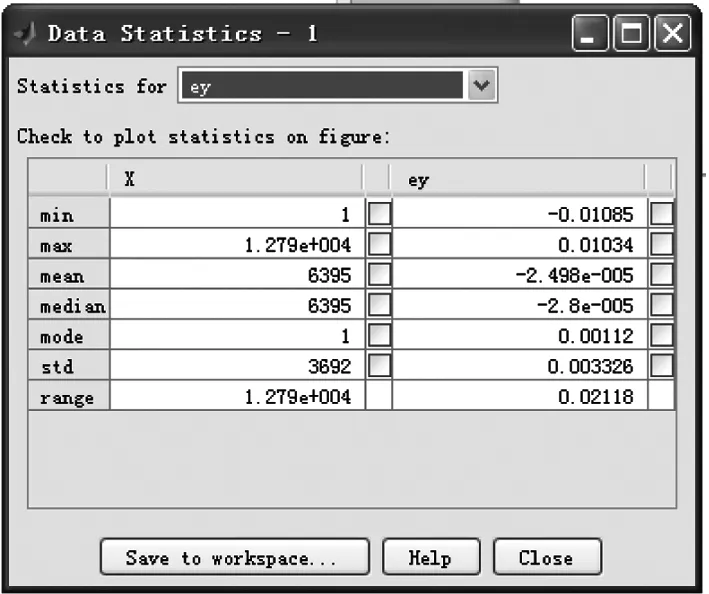
图14 实际目标跟踪误差及其统计值Fig.14 Actual target tracking error curve and its statistical value

5 总 结

本文总结了高性能光电跟踪转台伺服控制算法的设计过程,从给定指令处理、反馈控制和前馈控制三个方面阐述了各种控制策略的实现过程,并给出了相应实际应用中采集测量的曲线波形,试验表明,本文控制策略对提高速度环的动态响应有很好的改善,对目标跟踪特别是大角加速度跟踪情况下的跟踪精度有显著提高,验证了控制策略的有效性和设计合理性,总体指标满足了实际应用需求,对其他项目的高性能跟踪转台设计及相关伺服控制系统设计具有借鉴意义。

参考文献：

[1] JIN Gangshi,et al.Design of the DC motor controller based on modern control theory[J].Laser & Infrared,2009,39(10):1082-1085.(in Chinese)

金刚石,等,基于现代控制理论的直流电机控制器的设计[J].激光与红外,2009,39(10):1082-1085.

[2] YANG Tianxi.Several control algorithms of optical testing simulator [D].Harbin:Harbin Institute of Technology,2007.(in Chinese)

杨天锡.光学测试转台若干控制算法研究[D].哈尔滨：哈尔滨工业大学,2007.

[3] ZHANG Ping.Modeling and control of airborne/missile-borne vision-guidance stabilized platform[M].Beijing:National Defence Industry Press,2011.(in Chinese)

张平,机载/弹载视觉导引稳定平台的建模与控制[M].北京：国防工业出版社,2011.

[4] WANG Xinhua,LIU Jinkun.Differentiator design and application[M].Beijing:Publishing House of Electronics Industry,2010.(in Chinese)

王新华,刘金琨.微分器设计与应用[M].北京：电子工业出版社,2010.

[5] WANG Guoqing.Researching on adaptive tracking filter algorithm and its implementation method[D].Xi′an:Xidian University,2007.(in Chinese)

王国庆.自适应跟踪滤波算法研究及其工程实现[D].西安：西安电子科技大学,2007.

[6] ZHANG Houlai.Direct current servo controller design for engraving machine based on zero phase error tracking control[J].Micromotors,2012,45(6):61-64.(in Chinese)

张后来.基于ZPETC的雕刻机直流伺服控制系统设计[J].微电机,2012,45(6):61-64.