基于激光脉宽精确控制获得准直高能电子束的研究

南京邮电大学理学院 郅佳琳 肖耀宗

南京邮电大学贝尔英才学院 王子豪

南京邮电大学理学院 田友伟

1 引言

新型超强超短脉冲激光的出现与发展，为人类提供了前所未有的全新实验段与极端的物理条件。特别是啁啾放大技术[1]的进步使得激光脉冲聚焦到远超过1018Wμm2/ cm2成为可能，在实验和理论上拓展了粒子加速的研究方式。高强度的激光脉冲也打开了相对论层面光与物质相互作用的大门[2]，在医学、超精细微加工、高密度信息储存等领域有很好的发展前景，如人工引雷，快速点火，超高次谐波的产生、粒子加速等[3]。本文研究对紧聚焦的高斯激光脉冲精确控制以获取准直高能电子束的问题。众所周知，平面波脉冲不能加速电子[4]，这是由于在平面波脉冲的作用下，虽然脉冲的上升沿加速电子使其获得了很大的能量，但电子在脉冲的下降沿会被减速，加速和减速作用相互抵消。导致光脉冲和电子分离以后，电子没有获得能量增益。Hartemann等人提出了非线性有质动力散射电子使其加速从而抽离电子的想法，电子加速的关键性问题就是从激光束抽离备加速的电子。本文主要讨论真空中紧聚焦激光与初始状态静止在激光传播轴上的电子的相互作用，当激光强度a0和激光束腰半径b0给定时（a0= 6，b0= 3λ0），通过改变激光脉宽L来观察激光与电子相互作用后电子的速度偏角和其能量增益的变化规律，以获得准直性好的高能电子束。

2 电子加速模型与基本方程组

紧聚焦线偏振高斯型脉冲激光场归一化矢势通常写成下面的形式：

在直角坐标系中，光场的矢势可以写成：

其中：

实际上，当光脉冲的束腰半径大于5λ0时，az比ax，ay小一个数量级。电磁场中单个电子的运动状态洛伦兹方程以及电子的能量方程如(4) 、(5)所示：

其中μ是用光速c归一化的电子速度，a是用mc2/ e归一化的矢势，P = γu是用mc归一化的电子动量，是相对论因子，也是用mc2归一化的电子能量。方程（4）的只作用于a上。

将(2)代入(4)和(5)方程进行代换得到如下方程组

其中ux，uy，uz是电子在x，y，z方向上的速度分量。求解方程(6-9)，可以得到电子在激光场中的运动轨迹以及能量随时间的变化过程。

图1 激光参数为a0 = 6, b0 = 3λ0 L=1λ0时电子运动轨迹图（上）和电子能量增益图（下）

3 结果讨论

当参数a0，b0给定时，对于初始静止在激光传播轴上的电子，激光脉冲宽度值对其运动轨迹有很大的影响。图1是激光脉宽为L=1λ0（λ0是用归一化后的波长）的线偏振高斯脉冲作用时，电子的运动轨迹图与能量增益图。从轨迹图可以看出，电子在传播方向上平移了大约0.5倍瑞利距离时明显偏离传播轴，由于电子在轴上平移的距离远小于光脉冲的瑞利长度[5]，因此这样的光脉冲和电子相互作用时，脉冲束腰半径的变化完全可以忽略不计。在此过程中，电子在脉冲上升沿被加速到最大能量15，在激光下降沿被减速，脱离激光束后电子。这是由于电子纵向移动的距离远远小于瑞利长度，径向运动的最大半径远远小于束腰半径，在激光和电子整个的作用过程中激光场近似为平面波脉冲，故电子能量增益为0是合理的。

图2中当激光脉冲宽度增大时，激光与电子的作用会发生很大的变化。我们可以看出电子开始有明显的能量增益，且与激光脉宽成正比，这是由于电子在激光传播方向上移动的距离可以和瑞利长度相互比较的结果。

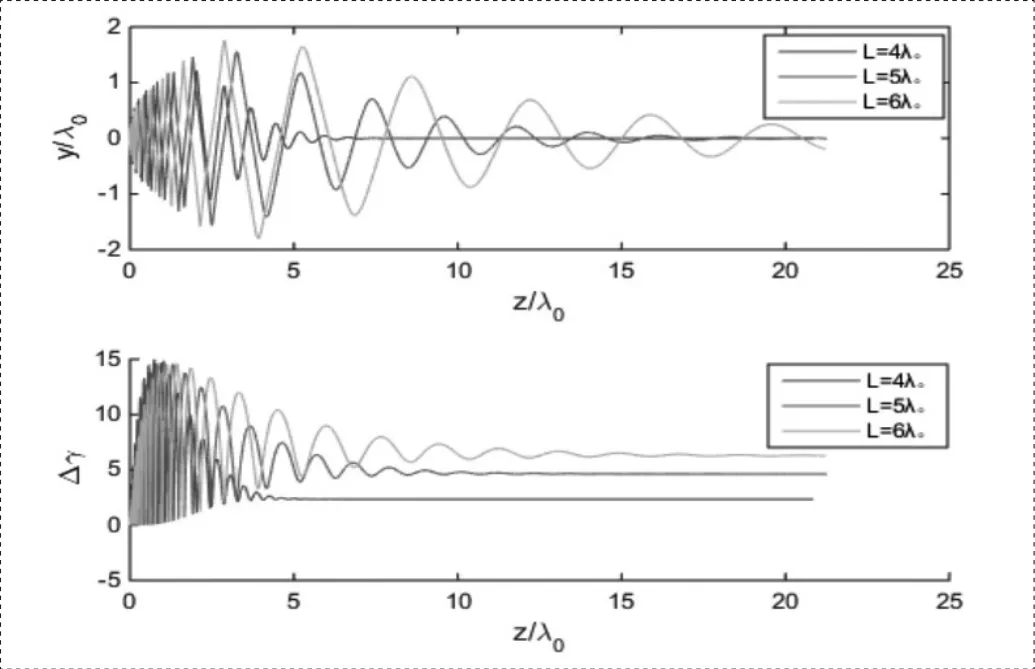
图2 激光参数为a0 = 6, b0 = 3λ0 L=4,5,6λ0时电子运动轨迹图（上）和电子能量增益图（下）

接下来对“准直”和“高能”这两个条件进行研究，我们用matlab编程计算出电子脱离激光脉冲后的能量增益Δγ和速度偏角θ，对数据进行分析归纳出可以获取准直高能电子束所对应的激光脉宽范围。

先对能量增益进行讨论。对激光脉冲L从1λ0到20λ0等距取值，绘制出电子Δγ — L曲线图如图3所示，当激光脉冲宽度在1λ0到10λ0之间时，Δγ 随L的增大明显增加；当L大于10λ0时，Δγ 随L的增大而减小。

图3 电子能量增益变化图（L步长1λ0）

为了进一步精确电子能量增益最大时对应的激光脉宽范围，我们以0.1λ0步长对激光脉宽从8λ0到10λ0之间依次取值，MATLAB计算出对应的Δγ ，根据最终计算数据得到当激光脉宽L为9.1λ0，9.2λ0时，电子Δγ 达到最大为7.635，且在8.6λ0到10λ0区间Δγ 均在7.6左右，能量增益明显。

接下来我们讨论准直性的条件。即计算出电子脱离激光束后的速度偏向角θ，找出θ值较小时对应的激光脉宽参数范围。图4是L在1λ0到20λ0区间的L — θ曲线图，可以看到激光脉宽为1λ0时的电子速度偏角远远大于平均水平，不利于获取准直电子，故此情况下不适用。

图4 电子速度偏角随激光脉宽变化图（L步长1λ0）

为了进一步找出准直性好的加速电子对应的激光脉宽参数值，我们舍掉偏角较大激光脉宽取值，在[3λ0, 10λ0]脉宽区间以0.1λ0为步长，计算得到70组θ数据绘制折线图如图5所示。结合之前的计算结果得到，当L在[1λ0,3.8λ0]区间时θ较大，以[1λ0,2λ0]区间最为明显，不利于获取电子运动轨迹实现捕获；当L在[3.8λ0,9.6λ0]时θ均不超过0.001度，即电子准直性较好；当激光脉宽L>9.6λ0时θ开始增大，电子越来越偏离激光传播方向，电子束准直性越来越差。

综上所述，我们在激光脉宽值L为[8.4λ0,9.6λ0]区间对紧聚焦的激光脉冲进行精确调控就可以获取准直性好的高能电子束。

图5 电子速度偏角随激光脉宽变化图（L步长0.1λ0）

4 结论

本文研究了紧聚焦线偏振激光脉冲与初始静止在激光传播轴的电子相互作用，获取准直高能电子束的激光脉宽的取值范围。通过对相对论电子被激光脉冲作用后的速度偏角以及能量增益情况分析，得到在激光脉宽[8λ0,10λ0]区间存在能量增益的极大值使能量增益达到GeV量级。在激光脉宽大于10λ0时，脉宽对电子的能量增益影响不大。而且在激光脉宽[3.8λ0,9.6λ0]区间电子准直性均较好。综合考虑满足准直、高能两个条件确定出激光脉宽范围。与此同时获取准直高能电子束的研究对电子的反探测也提供了依据，这具有非常重要的实验价值。

本文建立在江苏省国家级大学生创新创业项目课题：基于激光脉冲精确控制获得准直高能电子束的研究的大背景下开展，对影响激光脉冲加速电子其中一个因素即激光脉宽进行研究得出影响结论。

[1]黄颖．啁啾激光等离子体相互作用加速电子模拟研究[D]．东北石油大学,2016．

[2]王乃彦,沈百飞,陆元荣．超强光场驱动的高性能高能粒子束的产生及其应用开拓研究[J]．科技资讯,2016,14(19)∶178．

[3]孙书营,黄永盛,汤秀章．激光加速电子研究进展及其在空间环境模拟中的应用前景[J]．航天器环境工程,2015,32(03)∶318-323．