基于DCQGA的PID参数自整定

江鸿潮，白国振

(上海理工大学 机械工程学院，上海 200093)

PID控制器参数优化的关键问题，是如何获得偏差的比例、积分、微分三者之间的最佳组合。PID参数整定的方法很多，比如常规的Ziegler-Nichol法[1]和Cohen-Coon法等，然而常规方法在实际工程应用中需要依赖很强的实践经验，且不易得到理想的结果。近年来，智能算法在PID控制中的成功应用和发展为PID参数整定提供了新的路径，如人工免疫整定[2]、蚁群算法整定[3]、鱼群算法整定[4]、佳点遗传算法集整定[5]等，这些智能PID整定方法，大幅提高了PID控制系统的控制性能。

在用于PID参数整定的各智能算法中，遗传算法[6]GA(genetic algorithm)便是其中最常用的算法之一，由于GA仅用目标函数在概率准则引导下进行全局自适应搜索,能够处理传统优化方法难以解决的复杂问题,具有极高鲁棒性和广泛适用性,因而在各个优化领域得到了广泛应用.但是GA在实际应用中存在迭代次数多、收敛速度慢、易陷入局部极值和过早收敛等缺陷和不足。

为解决这些问题，Narayanan[7]和Han Kuk-Hyun[8]等将量子计算中的量子比特(qubit)、量子态叠加和量子干涉等概念引入遗传算法，提出了一种新的遗传算法——量子遗传算法(QGA)，该算法使用量子比特进行基因编码，用量子门进行染色体更新，有效地解决了GA中存在的染色体丢失和过早收敛的问题[9]。但QGA的旋转角大小和方向的确定过于复杂，对于多参数函数优化问题容易出现早熟现象[10]。标准QGA由于需要反复查表，计算量大，非常耗时,不便于工程实际应用。

针对以上问题，本文采用一种基于实数编码的双链量子遗传算法[11-12](DCQGA)来整定PID参数。该算法在基本量子遗传算法的基础上进行改进，对转角方向的确定，给出了一种全新的但简单实用的确定方法；对转角迭代步长的确定，构造出1个包含目标函数的梯度信息的转角函数；此外，把量子比特的2个概率幅值都看做基因位，使得每条染色体带有2条基因链，加快了搜索速度。通过与GA和QGA的比较，结果验证了DCQGA在PID参数优化中的优越性。

1 量子遗传算法简述[13]

量子遗传算法是将量子计算原理中的量子态、量子态叠加、幺正变换等引入普通遗传算法而得到的一种新的优化算法，其既具有普通遗传算法优胜劣汰不断进化的优势，又具有量子计算中强大的并行搜索优势。QGA仅用1条染色体就可以同时表示多个状态，而 GA的1条染色体只能表示一种状态，这使得QGA较传统GA具有更好的种群多样性和更高的计算并行性。相较于GA的选择、交叉和变异操作，QGA在染色体更新时采用了量子旋转门操作，大幅地提高了算法的收敛速度。

1.1 量子比特编码

量子比特编码不同于遗传算法中的二进制编码，它的染色体基因位不再用确定的值表示，而是用量子位表示，量子位的值通过随机的方式取得，是一种概率表示形式。遗传算法采用经典比特来表征不同的信息，每个基因位要么是“0”，要么是“1”，是确定的值，它的编码方式属于确定论的范畴；而QGA采用的是量子比特|φ>来表征信息，其中：

|φ>=α|0>+β|1>

(1)

|α|2+|β|2=1

(2)

它的基因位不再是确定的数值，而是量子位|φ>,它是1个不确定的值，它的编码方式属于概率论的范畴，只有人为地去观测时才能得到它的确定值(坍缩为基本态)。就像薛定谔的猫一样，在没有打开箱子时，它是处于既死又活的叠加态，只有打开箱子才能确定猫是处于死态还是活态。

同理，量子比特也有2个基本态|0>态和|1>态，未被观察时量子比特处于两种状态的线性叠加态，一旦有人为的观察时就会坍缩到基本态|0>态或|1>态。其中|α|2给出了量子比特被观察时坍缩到|0>态的概率，|β|2给出了量子比特被观察时坍缩到|1>态的概率。这样，用量子比特编码的染色体不再表示一种单一的状态，而是表示多个状态的叠加。如用n个量子位就可以表示2n个状态。采用多量子比特编码m个参数的基因如下[14]：

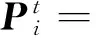
(3)

采用量子比特编码，1条染色体就可以同时表达多个态的叠加，使得QGA比普通遗传算法拥有更好的多样性特征。这样QGA相比传统的GA可以大量减少种群规模，大量地减少计算时间。同时QGA通用性好，且实现简单。

1.2 量子旋转门更新

QGA中染色体的更新是通过量子门来实现的，而量子旋转门是用得最多的一种量子门，它通过对量子比特实施幺正变换来控制量子态的演化和传递，进而实现种群的进化，其更新过程如下[15]：

(4)

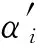
2 基于DCQGA的PID参数整定

PID参数整定是多目标优化问题。首先给出连续优化问题的一般描述[16]：

约束条件为n维空间，其有界闭集Ω中每个点都看成优化问题的近似解，为反映这些近似解的优劣程度，可定义适应度函数：

fit(x)=Cmax-f(x)

(6)

式中：Cmax——给定的1个适度值或目前为止的最大值。

2.1 实数双链编码方案

本文采用的DCQGA中，对编码方案进行了改进[16]：

(7)

式中：Pi——每一代中第i个个体的染色体；θij=2π×rand；rand为[0,1]之间随机数；i=1,2,…,m;j=1,2,…,n；m——种群规模；n——量子位数。

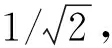
(8)

式中：Pic——余弦解；Pis——正弦解。

2.2 解空间变换

由2.1节的分析可知，无论是QGA还是DCQGA，通过染色体解码得到的值与实际优化问题的解空间都不一致，所以需要进行解空间变换。变换公式如下：

(9)

(10)

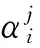
2.3 改进的种群进化策略

2.1节给出了对QGA编码方式的改进，下面对种群进化策略进行改进，DCQGA的种群进化策略同样运用量子旋转门，但在转角方向和大小的确定上都给出了改进措施。

2.3.1量子旋转门的转角方向的确定

DCQGA的量子旋转门为

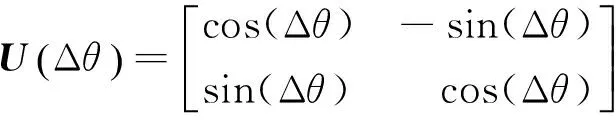
(11)

该量子旋转门不改变量子位的长度，只改变量子位的相位。其更新过程为

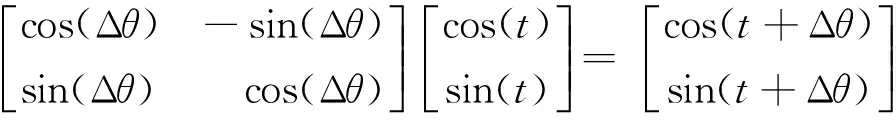
(12)

转角Δθ的大小和方向直接关系到算法的速度和效率。确定转角Δθ的方向，QGA的做法是构造1个查询表[14]，虽然直观但异常繁琐，而且需要频繁地查表，使得QGA的效率偏低。为了简化，DCQGA给出了以下确定转角方向的策略： 令

(13)

当A≠0时，Δθ方向为-sgn(A)；当A=0时，方向取正负均可。其中，α0和β0是当前搜索到的全局最优解中某量子位的概率幅，α1和β1是当前解中相应量子位的概率幅。

证明： 记量子位[α0,β0]T和[α1,β1]T在单位圆中的幅角分别为θ0和θ1，则

(14)

当A≠0时，若0<|θ1-θ0|<π，sgn(Δθ)=-sgn(θ1-θ0)=-sgn(sin(θ1-θ0))=-sgn(A);若π<|θ1-θ0|<2π,则sgn(Δθ)=sgn(θ1-θ0) =-sgn(sin(θ1-θ0))= -sgn(A)。当A=0时，由sin(θ1-θ0)=0，得θ1=θ0或|θ1-θ0|=π，此时，正、反向旋转没有区别，效果相同，故sgn(Δθ)取正负均可。(证毕)

2.3.2量子旋转门转角大小的确定

量子旋转门转角大小的确定一般是构造1个查询表，如文献[14]，旋转幅度大多是根据经验给出，如文献[7]给出了开区间(0.005π，0.100π)的范围，但是并没有给出选择的具体依据。文献[17]给出了一种转角的迭代步长单调下降的调整策略，是一种以进化代数为自变量的负指数函数的自适应调整策略。现有文献大多没有考虑种群中各染色体之间的差异，也没有充分利用目标函数的变化趋势。本文的改进策略是： 把目标函数在搜索点(单个染色体)处的变化趋势(梯度)加入到转角步长函数中，让转角步长的大小随着目标函数变化率增大而减小，反之亦然。这样，既可以加快搜索速度，又不至于越过全局最优解。考虑可微目标函数的变化率，利用梯度定义转角步长函数为

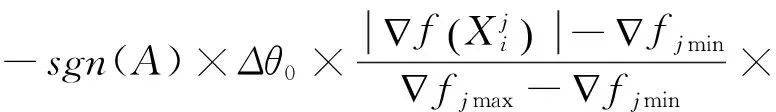
exp(-gen/maxgen)

(15)

式中：Δθ0——迭代初值；gen——当前代数，maxgen为终止代数；适应度函数f(X)在处的梯度；fjmax，fjmin分别定义为

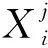
(18)

式中：Xp,Xc——父代和子代染色体。

2.4 变异处理

除了对编码方式以及转角方向和大小进行改进外，DCQGA在基本QGA基础上加入了变异处理。首先依据实际确定的变异概率随机选择需要变异的若干染色体，然后再用量子非门对随机选中的量子位施加变换，使该量子位的4个概率幅互换。这样可使2条基因链同时得到变异。

比如，假设某量子位幅角为θ，则变异后幅角变为π/2-θ,也就是说幅角正向旋转了π/2-2θ。实际上该种变异是对量子位幅角的一种旋转： 该旋转不与当前最佳染色体比较，一律正向旋转，有助于增加种群的多样性，降低早熟的概率。

2.5 DCQGA的算法流程

实现上述实数双链编码梯度QGA的步骤如图1所示。

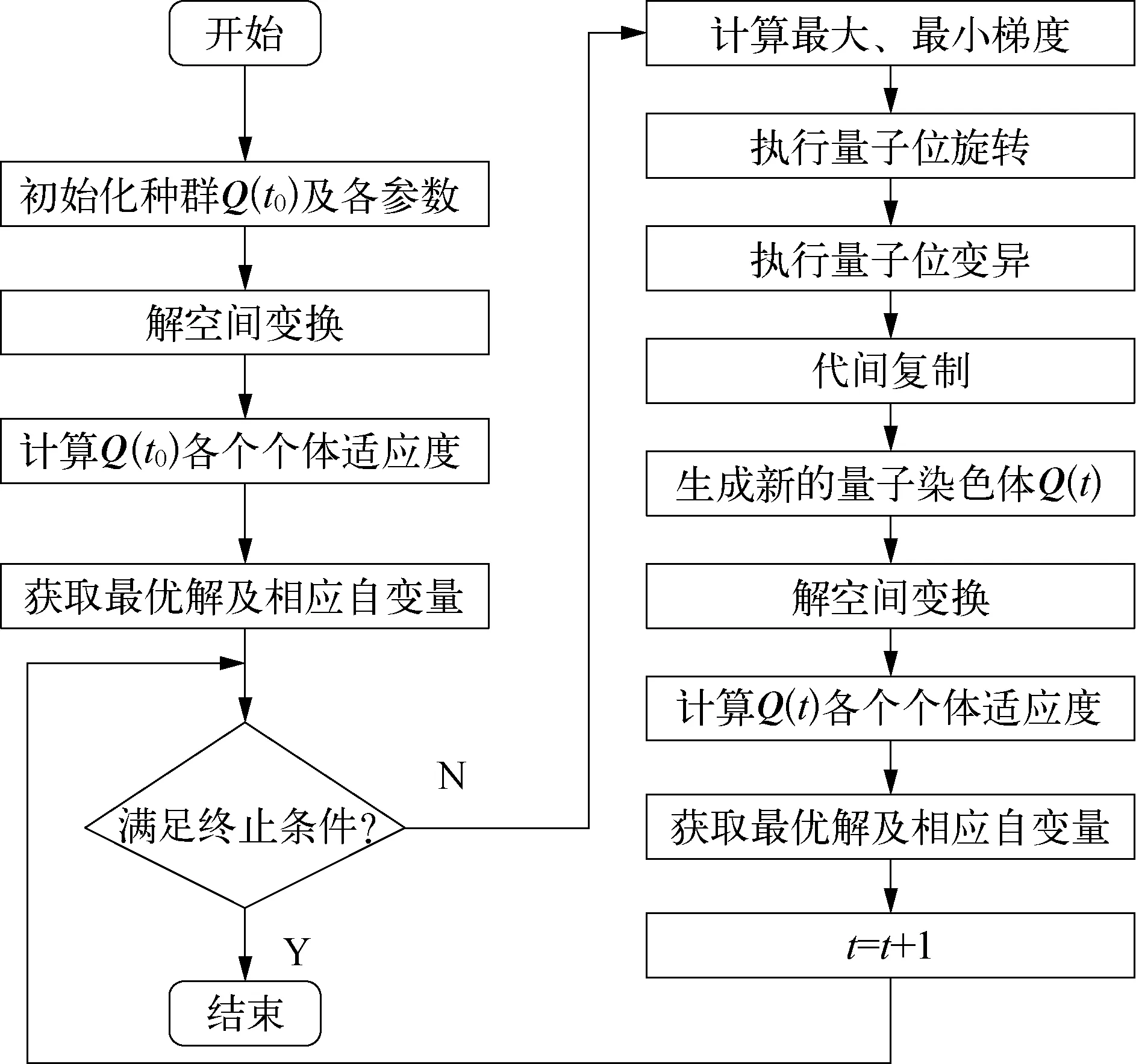
图1 DCQGA流程示意

1) 种群初始化。按式(7)产生m条染色体(2m条基因链)组成初始种群Q(t0)；设定初始转角步长θ0、变异概率为pm。

2) 解空间变换。将每条染色体代表的近似解，由单位空间In=[-1,1]n映射到连续优化问题式(5)的解空间Ω。

3) 计算初始种群Q(t0)的适应度。按式(6)计算染色体的适应度fit。

4) 获取最优解及相应自变量。记当代最优解为bestX,对应染色体为bestChrome，到目前为止的最优解为BsX，对应染色体为BsChrome。若fit(bestX)>fit(BsX),则BsChrome=bestChrome。

5) 判断是否满足终止条件。终止条件的设定一般有两种： 适应度值达到要求时终止程序；达到指定代数时终止程序，本文采用后者。当满足终止条件时，6)之后的步骤不执行，而不满足终止条件时，进入下一步的循环体。

6) 计算最大最小梯度。根据式(16)和式(17)计算最大最小梯度fjmax，fjmin。

7) 执行量子位旋转。根据式(15)执行量子位旋转,旋转后得到1个关于转角步长Δθ的矩阵。

8) 执行量子位变异。依据变异概率对要变异的量子位实行变异操作： Δθij=0.5π-θij。

9) 代间复制。因为要用到相邻两代的一阶差分替代梯度，所以要先把本代染色体复制上一代，即令oldchrome=chrome。

10) 生成新的量子染色体。由步骤8)得到更新后的Δθij，chrome=cos(Δθij)或chrome=sin(Δθij)得到新的量子染色体。

11) 得到新的染色体后，反复执行步骤2)～5)，直到t达到指定代数时结束。

4 仿真验证

为了验证DCQGA对PID控制器参数优化的有效性，选择如下被控对象[18]：

(21)

令输入为一阶跃信号，采样时间取为1 ms。为了获得满意的过渡过程动态特性，采用误差绝对值时间积分性能指标作为参数选择的最小目标函数。另外，把控制量的平方也加入到目标函数中，这样可以避免控制能量过大，如下式：

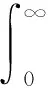
(22)

式中：e(t)——系统误差；u(t)——控制器输出；tu——上升时间；ω1，ω2，ω3——权值。

为避免超调，采用惩罚机制，即一旦产生超调，将超调量也加入目标函数中，即：

ife(t)<0

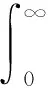
(23)

式中：ω4——权值，且ω4≥ω1。

在用PID控制器对该模型进行控制时，为优化PID控制器参数，各算法参数选择如下：kP的取值范围为[0,20]；kI,kD的取值范围为[0,1]；取ω1=0.999，ω2=0.001，ω3=2.0，ω4=100；限定代数为160代。GA，QGA和DCQGA三种算法针对以上的参数取值均一致。

另外，DCQGA的种群规模取为10，量子位数为3，转角步长为0.002π，变异概率为0.05；GA的交叉概率取为0.9，变异概率为0.033；而QGA的种群规模取为40。

5 结果分析

经过160代的优化，三种算法得到的最优结果见表1所列。

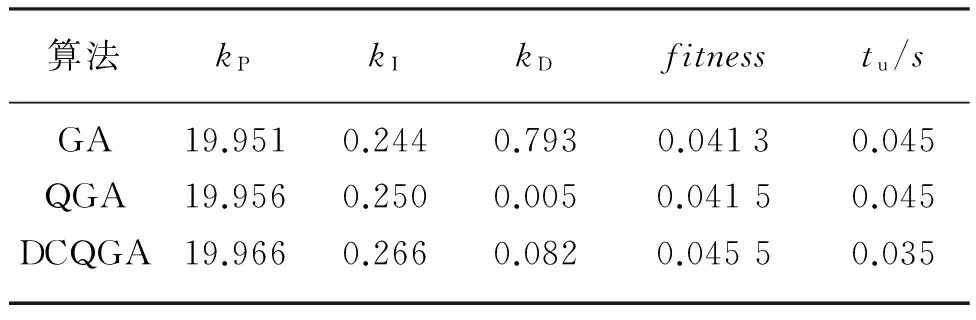
表1 GA，QGA，DCQGA算法结果比较

表1中，fitness表示最优适应度值，tu表示对应算法的上升时间。由表1可知DCQGA的bestfit最大，同时从适应度函数变化曲线图2中也可以看出DCQGA的曲线明显高于另外2条，表明DCQGA可以更快地跳出局部最优解，获得更好的全局最优解，优化结果更准确。

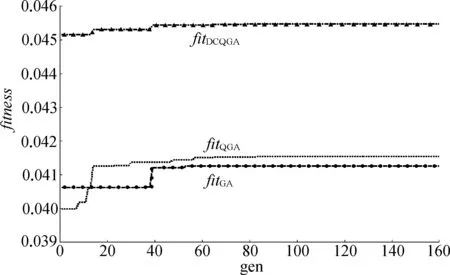
图2 适应度函数变化曲线

图3为DCQGA与QGA和GA优化的PID控制器的阶跃响应的比较。从图3和表1可以看出DCQGA得到的曲线上升时间最快，上升时间tu最小，说明DCQGA的响应速度最好。

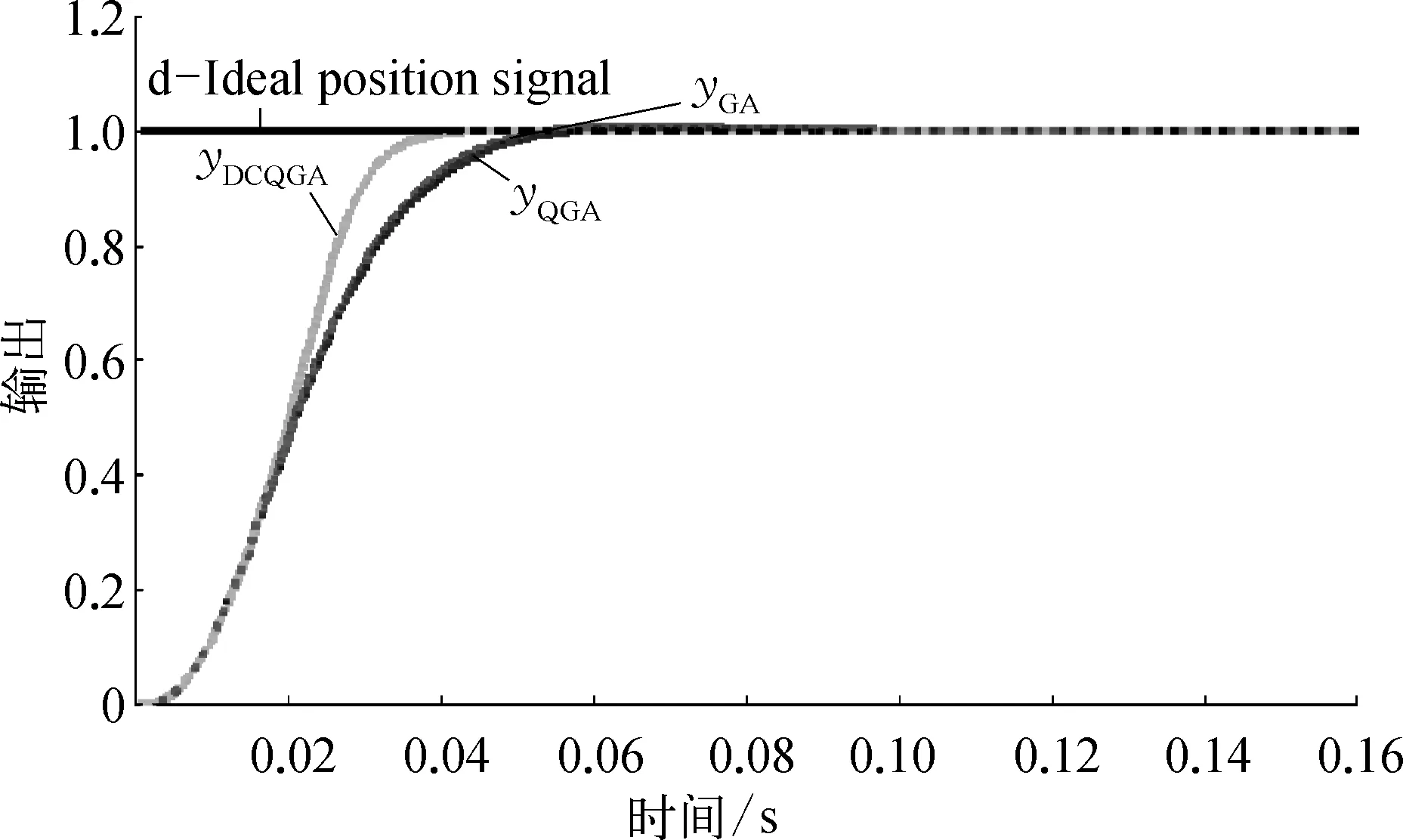
图3 PID控制器的阶跃响应示意

6 结 论

本文提出一种基于实数编码的双链量子遗传算法的PID参数自整定方法，该方法用量子比特构成染色体，用实数对量子比特进行编码；相比QGA，该方法将每个量子位看做上下2个并列的基因，每条染色体包含2条并列的基因链，每条基因链代表1个最优解。通过与普通遗传算法和标准量子遗传算法整定效果的对比，结果验证了DCQGA可以更快地跳出局部最优解从而获得更好的全局最优解，同时具有更快的响应速度和更好的多目标寻优能力。

参考文献：

[1] Ziegler J, Nichols N. Optimum Settings for Automatic Controllers[J].Transaction of ASME, 1942(64)： 759-768.

[2] 刘屿,田联房,毛宗源.一种新型人工免疫算法的PID自整定研究[J].计算机应用研究，2007，24(04)： 84-87.

[3] 陈书谦,张丽虹.蚁群算法在 PID 控制器参数优化中的应用研究[J].计算机应用研究,2011， 28(01)： 177-181.

[4] 余丽莹,焦嵩鸣.基于鱼群算法的PID优化[J].计算机仿真,2014,31(03)： 155-158.

[5] 彭勇,施宁,林浒.佳点遗传算法集及其在 PID控制中的应用[J].计算机应用研究,2009，26(02)： 524-526.

[6] 周明,孙树栋.遗传算法原理及应用[M].北京： 国防工业出版社,1999

[7] Narayanan A, Moore M.Quantum-inspired Genetic Algorithms[C]//Proceedings of IEEE International Conference on Evolutionary Computation. Nagoya, Japan, 1996： 61-66.

[8] Han Kuk-Hyun, Kim Jong-Hwan.Quantum-inspired Evolutionary Algorithm for a Class of Combinatorial Optimization[J]．IEEE Trans Evolutionary Computation, 2002, 6(06)： 580-593.

[9] Zhang G X, Gu Y J, Hu L, et al. A Novel Genetic Algorithm and Its Application to Digital Filter Design[C]//Proc on IEEE Intelligent Transportation System. New Jersey: IEEE Press, 2003, 2： 1600-1605．

[10] 商允伟，裘聿皇.适应值共享对遗传算法选择概率的影响分析[J]．控制与决策，2003，18(06)： 708-711.

[11] Li P C,Li S Y.Quantum-inspired Evolutionary Algorithm for Continuous Spaces Optimization[J].Chinese Journal of Electronics, 2008, 17(01)： 100-104.

[12] 李士勇,李盼池.基于实数编码和目标函数梯度的量子遗传算法[J].哈尔滨工业大学学报，2006(08)： 1216-1218.

[13] 张兴华,朱筱蓉,林锦国.基于量子遗传算法的PID控制器参数自整定[J].计算机工程与应用,2007(21)： 218-220.

[14] 郁磊，史峰.Matlab智能算法30个案例分析[M].北京： 北京航空航天大学出版社,2015.

[15] 曾成，赵锡均.改进量子遗传算法在PID参数整定中的应用[J].电力自动化设备,2009(10)： 125-127,139.

[16] 李士勇，李盼池.量子计算与量子优化算法[M].哈尔滨： 哈尔滨工业大学出版社,2009.

[17] Zhang G X,Li N,Jin W D.A Novel Quantum Genetic Algorithm and Its Application[J].ACTA Electronic Sinica, 2004, 32(03)： 476-479.

[18] 刘金琨.先进PID控制Matlab仿真[M].北京： 电子工业出版社,2011： 25-26.