刚性圆柱体涡激振动响应模态特性研究
冯绍军,熊友明,高 云
西南石油大学油气藏地质及开发工程国家重点实验室,四川成都 610500
圆柱体在一定的来流下,会在其尾部两侧形成交替脱落的漩涡,漩涡脱落会引起圆柱体产生周期性的振动,称为涡激振动(Vortex induced vibration,VIV)[1]。圆柱体涡激振动现象广泛存在于工程应用中,如处于空气中的桅杆、烟囱、桥梁悬索以及处于水中的立管、海底管道、锚链等结构,均有可能出现涡激振动响应。当尾部漩涡泄放频率靠近结构固有频率时,便会出现锁定现象,此时圆柱体会发生大幅的、危险的涡激振动响应,这种响应会给结构带来很大的疲劳损伤。
圆柱体涡激振动问题是一种典型的非线性流固耦合问题,该问题的研究方法主要分为实验方法[2-5]、计算流体动力学(Computational fluid dynamics,以下简称CFD) 方法[6-9]以及经验模型方法[10-13]。实验方法分析数据可靠、分析现象直观,但研究成本较高;CFD方法与经验模型方法之间最主要的一个区别在于流体力的获取,CFD方法可通过对模型的计算实时地获取流体力,而经验模型方法则是基于经验系数去近似地模拟流体力;显然CFD方法在计算精度上占有一定的优势,但经验模型方法在计算资源上更占优势,经验模型方法由于计算时间快,更适用于实际海洋工程中的多工况问题。尾流振子模型法则是应用较为广泛的一种经验模型方法。
本文以揭示刚性圆柱体涡激振动响应的模态特性为出发点,基于改进的尾流振子模型对刚性圆柱体的涡激振动响应模态特性展开了数值研究。具体研究内容如下:建立了结构以及尾流振子的无量纲耦合方程;对无量纲方程进行了线性简化,并通过解耦分析得到圆柱体涡激振动响应频率的实部、虚部以及升力与位移之间的相位差等参数;研究了不同质量比的圆柱体在不同折合速度下的涡激振动响应模态特性。
1 圆柱体与尾流振子耦合模型
在圆柱体涡激振动响应的模态特性分析过程中通常会出现4个特征频率[14]:第一个特征频率为圆柱体的结构固有频率ωn,该频率反映的是圆柱体的结构固有属性;第二个特征频率为依据斯脱哈尔漩涡泄放关系式计算得到的斯脱哈尔漩涡泄放频率ωf,值得注意的是该频率仅为一参考特征频率;第三个特征频率为结构发生涡激振动响应时结构的真实振动频率ωs;第四个特征频率为结构发生涡激振动响应时尾部流场的真实漩涡泄放频率ωw。
单位长度直径为D的刚性圆柱体在均匀来流U作用下引起的横流方向的涡激振动响应模型如图1所示。
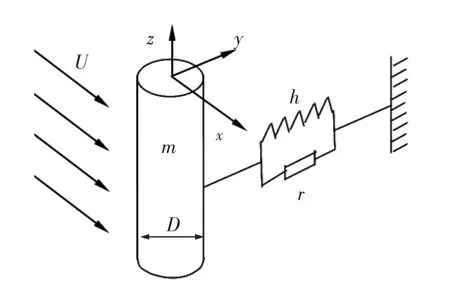
图1 刚性圆柱体涡激振动模型
取x方向为顺流方向,z方向为铅直方向,x、y以及z三个方向形成右手直角坐标系。刚性圆柱体在y方向产生横向位移Y,圆柱体的结构振动方程可以写为:
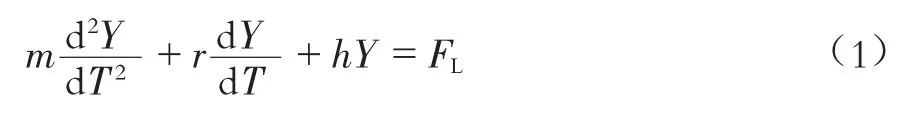
式中:T为时间;FL为升力;r为结构阻尼;h为结构刚度;m为单位长度的圆柱体质量,包括结构质量ms以及附加流体质量mf,可表示如下:
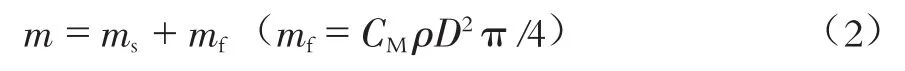
式中:ρ为流体密度;CM为附加质量系数,对于圆柱体,CM=1.0。
刚性圆柱体阻尼r包括结构阻尼rs和流体阻尼rf,可表示如下:
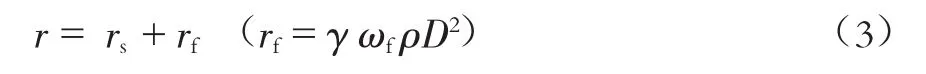
式中:γ为黏滞力系数,γ=CD/(4πSt),St为斯脱哈尔数。式(3) 中ωf为根据斯脱哈尔关系式计算得到的斯脱哈尔漩涡泄放频率(单位为rad/s),可表示为:

采用改进的Van der pol方程来满足尾流振子的非线性特性,表达式如下:
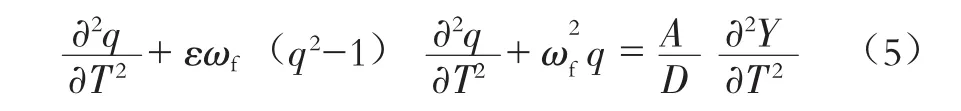
式中:ε为非线性项中的小参数;A为结构对流体的耦合动力参数;q为无量纲尾流振子变量,可表为:

式中:CL为流体对结构的瞬时升力系数;CL0是对应的静态圆柱体的横向升力系数幅值[15]。
将方程(1)和(5)转换成无量纲形式。令:

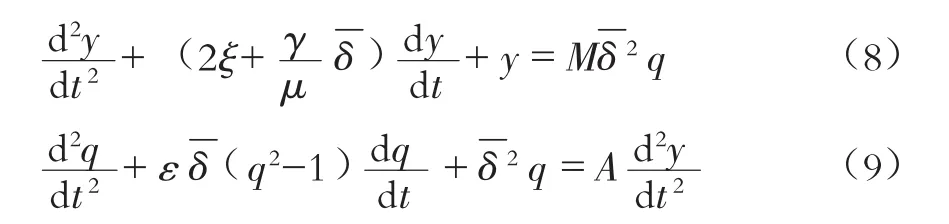
式中:所有的参数均为无量纲参数,其中t为无量纲时间,y为无量纲位移,ξ为圆柱体的结构阻尼比,以及μ为无量纲频率以及质量比,可表示如下:
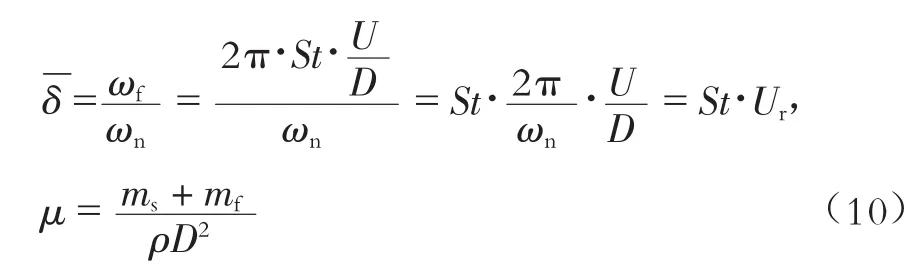
式中:ωn为结构的固有频率,Ur为折合速度。式(8)中M可写作:

2 耦合模型线性简化
由于本文侧重研究圆柱体系统响应的模态特性(频率特性),由结构动力学基础知识[16]可知,阻尼对系统频率特性影响较小。因此为了方便公式推导,假设式(8)以及式(9)的第二项(阻尼项)均为0,简化后表达式如下:

方程(12)和(13)的解表示为如下形式:
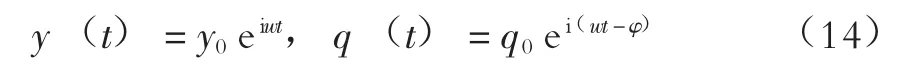
式中:y0为无量纲结构振动位移幅值,q0为无量纲升力振子幅值,φ为位移与升力振子之间的相位角;ω为无量纲频率,可表示为:

式中:ωs以及ωw分别表示圆柱体发生涡激振动响应时结构的真实振动频率以及尾部流场的真实漩涡泄放频率。将式(14)代入式(12)以及式(13)得到:
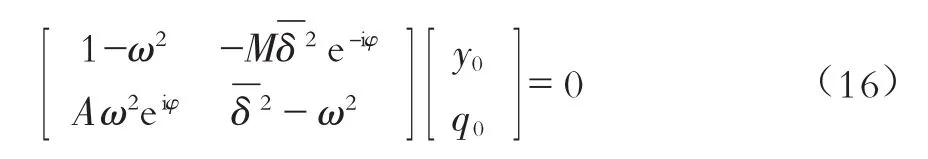
式(16)恒为0可得到左边第一项矩阵构成的行列式为恒为0,对其进行展开可得到频率特征方程:
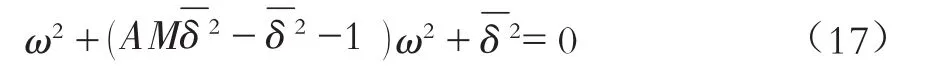
式(17)的解可表示为:
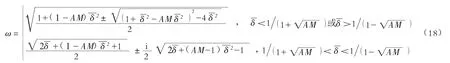
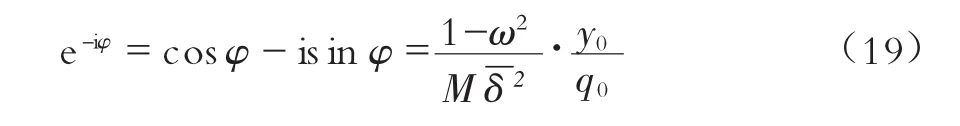
联合式(18)和式(19)可知:
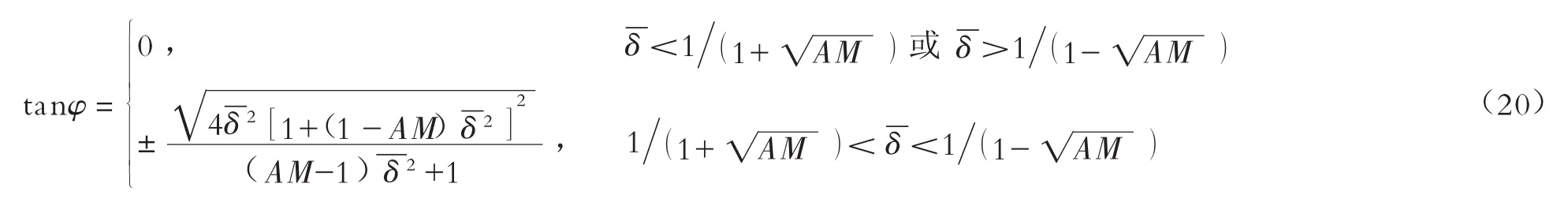
3 分析与讨论
本文分析了质量比μ对圆柱体涡激振动响应模态特性的影响,分析过程中研究了4种不同的质量比μ,分别为2、5、30、250。对于每种质量比μ,折合速度Ur区间取为0~15。图2到图5分别给出了μ=2、5、30、250这四种质量比时不同折合速度Ur下的圆柱体涡激振动响应模态特性,包括频率实部Re[ω],频率虚部 Im[ω]、频率比值 -Im[ω]/Re[ω]以及升力与位移之间的相位差φ。
由图2~5可以看出:对于某个特定质量比、特定折合速度,圆柱体涡激振动响应的频率实部Re[ω]存在两个值,第一个值接近圆柱体的斯脱哈尔漩涡泄放频率ωf(粉红色点划线),为流场模态的频率,即图中的尾部流场的漩涡泄放频率ωw(红色实线);第二个值接近圆柱体的固有频率ωn(水平黑色虚线),为结构模态的频率,即图中的圆柱体的结构振动频率ωs(蓝色虚线)。当折合速度较小时,ωw小于ωs;随着折合速度的上升,ωw会偏移斯脱哈尔漩涡泄放频率ωf,而逐渐偏向圆柱体固有频率ωn,该现象便是锁定现象,当折合速度处于锁定区间时,ωw等于ωs且出现在ωn附近;随着折合速度的进一步上升,ωw会再次偏移到斯脱哈尔漩涡泄放频率ωf附近,从而进入非锁定区间。针对锁定特性的研究主要有三方面:锁定开始点、锁定结束点以及锁定区间宽度。
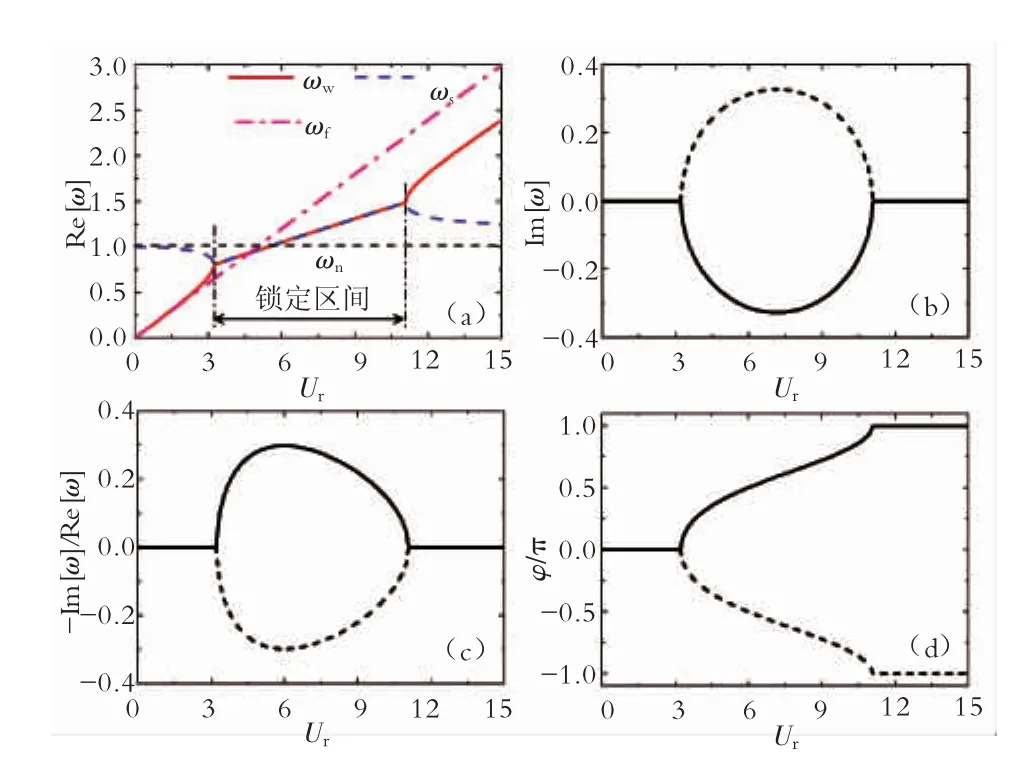
图2 圆柱体涡激振动响应模态特性(μ=2)
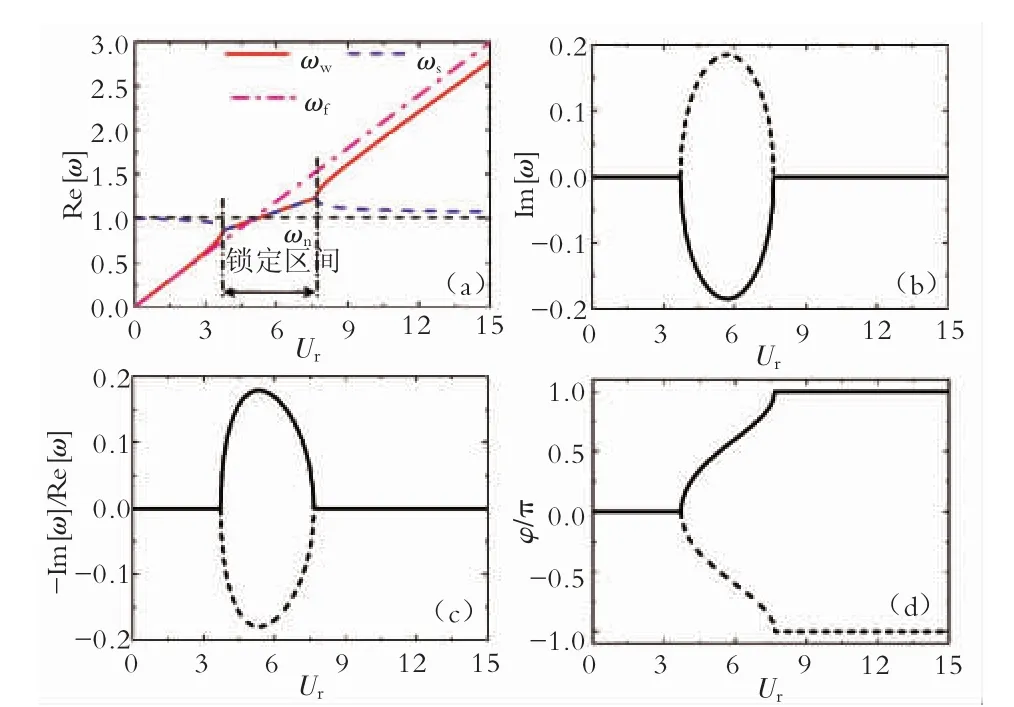
图3 圆柱体涡激振动响应模态特性(μ=5)
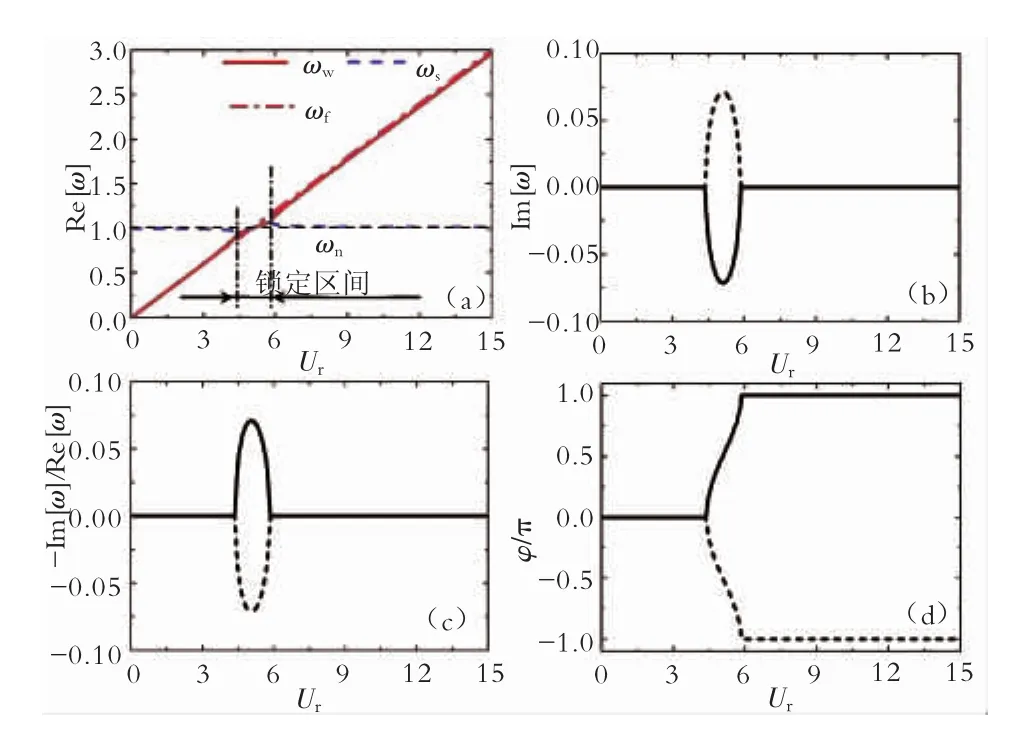
图4 圆柱体涡激振动响应模态特性(μ=30)
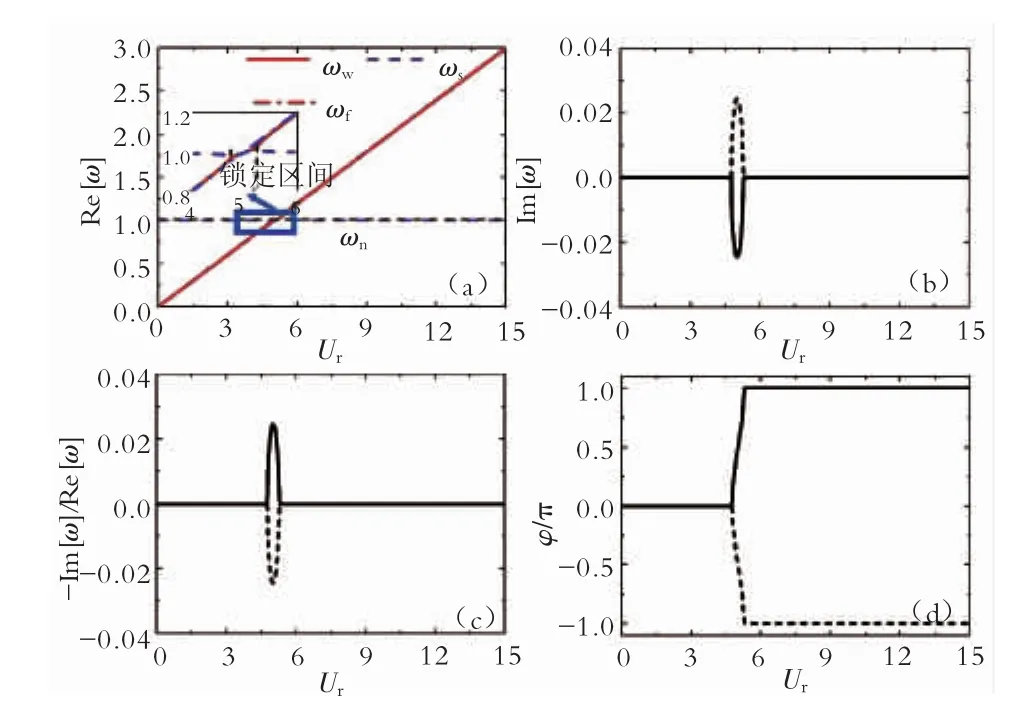
图5 圆柱体涡激振动响应模态特性(μ=250)
表1给出了四种质量比情况下圆柱体涡激振动响应发生锁定的开始点、结束点以及锁定区间宽度。
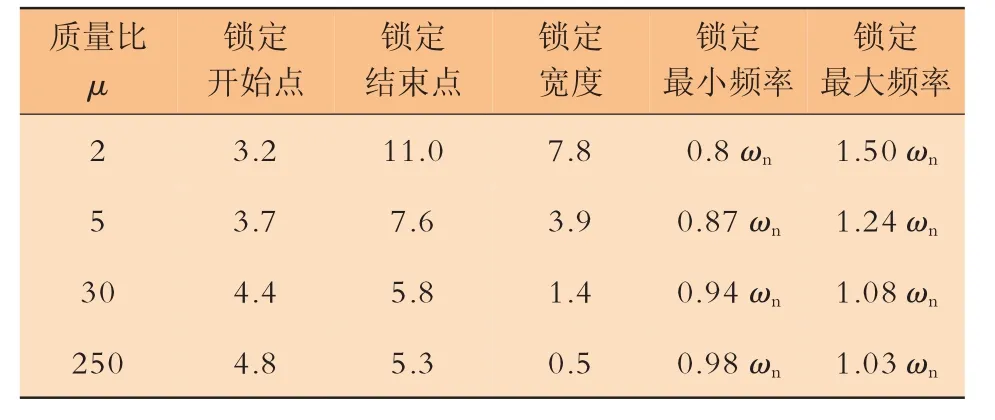
表1 不同质量比下的圆柱体涡激振动锁定响应特性
由表1可以看出:随着质量比的增加,锁定开始点逐渐延后,锁定结束点逐渐提前,锁定区间逐渐变窄。表1同样给出了当折合速度处于锁定区间时的圆柱体涡激振动响应频率的最小值以及最大值。可以看出:当折合速度处于锁定区间时,此时结构振动频率ωs(尾部漩涡泄放频率ωw)会出现在固有频率ωn附近,但是并不完全吻合。对于质量比较大(μ=250、300) 的圆柱体,ωs以及ωw与ωn吻合非常良好;但对于质量比较小(ωn=2、5)的圆柱体,ωs以及ωw明显偏移ωn,此时锁定区间的最小频率为0.8 ωn,而最大频率达到了 1.5 ωn。针对这种偏移现象,Sarpkaya给出了很好的解释[17]:圆柱体固有频率是处在静止流体中的结构固有频率。但当圆柱体发生振动时,结构的真实固有频率会逐渐偏移静止流体中的结构固有频率,这会导致与结构真实固有频率吻合的结构振动频率逐渐偏移静止流体中的结构固有频率,偏移量会随着质量比的减小而呈现上升趋势。对处于高质量比流体(如空气)中,偏移量可以忽略[18],这就会出现结构的振动频率非常接近结构在静止流体中的固有频率;但当结构处在低质量比流体(如水)中,这个偏移量则较为明显[19]。
图2到图5同样给出了频率的虚部Im[ω],频率虚部反映了振动的特性。可以看出:在锁定区间内,频率虚部存在一个正值以及一个与正值相反的负值。对于本文中的y=y0eiαt形式,频率虚部为正值(图中虚线)意味着圆柱体涡激振动响应为衰减振动,反应结构模态特性;频率虚部为负值(图中实线)意味着圆柱体涡激振动响应为不稳定振动,反应流场模态特性。锁定区间内,流场模态导致的振动为不稳定振动,且占主导。当折合速度历经锁定区间时,相位角φ由0逐渐变为π(图中实线)。当折合速度处于非锁定区间时,此时频率虚部为0,意味着结构模态以及流场模态均为稳定振动。
4 结论
本文基于改进尾流振子模型对刚性圆柱体的涡激振动响应模态特性进行了研究,研究了质量比对刚性圆柱体涡激振动响应模态特性的影响。通过研究得到如下结论:
(1)圆柱体的涡激振动响应模态可分为结构模态和流场模态两种。结构模态频率靠近圆柱体固有频率,而流场模态频率则靠近斯脱哈尔漩涡泄放频率。
(2)根据结构模态频率与流场模态频率是否相互吻合可以将涡激振动响应区间分为锁定区间以及非锁定区间。锁定区间宽度随着质量比的增加逐渐变窄。折合速度无论是处于锁定区间还是非锁定区间,流场模态均占主导。
(3)当折合速度处于非锁定区间时,由流场模态所产生的主导频率分布在斯脱哈尔漩涡泄放频率附近;当折合速度进入锁定区间时,主导频率会明显偏移斯脱哈尔漩涡泄放频率,而转移到结构固有频率附近。
[1]BLEVINS RD.Flow-induced vibration[M].Second ed.Malabar/Florida:Krieger Publishing,Inc,2001.
[2]张永波,郭海燕,孟凡顺,等.基于小波变换的顶张力立管涡激振动规律实验研究 [J].振动与冲击,2011,30(2):149-154.
[3]康庄,贾鲁生.圆柱体双自由度涡激振动轨迹的模型试验[J].力学学报,2012,44(6):970-979.
[4]高云,刘黎明,付世晓,等.柔性立管涡激振动响应轨迹特性研究 [J].船舶力学,2017,21(5):563-575.
[5]CHEN W L,ZHANG Q Q,LI H,et al.An experimental investigation on vortex induced vibration of a flexible inclined cable under a shear flow [J].Journal of Fluids and Structures,2015,54:297-311.
[6]唐友刚,樊娟娟,张杰,等.高雷诺数下圆柱顺流向和横流向涡激振动分析 [J].振动与冲击,2013,32(13):88-92.
[7]ZHANG H,FAN C F,CHEN Z H,et al.An in-depth study on vortex-induced vibration of a circular cylinder with shear flow[J].Computers and Fluids,2014,100:30-44.
[8]ZHAOM,CHENGL,ANHW,et al.Three-dimensional numerical simulation of vortex-induced vibration of a elastically mounted rigid circular cylinder in steady current[J].Journal of Fluids and Structures,2014,50:292-311.
[9]高云,王盟浩,宗智,等.高雷诺数时分离盘长度对圆柱绕流特性的影响 [J].上海交通大学学报,2017,51(4):504-512.
[10]陈伟民,张立武,李敏.采用改进尾流振子模型的柔性海洋立管的涡激振动响应分析 [J].工程力学,2010,27(5):240-246.
[11]郑中钦,陈伟民.结构与尾流非线性耦合涡激振动预测模型[J].海洋工程,2012,30(4):37-54.
[12]GROUTHIERC,MICHELINS,BOURGUETR,et al.On the efficiency of energy harvesting using vortex-induced vibrations of cables[J].Journal of Fluids and Structures,2014,49:427-440.
[13]XUK,GE Y,ZHANG D.Wake oscillator model for assessment of vortex-induced vibration of flexible structures under wind action[J].Journal of Wind Engineering and Industrial Aerodynamics,2015,136:192-200.
[14]GAO Y,FU S X,WANG J G,et al.Experimental study of the effects of surface roughness on the vortex-induced vibration response of a flexible cylinder [J].Ocean Engineering,2015,103:40-54.
[15]FACCHINETTI M L,de LANGRE E,BIOLLEY F.Coupling of structure and wake oscillators in vortex-induced vibrations[J].Journal of Fluids and Structures,2004,19:123-140.
[16]张亚辉,林家浩.结构动力学基础[M].大连:大连理工大学出版社,2007.
[17]SARPKAYA T.Fluid forces on oscillating cylinders[J].ASCE Journal ofWaterway,Port,Coastal,and Ocean Division,1978,104:275-290.
[18]FENG C.The measurement of vortex-induced effects in flow past a stationary and oscillating circular cylinder and D-section cylinders[D].Vancouver:University of British Columbia,1968.
[19]KHALAKA,WILLIAMSONCHK.Motions,forces and motion transitions in vortex-induced vibration at low mass-damping[J].Journal of Fluids and Structures,1999,13:813-851.

