连续搜索路径的最优化计算

陈建勇, 陈长康, 孙明军

(1. 海军航空大学电子信息工程系, 山东 烟台 264001;2. 海军航空大学研究生管理大队, 山东 烟台 264001)

0 引 言

最优搜索理论中,对连续随机运动的目标进行连续搜索的最优路径规划,仍是一项困难的工作。与其他形式的最优搜索问题相比,这一类问题尚没有系统的解决方法。文献[1-2]建立了搜索状态方程,并用射线法近似求解了搜索方程。文献[3-4]针对随机运动目标搜索问题,给出了目标位置概率密度函数和发现概率的计算方法。文献[5]讨论了目标的扩散方程,结合贝叶斯效应建立了最优搜索的最优控制问题。文献[6]根据给出的目标模型和搜索者探测概率模型,提出随机最优控制问题。文献[7-8]研究连续时空搜索问题,给出了最优轨迹的必要条件,将最优搜索路径问题化为最优控制问题。搜索路径的最优控制模型是具有一般性意义的最优搜索模型。文献[9]应用随机最优控制理论,求解了对一维环形路径上进行特定随机运动的目标进行搜索的最优搜索路径。文献[10]针对连续马尔可夫运动目标,建立了搜索者方向和速度均作为决策变量的搜索路径规划模型,给出了求解复杂搜索路径问题的改进双链遗传算法。文献[11]关于离散时间的最优路径优化问题,给出割平面法和线性化法两种求解方法。文献[12]针对三维空间离散时间最优路径优化问题,提出了分支定界法。

在讨论了搜索状态建模和一阶搜索状态方程求解的基础上,建立了连续搜索路径的最优控制模型,并给出了最优路径的逼近算法。在满足一阶搜索状态方程的随机恒速目标条件及有限指数探测函数条件下,应用本文的算法,给出了3个算例,分别求得了给定搜索起始点和搜索时间的最大发现概率搜索路径。

1 搜索状态方程及一阶方程的解

设t∈T=[0,T],令目标空间X⊂Rn,搜索空间Y⊂Rm。定义搜索路径函数Z,T→Y表示搜索者从0时刻搜索到T时刻所运动的轨迹,z=Z(t)表示t时刻搜索者所处的位置。

定义探测率函数b(x,t,z)。

定义搜索至t时刻未发现目标和目标位置的联合概率分布密度函数f(x,t,Z)。定义t时刻目标存在于x的条件下,从t时刻搜索到T时刻未发现目标的概率,即目标存活概率函数u(x,t,T,Z)。

目标在Δt内的随机移动向量具有二阶矩的条件下,有搜索状态方程[13]

(1)

(2)

式中,i、j表示空间维度；a(x,t)为速度均值函数向量;C(x,t)为目标随机移动量二阶矩的时间导数矩阵。

如果Cij=0,则搜索状态方程化为一阶方程。设向量函数和梯度向量均为列向量,一阶搜索状态方程为

b(x,t,z)u(x,t,T,Z)

(3)

-b(x,t,z)f(x,t,Z)

(4)

(5)

(6)

只要各个特征迹线不相交,那么,X空间中的任意一点就仅有一条特征迹线通过。应用终止条件u(x,T,T,Z)=1,初始条件f(x,0,Z)=ρ0(x),可以得到一阶搜索状态方程在特征线上的解为

(7)

f(x,t,Z)=ρ0(x0)·

(8)

式(7)中,x(τ),τ∈[t,T]是起点在x(t),终点在x(T)的特征线;式(8)中,x(τ),τ∈[0,t],是起点在x0=x(0),终点在x(t)的特征线。

按照联合概率分布密度函数f的定义,沿着轨迹Z搜索到t时刻,发现目标的概率为

(9)

对于任意t∈[0,T],沿Z搜索到T时刻发现目标的概率为

(10)

2 搜索路径的最优控制模型

在第1节对搜索状态建模和一阶搜索状态方程的求解,及给出发现概率模型的基础上,建立了连续搜索路径的最优控制模型。

令搜索路径函数Z(t)∈Rm为系统状态函数,搜索者的运动速度函数V(t)∈Rm为控制函数,则系统状态方程为

(11)

控制函数约束为|V(t)|≤Vm。

按照搜索路径Z从0时刻搜索到T时刻未发现目标的概率为

(12)

(13)

初始时刻为0,初始状态为Z(0),而终止时刻为t∈[0,T]的性能指标函数为

(14)

将式(13)表示成时间积分形式为

Jt+J[Z(t),t]

(15)

式中,J[Z(0),0]为初始时刻为t∈[0,T],初始状态为Z(t),终止时刻为T的性能指标函数。

构造哈密顿函数为

(16)

由动态规划原理知,对于使J[Z(0),0]取极小的Z*和V*,必使J[Z(t),t]取极小。

对于所有t∈[0,T],存在向量λ*(t),使得下列HJB(Hamilton-Jacobi-Bellman)方程成立,表示为

(17)

式中[13]

(18)

由于

(19)

(20)

得到

(21)

3 最优搜索路径逼近算法

基于对搜索状态建模和一阶搜索状态方程的求解,建立了连续搜索路径的最优控制模型,结合动态规划原理,最优搜索路径的逼近算法流程图如图1所示。

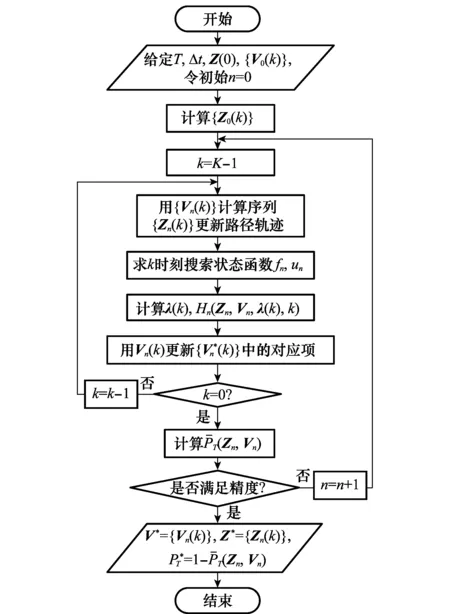
图1 最优搜索路径逼近算法流程Fig.1 Flow chart of optimal search path approximation algorithm

算法具体计算步骤如下。

步骤2给定初始搜索速度的向量序列{V0(k)},k=0,1,2,…,K-1;n=0;k=K-1;

步骤3根据向量序列{Vn(k)},计算路径轨迹为Zn(k+1)=Zn(k)+Vn(k)Δt;

步骤4求k时刻一阶搜索状态方程的特征迹线解un、fn,un、fn空间中一点的求解如式(7)、式(8)所示,特征迹线求解为式(27);若k=-1,转到步骤8;

步骤5在求得空间值un、fn下,结合式(28)计算b(x,t,Z(t),V(t)),由式(21)、式(16)分别计算λ(k)、Hn(Zn,Vn,λ(k),k);

4 算 例

4.1 目标模型

由于从信息源获得的目标位置数据具有不确定性,定位误差的随机性构成了目标初始位置的随机性。用圆正态分布描述目标的初始位置分布,依据的是定位误差的分布。而在没有目标航向判断依据的情况下,目标速度的圆正态分布是最为恰当的设定分布。

设初始时刻为0,目标空间为二维空间,目标的初始位置分布服从圆正态分布

(22)

设目标为随机恒速运动目标,其速度分布为圆正态分布

(23)

在t时刻，目标速度的空间条件分布为[14]

(24)

在x点的目标速度期望值及其散度[14]为

(25)

(26)

任意x(0)点所在的特征线方程[14]为

(27)

证明可得,研究的随机恒速运动目标满足一阶搜索状态方程。

计算中取σ=2 nm,μ=8 kn。

4.2 探测模型

设搜索空间为二维空间,根据文献[15]针对潜艇给出的探测模型,令探测率函数为

b(x,t,z)=

(28)

取探测器作用距离R=1 nm。

搜索起始时刻为0,终止时刻为T,设搜索速度|V|=300 km/h,目标和搜索空间计算范围为50 nm×50 nm,坐标原点设在计算区域的中点。

4.3 算例1

设Z(0)=(-11 nm,-11 nm),T=15 min。

搜索起点、初始路径经12次路径逼近计算得到满足精度要求的最优路径及相应的发现概率如图2所示。

4.4 算例2

将算例1最优路径的终点作为搜索起点,即Z(0)=(-2.9 nm,0.6 nm),T=15 min。

搜索起点、初始路径经10次路径逼近计算得到满足精度要求的最优路径及相应的发现概率如图3所示。

图3 算例2的初始路径和最优路径Fig.3 Initial path and the optimal path of the second analysis example

4.5 算例3

设Z(0)=[-22 nm,-22 nm],T=15 min。

搜索起点、初始路径经9次路径逼近计算得到满足精度要求的最优路径及相应的发现概率如图4所示。

图4 算例3的初始路径和最优路径Fig.4 Initial path and the optimal path of the third analysis example

5 结 论

基于搜索状态函数f、u和搜索路径函数Z的发现概率模型,是对发现概率的精确描述。但即使最简单的目标随机运动模型和搜索者约束,也无法获得搜索路径的最优化解析解。根据动态规划原理,设计了最优路径的逼近算法。多个算例表明,该算法能够收敛到一条最优路径上。关于算法收敛性以及局部最优与目标随机性特征的关系,还需要进一步的工作。

参考文献：

[1] HELLMAN O. Optimal search for a randomly moving object in a special cases[J]. Journal of Applied Probability, 1971, 8(3): 606-611.

[2] MANGEL M. Search for a randomly moving object[J]. SIAM Journal of Applied Mathematics, 1981, 40(2): 327-338.

[3] HELLMAN O. On the optimal search for a randomly moving target[J]. SIAM Journal of Applied Mathematics,1972,22(4): 545-552.

[4] MANGEL M. Probability of success in the search for a moving target[J]. Operations Research, 1982, 30(1): 216-222.

[5] HELLMAN O. On the effect of a search upon the probability distribution of a target whose motion is a diffusion process[J]. The Annals of Mathematical Statistics,1970,41(5):1717-1724.

[6] OHSUMI A. Stochastic control with searching a randomly moving target[C]∥Proc.of the American Control Conference, 1984: 500-504.

[7] LUKKA M. On the optimal searching tracks for a moving target[J]. SIAM Journal of Applied Mathematics, 1977, 32(1): 126-132.

[8] FORAKER III J C. Optimal search for moving targets in continuous time and space using consistent approximations[D]. Monterey California: Naval Postgraduate School, 2011.

[9] 朱清新,卿利,彭博.随机运动目标搜索问题的最优控制模型[J].控制理论与应用,2007,24(5):841-845.

ZHU Q X, QING L, PENG B. Optimal control model of search problem for randomly moving targets[J]. Control Theory & Applications, 2007, 24(5): 841-845.

[10] 张献,任耀峰,沈静.连续时空最优搜索者路径问题的改进双链遗传算法[J].系统工程与电子技术,2015,37(5):1092-1098.

ZHANG X, REN Y F, SHEN J. Improved double chains genetic algorithm for optimal searcher path problem in continuous time and space[J].Systems Engineering and Electronics,2015,37(5): 1092-1098.

[11] ROYSET J O, SATO H. Route optimization for multiple searchers[J].Naval Research Logistics,2010,57(8):701-717.

[12] SATO H, ROYSET J O. Path optimization for the resource-constrained searcher[J].Naval Research Logistics,2010,57(5),422-440.

[13] 陈建勇. 单向最优搜索理论[M]. 北京:国防工业出版社, 2016: 156-169.

CHEN J Y. One-side optimal search theory[M]. Beijing: National Defense Industry Press, 2016: 156-169.

[14] 陈建勇,张驰.随机恒速运动目标的搜索方程及持续探测概率[J].海军航空工程学院学报,2015,30(6): 521-525.

CHEN J Y, ZHANG C. Search equation for a moving target with random constant velocity and the probability of persistence detecting[J]. Journal of Naval Aeronautical and Astronautical University, 2015, 30(6):521-525.

[15] ALIEXANDRIDIS M G. Mathematical formulation of the ASW decision model[M]. Cognitive Simulation of Anti-submarine Warface Commander’s Tactical Decision Process. American office of Navy Research,1984: 55-59.