基于模拟退火算法的快速登机序列特性研究

强生杰，贾 斌，黄青霞

(1.华东交通大学交通运输与物流学院，南昌330013；2.北京交通大学交通运输学院，北京100044)

0 引言

我国民航运输业在快速发展的同时也面临着严峻挑战，尤其是高速铁路的快速发展对旅客出行结构产生了重大的影响.降低客机的周转时间可提高现有航空资源的利用率，提升航企核心成本竞争力.登机时间是客机周转时间中最重要的组成部分，它在短途航线中占到了总旅行时间的40%～60%[1].虽然登机耗时并非航空公司高昂成本的主要原因，但若使用高效稳定的登机策略，航空公司和机场管理者便可降低运营和管理成本.Nyquist等[2]经过调查统计出周转时间内每减少1 min就会节省约30美元(保守估计)的费用，对于一个每天执行5 000次航班的大型航空公司而言每年可节省约5 000万美元的费用.

现有登机方式的效率低下，如随机登机或从后往前的分组登机方式(Back-to-front，BF)，这是因为上述登机方式无法避免以下2种干扰：一是过道干扰(Aisle Interference)，当1位乘客到达其指定的座位后，会占据过道空间来存放自己的行李，从而阻挡了后续乘客的移动；二是座位干扰(Seat Interference)，其发生在已经就座在靠近过道一侧的乘客阻挡了同侧同一行靠窗乘客的就座，若该干扰发生，那些已经就座的乘客就必须起身让道而造成额外的时间延误.

合理有序的组织乘客登机可提高航班和机场运行效率.鉴于此，国内外学者对航空登机问题进行了研究.Van Landeghem等[3]在分析Belgian Airline数据的基础上建立了离散的登机仿真模型并发现随机登机优于BF策略.同样的，Mas等[4]研究了若干登机方式在3种不同机型下的效率，结果表明BF策略并不是一种高效的方法.Ferrari等[5]利用仿真模型研究了在不同登机环境下的登机时间稳定性.Steffen[6]利用马尔可夫—蒙特卡洛优化算法发现了高效的登机策略.Notomista等[7]利用图像识别技术来快速的检测乘客的个人属性并以此提出了一种座位分配算法.尚华艳等[1]首次利用双曲线模型来计算乘客存放行李的时间.刘洋等[8]利用蒙特卡洛模拟方法发掘出一种针对中型客机的优化策略.刘山等[9]提出了“组队”的概念并以此设计出一种改进的新登机模式.唐铁桥等[10-11]首次建立了可应用于登机模拟的乘客运动连续模型，并首次提出了根据乘客个体特征来安排登机顺序的新方法.强生杰等[12]在Steffen等工作的基础上提出了考虑行李分布的快速登机策略.任新惠等[13-15]总结对比了多种单通道登机策略的效率，并在仿真的基础上提出了一些设计登机策略的建议.

注意到以往的研究思路是先提出一种新的登机策略，然后利用仿真模拟方法去验证其有效性，却很少关注登机效率与登机乘客序列之间的关系.为了完善这部分研究的空白，本文将利用模拟退火算法求解出最小登机时间对应的若干最优登机序列，并通过对比分析出这些高效率登机序列中共有的特征序列，从而为实际航空登机过程提供理论指导.

1 基于元胞自动机的乘客登机仿真模型

为了便于问题的讨论，模型的基本假设有：研究对象为短途航线使用的窄体客机；只设置1个登机口；只探讨经济舱乘客的登机过程，其他人员包括头等舱及需要特殊服务的乘客由于提前登机，不在本模型的考虑范围之内；乘客是独立出行且同质的，具有相同的物理属性(如移动速度及体型)；乘客存放行李的时间均相同；客机过道的宽度狭窄，乘客只能跟随前进不能越行；只研究乘客在登机前已预先分配座位号的情况，即登机牌中明确标注了座位的位置.

1.1 客机机舱描述

图1为一个标准的客机经济舱座位布局，座位划分为6列25行，且对称地分布在单过道的两侧.在元胞空间中，客机机舱被划分为离散的座位及过道元胞，在登机过程中每个元胞或者是空的，或者被1位乘客占用.每个座位由唯一的坐标(r,c)来表示，其中r∈{1,2,…,25}，c∈{A,B,C,D,E,F}，A、F代表靠窗位置，B、E代表中间位置，C、D代表过道位置.如坐标(15,C)代表位于第15行靠过道的座位.

图1 机舱内部空间元胞示意图Fig.1 Schematic illustration of airplane cabin in cellular space

1.2 乘客跟随模型

乘客i在第t时间步的运动状态可用其位置及速度信息来刻画，分别用xi(t)和vi(t)表示.在时间步t→t+1的过程中，模型采用如下3个规则来并行更新乘客的运动状态：

R 1加速.每个乘客期望以最短的时间到达指定的座位，因此他们试图以最大的速度vmax在过道里移动.

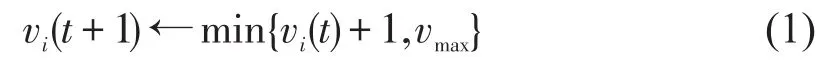
R 2减速.该规则避免了乘客与前面的乘客发生碰撞(按照模型的假设受阻挡的乘客不能越行).

式中：Gi(t)为乘客i前方的空格子数，考虑到每个乘客必须在其指定的座位处停留进而存放行李，因此Gi(t)可定义为

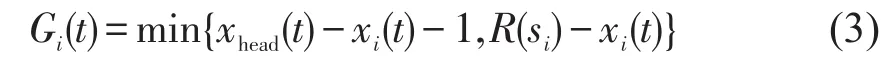
式中：xhead(t)为过道中乘客i前面乘客的位置.式(3)右边括号内第1部分的含义为该乘客与其前面乘客之间的空元胞数；第2部分代表该乘客距离其目标座位的元胞数，其中R(si)将乘客i的目标座位si映射为其对应的过道元胞位置.

R 3乘客运动.

1.3 登机过程仿真流程

登机过程模拟的流程包括以下3个步骤.

Step 1参数设置.

设定登机人数N及乘客运动参数的数值，需额外设置的辅助变量有已就座乘客的数目Nsit和登机时间T，初始时为Nsit=0，T=0.

Step 2登机过程.

模型采用并行规则来更新乘客的运动状态，具体为：

(1)检 票.

每位乘客需花费Tcheck个时间步来接受检票.对于检票完毕的乘客，若机舱过道内的第1个元胞未被占用则其可进入客机机舱，否则滞留在检票口处.

(2)乘客在机舱过道内移动.

①若乘客i未到达指定的座位，则利用1.2节中介绍的乘客跟随模型来更新其状态.若xi(t+1)=R(si)，则意味该乘客已经到达指定座位对应的过道元胞，其会停在该处(vi(t+1)=0)去存放行李并处理可能的座位干扰，其占用过道的时间步为

式中：tstore为乘客存放行李所需的时间步(所有乘客均相同)；为乘客i处理座位冲突的时间步，其值与座位干扰的次数Mi(如图2所示)相关，数值为

②若乘客i已在其指定座位对应的过道处，则检查变量的数值.若，则该乘客仍在存放行李或处理座位冲突，其状态保持不变，即vi(t+1)=0，xi(t+1)=xi(t)，但；若，则该乘客已经处理完所有的行李和座位干扰并就座，其个人的登机过程结束，同时令Nsit=Nsit+1.

Step 3登机结束判断.

统计已就座乘客的数目Nsit，若Nsit=N，则表示所有的乘客已就座，登机过程结束，最终的登机时间为T=t+1；若Nsit≠N，则表示尚有乘客未就座，重复执行Step 2中的各项规则.

图2 登机过程中的座位干扰次数MFig.2 Number of interfering passengersMwhen boarding

2 模拟退火算法

模拟退火(Simulated Annealing,SA)是一种基于Monte-Carlo迭代求解过程的随机寻优算法，Metropolis准则是一种以概率收敛于全局最优解的全局优化算法.其求解流程为：对每一个温度Temp进行迭代并利用Metropolis准则对解进行取舍，伴随温度参数的下降结合概率突跳特性在解空间中随机寻找目标函数的全局最优解.

在登机问题中，乘客个体的每一种登机序列对应于算法中的固体降温状态，而登机时间的大小为该状态下能量的取值.基于这种假设，我们可以借助模拟退火算法求解出1个登机过程所消耗的最小登机时间，以及最小登机时间下所对应的乘客登机序列.对于1次寻优过程，算法实现的流程如图3所示，具体为：

(1)初始化.设置系统初温Temp的数值，随机选取1个初始登机序列ω，确定外层循环结束温度值TEPS，内层循环的迭代次数L及温度衰减系数φDelta.

(2)内层循环，对K=1,2,…,L依次进行如下的步骤.

①在禁忌约束条件下随机互换2位乘客的位置，生成新的登机序列ω′.

② 计算登机时间的变化量ΔT=T(ω′)-T(ω)，其中T(ω)为登机序列ω对应的登机时间，其数值可通过第2节介绍的登机仿真模型来获取.

③若ΔT＜0，意味着新序列ω′可降低登机时间，接受其作为新的当前解；否则以一定的概率exp(-ΔT/Temp)接受ω′作为新的当前解.

④如果满足终止条件，则输出当前解作为最优解，结束内层循环.

(3)外层循环，若Temp＜TEPS，则输出最优登机序列，结束外层循环，寻优过程结束；否则，令Temp=Temp⋅φDelta，转第(2)步，继续寻找在温度Temp下的最优解.

为加快求解速度，避免产生无效的登机序列 而增加时间开销，算法需设置禁忌约束条件：由于座位布局的对称性，交换2个在同排且座位均为靠过道的乘客位置不会产生新解，因而在生成新解的过程中上述交换是被禁止的.

3 模拟计算与结果分析

3.1 参数设置

模拟退火算法中的参数设置为：初始温度Temp=2 000，终止温度TEPS=1.0×10-8，内层循环迭代步数L=2 000，温度衰减系数φDelta=0.99.登机模型中乘客的速度均被整数化，乘客的最大速度为vmax=1(元胞/时间步).Van Landeghem等[3]采用三角形分布来描述乘客在机舱内通过1行座位的时间，其下限是1.8 s，众数为2.4 s，上限是3 s.与上述研究保持一致，此处我们设定乘客通过1行座位(格子)的时间为2.4 s.乘客在登机口以一定的时间间隔接收检票，人均检票时间Tcheck=2个时间步.注意本文结果均以仿真时间步为标准，若转化为实际的登机时间，则需要乘以2.4 s.

3.2 过道及座位干扰对登机时间的影响

图4显示了在2种存放行李时间tstore=0和tstore=5下，利用模拟退火算法来寻找最小登机时间的过程，同时也统计了人均座位干扰次数随登机序列变化的过程.结果表明，乘客登机时间随着系统温度的降低逐渐减少，并最终趋于一个较为稳定的数值.对比图4中的2种情况，可以发现即便乘客处理行李的时间为零，如图4(a)所示，在登机时间稳定在局部最小值的时候人均座位干扰次数仍处于无规律的波动状态.同样的，若乘客需要一定的时间去存放行李，如图4(b)所示，虽然会使得最小登机时间较无行李存放的情况有所增加，但人均座位干扰分布同样呈现出无规律性的波动性.

图4 最小登机时间寻优过程Fig.4 Process of searching the minimum boarding time

减少乘客座位冲突的次数会减少乘客额外的过道占用时间，从而会降低座位通道处局部拥堵发生的概率.但上述数值结果表明，人均座位干扰次数不会随着登机时间的减少而逐步降为零.这意味着减少座位干扰次数对减少登机时间的贡献并不是最主要的，通过合理调整乘客间的序列关系，即便发生了局部的座位干扰，只要其不会演变为对过道中后续乘客的过道干扰，那么其也不会影响到总登机时间.

为了进一步说明导致登机延误中座位干扰及过道干扰的影响程度，在相同的模拟及优化参数设置下，图5分布绘制了2种行李存放时间下最小座位冲突次数的寻优过程.可以发现，随着温度数值的降低，座位干扰次数也随之降低并最终达到最小值零，意味着该登机序列下的乘客座位干扰次数完全消失，但其对应的登机时间并未达到图4对应情况下的最小值，并且时间波动性也非常大.数值结果再次证明登机过程中即便完全消除了座位干扰数，也不一定会得到最小的登机时间.这也从一个方面说明过道干扰才是引起登机时间延误的主要因素，而座位干扰的影响是次要的.

图5 最小座位干扰次数寻优过程Fig.5 Process of searching the minimum number of seat interference

3.3 快速登机序列特征

为方便发掘快速登机序列中的序列共性，在此引入变量dis(k)，其定义为第k个进入机舱乘客的座位与基准座位(1,A)之间的距离(使用座位数来表征).在图6划分的坐标中，若第k∈[1,150]个进入的乘客的目标座位为(rk,ck)，则

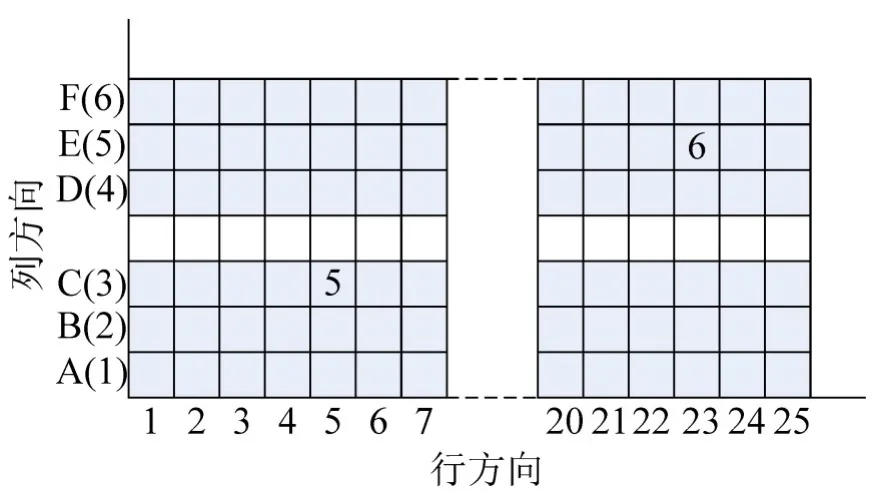
图6 客机座位布局平面坐标系Fig.6 Coordinates of airplane seat layout

在此基础上可进一步定义第k个进入的乘客与其前面的第k-1个乘客的座位距离差ΔD(k).

例如，图6中第5个进入的乘客的dis(5)=27，第6个进入的乘客的dis(6)=137.则ΔD(6)=特别的，第1个进入机舱乘客的ΔD(1)=0.

图7统计了1 000次经过模拟退火算法求得的在4种不同的行李存放时间下最优序列中乘客ΔD数值的分布.结果表明：

(1)如图7(a)所示，若乘客均不携带行李，即tstore=0，那么就无需组织乘客的登机序列，因其相邻乘客间的座位间距分布情况与随机登机过程的分布大致相似.

(2)随着乘客存放行李的时间增多，如图7(b)～图7(d)所示，出现1个明显的峰值，且峰值大约位于第7个座位的距离处，这个数值恰好是1位乘客在处理行李时占据1个过道元胞所跨越的最小座位间隔数.

(3)此外，分布峰值的高度会随着时间tstore的增大而增大，同时其他的座位距离的分布更加集中，这意味着若乘客占据较长的过道时间，那么相邻乘客之间座位距离就应向峰值位置处靠近.

3.4 启 发

首先，座位干扰和过道干扰对登机时间的影响是不同的，在策略设计中要重点考虑过道干扰，同时要避免发生座位干扰转化为过道干扰的情况.导致乘客长时间停留在过道中的原因是其需要花费时间去存放行李，当乘客携带行李较多时，这个延误效果非常明显.这就需要在设计登机策略的时候考虑乘客行李在机舱行李架中的分布或者对乘客登机时所携带行李的数量及尺寸进行严格的控制.例如，强生杰等[12]提出了考虑行李分布的快速登机策略，具体为：同一个分组内中的乘客按照座位从后往前的顺序登机，且携带行李较多的旅客率先登机.上述策略大大降低了乘客携带行李数目对登机过程的影响，具有较高的登机效率及时间稳定性.

其次，需要合理的设置登机序列中两个相邻进入乘客间的座位.例如，Steffen[6]假设每个人需占据2个座位的长度，其小组内相邻乘客间的座位距离均为ΔD=12.但实际上乘客只需占据1个座位长度的过道空间就可完成存放行李等活动，因而本模型中只假设每位乘客占据1个过道元胞.此时可考虑如下的优化策略：乘客按列编号被划分为6个分组，每个小组内包含25位乘客，每个小组内的乘客依照座位的编号从机舱的后部往前就座.这样每个小组内的相邻乘客间的座位距离均为ΔD=6.上述策略避免了分组内乘客间的过道干扰，且多人同时处理行李可大幅提高过道的利用率.

图7 最优解序列中乘客座位间隔分布图Fig.7 Seating distance distribution in the optimized sequence

此外，也可考虑采用动态的座位分配算法，即乘客在检票的同时会自动的分配座位，其核心的算法需考虑相邻进入乘客的座位间隔，使其尽可能的不产生相互干扰.一般的快速登机策略均需在检票口设置预登机排队区域，这就额外增加了机场管理者的组织负担，而自动分配座位策略则避免了工作人员的负担同时实现快速登机.

4 结论

本文利用模拟退火算法来挖掘最小登机时间对应的登机序列的序列特性，结果表明：当人均存放行李时间增大时，相邻登机的乘客应尽可能隔行就座.这样的好处是减少了过道干扰次数，同时允许若干乘客互不干扰(并行)的存放行李会进一步缩短登机时间.注意到，本文中每位乘客存放行李的时间是相同的，实际上乘客携带行李的数目是不同的，行李架中可存放行李的空间也是动态变化的.这导致行李存放时间不仅与自身携带行李的数目相关也与登机序列相关，此时最优序列中的序列特征有待进一步研究.

参考文献：

[1]尚华艳,陆化普,彭愚.基于元胞自动机的乘客登机策略[J].清华大学学报(自然科学版),2010,50(9):1330-1333.[SHANG H Y,LU H P,PENG Y.Aircraft boarding strategy based on cellular automata[J].Journal of Tsinghua University(Science&Technology),2010,50(9):1330-1333.]

[2]NYQUIST D C,MCFADDEN K L.A study of the airline boarding problem[J].Journal of Air Transport Management,2008,14(4):197-204.

[3]VAN LANDEGHEM H,BEUSELINCK A.Reducing passenger boarding time in airplanes:A simulation based approach[J].European Journal of Operational Research,2002,142(2):294-308.

[4]MAS S,JUAN A A,ARIAS P,et al.A simulation study regarding differentaircraftboarding strategies[M]//Modeling and Simulation in Engineering,Economics,and Management,Springer Berlin Heidelberg,2013.

[5]FERRARIP,NAGEL K.Robustnessofefficient passenger boarding strategies for airplanes[J].Transportation Research Record:Journal of the Transportation Research Board,2005(1915):44-54.

[6]STEFFEN J H.Optimal boarding method for airline passengers[J].Journal of Air Transport Management,2008,14(3):146-150.

[7]NOTOMISTA G,SELVAGGIO M,SBRIZZI F,et al.A fastairplane boarding strategy using online seat assignment based on passenger classification[J].Journal of Air Transport Management,2016(53):140-149.

[8]刘洋,刘振兆,贾利民.一种高效的登机策略[J].交通运输系统工程与信息,2008,8(5):118-123.[LIU Y,LIU Z Z,JIA L M.Adaptive approach to aircraft boarding strategy[J].Journal of Transportation Systems Engineering and Information Technology,2008,8(5):118-123.]

[9]刘山,李天顺,于立庚,等.关于登机时间优化的新模式[J].中国民航大学学报,2008,26(2):50-52.[LIU S,LI T S,YU L G,et al.New optimal mode for boarding time[J].Journal of Civil Aviation University of China,2008,26(2):50-52.]

[10]TANG T Q,WU Y H,HUANG H J,et al.An aircraft boarding model accounting for passengers’individual properties[J].Transportation Research Part C:Emerging Technologies,2012(22):1-16.

[11]TANG T,HUANG H,SHANG H.A new pedestrianfollowing modelfor aircraft boarding and numerical tests[J].Nonlinear Dynamics,2012,67(1):437-443.

[12]QIANG S J,JIA B,XIE D F,et al.Reducing airplane boarding time by accounting for passengers'individual properties:A simulation based on cellular automaton[J].Journal of Air Transport Management,2014,40(C):42-47.

[13]任新惠,唐少勇.单通道客机旅客登机策略比较研究[J].交通运输系统工程与信息,2014，14(4):173-179.[REN X H,TANG S Y.Comparative study of boarding strategies for single-aisle aircraft[J].Journal of Transportation Systems Engineering and Information Technology,2014，14(4):173-179.]

[14]任新惠,唐少勇.单通道客机登机策略模拟研究[J].科学技术与工程,2015(1):120-126.[REN X H,TANG S Y.The simulation study of single aisle aircraft boarding strategy[J].Science Technology and Engineering,2015(1):120-126.]

[15]任新惠,张思雨.航空旅客登机策略研究综述[J].长安大学学报(社会科学版),2016,18(1):30-35.[REN X H,ZHANG S Y.Overview of researches on passengers aircraft boarding[J].Journal of Chang'an University(Social Science Edition),2016,18(1):30-35.]