带时间窗的甩挂运输路径优化问题研究

边 展，徐 奇，靳志宏*

(1.首都经济贸易大学工商管理学院，北京100070；2.大连海事大学交通运输工程学院，辽宁大连116026)

0 引言

由于消费者对于货品送达时间的要求愈加严格，企业必须思考如何在更短时间内以较低的运输成本满足客户需求.因此，带时间窗的车辆路径问题(VRPTW)日益受到重视.甩挂运输路径优化问题(TTRP)为VRP的衍生，Chao[1]以最小化车队总成本或总行驶距离为目标，建立数学模型，并将21个经典VRP算例改进为TTRP算例.针对该21个算例，Lin[2]运用模拟退火算法求得了其中的17个最优解.Villegas等[3]对多场站单车辆的TTRP问题进行研究，设计并改进了GRASP/VND算法.Derigs等[4]考虑了卡车与拖车之间的货物转移，采用基于局部搜索、大规模邻域搜索与标准泛启发式算法的混合算法进行求解.李红启等[5]针对城际干线甩挂运输过程所涉及的卡车调度这一问题开展研究，建立了整数规划模型，并运用模拟退火算法进行求解.基于此，李红启等[6]考虑运输过程中的碳排放量，通过数值实验验证了TTRP的节能减排效果.

分析现有研究不难发现，针对TTRP问题鲜有同时考虑时间窗约束及拖车调度情形，且拖车停放点通常是随机选取或选择停放成本最低的客户点.而本研究不仅纳入时间窗因素，还考虑了现实作业中拖车只能停放在特殊客户点的约束，同时优化卡车路径与拖车路径，从而更加符合实际运输情形.

1 问题描述与假设条件

甩挂运输的整车可以分为卡车与拖车2个部分，如图1所示.卡车与拖车均可承载货物，拖车无动力，须附挂于卡车上.卡车可将拖车卸下，单独以一般卡车的形式行驶，绕行子路径后重新与拖车接回，以整车形式继续服务.

图1 甩挂运输示意图Fig.1 Illustration of the truck-trailer transportation

因此，可将客户划分为仅由卡车配送的卡车客户及由整车或卡车配送的整车客户，相应地，行驶路径可划分为卡车路径，如图2(a)所示；整车路径，如图2(b)所示；混合路径，如图2(c)所示.

图2 配送示意图Fig.2 Illustration of the truck-trailer distribution

本研究的TTRPTW可归纳为：利用卡车—拖车的整车配送或卡车单独配送的方式满足不同服务时间的客户需求.假设条件如下：

①卡车客户只能以卡车进行配送，整车客户可以整车或卡车进行配送.

②以整车配送的客户仅有部分可作为拖车停放点.

③不考虑车辆固定成本及拖车停放费用.

④仅考虑场站与客户的时间窗上限.

2 符号描述与建模

2.1 符号定义

(1)标 号.

h,i,j——节点标号；

k——所有车辆标号；

t——卡车标号；

v——拖车标号.

(2)车辆集合.

T——卡车集合；

V——拖车集合.

(3)节点集合.

0——场站；

N0vt——场站与路网中的所有节点；

Nvt——路网中的所有节点；

N0v——场站与能以整车服务的节点；

Nv——能以整车服务的节点；

Np——拖车停放点的集合.

(4)参 数.

qi——节点i的需求量；

Qt——卡车的载重上限；

Qv——拖车的载重上限；

Li——节点i的配送时间窗上限；

Si——节点i的服务时间；

Tp——在拖车停放点拆卸及组装拖车的时间.

(5)变 量.

di——离开节点i的时间；

ai——抵达节点i的时间；

d2i——第2次离开节点i的时间；

a2i——第2次抵达节点i的时间.

2.2 模型建立

目标函数式为

式(1)为最小化车辆行驶时间，由卡车行驶总时间与整车行驶总时间构成.

流量守恒与车辆指派约束为

式(2)和式(3)表示进入与离开路网的所有节点与场站(不包括拖车停放点)的卡车连线必为1；式(4)和式(5)表示卡车进入与离开拖车停放点的次数至少为1次，至多2次；式(6)和式(7)表示以整车进行服务的节点也可以由卡车进行服务，因此进入与离开整车客户点的拖车连线可能为0，至多为1；式(8)表示1辆卡车或1辆拖车最多从场站离开1次；式(9)表示进出节点的卡车连线数守恒，进出节点的拖车连线数守恒.

车辆载重约束为

式(10)表示整车的载重约束，其中整车载重上限为卡车与拖车载重之和；式(11)表示卡车的载重约束.

变量约束为

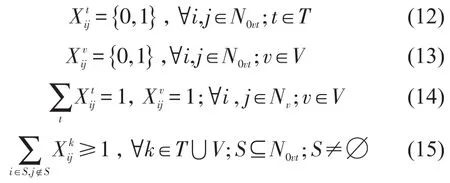
式(12)和式(13)约束卡车与拖车的变量取值为0或1；式(14)表示若路径上拖车变量取值为1，则卡车变量取值必为1；式(15)表示所有整车路径须避免子回路，即整车路径须经场站1次.

车辆行进过程中时间传递约束为

式(16)表示卡车行驶路径的时间传递，其中路径时间为卡车行驶时间；式(17)表示卡车服务路径的车辆顺序约束，其中拖车停放点并未停放拖车；式(18)表示卡车服务路径的车辆顺序约束，其中拖车停放点被选择停放拖车；式(19)表示整车服务路径的时间传递；式(20)表示整车服务路径的车辆顺序约束，其中拖车停放点并未停放拖车；式(21)表示整车服务路径的车辆顺序约束，其中拖车停放点被选择停放拖车.

时间窗约束为

式(22)表示抵达各节点的时间须小于时间窗上限.

节点时间约束为

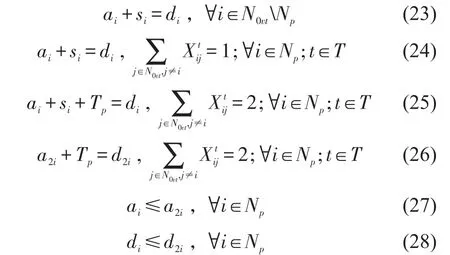
式(23)表示抵达节点的时间加服务时间等于离开该节点时间(节点不包含拖车停放点)；式(24)表示若拖车停放点未被停放拖车，则抵达时间加服务时间等于离开时间；式(25)和式(26)表示若拖车停放点被停放拖车，则卡车将进入与离开此节点2次，即此节点会有2种抵达与离开时间，式(25)表示第1次抵达时间加服务时间加拆卸拖车时间等于第1次离开该节点时间，式(26)表示卡车子路径结束后第2次返回拖车停放点，此时第2次抵达时间加连接拖车时间等于第2次离开该节点时间；式(27)和式(28)约束了2次抵达与离开时间的顺序.

3 两阶段混合启发式算法设计

算法包括构建起始路径与改善路径2个部分，架构如图3所示.

3.1 构建起始路径

(1)构建整车路径.

采用2种策略构建整车路径.

策略A加大车辆抵达客户点的时间与客户时间窗的差距，计算式如式(29)所，其中，M与P均为固定的常数.计算整车客户插入现有路径[1]中的时间，同时考虑由场站指派新车的可能性，比较插入时间与形成新路径的时间，选择时间最少的方案.

图3 算法架构图Fig.3 Illustration of the algorithm

策略B预留卡车子路径中的车容量，将整车起始路径的车容量上限设为式(30)(R：0.5～1.0).每辆整车选择距离场站最远的客户作为路径的种子点，其余整车客户比较插入现有路径中的时间，选择时间最少的客户插入路径中，直至超过车容量上限，或违反客户时间窗限制，由场站指派新车进行服务.

(2)构建卡车子路径.

由于场站及整车路径中的所有拖车停放点均可作为卡车子路径的起点，因此须计算卡车客户连接到拖车停放点形成新的子路径的时间，以及卡车客户插入现有卡车子路径的时间，选择时间最少的位置插入卡车客户形成子路径.

(3)构建卡车路径

类似地，运用A、B策略构建卡车路径.

3.2 改善路径

运用不同方式获得新路径，若其满足车容量及时间窗约束，则计算改善时间成本(若路径为卡车，则成本记为Ct；若为整车，则记为Cv).

3.2.1 路径内改善交换

(1)路径内Or-opt节点交换.

整车路径内为

卡车路径内为

路径内Or-opt节点交换示意图如图4所示.

图4 路径内Or-opt节点交换示意图Fig.4 The Or-opt node switching of one route

(2)路径内2-opt节点交换.

整车路径内为

卡车路径内为

路径内2-opt节点交换示意图如图5所示.

图5 路径内2-opt节点交换示意图Fig.5 The 2-opt node switching of one route

3.2.2 路径间改善交换

(1)同种路径间1-0节点插入.

整车路径间为

整车路径间1-0节点插入示意图如图6所示.

卡车子路径间为

卡车子路径间1-0节点插入示意图如图7所示.

卡车路径间为

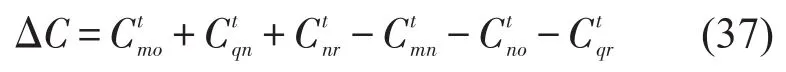
卡车路径间1-0节点插入示意图如图8所示.

(2)同种路径间1-1节点交换.

整车路径间为

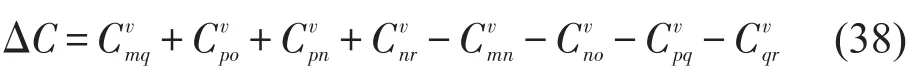
整车路径间1-1节点交换示意图如图9所示.

卡车子路径间为

卡车子路径间1-1节点交换示意图如图10所示.

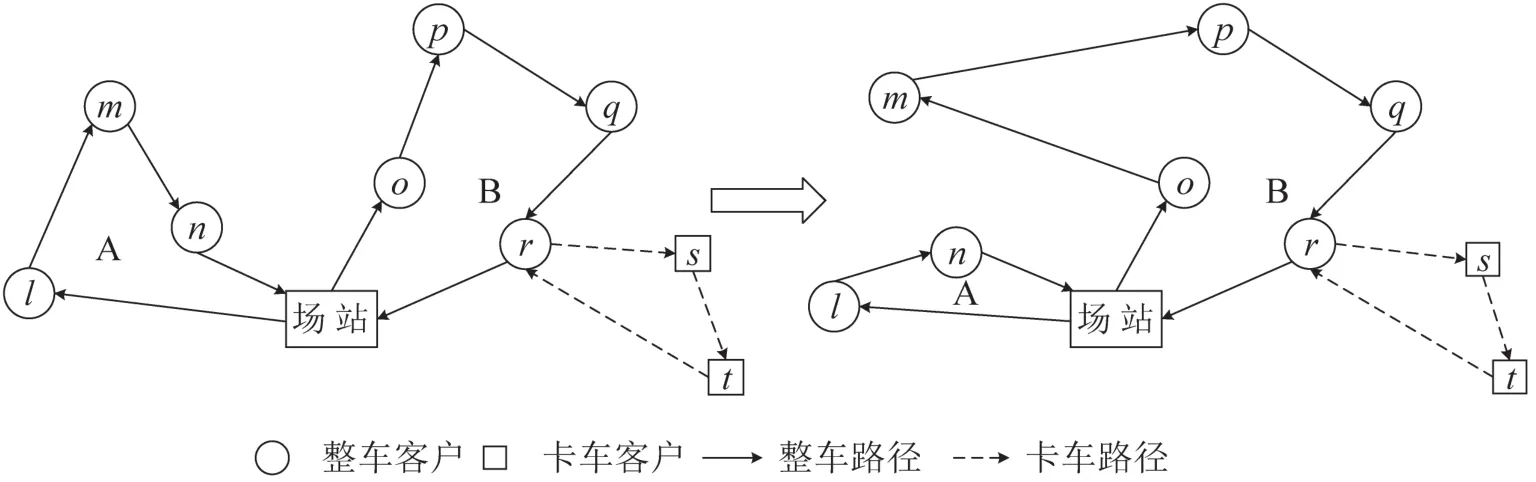
图6 整车路径间1-0节点插入示意图Fig.6 The 1-0 node insert between vehicle routes

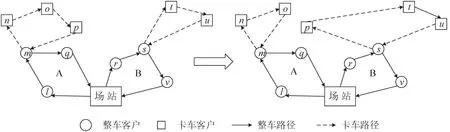
图7 卡车子路径间1-0节点插入示意图Fig.7 The 1-0 node insert between truck sub-routes

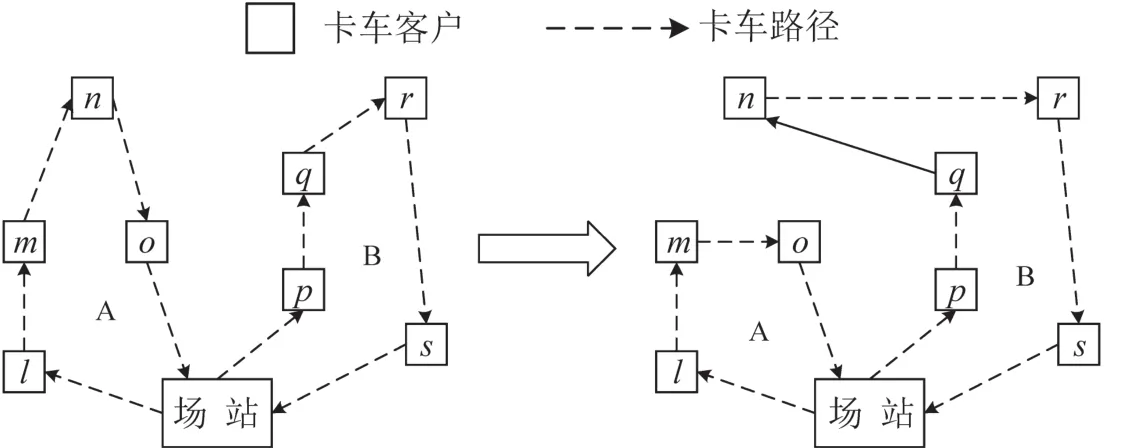
图8 卡车路径间1-0节点插入示意图Fig.8 The 1-0 node insert between truck routes

图9 整车路径间1-1节点交换示意图Fig.9 The 1-1 node switching between vehicle routes

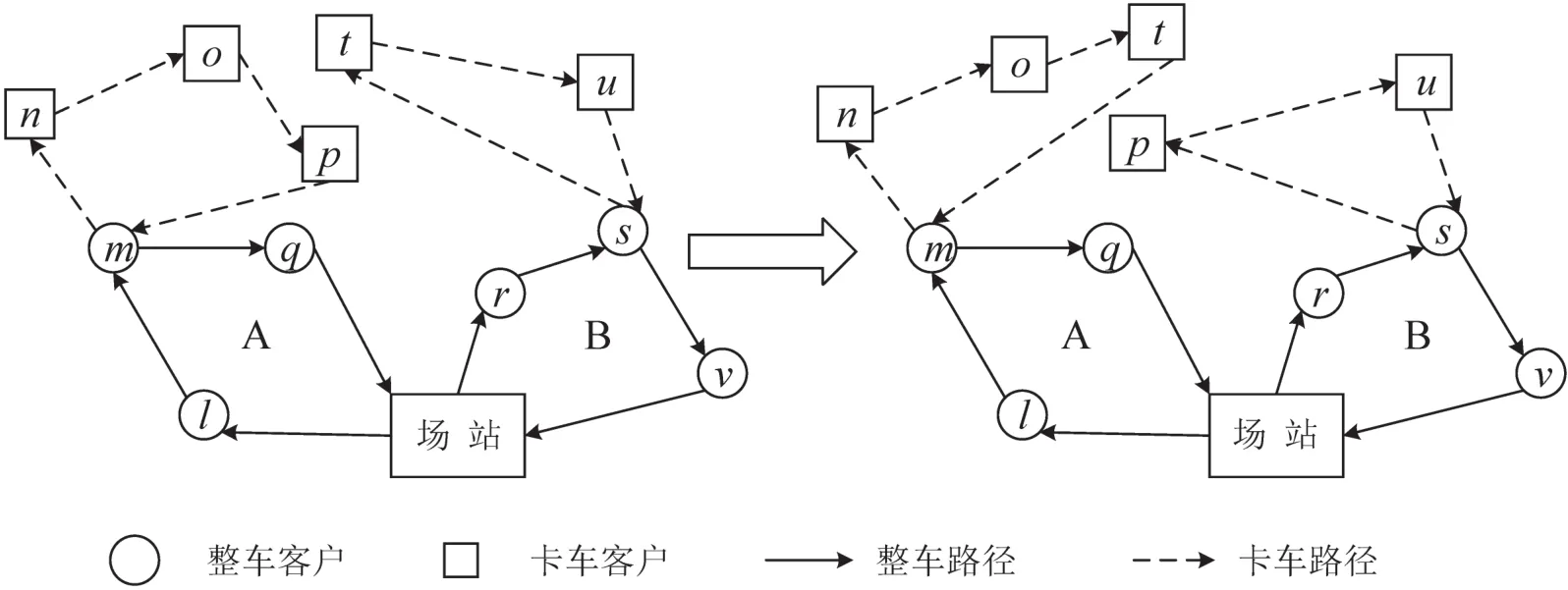
图10 卡车子路径间1-1节点交换示意图Fig.10 The 1-1 node switching between truck sub-routes

卡车路径间为

卡车路径间1-1节点交换示意图如图11所示.

图11 卡车路径间1-1节点交换示意图Fig.11 The 1-1 node switching between truck routes

(3)同种路径间2-opt路径交换.

整车路径间为

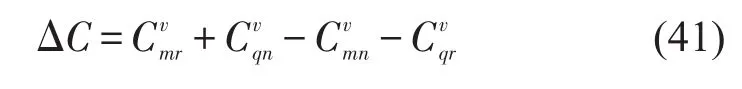
卡车路径间为

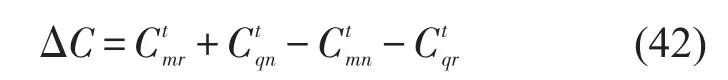
同种路径间2-opt路径交换示意图如图12所示.

图12 同种路径间2-opt路径交换示意图Fig.12 The 2-opt path switching between same routes

(4)异种路径间1-0节点插入.

整车—卡车路径间为

整车—卡车路径间1-0节点插入示意图如图13所示.

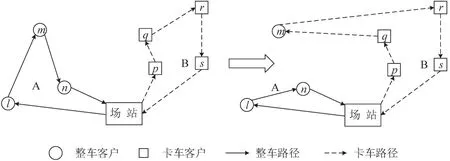
图13 整车—卡车路径间1-0节点插入示意图Fig.13 The 1-0 node insert between vehicle-truck routes

卡车—卡车子路径间为

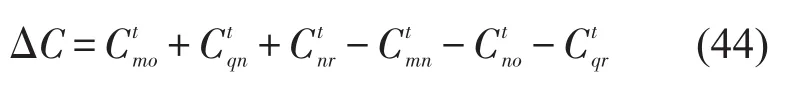
卡车—卡车子路径间1-0节点插入示意图如图14所示.

图14 卡车—卡车子路径间1-0节点插入示意图Fig.14 The 1-0 node insert between truck routes and truck sub-routes

(5)异种路径间1-1节点交换.

卡车—卡车子路径间为

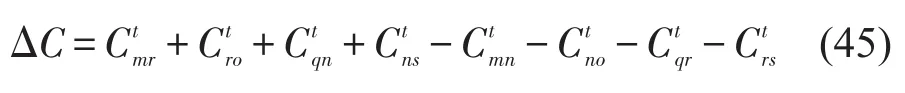
卡车—卡车子路径间1-1节点交换示意图如图15所示.

图15 卡车—卡车子路径间1-1节点交换示意图Fig.15 The 1-1 node switching between truck routes and truck sub-routes

3.2.3 拖车停放点交换

视原拖车停放点所在的卡车子路径为一闭合回路，移除该回路的1条连线，选择其他的插入后增加时间最少的拖车停放点重新相连.

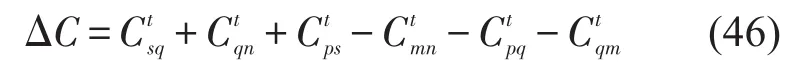
拖车停放点交换示意图如图16所示.

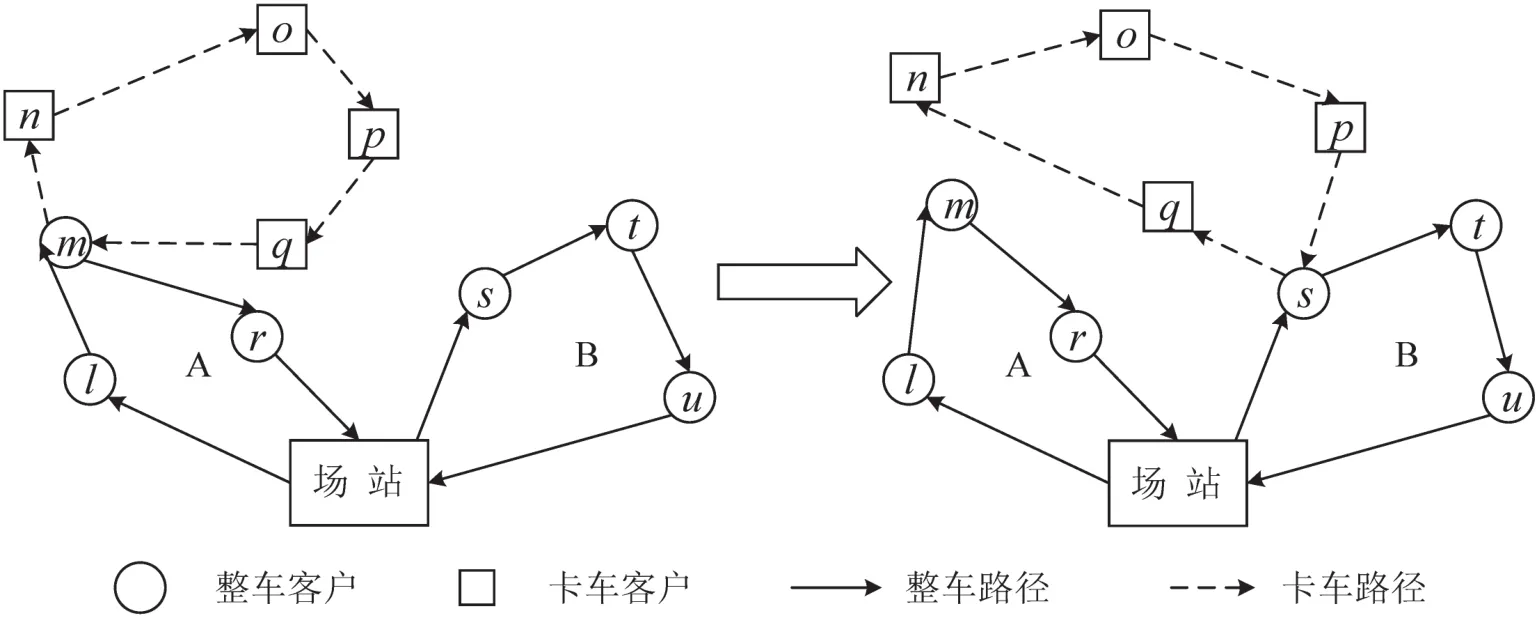
图16 拖车停放点交换示意图Fig.16 The parking dots switching of trailers

4 实验及结果分析

4.1 小规模实验

本研究以Solomon[7]的VRPTW实验作为基础，客户坐标与服务需求参考Baldacci等[8]，选择其中R1、C1、RC1具有100%时间窗约束的17例构建TTRPTW测试题库.以客户之间的直线距离代表卡车的行驶时间，整车行驶时间为该值的1.2倍，拆卸、组装拖车的时间均为30个时间单位.

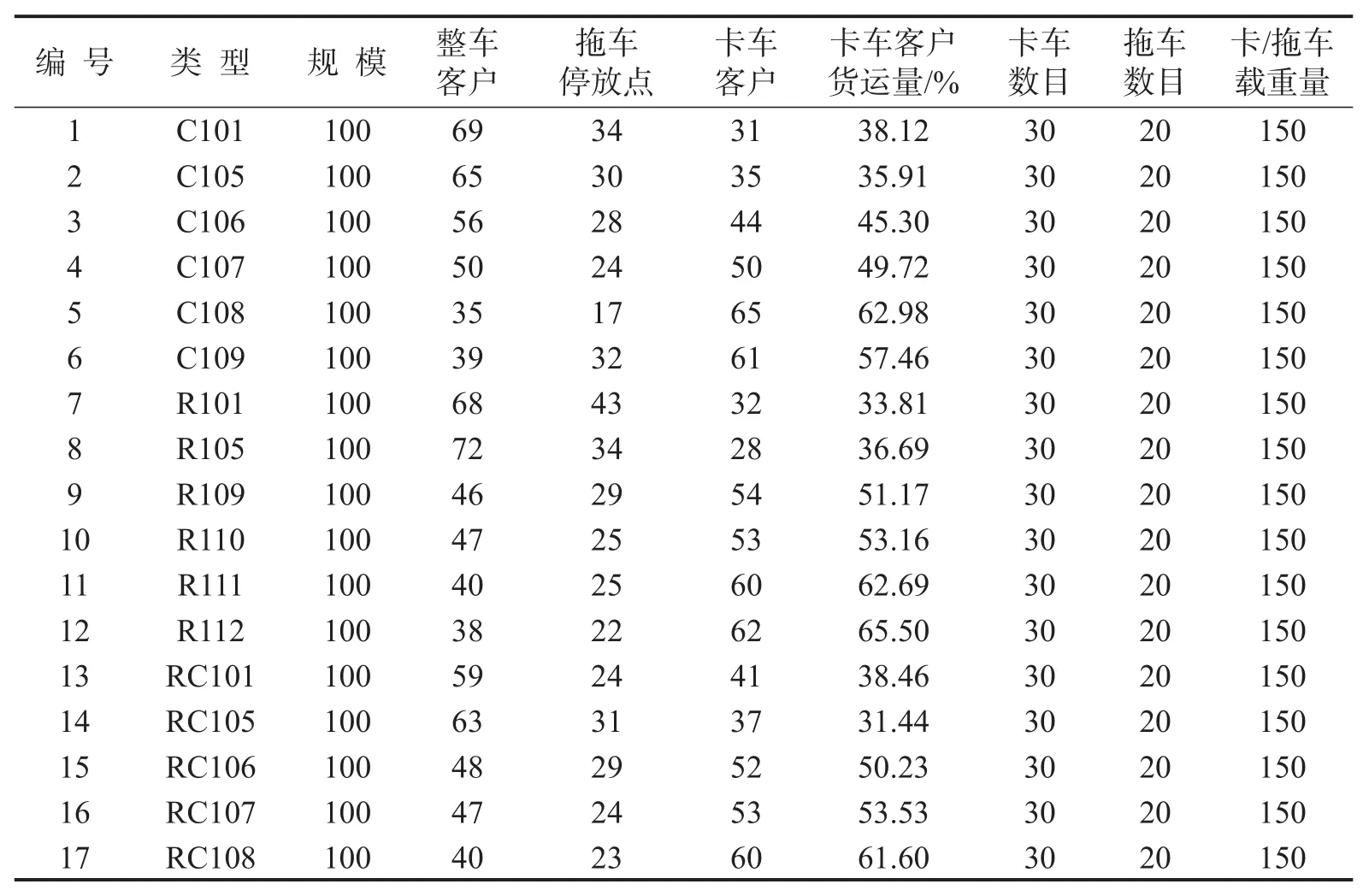
表1 小规模测试例列表Table 1 The case list of small scale experiments

运用Visual C++6.0进行算法编写，以Microsoft Visual Studio 2008进行编译，在计算机(Intel Core I5 CPU，4.0 GB memory，2.50 GHz)上运行.

求解结果如表2所示.针对每一小规模测试例，本文算法均可在3 s内求得结果.求解效率上，策略B的求解时间小于策略A，其中A的平均求解时间为2.04 s，B为1.77 s；运用策略A构建起始路径的时间成本较低，平均值为2 633.39，而B为2 773.66；运用策略A求解最优路径的时间也低于B，其中A的最优路径时间平均值为1 793.54，而B为1 829.72.

表2 小规模实验结果列表Table 2 The results of small scale experiments

4.2 大规模实验

为进一步测试本研究提出算法的有效性，设计了8组大规模测试例，如表3所示，其中客户数量为200～900，卡车与拖车的载重设为200.

同样运用2种策略分别进行求解，结果如表4所示.

表3 大规模测试例列表Table 3 The case list of large scale experiments

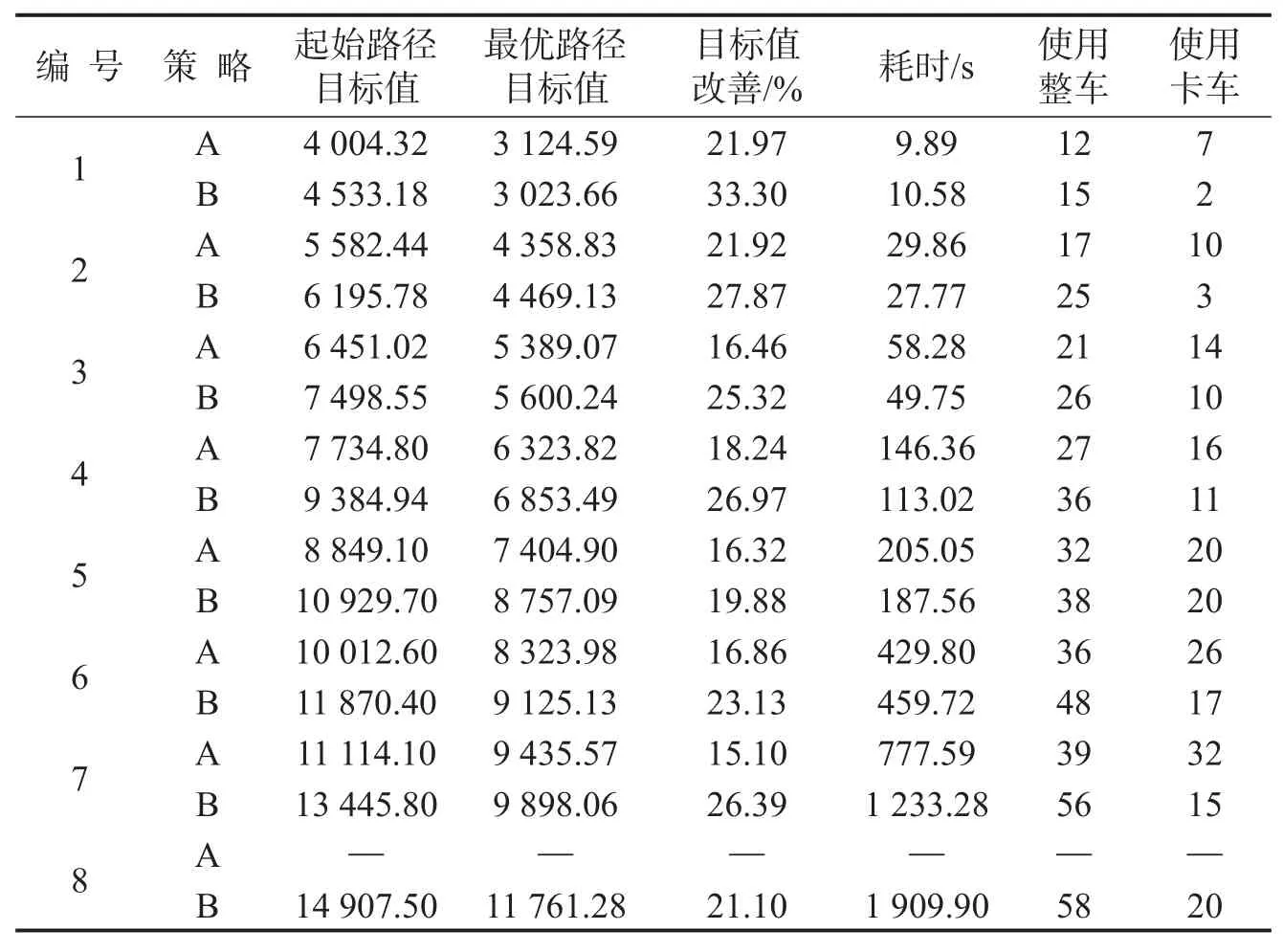
表4 大规模实验结果列表Table 4 The results of large scale experiments

由表4可以看出，当客户规模增至800时，由于内存限制运用策略A无法顺利求解；随着路网规模的扩大，2种策略下的求解耗时均呈现非线性大幅度增加的趋势，而策略A下求解耗时较短.在最优路径的目标时间成本方面，策略A较策略B的时间成本更低.针对每一测试例，2种策略下用车总数基本相同，而单独比较整车或卡车数量，策略A下需要整车运输的数量明显低于B，而卡车运输数量则相反，因此可根据实际行车需求权衡适当的指派组合.

综合上述不同规模的实验可知，针对小规模的路网问题，策略B的求解效率更高；而当路网规模扩大时，选择A可获得更高的求解效率.无论路网规模大小，运用策略A求得的最优路径目标值均低于B.

5 结论

本文针对TTRPTW问题，兼顾卡车与拖车2种车辆调度的特点，以最小化配送时间为目标建立模型，并开发了两阶段混合算法，以求得最优的车辆路径组合.实验均以实务为参照标准，结果表明运用本文模型与算法能够在0.5 h内求出大规模算例的满意解，且可根据企业实际选择适当的卡车、拖车数量组合，具有良好的可行性.

参考文献：

[1]CHAO I M.A tabu search method for the truck and trailer routing problem[J].Computers&Operations Research,2002,29(1):22-51.

[2]LIN S W.Solving the truck and trailer routing problem based on a simulated annealing heuristic[J].Computers&Operations Research,2009,36(5):1683-1692.

[3]VILLEGAS J G,PRINS C,PRODHON C,et al.A GRASP with evolutionary path relinking for the truck and trailer routing problem[J].Computers&Operations Research,2011,38(9):1319-1334.

[4]DERIGS U,PULLMANN M,VOGEL U.Truck and trailer routing problems-heuristics and computational experience[J].Computers&Operations Research,2013,40(2):536-546.

[5]李红启,卢越,朱晓宁.城际干线甩挂运输牵引车调度问题的模拟退火算法研究[J].交通运输工程与信息学报,2015,13(4):77-84,95.[LI H Q,LU Y,ZHU X N.A simulated annealing approach to the tractor dispatching problem of intercity dropping and pulling transport[J].Journal of Transportation Engineering and Information,2015,13(4):77-84,95.]

[6]李红启,赵文聪,李嫣然.时效要求下的甩挂牵引车调度问题与求解[J].交通运输工程学报,2016,16(5):95-102.[LI H Q,ZHAO W C,LI Y R.Trailer pick-up tractor routing problem with timeliness requirement and solving[J].Journal of Traffic and Transportation Engineering,2016,16(5):95-102.]

[7]SOLOMON M M.Algorithms for the vehicle routing and scheduling problems with time window constraints[J].Operations Research,1987,35(2):254-265.

[8]BALDACCI R,CHRISTOFIDES N,MINGOZZI A.An exact algorithm for the vehicle routing problem based on the set partitioning formulation with additional cuts[J].Mathematical Programming,2008,115(2):351-385.