基于交叉口重要度深度搜索的区域信号协调控制方法

路 婷，贝晓旭，刘桂云*

(1.宁波大学海运学院，浙江宁波315200；2.德国宇航中心(DLR)交通系统研究所,柏林12489，德国)

0 引言

随着经济的增长及城市规模的不断扩大，中国及其他发展中国家的机动车拥有量大幅增加，给城市交通控制系统带来严峻的挑战.据公安部道路交管局发布的消息，截止2017年6月，中国机动车保有量已经达到3.04亿，年增长率超过10%，超过百万汽车保有量的城市有52个，其中6个城市超过300万.这要求交通管理者不仅要关注点的效率的提升，提升路口的通行效率；同时也要从路网的角度来做均衡的调控，对整个路网的交通进行均衡疏导.因此，从整个路网的角度出发，研究路网内的交通运行规律，协调交通信号控制，提升交通控制的效率，是一个重要且亟待解决的问题.

对于路网交通信号协调优化和均衡疏导，研究人员多采用双层规划的方法，将信号控制参数优化和出行者路径选择结合，迭代优化，如Chiou的双层规划模型[1-2].考虑到路网中不同区域间的交通流可能存在较强的关联性，当采取某种控制策略后，拥堵有可能转移至相邻区域，Dahal设计了控制策略表和预测的相邻区域交通状况变化情况，提出了基于智能体协作的智能交通控制决策支持系统[3].Abu等考虑了交叉口信号控制与路段交通流的相互影响，建立了轻度拥堵情况下的路网输出量约束[4].Daganzo等研究了均质路网内宏观基本图与信号控制的关系，发现信号控制能够均衡路网内交通负荷，使得宏观基本图中平均流量临界值最大[5].Keyvan等根据宏观基本图所展示的交通流演化模型设计了边界门控制算法，当预计区域交通流密度超过临界密度阈值时启动门控制，限制从边界驶入拥挤区域的车辆数[6].Yan等提出异质路网内车辆密度的分布越均匀路网通行能力越大，设计了自适应信号控制规则来均衡交叉口4个交口方向的排队长度，并用迭代学习控制理论来实现控制方案与交通环境的交互[7].

由于路网信号控制涉及大规模路网单元上的交通流的动态传播和控制，这些优化控制方法都在一定程度上被证实可以改进交通控制效益，但也存在一些缺陷，例如信号控制方案无法主动引导交通状态的演变，无法避免交通流陷入拥堵状态.另外，优化结果的可靠性和鲁棒性与优化时间有很大的正相关性，尤其是在处理大型路网时，优化结果常常限于局部最优解，优化时间过慢而无法用于实时信号优化控制策略.鉴于此，本文的研究试图从路网拓扑结构入手，分析交叉口(节点)之间的相互影响关系，确定能够表征交叉口节点相互影响的交通流参数，建立以拓扑结构为基础的交叉口重要度估计模型，进而以交叉口重要度排序得到的信号协调优先顺序为依据，从全局的角度建立一种均衡疏导路网交通流的信号协调控制方法.

1 模型与方法

路网拓扑结构是指交叉口在路网中的位置及交叉口内在组成方式所决定的结构特征属性.国内外研究者主要通过建立交叉口关联度模型分析交叉口之前的相互作用关系.交叉口关联首先是指物理关联特征，即道路交叉口的网络拓扑形式，如交叉口间的距离是否相邻等；其次是指交通关联特征，即连线或节点间的交通流参数的关联程度.

1.1 交叉口重要度估计

对于单个交叉口，饱和度最高，亦或是流量最大，亦或是车道数最多的交叉口往往被认为是最关键的交叉口.然而，这种简单的贪婪算法只能反映交叉口本身的交通状况，而不能反映它和其他交叉口之间的相互影响及它在整个路网内重要程度.由交通拥堵的时空传递现象可知，交叉口的重要度不仅与其本身重要度有关，还应该与其相邻交叉口的数量及重要度有关，此特征的研究在Saeedmanesh[8]的文章中也被证实.因此，首先要定义1个交叉口重要度指数，该指数将沿道路随交通流传递.

基于此思想，令r表示交叉口的重要度指数；b表示相邻交叉口重要度之间的关联性；ri和rj表示交叉口i和j的重要度指数；Ui表示交叉口i的上游交叉口的集合；bij表示交叉口j的重要度对交叉口i的重要度的关联性.由分析可知，交叉口i的重要度可以表示为其所有的相邻上游交叉口的重要度(rj,j∈Ui)与其作用于交叉口i的重要度的关联性的乘积之和，即

若路网中有n个交叉口，则构成1个n维方程组，该方程组的解就是交叉口的重要度值.ri也可以理解为某个交叉口具有某优先顺序的概率.写成矩阵乘积的形式为

这里交叉口重要度关联性构成1个n×n的矩阵B，交叉口重要度指数构成1个的非零列向量R.若交叉口i和交叉口j是相邻交叉口且有交通流从j运动到i，那么矩阵的第i行第j列的元素是bij＞0；若交叉口i和交叉口j不是相邻交叉口或者没有交通流从j运动到i，那么bij=0.此外，应该注意到相邻交叉口的重要度的关联性与交叉口之间的距离有关，若交叉口之间的距离过大，那么它们被认为不具有连通性.因此，设置1个距离临界值，若交叉口i和交叉口j之间的距离大于该临界值，其对应的关联性矩阵元素值为0，即bij=0，bji=0.矩阵B的主对角线的元素是0，且矩阵B是奇异矩阵.

道路饱和度，即交通量和道路通行能力之比，是反映道路拥堵状况的重要参数之一，越是拥堵的路段应该越早被疏散，以免造成大面积交通瘫痪.因此，我们用道路饱和度作为矩阵B的元素值，反映交叉口之间的关联性.虽然交通流量也可反映交叉口和交叉口之间交通流的运动状况，但是，经过试验发现以交通流量作为关联度矩阵的元素而求得的重要度排序结果并不能产生最优的控制效益指标.如果路段有多条车道且不同的车道由不同的信号相位控制，以各车道的饱和度之和作为该路段的饱和度，即

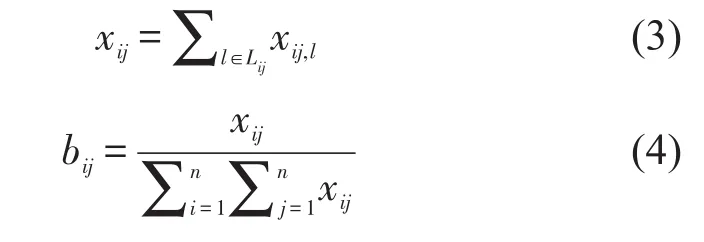
式中：Lij表示从交叉口j到交叉口i的车道集合；xij,l表示车道l的饱和度，其中l∈Lij；xij表示从交叉口j到交叉口i的路段的饱和度.

由于关联性矩阵B是1个奇异矩阵，所以，用其主特征向量作为R的求解结果.主特征向量可用乘幂法(Power Method)得到，乘幂法的求解过程如下：

(1)选择1个初始向量R()0，设k=0；

(3)设置一个最小值ε，并重复运算第(2)步求解R()k+1和R()k，直到两者之差的绝对值小于该最小值，即，在本文的算例中，ε被设为10-7；

(4)第(3)步中求得的向量R()k即是主特征向量的近似值，R*=R()k.

乘幂法在只有一个主特征值的情况下是有效的.主特征向量R*的元素值即是交叉口的重要度指数值，对其进行降序排序，便得到了交叉口信号优化顺序.若主特征向量的所有元素都为负值，先进行归一化运算再排序.初始向量R(0)对于收敛结果无影响，因此，可以假定所有交叉口具有相同重要度指数，即

1.2 信号协调控制方法

经过1.1节的计算，整个路网可以用一个节点具有优先属性的有向图表示，即路网拓扑结构图，如图1所示.图1(a)是路网构成，其中交叉口3、5、8是无信号交叉口，其他交叉口是信号交叉口.交叉口之间的路段长0.4 km，假设相邻交叉口连通性的临界距离是0.8 km，则该路网的拓扑结构图如图1(b)所示.图1(b)中，节点数字代表对应信号交叉口按重要度的排序值，1表示该交叉口的重要度最高，优先顺序为1，以此类推.

图1 示例路网及其有向图Fig.1 Example road network configuration and its topological graph

深度优先搜索算法(Depth-First-Search，DFS)是图论中的经典算法，是一种用于遍历或搜索树或图的算法.沿着树的深度遍历树的节点，当节点所在边都已被探寻过，搜索将回溯到发现节点的那条边的起始节点，这一过程一直进行到已发现从源节点可达的所有节点为止，如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止.本文中的信号协调方法利用深度优先搜索算法的思想，从最重要的交叉口开始，对当前交叉口和其相邻交叉口进行协调优化，直至所有的交叉口都被优化完毕.若有多个控制区域，则先对区域内的交叉口进行协调优化，再优化相邻区域的边界交叉口的信号.在信号优化时，首先，要确定控制区域的公共周期；其次，利用等饱和度模型等计算信号交叉口各相位的绿灯时长；最后，协调相邻交叉口确定最佳相位差，具体步骤如下：

Step 1搜索优先顺序为k()1≤k≤n的节点，n是有向图中节点的总数，此时的目标搜索节点，用Ik表示，在有向图找到该节点的相邻节点中未被协调的节点，按照未被协调的相邻节点的重要度排序依序协调这些相邻节点与目标搜索节点，求解每一对协调交叉口的最佳相对相位差，并转换为最佳绝对相位差.在这个过程中可能出现的情况有：

(1)目标搜索节点的相位差未被优化确定，也就是说目标搜索节点之前未与任何节点进行协调控制.这种条件下，有3种可能的情况：

①该目标搜索节点的所有相邻节点Uk，它们的相位差都未被优化确定，那么，令目标搜索节点的相位差为0，即φk=0，按照相邻节点的优先顺序依次协调交叉口对，求得它们的最佳相对相位差φk,j,j∈Uk，再求得所有相邻节点的最佳绝对相位差φj，φj=φk,j+φk.

②该目标搜索节点的所有相邻节点的相位差已被优化确定，那么，找到这些已被协调的相邻节点中优先顺序最高的节点(假设节点m)，协调该节点Im与目标搜索节点Ik，求得它们的最佳相对相位差是φk,m，再求得目标搜索节点的绝对最佳相位差φk，φk=φm-φk,m.

③该搜索节点的部分相邻节点的相位差已被优化确定，部分相邻节点的相位差未被优化确定，那么，先根据步骤②的方法求出目标搜索节点的最佳相位差，再根据步骤①的方法协调目标搜索节点和其未被协调的相邻节点，求得相邻节点的最佳相位差.

(2)目标搜索节点的相位差已被优化确定，也就是说目标搜索节点之前已经与某一节点进行协调控制.这种条件下，也有3种情况：

①该目标搜索节点的所有相邻节点的相位差都未被优化确定，那么，协调该目标搜索节点Ik与其相邻节点j(j∈Uk)，求得它们的最佳相对相位差是φk,j，根据φj=φk,j+φk，求得相邻节点的最佳绝对相位是φj.

②该搜索节点的所有相邻节点的相位差已被优化确定，说明该目标节点无需再被协调，那么，将优先顺序加1，更新目标节点到下一优先顺序k+1，重复Step1.

③该搜索节点的部分相邻节点的相位差已被优化确定，部分相邻节点的相位差未被优化确定，那么，根据步骤(2)中①的方法协调目标搜索节点和其未被协调的相邻节点，求得相邻节点的最佳相位差.

Step 2重复Step1的搜索与计算直至所有交叉口都被协调并求得最佳相位差.整个信号协调过程如流程图2所示.

以图1路网为例，交叉口4的优先顺序是1，则它的相位差为0，与其相邻交叉口的优先顺序分别是2、3、4和6.那么，协调优先顺序为1的交叉口I1和优先顺序为2的交叉口I2，得到I2的最佳相位差φ2，如图3(a)所示；协调I1和优先顺序为3的交叉口I3，得到I3的最佳相位差φ3，如图3(b)所示；协调I1和优先顺序为4的交叉口I4，得到I4的最佳相位差φ4，如图3(c)所示；协调I1和优先顺序为6的交叉口I6，得到I6的最佳相位差φ6，如图3(d).此时，I1的所有相邻交叉口都已求得了最佳相位差.找到优先顺序为2的交叉口I2，此时I2是目标搜索节点.由于I2及其相邻节点都已经有最佳相位差，因此，优先顺序加1，更新目标搜索节点为优先顺序为3的交叉口I3.此节点已有最佳相位差，判断其相邻节点I1、I2、I5，其中I1和I2最佳相位差已确定，I5的最佳相位差未确定，那么，协调I3和I5，求得I5的最佳相位差φ5，如图3(e)所示.图中粗虚线代表即将要协调的路段，粗实线代表已经协调的路段.

图2 信号协调控制流程图Fig.2 Signal coordination control flow chart

图3 示例路网的信号协调过程Fig.3 Traffic signal coordination process of example road network

2 案例研究

基于上述研究成果，本文以德国Braunschweig市的部分交叉口为实验对象，在Matlab中编程重要度估计模型和信号协调控制算法，在仿真软件Simulation of Urban MObility(SUMO)中搭建路网并仿真，对比分析本文方法的有效性.

2.1 路网构成

实验路网由沿Sackring到Frankfurter Strasse的9个信号交叉口组成，如图4所示.

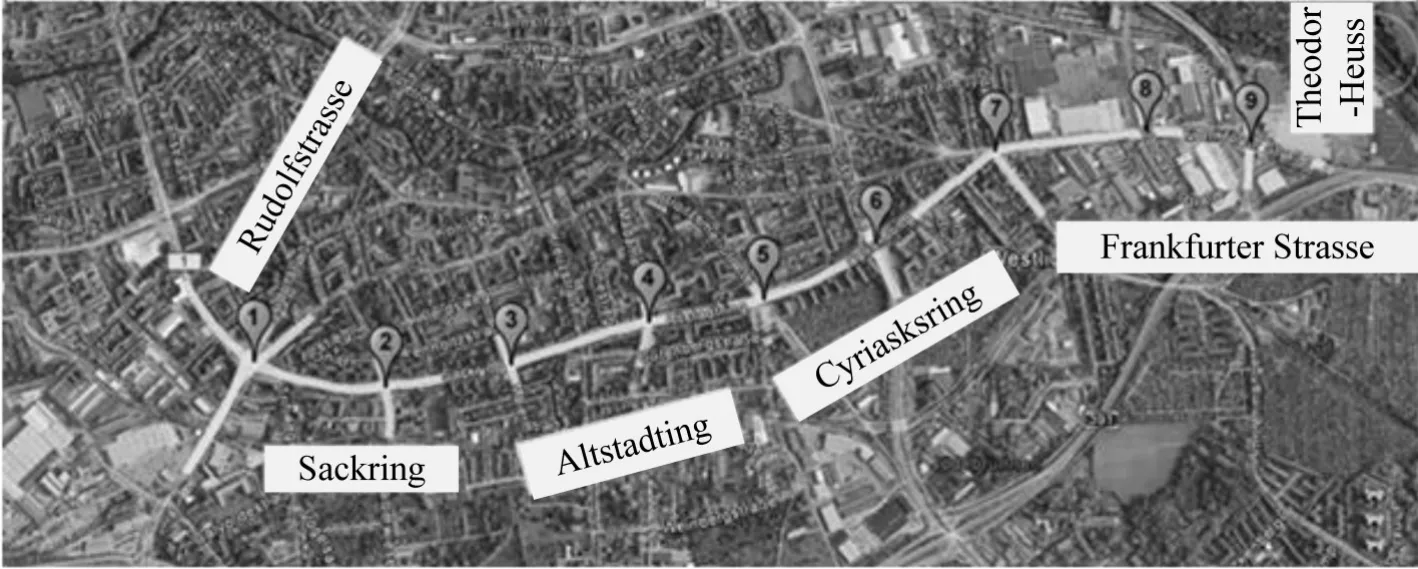
图4 实验路网Fig.4 Test road network

图4路网中交叉口的信号相位相序来自于信号机公司西门子的报告，如图5所示.每个相位的最小绿灯时间是6 s，损失时间是4 s.

2.2 仿真结果

我们仿真了1天中6:00-20:00的交通流运行情况，信号配时方案每30 min优化1次.首先，根据交叉口重要度估计模型求解出交叉口的重要度，并对其排序得到交叉口的优先顺序.由结果可知，优先顺序在不同的日期大体相似，第1位优先顺序几乎总是出现在交叉口4，第2位和第3位优先顺序总是出现在交叉口5和交叉口6，第4位优先顺序总是出现在交叉口3，第5、6位优先顺序大部分时间出现在交叉口7和交叉口2，最后两位优先顺序总是出现在交叉口8和9.根据信号协调控制方法，优先顺序越前的交叉口在协调时越具有优势，也就是说交叉口4、5、6具有更加重要的决定作用，尤其是交叉口4.由以上结果也可看出，越是处在中心位置的交叉口具有越高的优先顺序.

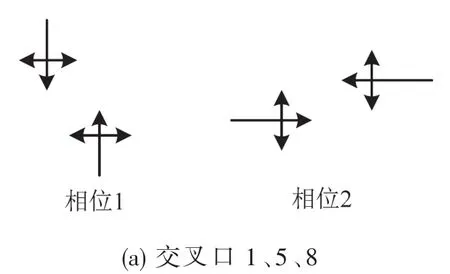
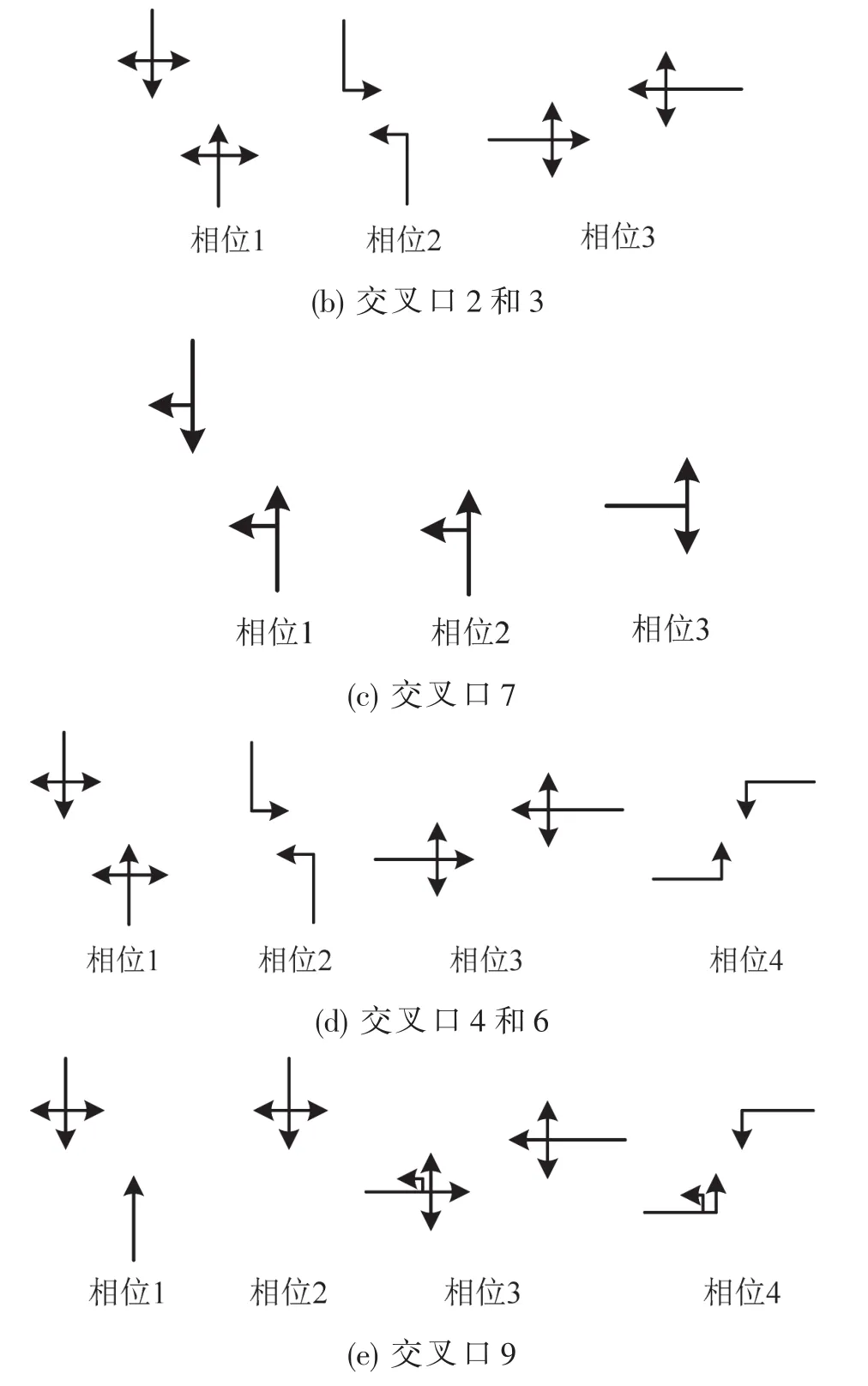
图5 实验路网内交叉口的信号相位Fig.5 Phase configuration of intersections in test network

其次，在SUMO中仿真本文的协调控制方法优化出的信号配时方案和Synchro 7优化后的信号配时方案，并以车均延误作为效益评价指标，其结果如图6所示.由图6可知，在2种方法下，车均延误的趋势具有相似性，且本文方法优化的信号配时方案下的车均延误在所有时间都是最小的.与Synchro7优化的信号配时方案相比，车均延误最少减少2.1%，最多减少达20.8%，平均减少11.9%.

图6 不同方法下的车均延误Fig.6 Mean delay per vehicle by different methods

3 结论

随着城市路网规模的不断扩大，从路网的角度研究交通运行规律特征，对整个路网的交通流均衡疏导是一个趋势.本文分析了交叉口之间的交通关联性和路网拓扑结构，建立了交叉口重要度估计模型，并基于有向深度搜索算法设计了区域信号协调优化方法.最后，以Braunschweig的交叉口作为实验路网，通过微观仿真对所提出的信号协调控制方法进行效益评价，仿真结果证明本文提出的方法有效地改进了交通控制效益.

参考文献：

[1]CHIOU S W.An efficient algorithm for optimal design of area traffic control with network flows[J].Applied Mathematical Modelling,2009,33(6):2710-2722.

[2]CHIOU S W.Joint optimization for area traffic control and network flow[J].Computers&Operations Research,2005,32(11):2821-2841.

[3]KESHAV DAHAL,KHALED ALMEJALLI,ALAMGIR HOSSAIN M.Decision support for coordinated road traffic control actions[J].Decision Support Systems,2013,54(2):962-975.

[4]ABU-LEBDEH G,CHEN H,BENEKOHAL R F.Modeling traffic output for design of dynamic multicycle control in congested conditions[J].Journal of Intelligent Transportation Systems,2007,11(1):25-40.

[5]DAGANZO C F,GEROLIMINIS N.An analytical approximation for the macroscopic fundamental diagram of urban traffic[J].Transportation Research Part B:Methodological,2008,42(9):771-781.

[6]KEYVANEKBATANI M,PAPAGEORGIOUM,PAPAMICHAIL I.Urban congestion gating control based on reduced operational network fundamental diagrams[J].Transportation Research Part C:Emerging Technologies,2013(33):74-87.

[7]YAN F,TIAN F,SHI Z.An extended signal control strategy for urban network traffic flow[J].Physica A:Statistical Mechanics and its Applications,2016(445):117-127.

[8]MOHAMMADREZA SAEEDMANESH,NIKOLAS GEROLIMINIS.Clustering of heterogeneous networks with directional flows based on“Snake”similarities[J].Transportation Research Part B:Methodological,2016(91):250-269.