混合气体的临界温度计算

李红娟，苗 鹏，倪福鑫

(青岛伊科思技术工程有限公司，山东 青岛 266042)

混合物临界性质的计算与预测不但有重要的理论意义而且有重要的应用价值。传统的混合物临界性质计算与预测模型或是求解过程非常复杂，或是基于经验关联方法，计算过程繁琐且计算精确度不高。本文介绍了无交互作用参数法、固定交互作用参数法、基于外延拓展性质法、基于基团贡献法四种混合气体计算方法的计算方程式以及运算规则。并分别采用四种计算方法计算含不同甲烷浓度混合气体的临界温度，并与实验值对比，最终寻找出混合气体临界温度计算的最佳计算规则。

1 混合气体临界温度计算规则

1.1 无交互作用参数的方法(WIP)

1.1.1 摩尔分数权重法

这是最常见的、在需要快速得到误差在允许范围内结果的情况下使用下式计算：

Tc=Xi×Tci

1.1.2 体积分数权重法[1]

此方法也属于无交互作用的方法范围，与上一方法相比是以临界摩尔体积作为基础进行的计算：

1.2 固定交互作用参数的方法(FIP)

为了更精确的计算混合物的临界温度，固定交互作用参数的方法应运而生。其中Chueh-Prausnitz法[2]和Grieves-Thodos法[3]是应用最广的两种，当然后人对CP方法有一系列改进。

1.2.1 Chueh-Prausnitz method(CP)

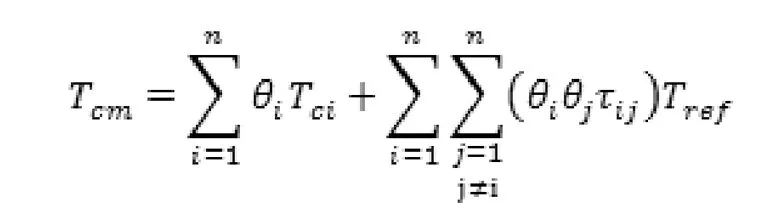
其中，Tref为基准温度，假定Tref=1K，并且假定式中的二元交互参数τij=τji，τii=0。

对于二元体系而言，Chueh-Prausnitz方程简化为：

Tcm=θ1Tc1+θ2Tc2+2θ1θ2τ12

其中CO2+CH4体系的τ12=12.2984。

1.2.2 Grieves-Thodos method(GT)

Grieves-Thodos方程如下式：

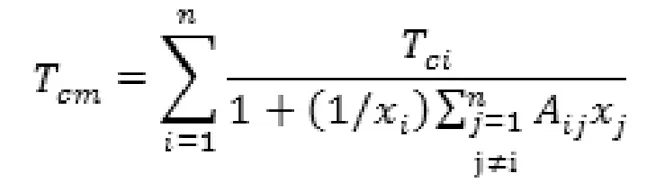
其中CO2+CH4是二元交互作用参数，对于二元体系，方程简化为：

其中CO2+CH4体系的二元交互作用参数通过文献[4]计算得到：A12=0.7441,A21=1.123。

1.3 基于外延拓展性质的方法(EP)

与无交互作用的方法和固定交互作用的方法相比，计算更为复杂，所调用的参数更多，应用的范围也更加广泛。主要有两种Redlich-Kister法[5-6]和改进的Wilson法[7-8]。

1.3.1 Redlich-Kister method(RK)

Redlich-Kister方程如下所示：

其中E(m)为混合效果项，k为此方程的拓展项数目。对于二元体系，方程简化为：

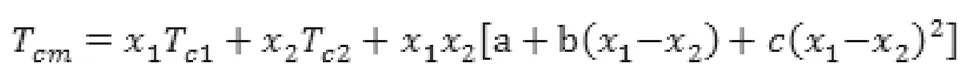
其中CO2+CH4体系的二元交互作用参数通过文献[2-3]计算得到：a=20.0218,b=38.6335,c=66.8412。

1.3.2 Modified Wilson method(MW)

Modified Wilson方程是在总结前人规律的基础上演化而来，在极限值xi=1和xi=0的情况下MW方程演化为拉乌尔定律和亨利定律。MW方程如下：

其中，Aij是同其他方法一样需要通过实验值计算得来的二元交互参数，Tref为基准温度，假定Tref=1K。

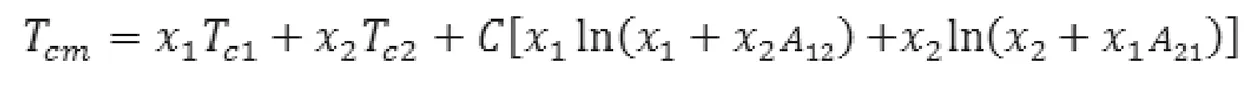
其中CO2+CH4体系的二元交互作用参数[2,6]A12=0.4980，A21=1.655，C为常数，C=-2500。

1.4 基于基团贡献的方法(GCT)

Li在文献[9]中使用基团贡献法对22种碳氢化合物之间、13种碳氢化合物和极性化合物之间、8种碳氢化合物和二氧化碳之间的二元交互作用进行了研究。Klincewicz等将物质的临界性质与物质本身的官能团贡献联系起来，比如：

其中，qA是与上述三公式对应的官能团贡献值。Tb是沸点，MW是物质的分子量。Tc、pc、Vc分别表示物质的临界温度、临界压力和临界摩尔体积，单位分别是K、bar和cc/gmol。对于混合物A+B而言，混合物对于临界性质的官能团贡献值qAB如下式：

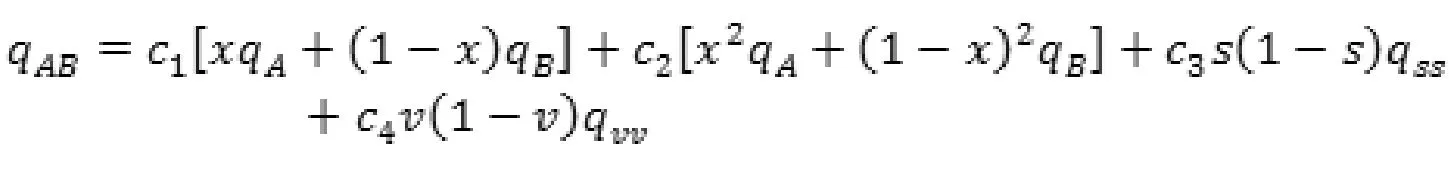
其中，x是物质A的摩尔分数，c1、c2、c3、c4分别为常数项系数，由文献值可知分别为0.5、0.5、3.0、-2.0。

上式中：

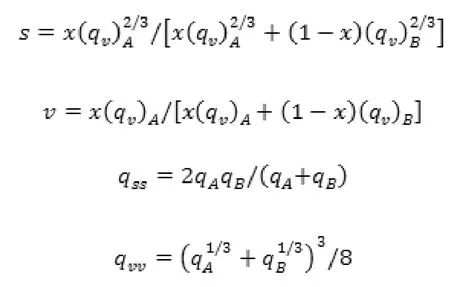
其中，(qv)A和(qv)B分别表示A和B的摩尔体积增加值。

混合物的沸点计算为：

Tbm=s(Tb)A+(1-s)(Tb)B

其中，(Tb)A和(Tb)B分别表示A和B的沸点。

混合物的Tcm由下式计算：

(Tb/Tc)m=0.567+qAB-qAB2

2 计算结果和讨论

通过上述几种混合物的临界温度计算规则进行计算，数据[10]如表1所示。

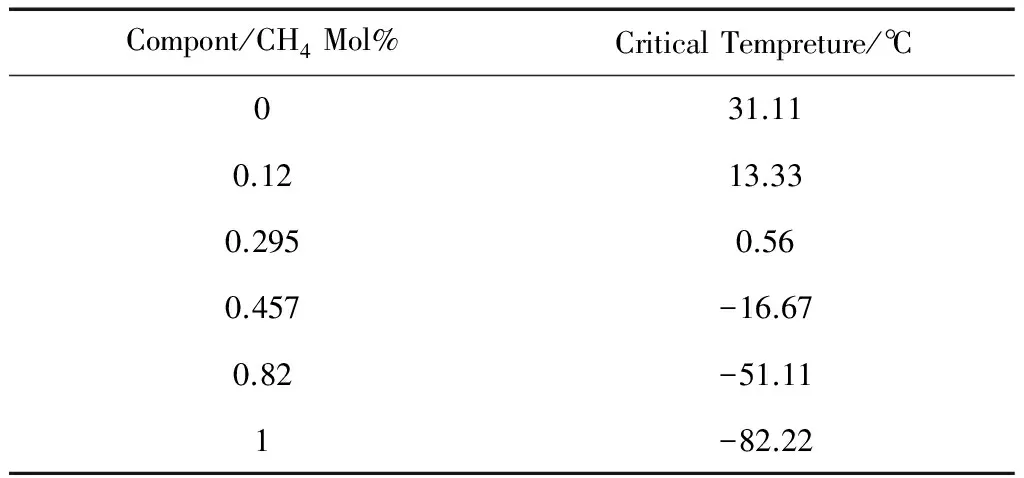
表1 不同浓度甲烷混合气的临界温度计算值

依据不同的混合物临界温度计算规则得到如图1结果。

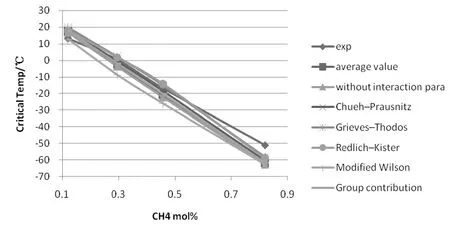
图1 不同计算规则所得临界温度值随甲烷浓度变化曲线

从图1可以得出：

(1)各混合规则对临界温度的计算值与文献值相比偏差不大。

(2)各混合规则对临界温度的计算值之间偏差较小。

(3)随着甲烷含量的增加，混合气体的临界温度偏差变大。

(4)在混合气体中甲烷含量较高时GT和RK计算规则得出的结果较为接近实验数据。

发酵沼气过程中的混合气体组成大致为甲烷55%，二氧化碳38%和水分7%。考虑到除去水分之后，甲烷的含量大约在60%，经过GT和RK计算可知此时混合气体的临界温度为-31.2℃和-29.3℃。在此温度之上对混合气体进行压缩，混合气体是不会液化的。如果经过初步的提纯净化至甲烷含量在80%，依据GT和RK计算规则可得混合气体的临界温度为-55.6℃和-56.6℃。

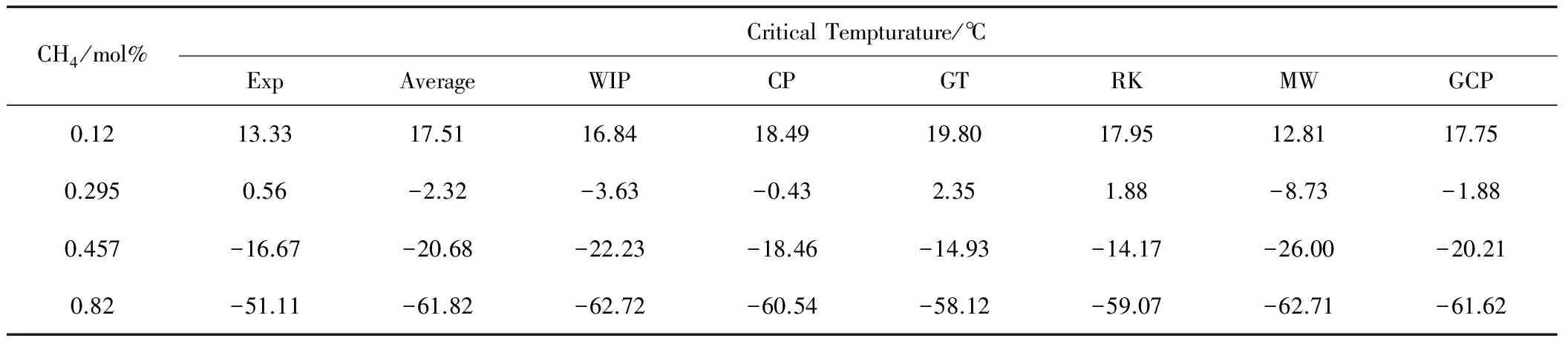
表2 临界温度对应值列表

[1]Li C C. Critical temperature estimation for simple mixtures[J]. The Canadian Journal of Chemical Engineering,1971,49(5):709-710.

[2]Chueh P L,Prausnitz J M. Vapor‐liquid equilibria at high pressures: Calculation of partial molar volumes in nonpolar liquid mixtures[J]. AIChE journal,1967,13(6): 1099-1107.

[3]Grieves R B,Thodos G.The critical temperatures of multicomponent hydrocarbon systems[J]. AIChE Journal,1962,8(4):550-553.

[4]Hicks C P,Young C L.Gas-liquid critical properties of binary mixtures[J].Chemical Reviews,1975,75(2): 119-175.

[5]Redlich O,Kister A T.Algebraic representation of thermodynamic properties and the classification of solutions[J]. Industrial & Engineering Chemistry,1948,40(2): 345-348.

[6]Prausnitz J M,Lichtenthaler R N,De Azevedo E G. Molecular thermodynamics of fluid-phase equilibria[M]. Pearson Education,1998.

[7]Teja A S,Garg K B,Smith R L.A method for the calculation of gas-liquid critical temperatures and pressures of multicomponent mixtures[J]. Industrial & Engineering Chemistry Process Design and Development,1983,22(4): 672-676.

[8]Wilson G M.Vapor-liquid equilibrium. XI. A new expression for the excess free energy of mixing[J].Journal of the American Chemical Society,1964,86(2): 127-130.

[9]Li L,Kiran E.Estimation of critical properties of binary mixtures using group contribution methods[J]. Chemical Engineering Communications,1990,94(1): 131-141.

[10]Donnelly H G,Katz D L. Phase equilibria in the carbon dioxide-methane system[J]. Industrial & Engineering Chemistry,1954,46(3): 511-517.

(本文文献格式：李红娟，苗鹏，倪福鑫.混合气体的临界温度计算[J].山东化工,2018,47(7):87-89.)