超声速绕钝板熵层不稳定性的研究

万兵

(天津大学 力学系, 天津 300072)

0 引 言

对于超声速飞行器的设计，层流-湍流转捩是必须要考虑的问题，也是流体力学研究的热点。在超声速飞行条件下，飞行器钝头体附近产生弓形激波。当气流穿过前缘附近激波角变化较大的弓形激波时，激波后的熵值变化较大，形成一层横向熵梯度较大的区域，称之为熵层。气体向下游流动，将包围着飞行器表面，从而增加表面气动热流[1]。因此研究熵层的流动稳定性，对于飞行器气动热防护的设计具有实际意义。

早期国外对钝体模型的实验研究发现，熵层对边界层稳定性的影响具有重要作用。Stetson[2]通过实验研究发现，在边界层外存在增长着的扰动，这表明熵层存在不稳定性。Lysenko[3]通过钝板实验也测量出熵层不稳定模态，同时指出这个不稳定模态影响着边界层内的第一模态。为了证实Stetson实验等关于熵层不稳定性的存在，Dietz & Hein[4]利用数值方法计算钝板模型，指出熵层有较小的增长率，其扰动演化与文中[4]Aerodynamisches Institute的实验结果吻合。Fedorov[5]根据Yakura[6]渐近法分析得到了熵层基本流方程表达式，在此基础上进行线性稳定性分析，得出同样的结果。

早在实验[3, 7-8]研究钝度对边界层转捩的影响时发现，在小钝度范围内增加钝度，转捩位置往下游移动；当钝度增加到一定大小时，转捩位置反而提前，这种现象称之为“transition reversal”。然而，Rosenboom & Hein[9]和Lei & Zhong[10]在计算N值时并没有发现这种现象，且钝度不断增加后，N值越小。Balacumar[11]和Kara et al[12]研究不同钝度的钝板、钝楔和钝锥的慢声波感受性时，得到的感受性系数亦是随着钝度的增加而始终减小。Fedorov[13]认为这种“transition reversal”的现象可能与熵层不稳定性有关。究竟是否存在“transition reversal”的现象是值得研究的。

本文将利用直接数值模拟计算马赫数为4.5、前缘为圆头的0°迎角钝板，并在此基础上进行线性稳定性分析，研究超声速绕钝板的熵层不稳定性。

1 控制方程和计算方法

1.1 控制方程

0°迎角超声速绕钝板流动是二维流动问题，直角坐标系(x,y)下二维可压缩流动N-S的无量纲守恒型方程为：

(1)

其中，U=[ρ,ρu,ρv,ρes]T,

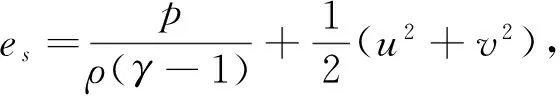
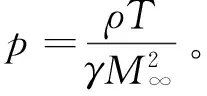
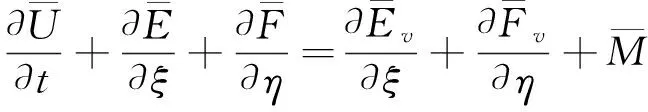
(2)

其中，

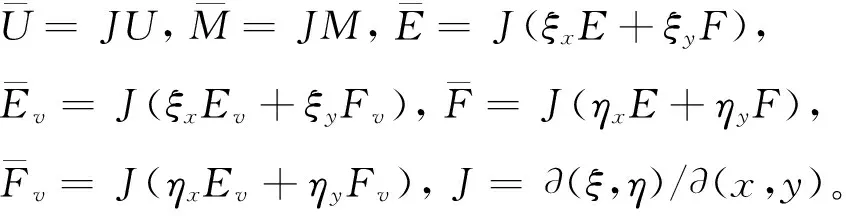
图1 坐标系和计算模型示意图Fig.1 Schematic diagram of coordinatesystem and computation model

1.2 计算参数和边界条件

本文选择马赫数为4.5、前缘为圆头的0°迎角钝板，可参考图1的示意图。气体为理想气体，黏度和热传导系数均采用Sutherland公式，流动条件见表1。

表1 超声速绕钝板流动条件Table 1 Conditions of supersonic flow over a blunt plate

对于直接数值模拟，计算模型可分为基本流计算和扰动演化。不同的计算模型边界条件也将不同。在对称面处，两个模型均采用对称边界条件；在出口处，各变量由上游三个点进行二次外推；在壁面处，基本流计算时采用无滑移绝热壁，扰动演化时速度脉动为0，温度脉动的法向导数为0；在远场，基本流计算时上边界等于来流值，扰动演化时上边界各变量的脉动值均为0。

1.3 数值方法

对于直接数值模拟，基本流计算模型切换到扰动演化计算模型时，为了避免切换过程中引入数值扰动，需要保证通量分裂方法和时间离散格式相同，以及边界层和熵层区域的空间离散格式相同。在这两个计算模型下，通量分裂方法均选择AUSM plus分裂方法，时间离散格式均选择三步Runge-Kutta格式。但对于空间离散，控制方程的对流项所选择的计算格式将不同。计算基本流时，对流项在激波附近采用五阶WENO格式(Jiang & Shu[14])，其他区域包括边界层和熵层区域采用五阶迎风格式；而进行扰动演化时，对流项统一采用五阶迎风格式。

本文的计算无量纲长度为1500，即7.5 m。在进行基本流计算时，计算域的流向网格和法向网格均为不均匀网格。对于法向网格分布，壁面附近网格较密，沿法向向上逐渐变稀，并且保证边界层区域内约包含101个法向点，熵层中广义拐点(广义拐点下文将介绍)附近的区域内约包含31个法向点。对于流向网格分布，头部区域较密，沿下游逐渐变稀。这样计算域的网格点数为1001×301。在进行扰动演化时，法向网格分布与上述一致，但流向网格为均匀分布，并保证一个扰动波波长大小的区域内至少包含21个流向点。这样计算域的网格点数为3001×301。数值计算程序由本课题组提供，其正确性可参见文献[15]。

2 计算结果

2.1 熵层和边界层

图2给出直接数值模拟得到的温度云图，同时给出激波、熵层外缘和边界层外缘的位置曲线，图2(a)给出的是流向区域为x=0～100的云图，图2(b)给出的是流向区域为x=100～1000的云图，其中区域为x=400～430的云图是红色矩形的放大图，粉色曲线表示激波位置，黄色曲线表示熵层外缘位置，黑色实线表示边界层外缘位置。边界层外缘与壁面之间为边界层区域，边界层外缘与熵层外缘之间为熵层区域。

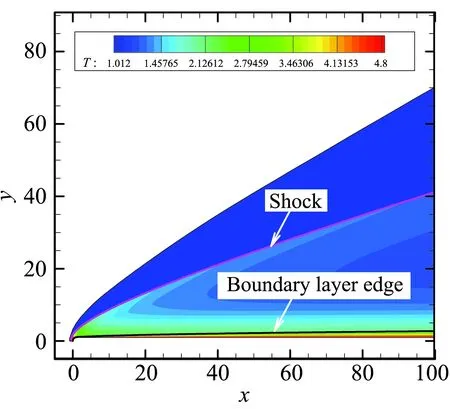
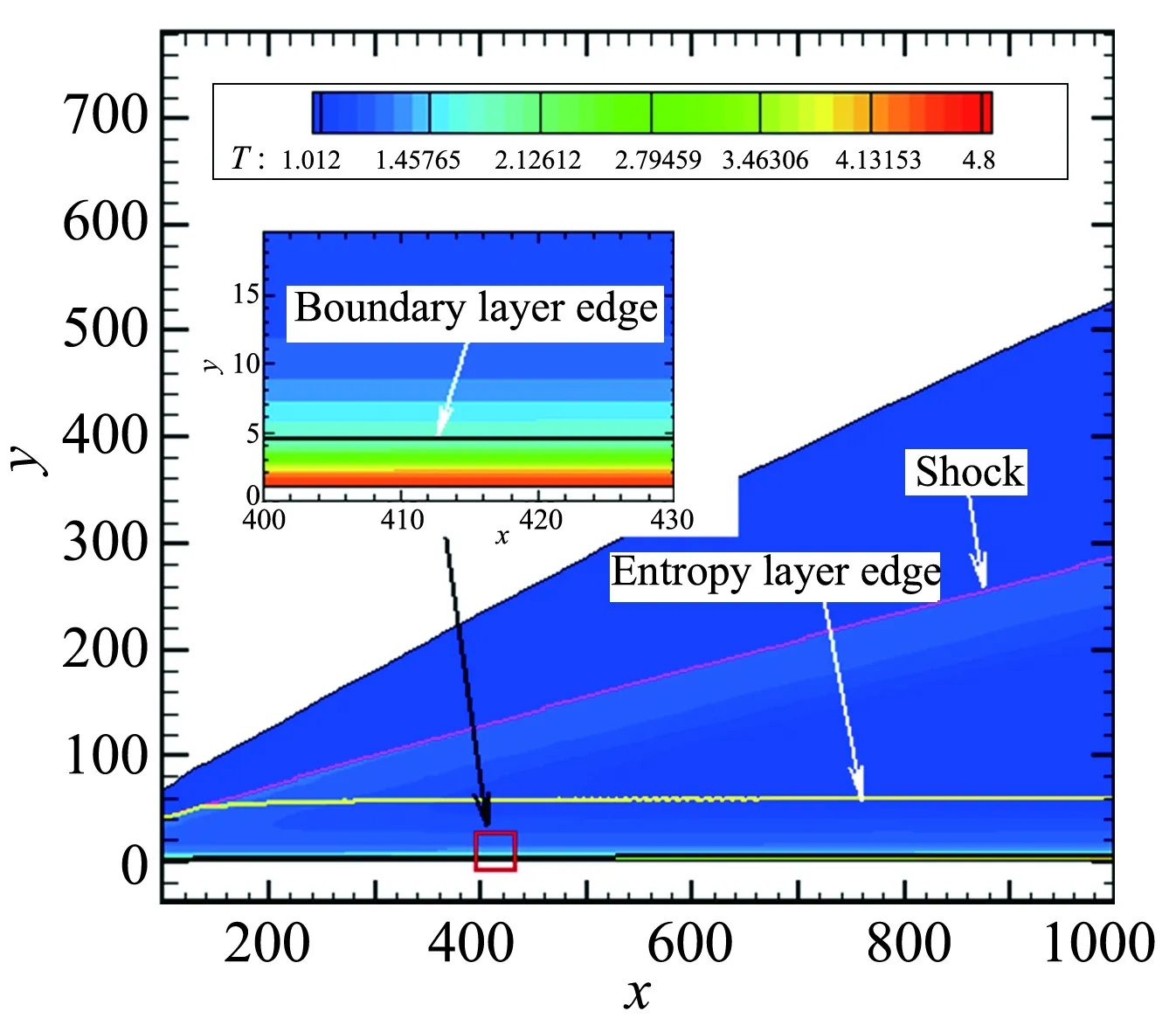
图2 温度云图Fig.2 Contour of temperature

边界层外缘位置可通过总焓h0参数确定。根据Kimmel & Klein[16]的经验，总焓由壁面开始过峰值后等于来流总焓的1.005倍，则为该流向位置的边界层外缘位置。例如，在x=200处，如图3(a)所示，给出总焓h0沿垂直壁面法向y的变化，黑点即为边界层外缘位置。对于熵层外缘的位置，可根据熵变的大小来确定，Laible[17]选择的经验方法是基于当地激波后熵变Δs的大小来判断，这样在确定每个位置的熵层外缘时需计算该位置激波后的熵变，增加了工作量。本文采用新的简单的经验方法，是基于某一固定值来确定。即，熵层外缘满足沿法向的熵变Δs等于驻点处熵变的0.01倍。某一位置的无量纲熵变Δs为：

图3(b)中给出熵变Δs沿垂直壁面法向y的变化，并根据上述方法确定出熵层外缘的位置。如此钝板流场中的熵层区域和边界层区域也就可以确定了，如图2所示。需要说明的是，在图2的x=0～1000流向范围内，没有明显看出熵层外缘与边界层外缘相交的趋势，换句话说，熵层外缘与边界层外缘夹角很小，熵层区域的特征仍然显著，熵层还没被“熵吞”。在这段区域内，熵层外缘与边界层外缘近乎平行，熵层流场在下游满足平行流假设。

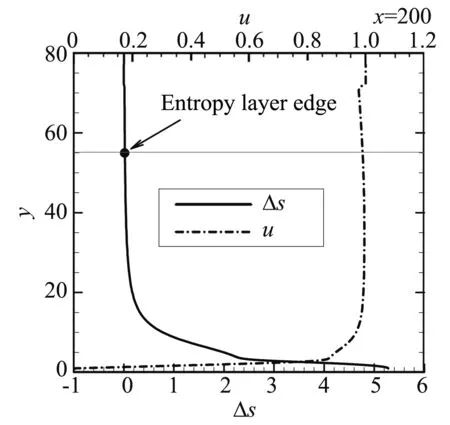
图3 总焓和熵变以及温度和速度沿垂直壁面法向的变化Fig.3 Total enthalpy, entropy, temperature and stream-wisevelocity along the wall-normal direction

2.2 熵层不稳定性

图4给出x=200的流向速度和ρ∂u/∂y曲线，可以看出ρ∂u/∂y曲线出现两个极大值，故存在两个广义拐点，分别位于边界层和熵层，其中熵层区域的广义拐点记为GIP-Entropy。根据无粘不稳定理论[18]，除了边界层中的不稳定模态，在基本流场中的熵层区域也有无粘不稳定模态。

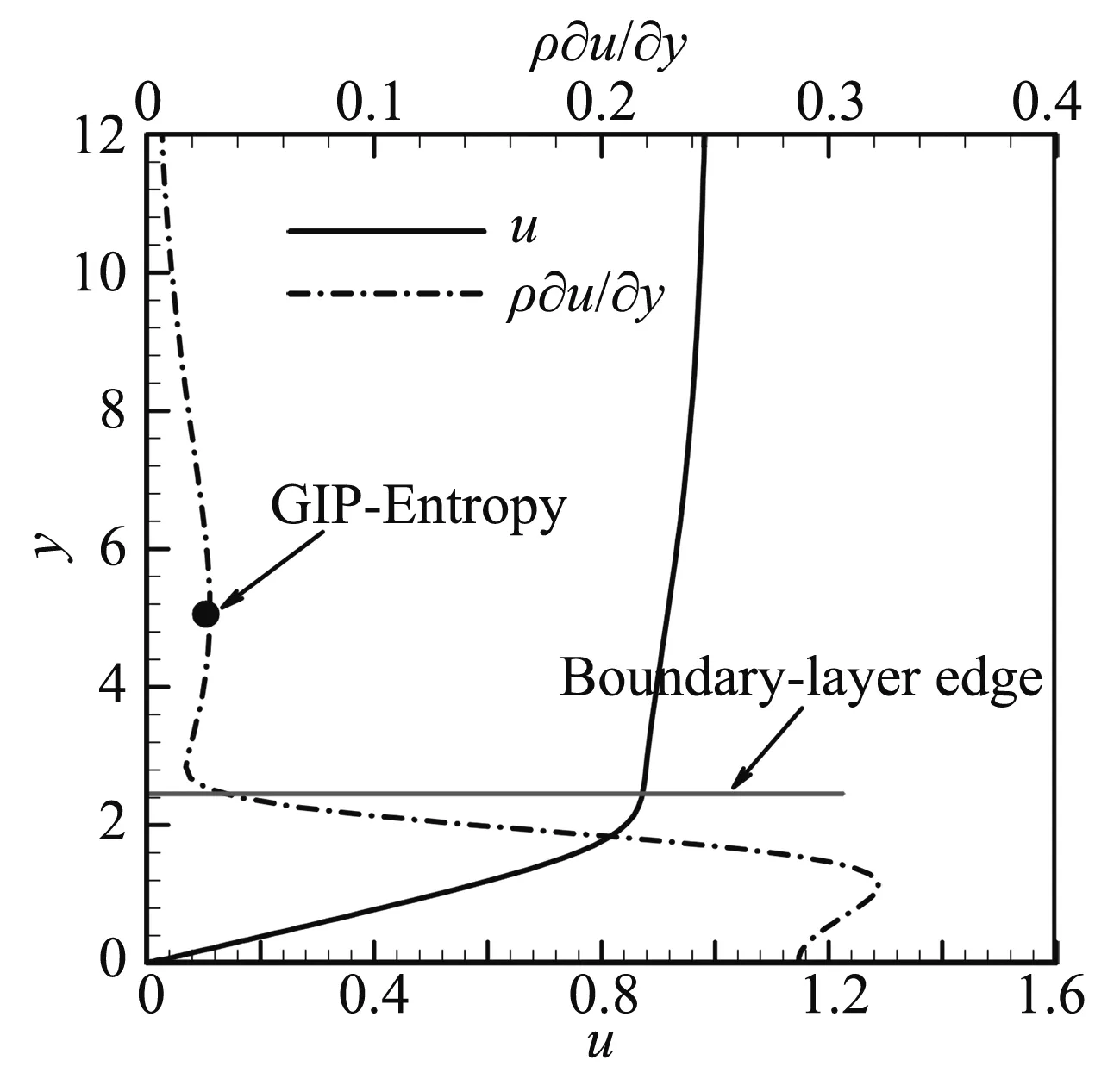
图4 流向速度和ρ∂u/∂y沿法向y的变化Fig.4 Stream-wise velocity and ρ∂u/∂yalong the wall-normal direction

为验证理论，针对熵层的广义拐点，进行线性稳定性理论(LST)分析。线性稳定性理论能够描述扰动的参数特征。它基于小扰动、平行流假设，忽略扰动方程的非线性项和基本量沿流向的变化，小扰动q′形式如下：

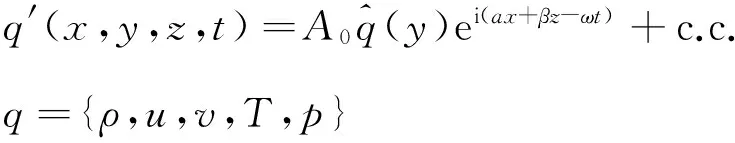
(3)

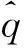
图5给出二维扰动的空间增长率-αi及相速度随圆频率的变化，可以看出中性解的上支界点的无量纲圆频率约为0.13，对应无量纲相速度约为0.92，与图4中广义拐点GIP-Entropy对应位置的流向速度相等，这表明该模态为熵层引起的不稳定模态。图6给出该不稳定模态的特征函数幅值分布，可以发现特征函数幅值的峰值对应的无量纲法向位置约为5.16，与图4中熵层中广义拐点的位置相等，进一步证明了熵层中存在不稳定模态。

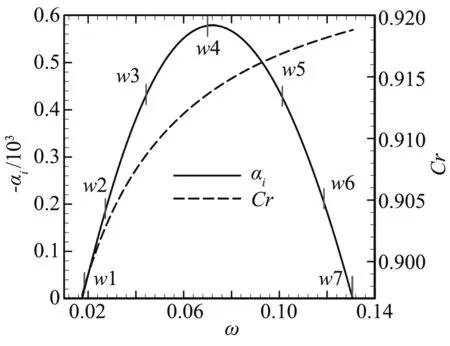
图5 空间增长率及相速度随圆频率的变化Fig.5 Spatial rate and phase velocity with circular frequency

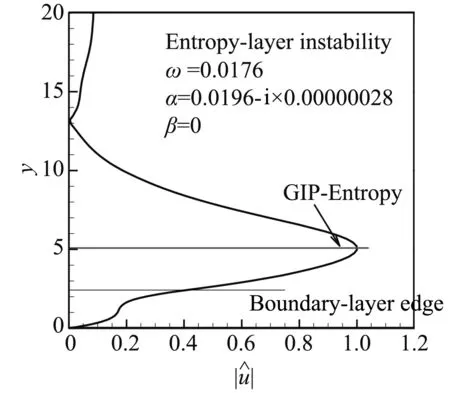
图6 流向速度特征函数幅值分布Fig.6 Amplitude distribution of stream-wisevelocity eigenfunction

图7给出x=200处不同圆频率下无量纲流向速度和温度的特征函数幅值分布，七个圆频率表示在图5中。图7 (a) 可以看出，较小圆频率时流向速度特征函数峰值在熵层广义拐点上，随着圆频率的增加，该峰值幅值逐渐减小，同时更靠近壁面的位置的幅值开始增加，并超过原峰值。可以发现，此时的峰值位置是图4中Boundary-layer edge和GIP-Entropy之间的极小值对应的位置。而图7(b)可以看出，不同频率下温度特征函数幅值的峰值位置均在熵层广义拐点GIP-Entropy上。

(a) 流向速度

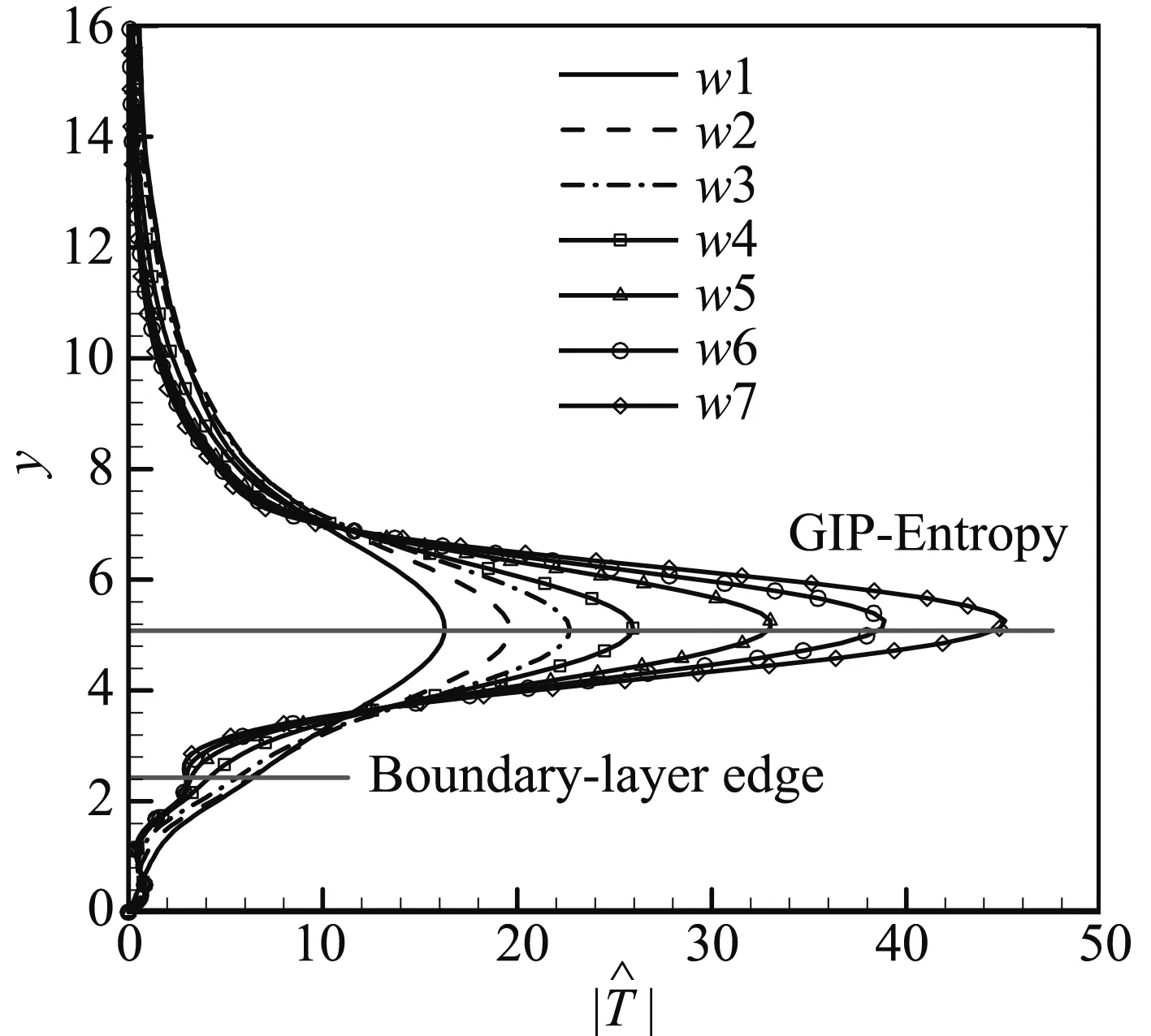
(b) 温度

图8和图9给出x=200的中性曲线及βr=0、 0.04、 0.08、 0.12时空间增长率随圆频率的变化，可以看出熵层存在着三维不稳定波，但二维不稳定波的空间增长率最大，因此在研究熵层扰动对边界层的影响时，选择熵层二维不稳定波。

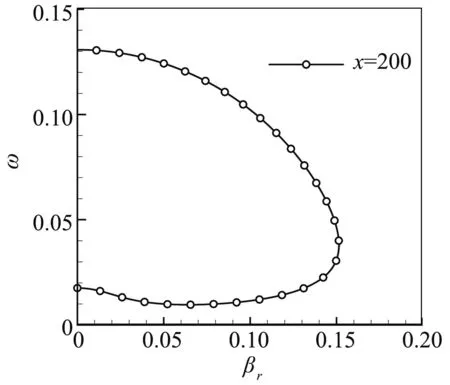
图8 中性曲线Fig.8 Neutral curve

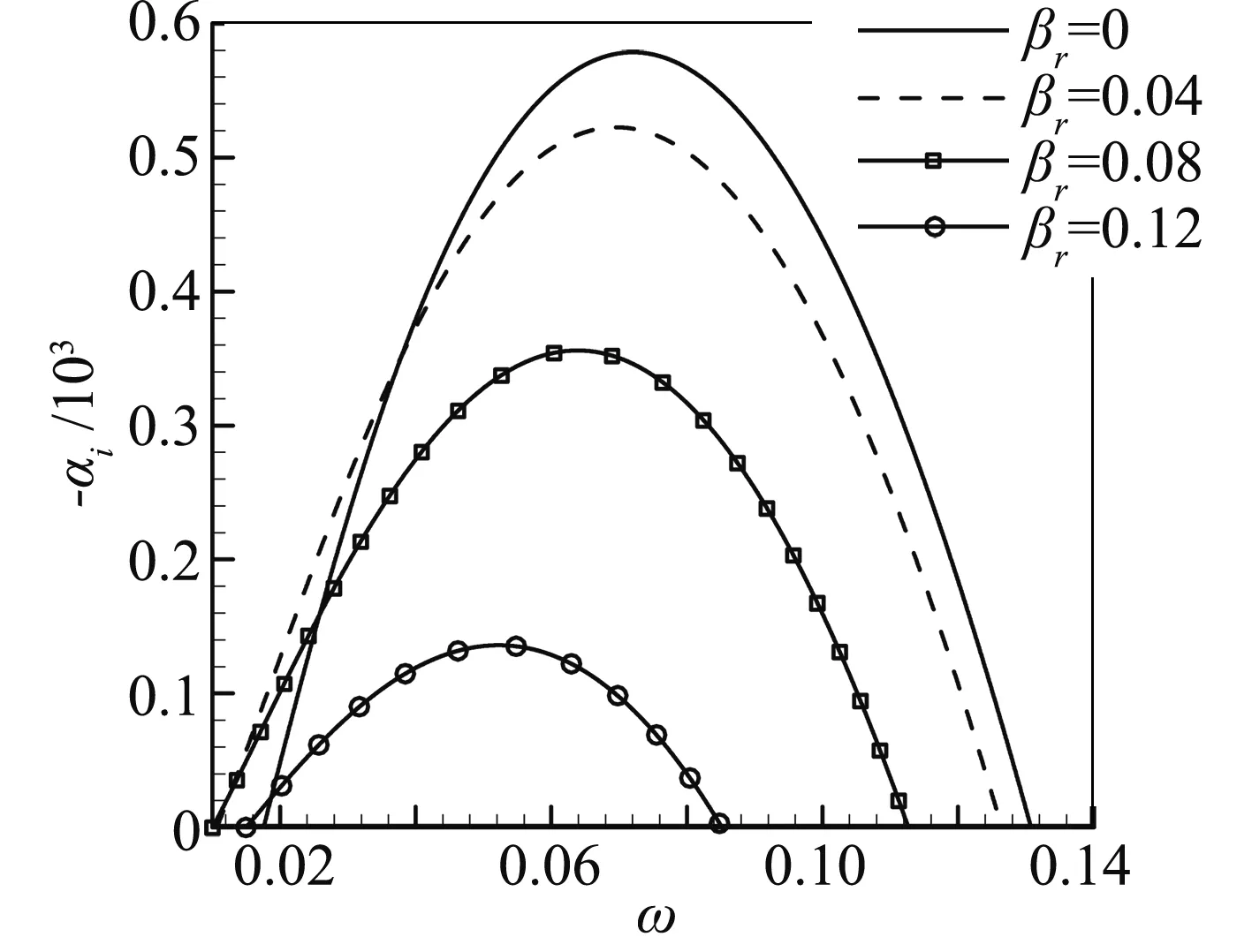
图9 不同展向波数下空间增长率随圆频率的变化Fig.9 Spatial rate along circular frequency withdifferent span-wise wave numbers

2.3 熵层扰动的演化

图10给出熵层二维中性曲线沿流向的变化，可以看出，中性曲线是半开放半封闭的。相比于边界层内中性曲线的左封闭右开放的形状，熵层的形状则相反，即左开放右封闭。换句话说，熵层扰动在上游是不稳定的，而到下游则是稳定的。图11给出无量纲圆频率为0.07的空间增长率沿流向的变化，可以看出空间增长率沿流向单调递减，且约在x=1000之后空间增长率为负，扰动开始衰减。另外注意到增长率为万分之一的数量级，扰动幅值变化很小。

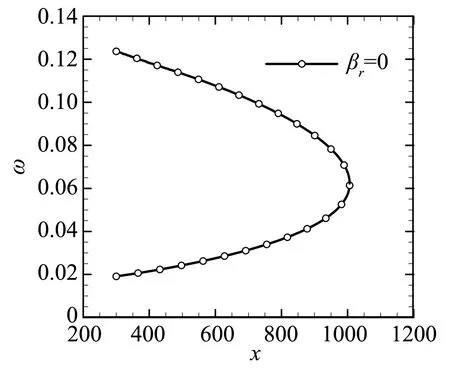
图10 熵层二维中性曲线沿流向的变化Fig.10 Two-dimensional neutral curve of entropy-layermode along stream-wise direction

图11 空间增长率沿流向的变化Fig.11 Spatial growth rate along stream-wise direction

为研究熵层扰动沿流向的演化过程，在x=400处加入通过稳定性分析得到的熵层扰动，进行扰动的数值模拟。图12给出密度脉动的云图，可以看出扰动主要分布于熵层区域，边界层内扰动未见到明显变化。

图13给出数值模拟的速度脉动的幅值曲线沿流向的变化，同时还给出线性PSE和LST的结果。可以发现约在x=1000之前，扰动幅值缓慢上升，在临界位置之后缓慢下降。而且线性PSE(线性PSE的程序验证参见文献[19])和LST的结果也与数值结果吻合得很好，由于LST对方程组作了平行流假设，说明了熵层内流动在下游具有很好的平行性。

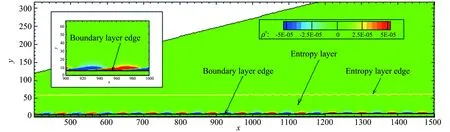
图12 密度脉动的云图Fig.12 Contour of density fluctuation

图13 速度脉动的幅值曲线沿流向的变化Fig.13 Amplitude of velocity fluctuation alongstream-wise direction

3 结 论

本文以前缘为圆头的0°迎角钝板为模型，通过直接数值模拟(DNS)计算基本流场，在此基础上利用线性稳定性(LST)分析研究了熵层中的不稳定性，同时根据经验方法确定了熵层区域和边界层区域，得到结论如下：

1) 熵层中存在广义拐点，通过稳定性分析表明熵层中存在不稳定扰动。另外，熵层存在三维不稳定波，但二维不稳定波增长率最大。

2) 扰动圆频率较小时流向速度特征函数峰值在熵层广义拐点上，随着圆频率的增加，该位置的峰值大小逐渐减小，同时边界层外缘与熵层广义拐点之间的某一位置的幅值开始增加，并超过原峰值大小。

3) 熵层不稳定模态集中在前缘附近，且空间增长率很小。利用直接数值方法模拟熵层扰动的演化过程，扰动在前缘附近幅值缓慢上升，之后缓慢下降。在距离前缘较远的范围内DNS结果与LST结果吻合得很好，表明熵层流场在下游具有很好的平行性。

需要指出的是，究竟是否存在“transition reversal”的现象还需要进一步研究。

致谢:本文所使用的DNS程序由赵磊博士提供，PSE程序由张存波博士提供，在这里特别感谢。

参考文献：

[1]Zhang Hanxin.The problem of entropy layer in the hypersonic flow[J].Acta Aeronautica et Astronautica Sinica, 1965, (2): 20-43.(in Chinese)张涵信.高超声速运动中的熵层问题[J].航空学报, 1965, (2): 20-43.

[2]Stetson K F, Thompson E R, Donaldson J C, et al.Laminar boundary layer stability experiments on a cone at Mach 8, Part 2: blunt cone[C]//22nd Aerospace Sciences Meeting, Reno, Nevada, USA: AIAA, 1984, 84-0006.

[3]Lysenko V I.Influence of the entropy layer on the stability of a supersonic shock layer and transition of the laminar boundary layer to turbulence[J].Journal of Applied Mechanics and Technical Physics, 1990, 31(6): 868-873.

[4]Dietz G, Hein S.Entropy-layer instabilities over a blunted flat plate in supersonic flow[J].Physics of Fluids, 1999, 11(1999): 7-9.

[5]Fedorov A, Tumin A.Evolution of disturbances in entropy layer on blunted plate in supersonic flow[J].AIAA Journal, 2004, 42(1): 89-94.

[6]Yakura J K.Theory of entropy layers and nose bluntness in hypersonic flow[J].Hypersonic Flow Research, 1962, 7(1): 421-470.

[7]Stetson K F, Rushton G H.Shock tunnel investigation of boundary-layer transition at M Equals 5.5[J].AIAA Journal, 1967, 5(5): 899-906.

[8]Softley E J, Graber B C, Zempel R E.Experimental observation of transition of the hypersonic boundary layer[J].AIAA Journal, 1969, 7(2): 257-263.

[9]Rosenboom I, Hein S, Dallmann U.Influence of nose bluntness on boundary-layer instabilities in hypersonic cone flows[C]//Proc.30th Fluid Dynamics Conference and Exhibit.Norfolk, VA, USA: AIAA, 1999, 99-3591.

[10]Lei J, Zhong X.Linear stability analysis of nose bluntness effects on hypersonic boundary layer transition[J].Journal of Spacecraft and Rockets, 2012, 49(1): 24-37.

[11]Balakumar P.Stability of supersonic boundary layers over blunt wedges[C]//Proc.36th Fluid Dynamics Conference and Exhibit.San Francisco, California, USA: AIAA, 2006, 06-3053.

[12]Kara K, Balakumar P, Kandil O.Effects of nose bluntness on stability of hypersonic boundary layers over a blunt cone[C]//Proc.37th Fluid Dynamics Conference and Exhibit.Miami, FL, USA: AIAA, 2007, 07-4492.

[13]Fedorov A V.Instability of the entropy layer on a blunt plate in supersonic gas flow[J].Journal of Applied Mechanics and Technical Physics, 1990, 31(5): 722-728.

[14]Jiang G S,Shu C W.Efficient implementation of weighted ENO schemes[J].Journal of Computational Physics, 1996, 126(1): 202-228.

[15]Zhao Lei.Study on instability of stationarycrossflow vortices in hypersonic swept blunt plate boundary layers[D].Tianjin: Tianjin University, 2016.(in Chinese)赵磊.高超声速后掠钝板边界层横流定常涡失稳的研究[D].天津: 天津大学, 2016.

[16]Kimmel R L, Klein M A, Schwoerke S N.Three-dimensional hypersonic laminar boundary-layer computations for transition

experiment design[J].Journal of Spacecraft & Rockets, 1993, 34(4): 409-415.

[17]Laible A C.Numerical investigation of boundary-layer transition for cones at Mach 3.5 and 6.0[D].Tucson, Arizona, USA: University of Arizona, 2011.

[18]Lees L, Lin C C.Investigation of the stability of the laminar boundary layer in a compressible fluid[M].Kitty Hawk, North Carolina, USA: NACA, 1946.

[19]Zhang Cunbo.Research on nonlinear mode interactions relating to supersonic boundary layer transition[D].Tianjin: Tianjin University, 2017.(in Chinese)张存波.与超声速边界层转捩有关的扰动非线性作用研究[D].天津: 天津大学, 2017.