股票市场仍然存在超额收益吗？——基于条件资本资产定价模型的研究

阳佳余 赵泽宇 张少东

资本资产定价模型(CAPM)是现代金融学的基石之一。这一框架讨论当投资者遵循均值方差原则选择最优资产组合时资产均衡价格是如何依风险而定。早期实证研究支持了这一观点，比如 Jensen 等(1972)以及 Fama和Macbeth(1973)的研究。随后出现了越来越多无法用 CAPM 模型解释的市场异象，比如市场规模效应(Banz，1981)、杠杆效应(Bhandari，1988)、账面市值比效应(Fama and French，1992)、流动性效应(Amihud，2002)、资产增长效应(Cooper et al.，2008)、现金流波动性(Haugen and Baker，1996)、异质性(Ang et al.，2006)以及投资效应(Titman et al.，2004)和动能效应(Jegadeesh and Titman，1993)等。

在传统 CAPM 模型中，一个重要假设是投资者具有相同投资期限，资产的β值不随时间变动。部分研究放松“所有投资者均只有一期投资期限”的假设，提出跨期资本资产定价模型(Intertemporal CAPM)。Merton(1973)认为，投资者不仅关心某一时期投资收益的最大化，还关心整个生存期间消费效用的最大化；投资风险不仅来源于证券价格的不确定性，还来源于消费品未来相对价格以及未来投资机会等，这些风险称为超市场风险，而实际中对各种额外风险进行准确的估价和补偿是困难的(Guo and Whitelaw，2006；Bali，2008；Bali and Engle，2010)。另一类研究则放松资产β值固定不变的假定，提出条件资本资产定价模型(Conditional CAPM)。条件 CAPM模型将时变性引入模型，使传统静态 CAPM 模型研究扩展到动态研究，并希望以此来解决诸如截面收益的拟合优度过低、定价误差过大、截面收益呈现规模效应和账面市值比效应等问题。宋军和吴冲锋(2008)对金融资产定价异常现象的研究进行了综述。

在实证研究方面，国内学者多遵循传统CAPM模型和FF三因子模型从时间序列角度进行分析，忽略了横截面分析。本文不仅研究了条件 CAPM 模型对收益数据的时序分析和截面分析，并对传统 CAPM 模型、FF三因子模型以及条件 CAPM 模型进行比较研究。

一、条件CAPM模型的分析框架

Bollerslev 等(1988)研究证明资产收益的条件协方差矩阵具有自回归效应。Jagannathan和Wang(1996)假设市场β,可变，将条件单因子模型转化为无条件双因子模型，表明条件 CAPM 模型能较好地解释股票横截面收益，而将人力资本纳入考虑后的无条件三因子模型在解释股票横截面收益上又有明显改进。Wu(2002)利用 GMM方法发现条件三因子模型能很好地解释美国股票市场的动量效应和反转效应。早在1973年，Fama Macbeth就对时变β,进行了研究，他们利用 60个月的滑动窗口技术(rolling window)计算出月度市场β,，并进行截面回归。一类模型假设β,是宏观经济变量和公司特征变量的函数，模型可以表示为：

其中，Zt-1是宏观变量的k维向量，δ0i是常系数，是k维宏观变量的系数。Shanken(1990)将市场β,表示成关于利率和利率波动率的线性模型，然后通过回归估计系数得到条件市场β,。Lettau和Ludvigson(2001)基于消费CAPM模型，利用作为预测变量对β,进行建模，其中表明消费、资产财富和收入共同的随机趋势。还有一类研究利用GARCH模型。不同于对市场β,直接建模，GARCH族模型考虑对条件方差和协方差建模。Bali(2008)利用二元GARCH模型估计条件市场β,，发现其能较好地解释 Fama-French的 25组资产组合平均收益。Engle(2002)提出了动态条件相关系数GARCH模型，通过估计股票组合和市场指数收益率的条件方差和动态相关系数得到时变β,系数。最后一种是非参数估计方法(Robinson，1989；Stanton，1997；Lewellen和Nagel，2006；Li和Yang，2009)。

传统模型的实证检验结果表明，在我国市场β对收益的横截面差异没有解释能力，阮涛和林少宫(2000)、陈浪南和屈文洲(2000)的研究均拒绝了SLB模型。对于FF三因子模型实证检验则没有得到统一的结论。范龙振和余世典(2002)发现，中国 A股市场存在明显的金融异象，市场β不能解释截面收益差异，但FF三因子模型的解释能力较好，类似观点的研究者还有朱宝宪和何治国(2002)以及 炘杨和陈展辉(2004)。基于多因子模型的研究，陈信元等(2001)讨论了财务杠杆和市盈率的作用。李家伟(2013)认为好β和坏β均不能解释股票回报的横截面信息。何孝星和于宏凯(2003)以条件 CAPM 作为风险调整模型分析证券投资基金业绩；罗登跃等(2007)基于条件CAPM 模型分析了深圳市场的时变β,效应。王宜峰等(2012)采用 GMM 方法分析了单状态变量条件CAPM模型和多状态变量条件CAPM模型。

本文的研究基于 Harrison和Kreps(1979)提出的随机折现因子(stochastic discount factor)模型和Lettau和Ludvigson(2001)研究。市场中无套利时，对于任意可交易资产存在一个随机折现因子，使得下式成立：。Et[⋅]表示基于 t时刻信息的条件期望因子，Ri,t+1为资产 i在 t+1时期的收益，Mt+1即为随机折现因子。，Re,t+1为有效集上任意一点的收益。称为条件线性因子模型。当其参数为恒定常数时转化为无条件线性因子模型：。

由条件线性因子模型可以推导出条件β,的表达式(Lettau & Ludvigson，2001)：。其中，R0,t是零β投资组合的收益，与随机折现因子不相关，βit为资产i的条件β，于是有：，。

如果条件矩是时变的，上式中的参数 bt一般而言不应是常数，不妨假设参数at、bt由 t时刻的具有预测作用的信息变量zt决定，特别的，可将参数at、bt写成如下线性形式：。将其带入可得：，于是有：。

在资本资产定价模型中，资产的收益可能与一些基础因子(fundamental factor)相关，将第j个基础因子记为fjt。例如FF三因子模型中，三个组合收益数据均为基础因子，并构成列向量 ft。定义，其中 ft+1为基础因子，化简为，其中。将其带入上式可写为：。其中，列向量，γ0是标量，是变量前的恒定系数。于是可得到β恒定的无条件多因子β表达式为：。其中，为零β组合收益的均值，且与随机折现因子无关。β可通过对收益数据的多因子回归分析得到，其表达式为：。由上式可得：。需要注意的是，此处得到的λ并不能直接解释为风险的价格。因为每一个无条件多因子模型都是从对应的条件多因子模型推导而来的。例如，假设条件 CAPM 模型可以写为表示市场收益，由此可以推导得到对应的无条件多因子模型为：。对于一个给定的条件线性因子模型，其中，条件β由下式给出：。其中，，是t时期基础因子的风险价格，表达式如下：。该式的风险价格与系数λ无直接关系，此方法不用于λ的估计，但得到的λ可用于计算，将这里的b'与通过定义得到的 bt进行比较。当没有进一步的假定条件时，不能计算出基础因子的风险价格，因为条件协方差未知。

二、传统CAPM模型和FF三因子模型的实证检验

(一)数据选择及其统计描述

本文研究对象为沪、深两市 A股市场，剔除 ST和金融行业以外的所有股票月度收益数据，样本期从1995年7月到2014年12月。数据来自于CCER数据库、锐思数据库和万德数据库。

在剔除 ST股票和金融行业股票后，采用 Fama和French(1992)的二维分组方法对符合要求的股票进行分组。分组原则如下：首先，在 t年 6月对股票依照市值(Size)和账面市值比(B/M)进行独立分组，以股票在t年6月末市值作为分组依据，账面市值比中的市值为 t-1年年末市值，对应的账面价值也为 t-1年所对应会计年度的账面价值。第二步，剔除在接下来 12个月中收益数据不完整的股票。第三步，把符合要求的股票按照市值和账面市值比各取5个分位数点，分为55组，其中Size-1到Size-5分别表示市值从最小到最大的组合，B/M-1到B/M-5分别表示账面市值比从最小到最大的组合。将每个组合内股票的月度收益数据按照市值进行加权平均，得到该组合的12个组合月度收益数据。重复这一操作，可得组合月收益的一组时间序列数据。将时序的组合收益数据进行简单平均后得到每个组合的平均月度收益数据如表1所示，收益数据来源于锐思数据库。

表1 组合平均月度收益

纵向地看，组合收益均值随着组合市值增大而减小；横向地看，除了(1，3)①(x，y)表示(Size-x，B/M-y)的组合。组合之外，组合的收益均值随组合的账面市值比增大而增大，即中国市场存在明显的规模效应和账面市值比效应。

(二)传统CAPM模型的测算

本文采用 Fama-MacBeth 的两步回归法②由于后文对条件 CAPM 进行回归检验时，采用的收益数据从1997年 7月开始，作为对照，对传统 CAPM的实证研究也选择从1997年7月开始进行。，首先，对每一组合的收益数据进行时间序列回归，得到在样本区间上恒定的组合β,值；然后用每个组合收益的时间均值对第一步获得的截面组合β,值进行回归，检验β,对截面收益的解释能力。其模型表达式为：

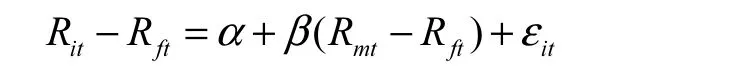
其中，Rit为组合 i的月度收益数据，计算方式如前文所述；Rmt为市场组合的收益，在实证中采用股票指数收益进行替代。由于本文研究对象包括沪、深两市股票，因此市场组合选用沪深300指数进行分析。沪深300指数从2005年4月8日起开始发布，反映了沪、深两市流动较性强且规模较大股票股价的综合变动情况。此前，上证综合指数和深证综合指数已于1991年7月15日和1991年4月3日起开始实时发布。

比较三个指数的时间趋势图可以发现③限于篇幅，未列出。，上证指数与沪深 300指数的走势大致吻合，且沪市总市值、发展程度和影响力均大于深圳证券交易市场，因此在 2005年 4月之前选择上证指数作为市场组合的模拟，2005年4月后选择沪深300指数作为市场组合的模拟。

Rft为无风险收益，本文采用锐思数据库中提供的无风险收益数据。具体而言，无风险收益数据的选择标准为：2002年8月前采用三个月定期银行存款利率；2002年8月到2006年10月采用三个月中央银行票据的票面利率；2006年10月后，采用上海银行间3个月同业拆放利率。

首先，对组合收益数据进行时序回归得到每个组合在样本区间的组合β，结果如表2所示。传统 CAPM 模型的市场β,值均显著异于零，说明市场组合的收益可以捕捉到组合时序的收益变化；而且除了 Size-2的五个组合外，大都表现出随着账面市值比增加而增大的趋势，在市场超额收益大于零的情况下，可以部分解释账面市值比效应；纵向的看，市场β,并未表现出明显的趋势性，规模效应不能得到解释。此外，如果静态CAPM 模型成立，则回归得到截距项系数α应为零。表2中，截距项系数α基本表现出随着规模增大而减小的规模效应特征，随着账面市值比增大而增大的账面市值比效应特征。市值较小的组合中，截距项系数α几乎全部显著异于零；账面市值比较大的组合中，α显著的组合也多于不显著的组合。其次，用组合收益的时间均值对第一步得到的组合截面β数据进行回归：。

表2 传统CAPM模型的时间序列回归

从表3可以看到方程的拟合优度仅有2.64%,，说明传统CAPM模型对截面收益的解释能力较弱，组合截面收益的大部分并不能被静态市场β,值所捕捉。同时，市场β,的系数为1.87，并不显著，这与Fama和French(1992)的研究结果相同，恒定的组合β,不能解释截面收益的情况。

表3 传统CAPM模型的截面分析

(三)FF三因子模型的经验分析

由于市场存在较强的规模效应和账面市值比效应，Fama和French(1992)提出了三因子模型，三个因子分别为市场组合的超额收益、用于捕捉规模效应的因子(SMB)和用于捕捉账面市值比效应的因子(HML)。SMB和HML的构造方法均基于FF的二维分组方式，将每一时期的股票规模分为 S、B两组，账面市值比分为 L、M、H三组。每一期得到的 6组数据(S/L、S/M、S/H、B/L、B/M、B/H)中，用小市值股票的收益数据减去大市值股票收益数据，得到 SMB；用账面市值比大的股票收益数据减去账面市值比小的股票收益数据，得到HML。即SMB=(S/L+S/M+S/H)-(B/L+B/M+B/ H)；

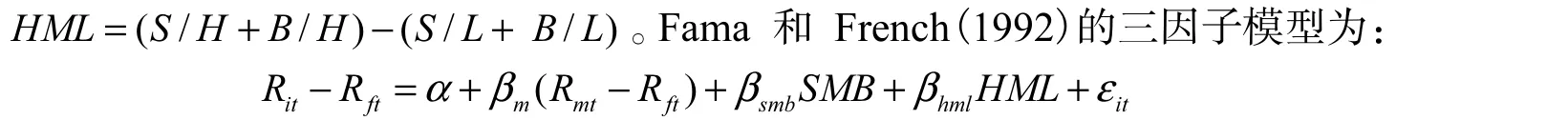
其中，βm表示市场β，βsmb表示规模效应因子对应的β，βhml表示账面市值比效应对应的β，上式中其他各符号代表的意义同前。

第一步，对组合的收益数据进行时序回归。从表4可以看出，市场β均是显著的，说明市场组合收益是解释组合收益的时间序列变化不可或缺的变量，且其拟合值与 t值均未有明显下降。规模因子β的 t值随着规模的增大而减小，且除了规模最大的几个组合外，均显著异于零，说明随着规模的增大，规模效应因子对时间序列的收益变化捕捉能力减弱。账面市值比因子β的 t值大体上呈现出随着账面市值比增大而增大的趋势，当账面市值比较大或较小时，账面市值比因子是解释时序收益数据的必要因子，当账面市值比落于中间组合时，该因子对时序收益的解释能力大大降低。

B/M-1 B/M-2 B/M-3 B/M-4 B/M-5 B/M-1 B/M-2 B/M-3 B/M-4 B/M-5

表4 FF三因子模型的时间序列分析

将表4与表2进行对比，发现三因子模型得到的组合α更接近于零，且不再表现出随规模和账面市值比变化的趋势，此外，仅有少数组合的α显著。这些均表明，从时间序列数据上来看，三因子模型是比传统静态 CAPM 更优的模型。静态 CAPM 模型对收益数据进行时间序列回归时，拟合优度从 54.39%,到90.58%,不等；FF三因子模型的拟合优度则普遍高于90%,，表现出明显优势。

第二步，用组合收益时间均值对得到的组合的βm、βsmb、βhml截面数据进行回归：

由表5可知，三因子模型可以很好地提高对截面收益的解释能力，模型的拟合优度从静态 CAPM 的 2.64%,大幅提升到 83.15%,。三个β值系数中，规模效应估计系数s和市值效应估计系数h均非常显著，但市场组合β的系数并不显著。

三、条件CAPM模型的经验研究

(一)获得时序α值以及β,值

条件CAPM模型中，β,是随时间可变的，本文采用Fama-MacBeth(1973)滑动窗口的方法获得时序β,值。作为一种非参方法，滑动窗口模型不会因模型参数设定不当而导致可能错误。根据滑动窗口方法，当期β值用滞后 24个月的月度收益数据获取，即t期的组合β值由t-24到t-1期的组合月度收益回归得到。每个组合得到的时序组合β值是从1997年7月到2014年12月共有210个值的β的时间序列。表6列出了静态CAPM模型下各组合α、β值和各组合时序α、β值的统计特征。

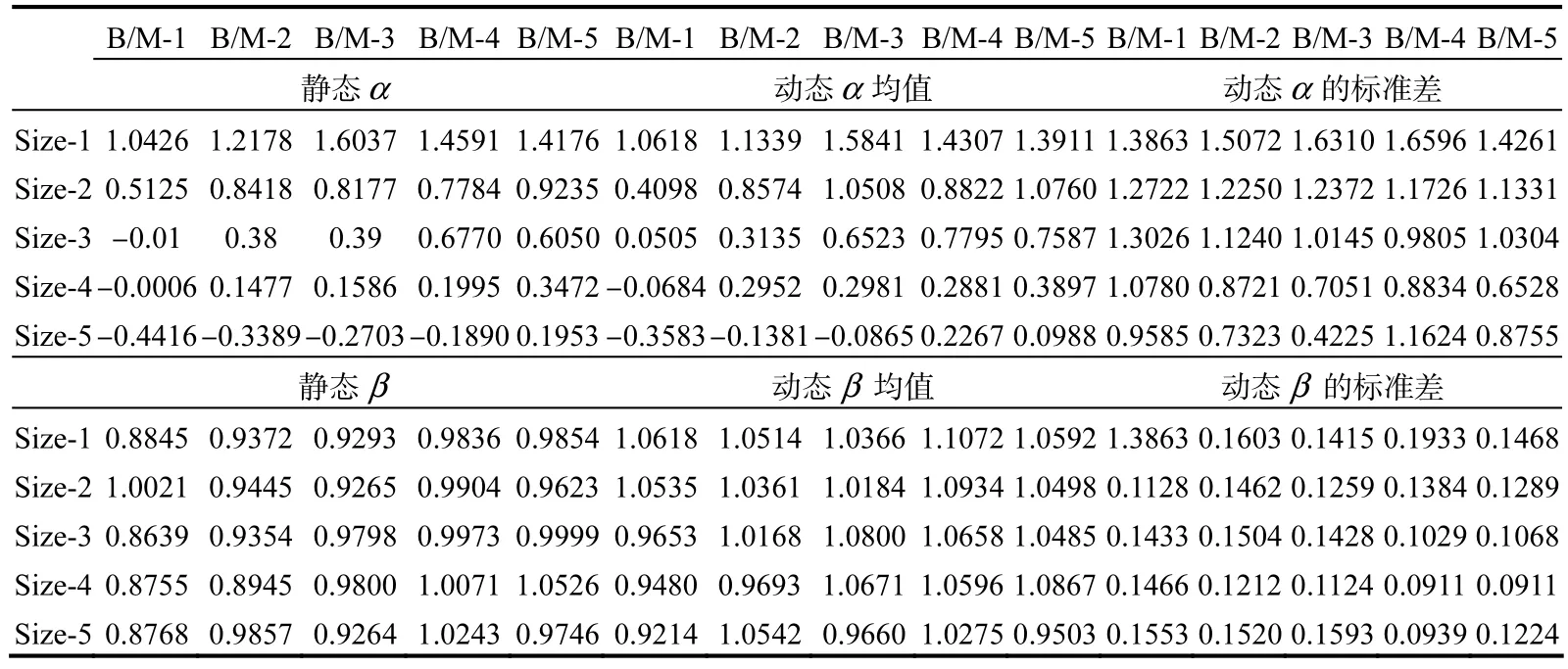
表6 静态β和动态β的统计特征

验证条件 CAPM 是否成立即为验证条件α是否为零(Lewellen & Nagel，2006)，越接近零，则模型越优。总体上条件 CAPM 并没有有效降低定价误差，只有当规模较小或较大时，条件α略小于静态CAPM的无条件α，表现出一定优势。

静态β和动态β的均值有显著差异。本文仅选取两个极端组合(1，1)和(5，5)，绘制出了组合静态β和组合动态β的分布情况。由图中可以看出，组合β随时间动态波动，放松恒定β这一假设条件可以更好地模拟实际市场情况。

图1 组合(1，1)动态β的波动情况

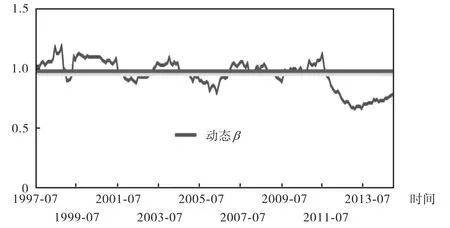
图2 组合(5，5)动态β的波动情况

(二)确定状态变量

国外文献中常用的状态变量有滞后的市场收益、国债利率、股息收益率还有期限利差、消费财富比(cay)、D/P等。国内学者王宜峰(2012)选择了 Shibor、广义货币余额(M2)变动率、社会消费品零售总额变动率、固定资产投资变动率、CPI作为状态变量进行实证研究。本文选择状态变量的原则有：首先要尽可能涵盖影响β和收益的宏观或金融因素，主要包括市场因素、货币因素、国际贸易因素、投资因素、价格因素、汇率因素等；其次，所选择状态变量要能反映β的时变特性。

基于此，本文首先选择如下变量作为备选状态变量。货币因素包括 M0同比增长率、M1同比增长率、M2同比增长率；汇率因素包括美元兑人民币汇率；国际贸易因素包括月度贸易差额、月度贸易差额同比增长率；价格因素包括消费者价格(CPI)同比增长率、商品零售价格指数(RPI)同比增长率、生产价格指数(PPI)同比增长率；投资因素包括固定资产投资完成额；消费因素包括社会零售品消费总额同比增长率；市场因素包括滞后 1、2、3期的市场收益率；其他综合因素包括宏观经济预警指数①预警指数是把经济运行的状态分为 5个级别，“红灯”表示经济过热，“黄灯”表示经济偏热，“绿灯”表示经济运行正常，“浅蓝灯”表示经济偏冷，“蓝灯”表示经济过冷。、宏观经济一致指数②一致指数是反映当前经济的基本走势，由工业生产、就业、社会需求(投资、消费、外贸)、社会收入(国家税收、企业利润、居民收入)4个方面合成。、宏观经济先行指数③先行指数是由一组领先于一致指数的先行指标合成，用于对经济未来的走势进行预测。、宏观经济滞后指数④滞后指数是由落后于一致指数的滞后指标合成得到，它主要用于对经济循环的峰与谷的一种确认。、消费者信心指数⑤消费者信心指数(Consumer Confidence Index，CCI)是反映消费者信心强弱的指标，是综合反映并量化消费者对当前经济形势评价和对经济前景、收入水平、收入预期以及消费心理状态的主观感受，是预测经济走势和消费趋向的一个先行指标，是监测经济周期变化不可缺少的依据。、消费者满意指数、消费者预期指数⑥消费者预期指数是普通消费者对收入、生活质量、宏观经济、消费支出、就业状况、购买耐用消费品和储蓄在未来一年的预期及未来两年在购买住房及装修、购买汽车和未来6个月股市变化的预期。。前几个变量模拟的都是单一的宏观或经济因素，最后几个指数指标在编制时就考虑了多种宏观和金融指标，是一种综合指数从而反映了多种因素变化情况。第一步，研究各组合时变β与状态变量的相关系数，相关性越强说明备选变量与时变β的波动特征更相似，能够在一定程度上模拟时变β的变动⑦由于篇幅所限，完整的相关系数表不在此处列示，如有需要可向作者索要。。第二步，用各个备选状态变量对每个组合的时序β进行回归，看哪些变量能较好捕捉β变化，衡量标准为各备选状态变量对时变β回归的拟合优度值。

由表7可知，当用单一备选状态变量对组合收益进行时序回归时，依拟合优度大小排序，前几名的备选状态变量与之前通过计算相关系数得到的状态变量呈现了高度的重合性。本文采用 CPI同比增长率、RPI同比增长率、PPI同比增长率、社会消费品零售总额同比增长率、美元兑人民币汇率、无风险利率、固定资产完成额、宏观经济预警指数、宏观经济一致指数、宏观经济滞后指数这些变量对时变β进行模拟。

表7 备选状态变量的拟合优度

(三)条件CAPM对时序收益和截面收益的解释

条件CAPM模型的一般表达式如下：

参考Lettau和Ludvigson(2005)、Santos和Veronesi(2006)的模型，将静态CAPM模型中恒定的α和β改写成单一状态变量线性函数。组合收益不仅受到市场组合影响，还受到状态变量以及状态变量与市场组合收益交叉项影响，如下式所示：

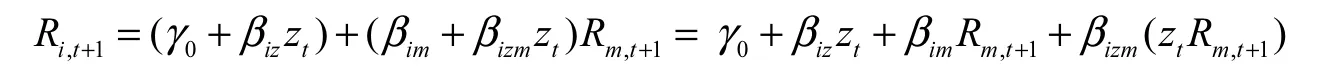
对每个投资组合分别做 24个状态变量的单变量时间序列分析，得到各状态变量对应的β值、市场组合β值、交叉项对应的β值以及回归截距项、拟合优度等信息，如表8所示。

表8 考虑单一状态变量的条件CAPM模型时序回归结果(仅列出部分组合结果)

续表8

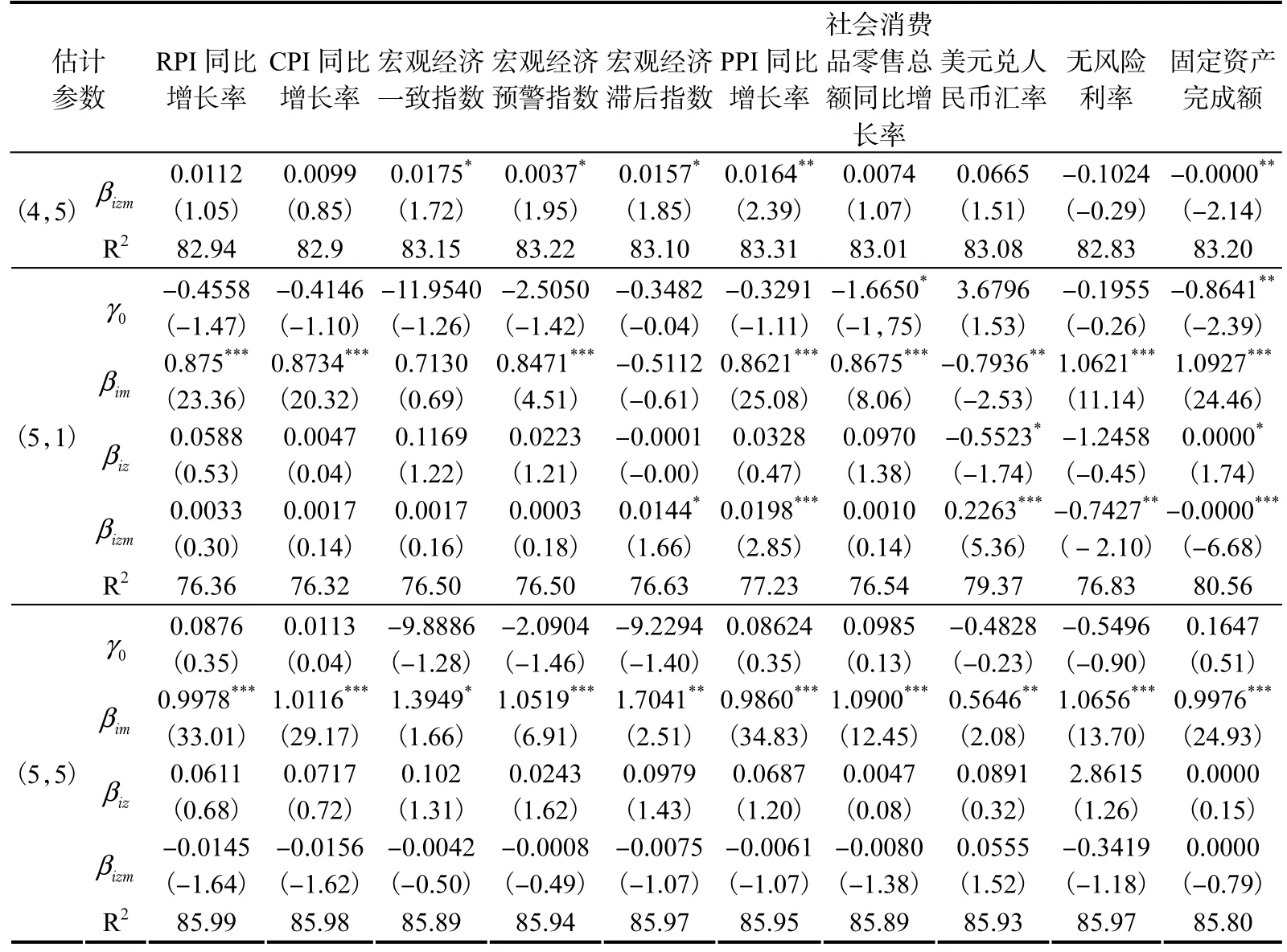
续表8

结合表2、表4和表8可知，当状态变量衡量的是价格因素和投资因素时，各组合条件α与静态 CAPM 无条件α非常接近，小规模组合的条件α均显著异于零。当RPI、CPI、PPI同比增长率进入模型后，条件α表现出较明显的规模效应特征和账面市值比效应特征，即条件α随着规模的增大而减小，随着账面市值比的增大而增大；当固定资产完成额进入模型后，条件α表现出较为明显的账面市值比效应特征而未表现出规模效应特征。因此，价格因素和投资因素作为状态变量时，从时间序列角度的定价误差来看，条件CAPM并不优于静态CAPM。

当状态变量为其他变量时，从时序定价误差的角度看，条件 CAPM 不仅优于静态CAPM模型，也比FF三因子模型表现出更好定价能力。当状态变量为无风险利率时，表现出轻微规模效应特征，但所有投资组合的条件α均不显著。当状态变量为汇率因素时，仅有个别条件α显著，比如组合(3，1)和(4，1)。当考虑社会零售品消费总额同比增长率时，仅有组合(5，1)与(5，4)在 10%,显著性水平上显著。当其他综合指数作为状态变量时，条件α不仅没有表现出明显规模效应特征和账面市值比效应，且条件α均不显著，时序角度定价能力较强①表8中状态变量为“固定资产完成额”时，所有投资组合的估计系数值过小，不进入下一步截面回归。。从时序回归的拟合优度来看，各个状态变量对特定组合的拟合优度差异不大。条件 CAPM 的时间序列拟合优度大体上与静态 CAPM相当，与FF三因子模型的拟合优度相差较大。

下面进行截面回归分析，用各组合收益的时间均值对上面得到的三个β值进行OLS回归，研究加入状态变量后，对截面收益的解释能力是否有所提高。

由表9可知，通过状态变量来模拟时变β可以增强对截面收益的解释力，拟合优度均有不同程度提高。

表9 条件CAPM模型的截面回归结果

当状态变量为宏观预警指数、PPI同比增长率和美元兑人民币汇率时，市场组合β的系数显著异于 0，说明这三个状态变量的加入可以提高市场β对截面收益的解释能力；当状态变量为宏观预警指数和美元兑人民币汇率时，交叉项β的系数显著，交叉项β也对截面系数具有一定的解释能力。如前所述，静态 CAPM 模型和FF三因子模型的截面回归中，市场β的系数均不显著，但在条件CAPM中，当状态变量为宏观经济预警指数、PPI同步增长率、美元兑人民币汇率时，市场β的系数显著。尤其是当状态变量为宏观经济预警指数时，模型拟合优度最高，同时三个β值系数均显著异于 0。从截面上看，可认为宏观经济预警指数是最优的状态变量。此外，PPI同比增长率作为状态变量时也获得了较高的 R2提升，且状态变量β值及市场组合β值的系数均显著异于0。因此，价格因素与利率因素的状态变量，和一些综合指数如宏观经济预警指数、一致指数等，都可以作为较好的状态变量选择，从而在截面上更好地改进静态CAPM。

四、结 论

本文放松了传统 CAPM 模型的恒定参数假定，在随机折现因子的框架下，运用Fama-MacBeth的两步骤回归方法，从条件CAPM模型的角度出发，研究引入时变β对资本资产定价模型能否有所改进。首先从时间序列角度进行分析，获得每个投资组合对应不同状态变量时相应的β值，并分析不同因子对时序收益的解释能力；第二步用截面的组合收益时间均值对第一步获得β值进行 OLS回归，观察加入时变特性后的模型是否提高了截面回归的拟合优度。对于状态变量的选择采用的是通过滑动窗口方法估计的组合β值时间序列，在已知时序β值的条件下，依据相关系数和变量对β波动捕捉情况来选择状态变量。总体上，本文即是通过传统CAPM模型、FF三因子模型以及条件CAPM模型的横向比较，判断条件CAPM模型在中国股票市场的适用性。

通过对依据规模和账面市值比分组的25个投资组合进行传统CAPM模型的经验分析，我国 A股市场存在明显的规模效应和账面市值比效应；市场组合对时序收益的解释能力受组合影响较大，不同组合的静态α值也反映较大定价误差；恒定市场β对组合的截面收益几乎没有解释力。FF三因子模型不仅能够稳定地解释组合时序收益，且拟合优度均达到 90%,以上，定价误差也有效降低；在截面上，三因子模型也获得了很高拟合优度值，但在截面分析中市场组合β的系数依旧不显著，并没有改变传统CAPM模型中市场组合β对截面收益解释乏力的事实。

通过滑动窗口回归得到各个组合的时序α、β值，进一步证实了组合β的时变特性，说明简单假定β恒定的做法并不可取。比较相关性及不同宏观、金融变量对时序β的拟合情况，发现价格因素、汇率因素、利率因素、投资因素、产出因素和综合指数均可以在一定程度上模拟β的时变特征。从时序回归角度看，条件CAPM模型对时序收益的拟合能力相比于传统CAPM模型并没有显著提升，价格因素和投资因素也没有有效改善定价误差；但当状态变量为汇率因素、利率因素、产出因素或综合指数时，此时定价误差不仅明显小于传统 CAPM 模型，也优于 FF三因子模型。从截面回归角度看，相比于传统 CAPM 模型，时变β的引入可以明显提升模型对截面收益的解释力，但不同状态变量对模型拟合优度的提升程度有较大差异，而且状态变量的引入可以在很大程度上提升市场β在模型中的解释能力，这是对传统CAPM模型和FF三因子模型非常直观的改善。

［1］陈浪南，屈文洲.资本资产定价模型的实证研究[J].经济研究，2000(4)：26-34.

［2］陈信元，张田余，陈冬华.预期股票收益的横截面多因素分析：来自中国证券市场的经验证据[J].金融研究，2001，6(22)：22-35.

［3］范龙振，余世典.中国股票市场的三因子模型[J].系统工程学报，2002，17(6)：537-546.

［4］何孝星，于宏凯.条件 CAPM 下我国证券投资基金业绩的实证研究[J].南开经济研究，2003(6)：68-71.

［5］李家伟.极端事件真的能塑造投资者预期？——基于“坏β”“好β”资产定价理论的实证检验[J].经济学(季刊)，2013，13(1)：151-174.

［6］罗登跃，王春峰，房振明.深圳时变 Beta条件 CAPM 实证研究[J].管理工程学报，2007(4)：102-109.

［7］阮 涛，林少宫.CAPM 模型对上海股票市场的检验[J].数理统计与管理，2000，19(4)：12-17.

［8］宋 军，吴冲锋.金融资产定价异常现象研究综述及其对新资产定价理论的启示[J].经济学(季刊)，2008，7(2)：701-730.

［9］王宜峰，王燕鸣，张颜江.条件 CAPM 与横截面定价检验：基于中国股市的经验分析[J].管理工程学报，2012，26(4)：137-145.

［10］杨 炘，陈展辉.中国股市三因子资产定价模型实证研究[J].数量经济技术经济研究，2004(12)：137-141.

［11］朱宝宪，何治国.β值和帐面/市值比与股票收益关系的实证研究[J].金融研究，2002(4)：71-79.

［12］Amihud Y.Illiquidity and Stock Returns：Cross-section and Time-series Effects[J].Journal of Financial Markets，2002(5)：31-56.

［13］Ang A.，Robert J.H.，Xing Y.H.，Zhang X.Y.The Cross-section of Volatility and Expected Returns[J].Journal of Finance，2006(61)：259-99.

［14］Bali T.G.，Engle R.F.The Intertemporal Capital Asset Pricing Model with Dynamic Conditional Correlations[J].Journal of Monetary Economics，2010，57(4)：377-90.

［15］Bali T.G.The Intertemporal Relation Between Expected Returns and Risk[J].Journal of Financial Economics，2008，87(1)：101-31.

［16］Banz R.W.The Relationship Between Return and Market Value of Common Stocks[J].Journal of Financial Economics，1981，9(1)：3-18.

［17］Bhandari L.C.Debt/Equity Ratio and Expected Common Stock Returns：Empirical Evidence [J].The Journal of Finance，1988，43(2)：507-28.

［18］Bollerslev T.，Engle R.F.，Wooldridge J.M.A Capital Asset Pricing Model with Time-varying Covariances[J].The Journal of Political Economy，1988，96(1)：116-31.

［19］Cooper M.J.，Gulen H.，Schill M.J.Asset Growth and the Cross Section of Stock Returns [J].Journal of Finance，2008，63(4)：1609-52.

［20］Engle R.Dynamic Conditional Correlation：A Simple Class of Multivariate Generalized Autoregressive Conditional Heteroskedasticity Models[J].Journal of Business & Economic Statistics，2002，20(3)：339-50.

［21］Fama E.F.，French K.R.The Cross-section of Expected Stock Returns[J].Journal of Finance，1992，47(2)：427-65.

［22］Fama E.F.，MacBeth J.D.Risk，Return，and Equilibrium：Empirical Tests[J].The Journal of Political Economy，1973：607-36.

［23］Guo H.，Whitelaw R.F.Uncovering the Risk-return Relation in the Stock Market[J].The Journal of Finance，2006，61(3)：1433-63.

［24］Haugen Robert A.，Nardin L.Baker.Commonality in the Determinants of Expected Stock Returns[J].Journal of Financial Economics，1996，41(3)：401-39.

［25］Jagannathan R.，Wang Z.The Conditional CAPM and the Cross-section of Expected Returns[J].The Journal of Finance，1996，51(1)：3-53.

［26］Jegadeesh N.，Titman S.Returns to Buying Winners and Selling Losers：Implications for Stock Market Efficiency[J].Journal of Finance，1993，48(1)：65-91.

［27］Jensen M.C.，Black F.，Scholes M.S.The Capital Asset Pricing Model：Some Empirical Tests[J].Social Science Electronic Publishing，1972，94(8)：4229-32.

［28］Lettau M.，Ludvigson S.Resurrecting the(C)CAPM：A Cross-sectional Test When Risk Premia Are Time-varying[J].Journal of Political Economy，2001，109(6)：1238-87.

［29］Lewellen J.，Nagel S.The Conditional CAPM Does Not Explain Asset-pricing Anomalies[J].Journal of Financial Economics，2006，82(2)：289-314.

［30］Li Y.，Yang L.Underconditioning and Overconditioning：Testing the Conditional CAPM and the Conditional Fama-French Three-factor Model[R].Working Paper，Cornell University，Ithaca，NY，2009.

［31］Merton R.C.An Intertemporal Capital Asset Pricing Model[J].Econometrica，1973，41(5)：867-87.

［32］Robinson P.M.Nonparametric Estimation of Time-varying Parameters[M].Verlag Berlin Heidelberg：Springer，1989.

［33］Shanken J.Intertemporal Asset Pricing：An Empirical Investigation[J].Journal of Econometrics，1990，45(1)：99-120.

［34］Stanton R.A Nonparametric Model of Term Structure Dynamics and the Market Price of Interest Rate Risk[J].The Journal of Finance，1997，52(5)：1973-2002.

［35］Titman S.，Wei K.，John C.，Xie F.X.Capital Investments and Stock Returns[J].Journal of Financial and Quantitative Analysis，2004，39(4)：677-700.

［36］Wu X.A Conditional Multifactor Analysis of Return Momentum[J].Journal of Banking &Finance，2002，26(8)：1675-96.