基于3-RPS 并联机构的视觉设备安装 平台建模与仿真

王祥，王杰，高磊

（西安工程大学 机电工程学院，陕西 西安 710048）

0 引言

机器人视觉在纺织、检测以及工业等领域得到了广泛的应用[1-3]。目前，视觉设备的安装平台分为固定平台和移动平台两种，具有应用局限性，移动平台一部分以电机驱动，可以实现左右摇摆和上下俯仰2 自由度的转动，如监控探头[4-5]；另一部分，在“eye-in-hand”视觉系统中，视觉设备跟随机械臂末端运动，实现空间运动[5-8]，稳定性不好。并联机构具有刚度重量比大、稳定性强和环境适应性强等优点，而且响应速度快、技术附加值高、易于重构并且制造成本低[9]，因此，并联机构平台得到了广泛地关注。文献[10-12]以3-RRR 并联机构为平台设计了球面并联机构仿生眼。3-RRR 并联机构能实现绕三个轴的转动[13]，但在工业生产中很少应用。文献[14]开发了基于3-RPS 并联工作台的新型3D 打印机构，在满足3D 打印技术的基本成型条件的同时，还能够完全按照纤维取向成型。文献[15]研制了一台基于3-RPS 并联机构平台的灭火喷枪样机，实现了远程无人灭火。文献[16]将 3-RPS并联机构应用于先进机床。文献[17]提出了一种3-RPS 机器人和虚拟现实技术结合的全新滑雪模拟器方案，可以模拟滑雪者俯仰、偏转，速降 3个维度的运动。

3-RPS 并联机构是在Stewart 六自由度并联机器人的基础上发展而来的[18]。通过改变三个移动副的位移使动平台可以实现前后移动、左右摇摆和上下俯仰3 个自由度[19]。将视觉设备安装于该平台上，能够实现在机器人本体位姿或目标本体位姿不变的情况下，视觉设备能够到达满足拍摄要求的角度和位置，从而获取高质量的图像或视频，为后续的图像处理提供方便。本文对视觉设备安装平台进行建模，并基于MATLAB 对其工作空间进行分析，该平台的工作空间大，运行稳定性好，具有较高的实用价值。

1 视觉设备安装平台的建模分析

1.1 视觉设备安装平台的自由度计算

自由度的表达和计算是机构研究很重要的一部分，只有对机构自由度正确的分析、计算与表达，才能得到相应的机构，并且能够实现真实的运动。

其中，F 为机构的自由度，n 为构件数，g 为运动副数，fi为运动副的自由度，d 为机构公共约束因子，d= 6 - λ，λ 为机构公共约束数，ν 为并联冗余约束因子。3-RPS 型并联机构平台为3 自由度的空间机构。

1.2 视觉设备安装平台的建模

在分析机构的工作空间时需要建立机构模型，各结构设计合理才能完成仿真[20]。利用SolidWorks 对视觉设备安装平台进行建模，如图1 所示。视觉设备的光轴线交于动平台平面的形心点，视觉设备底面与动平台平面贴合。机构的主要参数如表1 所示。

表1 3-RPS 并联机构的主要参数 Table 1 Main parameters of 3-RPS parallel mechanism

图1 视觉设备安装平台模型 Fig.1 Visual equipment installation platform model

2 平台机构运动学分析

2.1 平台机构描述

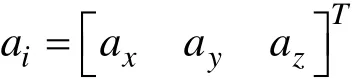
图2 视觉设备安装平台简图 Fig.2 Visual equipment installation platform sketch

定坐标系位于静平台的几何中心，动坐标系位于动平台的几何中心，初始位置时，动平台平行于静平台，当动平台绕着动坐标旋转时，动平台的位姿发生改变，为了确定动平台在运动中相对于定平台的位置，根据3-RPS 并联机构的运动特点，采用欧拉角来描述。

2.2 视觉设备安装平台的运动学正解

如图2 所示，设 φi（ i = 1,2,3）为支杆 AiBi和基座OAi的夹角。例如，在固定坐标系下球关节 Bi的位置向量可以表示为：

将式（2）~（4）代入式（5）可得：

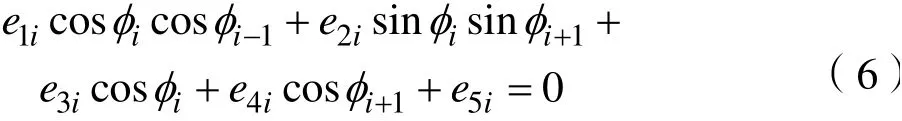
球关节iB 对于定平台的位置向量2q 也可以写成：

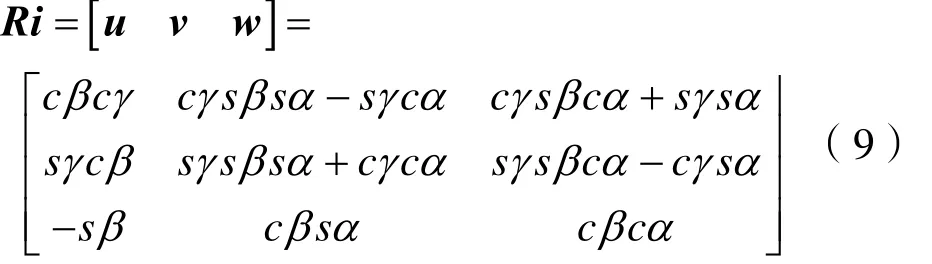
因此，

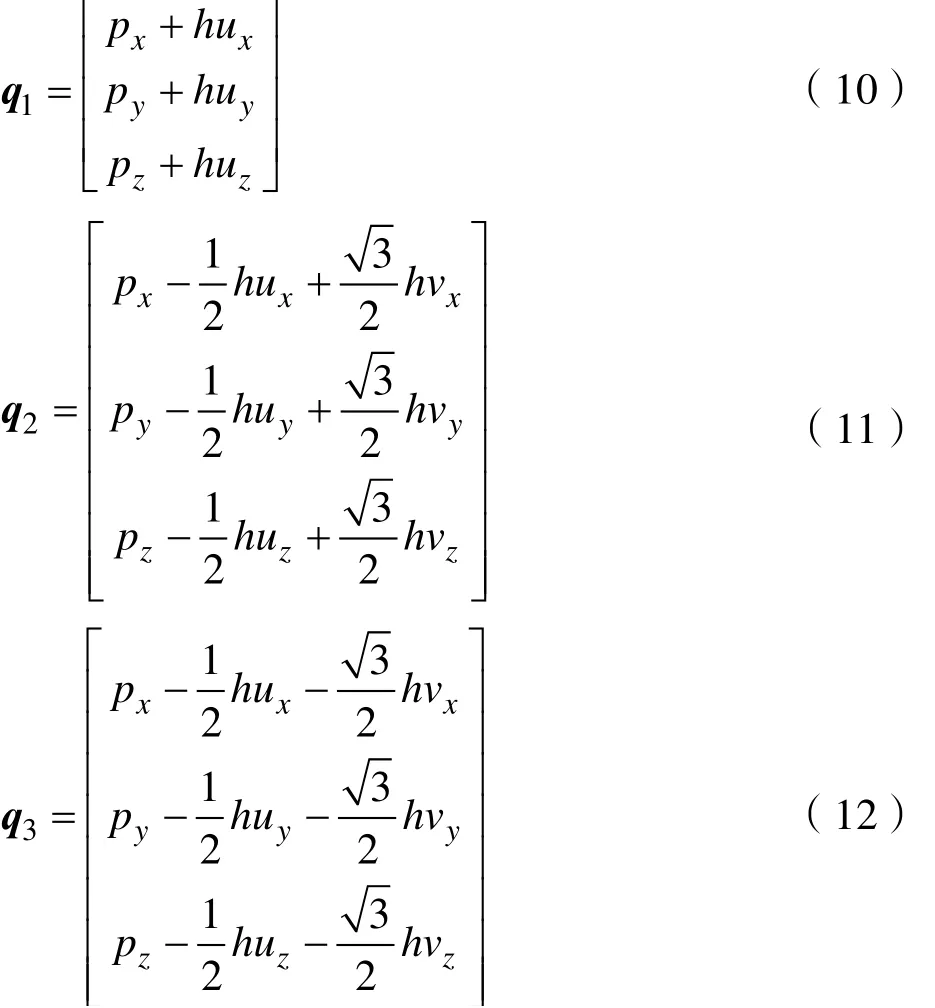
通过式（9）~（12）可以求得Z-Y-X 型欧拉角，如下式：

2.3 视觉设备安装平台的运动学逆解

如图2 所示，动坐标相对与定坐标的旋转变换矩阵为：

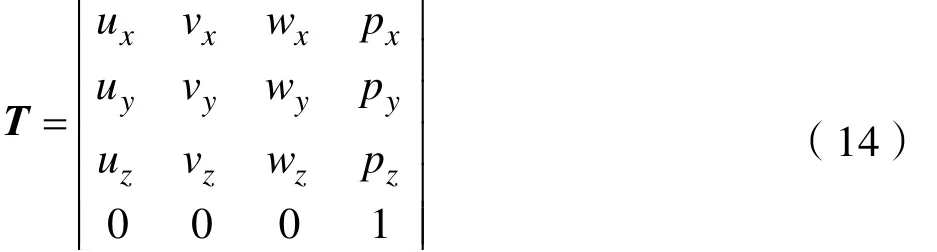
其中，点P 为上平台形心。因此，在定坐标系O-XYZ 中， Bi（ i= 1,2,3）的坐标为： 机构各部分普遍存在约束条件[22]。当3-RPS 并联机构基面内转动副的轴线对中心点O 呈切向分布时，机构 3 个分支转动副的这种位置布置限制了动平台3 个球铰的运动。 B1, B2,B3三点必须在 y=0,y=x,y=-x3 个垂直平面内运动，如图3 为三个约束平面。

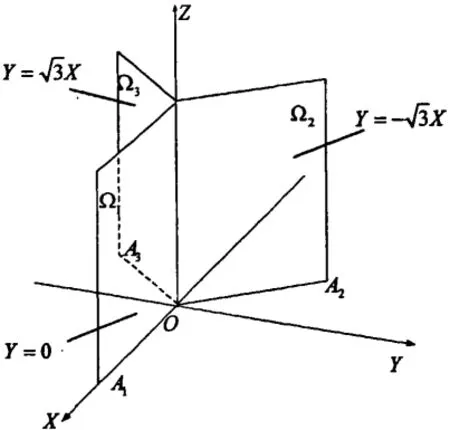
图3 约束平面 Fig.3 Constrained plane

因此，可得:

设动平台相对于定平台的空间Z-Y-X 欧拉角表示为（γβα），则转换矩阵为：

求得：

这样矩阵T 中就只含有α 、β 和 pz3 个变量。动平台铰链点 Bi（ i= 1,2,3）相对于静坐标系O-XYZ的表达式为：

式（22）是关于α 、β 和zp 的表达式，只要给定机构动平台的姿态参数α 、β 和动平台P 点的高度zp 就可以计算出连杆的长度。经过平台机构的运动学分析，可以明确得到机构各关节量与平台位姿之间的对应关系[21,22]。

3 视觉设备安装平台的工作空间分析

3.1 视觉设备安装平台的工作空间分析

将动平台的形心定为参考点，其可能达到的某一空间定为搜索空间。首先将动平台的工作空间用平行于p-xyz 面的平面分割成若干个厚度为 zΔ 的子空间，在给定动平台形心在定平台坐标系Z 方向的坐标值的情况下，使动平台进行2 次转动，然后在物理模型中找到形心的坐标，视为一个边界点。将收集到的所有边界点的坐标，用MATLAB 软件进行编程，得到整个动平台的工作空间，如图4 所示。

3.2 支杆伸长量与欧拉角之间的关系

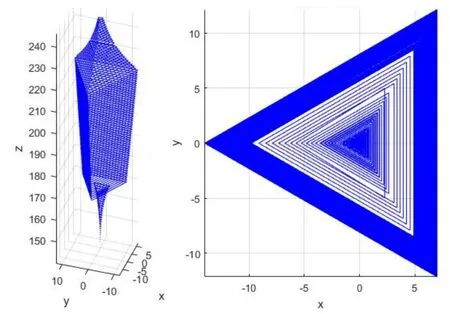
图4 视觉设备安装平台的工作空间 Fig.4 The workspace of visual equipment installation platform

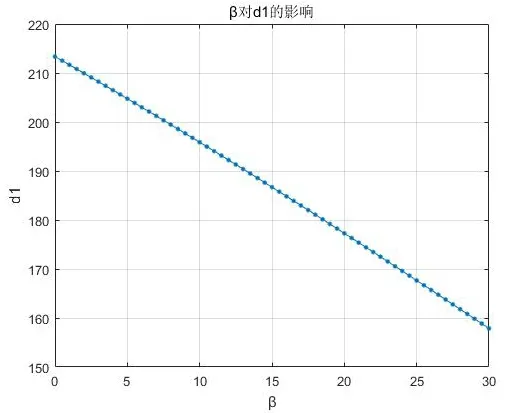
图5 杆长 1d 与β 角的关系 Fig.5 Relationship between 1d and β

影响机构姿态的因素有很多，欧拉角对机构姿 态是主要的影响因素。设欧拉角β 的范围为0 ~30° °， 0α = °。支杆的伸长量与欧拉角之间的关系，如图5 所示。

图中可以看出随着欧拉角β 的增加，支杆1d 的长度基本趋于均匀减小；在 0β = °时，即动平台与静平台处于平行状态时，支杆的长度最长，这符合实际情况。

3.3 机构的输入输出关系

在已知了3-RPS 并联机构的工作空间的基础上，研究机构的输入输出关系是必要的。机构的输入输出关系可以间接的反映机构的工作性能与工作效率。本文从三个方面研究了机构的输入输出关系。

（1） 若动平台中心只沿着X 轴运动，则 py= 0，欧拉角的关系如图6 所示，机构在只沿X 轴运动时，其运动轨迹是关于Y 轴对称的。由图可以看出，当输入欧拉角α=0°, β= 0°时，输出的γ= 0°；

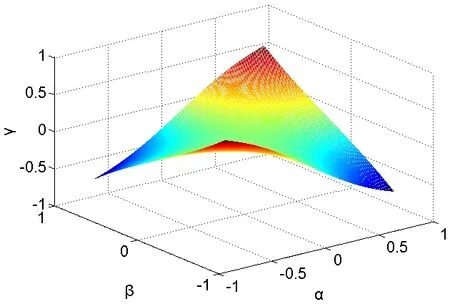
图6 py= 0时欧拉角关系图 Fig.6 Euler angle diagram when p y= 0

（2）若动平台只沿着Y 轴运动，则 px= 0，欧拉角的关系如图7 所示，机构在只沿Y 轴运动时，其运动轨迹是关于X 轴对称的。由图可以看出，当输入欧拉角α=0°, β= 0°时，输出的γ= 0°。

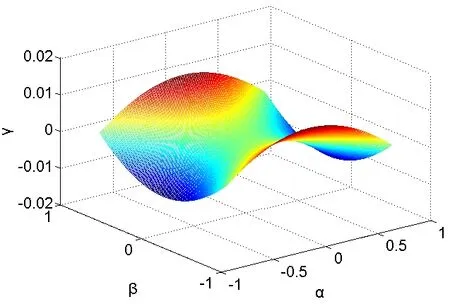
图7 px= 0时欧拉角关系图 Fig.7 Euler angle diagram when p x= 0

（3）若动平台中心维持在 Z 轴上，则px= 0, py= 0，欧拉角的关系如图8 所示。

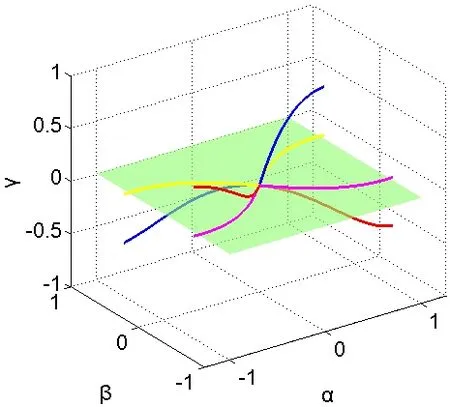
图8 px=0, py= 0时欧拉角关系图 Fig.8 Euler angle diagram when px=0, py= 0

由图9 可知，当动平台只沿着Z 轴运动时，则欧拉角的关系呈两条曲线分布，分布在 γ = 0°的平面两侧。当α=0 °,β= 0°时，动平台与静平台处于平行状态。当输入α=10°，则输出β= 10° 或β = 10° ； 当 输 入 β = 10°时， 输 出α= 10° 或α=-10°。欧拉角β 与γ 的关系与欧拉角α 与β 的关系类似，这也是符合实际情况的。

中心点P 的位姿可用向量w 表示，其中w 为：

则可求得向量的末端轨迹，如图9 所示。

图9 形心只沿Z 轴运动的轨迹图 Fig.9 Trajectory map of the centroid only along the Z axis

4 结语

本文针对目前串联机构的视觉设备安装平台工作空间受限，运行稳定性差等问题，基于3-RPS并联机构设计了一种视觉设备安装平台，基于MATLAB 对该平台进行了分析。经过对相关参数之间关系的分析，确定了并联机构的工作空间，该平台的工作空间大，视觉设备可以实现前后移动、左右摇摆和上下俯仰，且运行稳定性好。后期，需要搭建实验平台，并进行视觉设备安装平台的控制实验，对系统参数进行优化，促进该平台的实际应用。