基于多色集合理论递阶系统的网络化制造资源优化配置

刘晓阳 刘恩福 方忆湘 刘振宇 靳江艳

河北科技大学机械工程学院，石家庄,050018

0 引言

随着网络技术及信息技术的不断发展，为了应对知识经济和制造全球化的挑战,快速响应市场需求和提高企业竞争力，网络化制造成为制造企业发展的必然趋势[1]，而追求成本、时间与质量的最优制造资源配置是必需解决的关键技术[2]。目前针对该技术的研究总体上分为两大类：主观赋权评价法和客观赋权评价法[3]。主观赋权评价法由专家根据经验进行主观判断并采取定性的方法得到权数，如层次分析法、遗传算法等。文献[4-5]通过模糊层次分析法建立资源选择数学模型实现定性问题定量化，并进行多层次、多目标的优化选择；文献[6]构建了产品定制资源优化配置的双层规划数学模型，采用一种嵌入双层迭代规则的混合遗传算法对产品定制资源进行优化配置。客观赋权评价法权数的确定依据各项指标的变异系数或指标之间的相关关系，如灰色关联度法、TOPSIS法等。文献[7]采用基于改进优劣解距离的动态多属性决策方法对Pareto最优解所代表的互为非支配的制造云服务(MCS)组合方案进行评价排序，筛选出最优的MCS组合方案。

多色集合理论(theory of polychromatic sets，TPS)[8]是近年来先进制造技术领域中提出的重要概念和理论之一，它在系统建模、复杂层次结构和关系描述、问题的形式化表示以及高效的计算机处理等方面具有优势，愈来愈得到产品设计与制造领域相关研究人员的重视。

本文将TPS引入到制造资源优化配置过程中，通过建立TPS递阶系统，分层组织和管理数据，并将数据以布尔矩阵的形式存储，方便计算机进行表示、处理、编程并减少存储空间；通过TPS的形式化推理和逻辑运算，实现制造资源给定目标或多目标评估的优化配置。

1 多色集合的模糊数学模型

1.1 多色集合

多色集合信息模型是由多色集合元素、个人颜色、个人着色、统一颜色和统一着色及其相关关系组成，以布尔矩阵形式进行信息存储的数学模型。本文采用的多色集合理论数学表达式为

PS={A,F(a),[A×F(a)]}

(1)

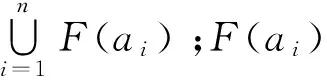
[A×F(a)]=‖cij‖A,F(a)

(2)

式(2)中，元素ai的个人着色F(ai)由第i行元素cij=1的个人颜色确定。

在使用多色集合时，通常用围道的概念来替换术语颜色，围道即为性质、属性、参数、特征、指标等技术概念的抽象和概括。

1.2 多色图

在多色集合中，多色图是其图示化的重要工具，多色图由三种成分组成：

PG={F(G),PSA,PSC}

(3)

式中，F(G)为多色图整体的统一着色；PSA为节点的多色集合；PSC为边的多色集合。

1.3 多色集合的模糊数学模型

1.3.1模糊围道关系

传统多色集合理论的布尔矩阵是一个二元布尔矩阵，元素值只有0(没有关系)和1(有关系)，是一种简单的关系描述矩阵[9]。而在制造资源配置过程中，制造任务与制造资源围道之间的关系存在不确定性：

(1)制造资源参数值存在不确定性,这将导致制造任务与制造资源匹配关系的不确定性。制造资源指标参数可能是一个准确值，也可能是一个区间值，如制造资源的加工精度、加工范围等，当制造资源指标参数为区间值时，制造任务与制造资源围道之间可能会完全匹配、不匹配或部分匹配，如果是部分匹配，有可能满足匹配要求，也可能没达到规定指标不满足匹配要求，因此，制造任务与制造资源之间存在着非确定性的匹配关系。

(2)资源配置集合中元素(围道)组成存在不确定性。

1.3.2模糊信息表达

为了满足制造资源配置建模以及资源配置过程的需求，对传统的多色集合理论作以下改进。

(1)针对制造资源参数值的不确定性导致制造任务与制造资源之间的映射关系存在不确定性，建立cij∈[0,1]的模糊布尔矩阵。

(2)针对多色集合中元素间及围道间的关系及联系的不确定性，建立模糊集合和普通集合元素间及围道间的对应关系：

(4)

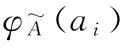
(5)

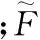
2 TPS递阶系统

制造资源配置是从零件信息模型开始的，由工艺人员对零件图纸和零件制造工艺进行分析，将零件的生产过程分解为若干个制造阶段；利用离散的制造资源，通过任务单元与制造资源一定的属性映射，获得满足任务单元制造能力要求的制造资源，并以时间、成本以及质量等定量指标作为优化目标，进一步对制造资源进行多目标的优化，组合一条最优的加工路线。

定义1任务单元根据零件加工工艺信息形成的、以典型几何特征及加工要求为元素的加工单元集合，它是特定加工特征及加工要求的宏观描述[2]，用t表示，其属性可以用9维的特征向量表示：

t=(t_pf,t_f,t_ma,t_r,t_d;
t_of,t_mach,t_pre,t_pro)

(6)

式(6)分为两部分：①零件信息部分,即t_pf表示零件类别，t_f表示制造特征类型，t_ma表示材料类别，t_r表示毛坯类别，t_d表示尺寸范围；②主要的工艺信息部分,即t_of表示组成加工单元类型，t_mach表示加工方法，t_pre表示加工精度类型、t_pro表示生产类别。

本文借助多色集合的形式化表达和逻辑推理建立TPS递阶系统，如图1所示，该系统分为递阶关系层和递阶推理层。递阶关系层负责组织和处理信息，描述制造任务、配置资源与评价指标之间及其属性之间的逻辑关系，满足递阶推理的需求，利用TPS对信息之间的逻辑关系进行形式化表达，并以布尔矩阵的形式进行存储；递阶推理层进行数据计算和优化，按照零件工艺流程对制造资源进行多目标优化，达到制造资源优化配置的要求。

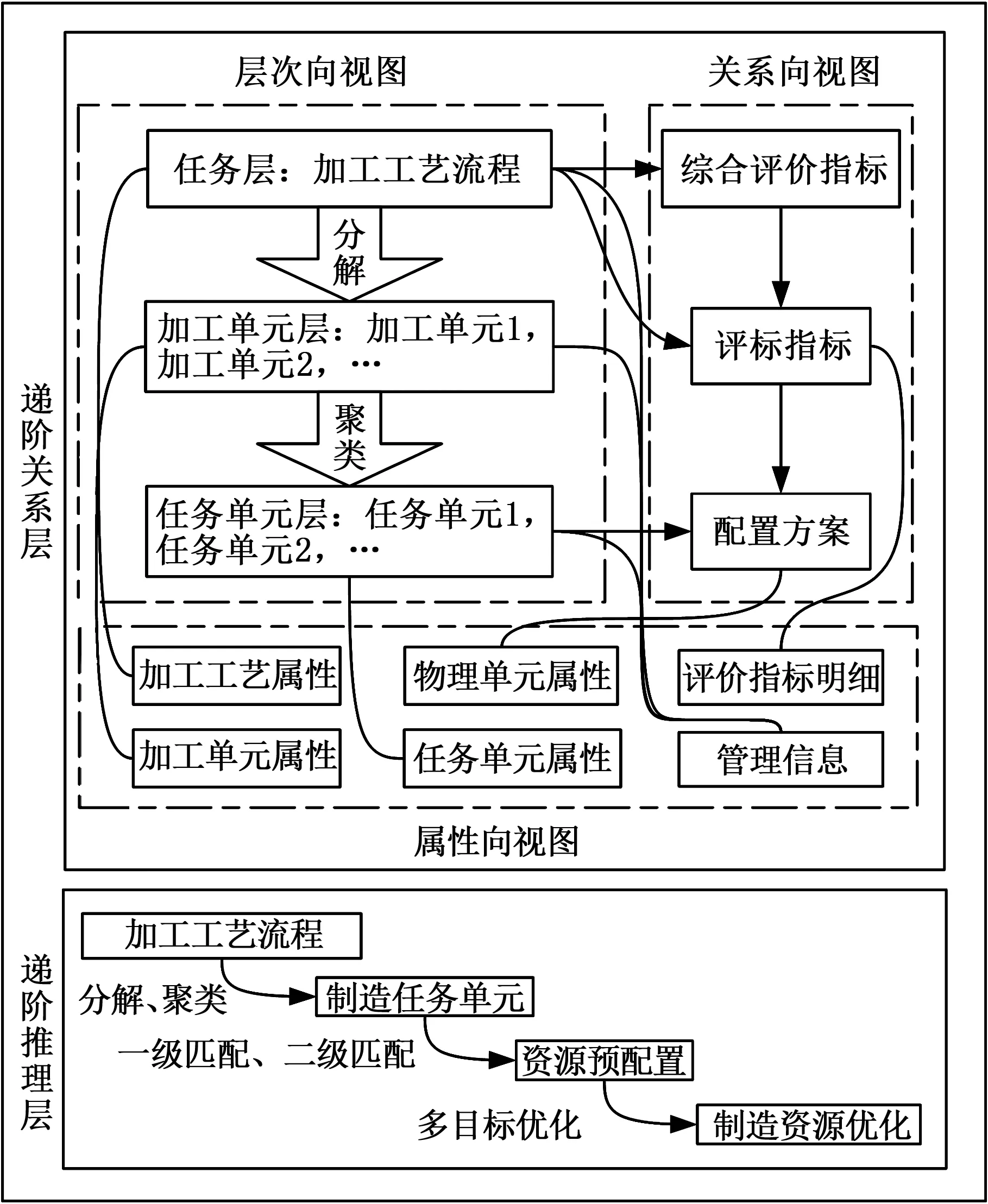
图1 TPS递阶系统结构Fig.1 The structure of TPS hierarchical system

3 递阶关系层

递阶关系层采用多视图的表达方法，即层次向视图、属性向视图和关系向视图。层次向视图的各层属性从属性向视图中提取，而属性向视图中属性的关联关系从关系向视图中提取；属性向视图中的属性信息要通过层次向视图和关系向视图中的具体内容来承载；关系向视图的生成可以根据层次向视图各层次属性关联匹配而得到。图1中，递阶关系层中各向视图之间相互联系，使制造资源配置过程在一个模型中加以综合运算，以支持制造资源配置各环节的顺利进行。

3.1 任务的多色图表达

运用图论的思想，任务单元可以抽象为图的节点，但是，传统图论工具不可能既描绘图节点和边的组成，又描绘图的节点和边所具有的不同性质[9]。本文利用多色图的概念建立制造任务PG的多色图

PG={PST,PS(T×T)}

(7)

3.1.1多色集合PST

多色集合PST描述多色图所有的节点、节点属性及节点与属性之间的关联关系，形式化表达为

PST={T,F(T),[T×F(T)]}

(8)

式(8)中，T表示任务单元集合；ti为制造任务中的第i个任务单元，任务单元ti∈T；F(ti)为任务单元ti对应的个人着色，表示任务单元的加工指标信息属性，其形式化表达为

(9)

3.1.2多色集合PS(T×T)

多色集合PS(T×T)描述任务单元在按照工艺流程完成过程中彼此之间存在一定的联系和信息依赖关系，其形式化表达为

PS(T×T)={[T×T],[(T×T)×F(T)]}

(10)

式中，围道矩阵[T×T]为任务单元的自相关围道矩阵，描述任务单元间信息传递的路径、方向；[(T×T)×F(T)]表示任务单元间的连接形式。

自相关围道矩阵[T×T]表示任务单元集合T与其自身的笛卡儿积，其形式化表达为

[T×T]=‖τij‖T,T

(11)

其中,τij表示任务单元间信息依赖程度的逻辑值，当任务单元间有确定的连接关系时，τij使用布尔数值0(没有关系)和1(有关系)表示，否则τij∈(0,1)，即定量表示任务单元ti依赖于任务单元tj信息输入的程度。

围道矩阵[(T×T)×F(T)]是任务单元的自相关矩阵，定义多色集合的元素为任务单元ti和tj的两两组合，定义多色集合的围道Fk(ti,tj)为任务单元ti和tj之间可能的连接关系，即连接弧、与分、与合、或分和或合，连接关系及对应符号如表1所示。

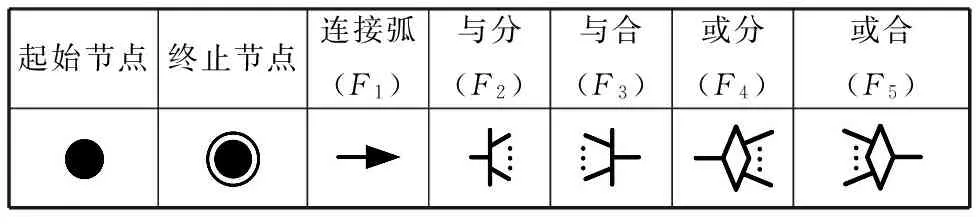
表1 连接关系及对应符号

任务单元可表示零件加工过程中多个不同且不连续的加工阶段，因此，通过任务单元之间存在一定的信息依赖关系可将各任务单元连接起来，连接形式如表2所示,归纳以下3类：

(1)顺序形式。任务单元之间有先后顺序的约束，即上游任务单元要先于下游任务单元完成。

(2)并列形式。任务单元之间能够同时或以任意次序独立执行，相互间无信息交换，互不影响。

(3)耦合形式。任务单元之间存在双向的信息交换，即任务单元ti需要任务单元tj的输出信息作为输入，同时任务单元tj需要任务单元ti的输出信息作为输入。耦合连接形式可分为耦合形式①和耦合形式②(迭代形式)。

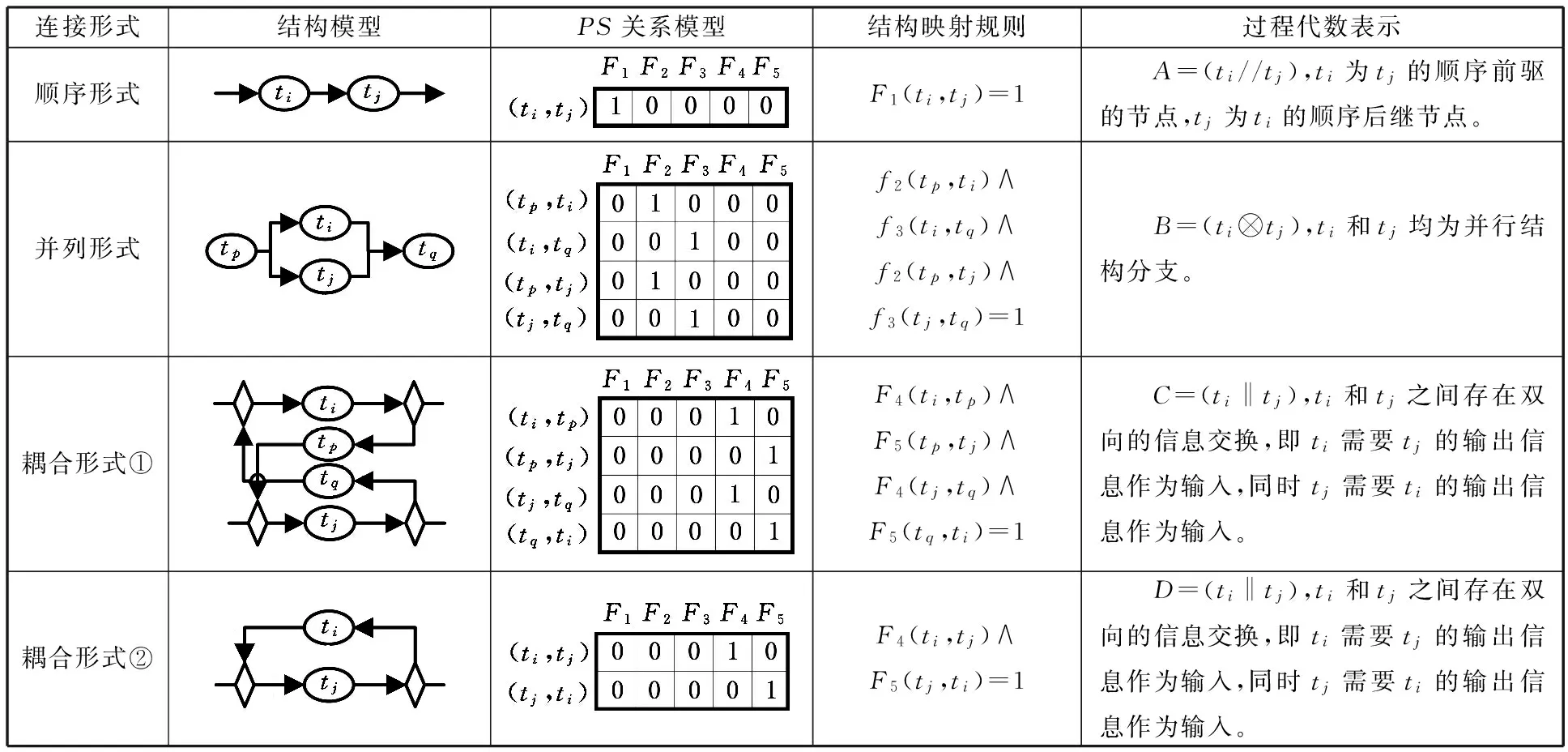
表2 任务单元连接形式及其形式化映射

3.2 映射关系的形式化表达

3.2.1评价指标体系的构建

通过对资源配置过程进行深入分析，将问题分解成4个层级，即目标层O、指标层A、B和方案层R(图2)。目标层O是最高层，为综合评价指标，最下层为配置方案层R，指标层A为制造资源的容错性指标，指标层B为优化指标层，图中存在关系的上下层因素之间用直线相连。

在配置方案层R，为了将分散在不同地方的制

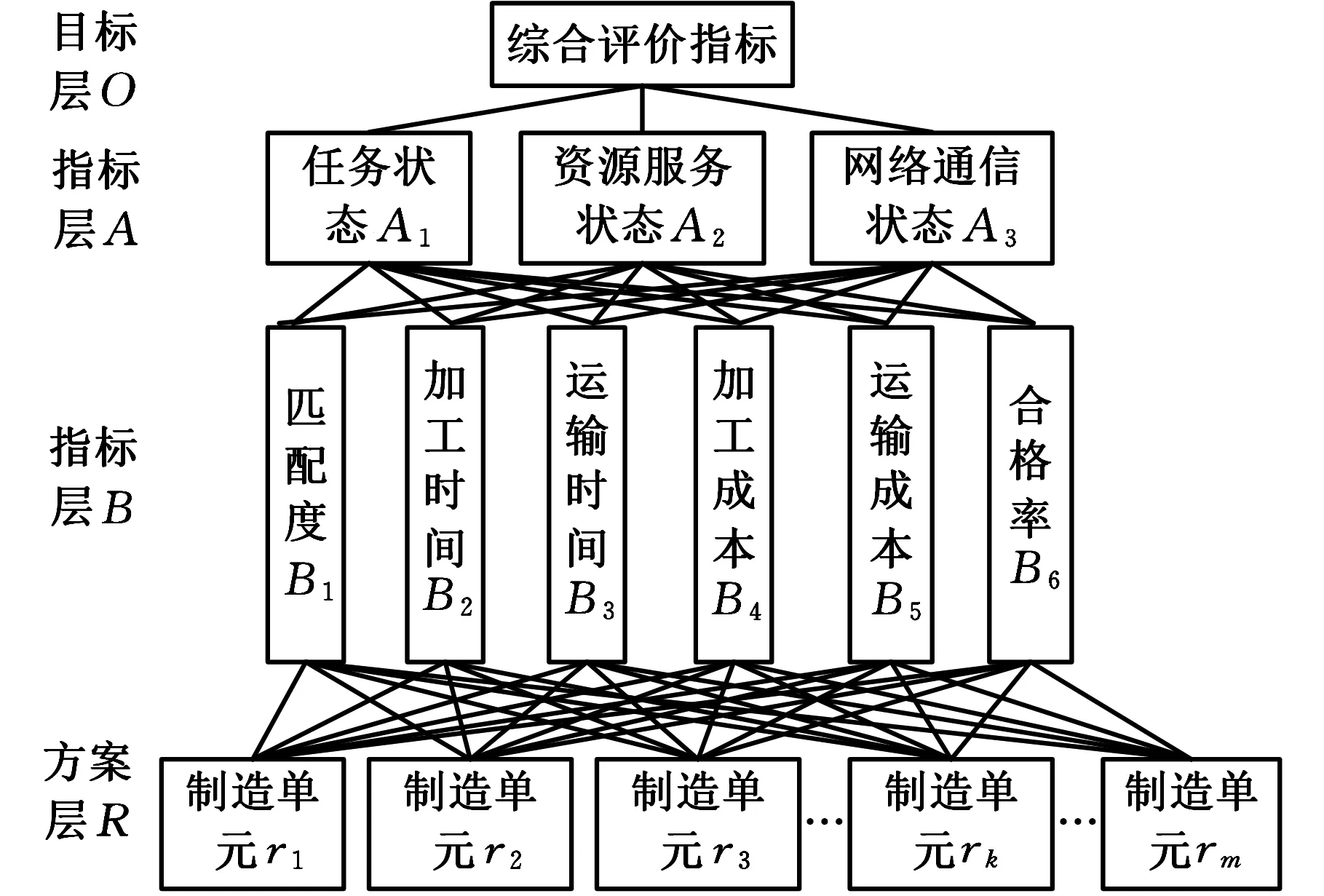
图2 资源方案评估层次结构模型Fig.2 The hierarchical model of resource scheme evaluation

造资源进行逻辑上统一管理，形式上统一表达为

PSR={R,F(R),[R×F(R)]}

(12)

其中，R={r1,r2,…,rk,…,rm}，rk为制造资源中第k个制造单元；m表示制造单元的数目；F(rk)为rk的个人着色，即描述rk的制造能力、设备与工装信息以及状态的属性，形式化表达为

(13)

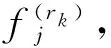
(14)

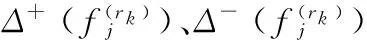
制造单元rk的个人着色F(rk)的并集为所有制造单元的个人着色F(R)。

3.2.2容错性

在资源配置的指标中，添加容错性指标。资源配置的容错即当配置过程中系统的某一部分发生失效时，通过失效监控进行废除或隔离，并将完好的资源介入系统，实现系统不停断的工作[10]。

通过在评价指标中增加网络通信状态、资源服务质量、资源服务状态、数据间的一致性、任务状态等指标，在资源匹配之前，进行预配置资源的容错性检查，保证资源配置的有效性和配置过程的连续性。本文利用多色集合的形式化表达对任务单元和制造单元的关键指标信息进行定量化表示，解决数据间的一致性问题，因此，数据间的一致性问题在综合评价指标中没有体现。

3.2.3综合权重计算

本文采用兼顾主观性和客观性的粗集-层次分析法计算权重。粗集理论是一种研究不完整数据和不确定知识的表达、学习及归纳的数学方法[11]。基于粗集理论的权重确定方法是一种依赖于客观事实的决策方法。

(1) 决策表。S=(U,R)为一知识表达系统，U是一非空有限集，称为论域；R是U上的一个二元等价关系，R∈U×U，也称为U上的属性集。 设R=C∪D(C∩D=∅),C和D是两个属性子集，分别称为条件属性和决策属性。具有条件属性和决策属性的知识表达系统可表达为决策表T=(U,R,C,D)。

(2) 区分矩阵。区分矩阵是一个普遍采用的知识约简方法。系统S=(U,R)，其中R=C∪D，r(x)是x在属性r上的值，区分矩阵M有n×n的维度，其中n表示基本对象的数目，而其单元定义为所有可识别基本集合{x}i与{x}j属性的集合，该集合中元素值计算公式为

(15)

当决策属性不同且条件属性也不完全相同时，元素值为互不相同的属性组合；当决策属性相同时，元素值为∅；当决策属性不同而条件属性完全相同时，元素值为-1，该情况表明数据有误或提供条件属性不足或某些属性为决策冗余属性。

根据区分矩阵可以构建区分函数f(R)：

f(R)=∧(∨cij)

(16)

若cij属性集合为空，则指定其为1。可辨识矩阵的定义表明：矩阵M中属性组合数为1的元素项的集合为粗集决策表的核。

(3) 属性的重要性：在区分矩阵M=[cij]n×n中，某个属性在区分矩阵M中出现的次数越多，以及所在的项越短，该属性越重要。相应的属性重要性计算公式为

(17)

式中，tij为cij中包含的属性的个数。

综合权重的计算公式为

wi=aw1i+(1-a)w2i

(18)

式中，w1i为通过粗集理论所计算的指标i的权重；w2i为通过层次分析法[5]所计算的指标i的权重；a为线性组合权重中的权重系数。

4 递阶推理层

通过递阶推理方法将制造任务与制造资源进行逐级模糊匹配，剔除不满足配置要求的制造资源，保证配置资源的可行性和提高匹配效率。

4.1 任务分解

如何控制子制造任务粒度大小，同时遵循“弱耦合”、“工序集中”等分解原则，是制造任务分解的难点问题。本文采用“分解-聚类”的方法降低任务分解难度的同时，保证任务分解的合理性，分解过程如下：

(1)分解。遵循工序分散原则，按照加工工艺流程，将制造任务分解为以特征为核心的加工单元组成。

(2)聚类。遵循加工方法相似的原则，将加工方法相同但出于不同加工阶段的加工单元安排在同一个任务单元内，使得每一种任务资源只需要一种核心资源。

4.2 制造资源匹配

为了提高匹配效率，制造资源预配置过程采用多目标决策的两级资源匹配。

(1)一级匹配。将任务单元的确定属性(如主要特征类别、材料类别等)与制造单元的同名属性进行自动匹配，对制造资源进行初步筛选，缩小搜索空间和提高匹配效率。匹配过程中，遍历所有制造单元每个围道，判断其是否能够完成任务单元ti：

ηij=F(ti)⊗∧F(rj)

(19)

式中，F(ti)⊗为所实现的任务单元ti围道的集合，即目标围道集合，这里假设已经获取；F(rj)为制造单元rj的围道;ηij为一级匹配系数。

判断制造单元rj能够完成任务单元ti的条件为

(20)

(2)二级匹配。由于任务单元与制造单元部分围道间关系具有不确定性，故在尺寸精度、表面粗糙度等方面需采取同名属性模糊匹配。当任务单元围道位于制造单元围道所达到的上极限值时，需要较好的加工技能才能保证任务单元围道，因此，定义制造单元选择的合理性为0.8；当任务单元围道低于制造单元围道所达到的下极限值时，任务单元围道容易满足，但是经济性会差一些，制造单元被选择的合理性小于1；当任务单元围道位于制造单元的经济精度范围内时，制造单元被选择的合理性在[0.8,1.0]之间。

在一级匹配的基础上，根据上述原则，采用二级匹配系数μk(ti,rj)描述任务单元ti与制造单元rj围道间的模糊匹配关系，其表达式为

(21)

式中，fk(ti)为任务单元围道的第k个值，fk(ti)∈F(ti);Δ+(fk(rj))、Δ-(fk(rj))分别为制造单元围道的第k个上极限值和下极限值。

定义2匹配度制造单元自身固有能力对于任务单元制造能力要求的适合程度。

本文通过引入函数φ(τ)计算匹配度，其中，τ为任务单元和制造单元的围道空间点之间的距离。制造单元ti与制造资源rj之间的距离τ通过映射规则F(ti,rj)比较围道F(ti)、F(rj)的组成来确定，而围道F(ti)与F(rj)以布尔矩阵形式存储，主要以二进制编码的形式表达，因此，把修正过的海明距离作为两者距离τF(ti),F(rj)，简写为τij，τij等于围道F(ti)与F(rj)二级匹配系数的连乘积，即

(22)

式中，L为匹配围道数目。

匹配度函数

φ(τij)=ηijτij

(23)

4.3 资源优化配置

通过设定时间、质量以及成本等优化指标和权重，对制造单元进一步优化选择，设R={r1,r2,…,rn},R为满足某制造任务需求的由N(N≥1)个制造单元组成的一种组合序列，优化配置目标是找到一个最优的制造单元组合序列R*，在满足质量要求和匹配要求的前提下，尽量缩短工期和降低成本。因此，给定目标和多目标优化函数：

(24)

式中，w1、w2、w3、w4、w5、w6为各个详细评价指标的权重；fc为制造单元的加工成本；ci为制造单元内在的加工成本；ci,i+1为相邻制造单元间的运输成本；ft为制造单元所需加工时间；ti为制造单元所承诺的加工时间；ti,i+1为相邻制造单元间的运输时间；fq为制造单元的平均加工质量；qi为制造单元加工零件的合格率，即为制造单元所承诺的加工质量；fφ为配置制造单元的匹配度。

制造资源多目标优化的数学模型为

(25)

5 应用实例

某企业接到变速箱体的订单，批量为50件，加工时间经过计算估计为50d，总的加工成本不超过4万，其工艺流程如图3所示，需要多台加工机床(包括传统的机床和数控机床)完成。考虑企业的制造能力和经济效益等，订单需要和其他企业协同完成。

5.1 制造任务分解及其形式化表达

根据变速箱体的工艺流程，由工艺人员分解成31个加工单元，并进行聚类和整合,最终分解为7个任务单元。

任务单元的完成过程如图4a所示，根据任务分解结果建立围道矩阵[(T×F(T)]，如图4b所示，任务单元的自相关围道矩阵[T×T]如图4c所示，建立围道矩阵[(T×T)×F(T)]，进一步确定任务单元之间的连接形式，以顺序连接和弱耦合形式为主，如图4d所示。图4将任务单元的关键指标信息定量化表示，保证了匹配对象数据间的一致性，避免因为数据类型不一致而导致匹配失效。

5.2 匹配度计算

(1)按照任务单元的执行过程，对 “制造特征”、“加工方法”、“负荷状态”等因素进行资源预配置的一级匹配，筛选掉ηij=0的制造单元。满足一级匹配的制造单元用r1，r2，…，r10表示，这些制造单元所承诺的加工成本C*、加工时间T*、加工质量Q*如表3所示，制造单元间的运输时间/运输成本如表4所示。

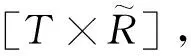
5.3 权重计算

(1)基于粗集的权重w1i的计算。选择匹配度、加工时间、运输时间、加工成本、运输成本、合格

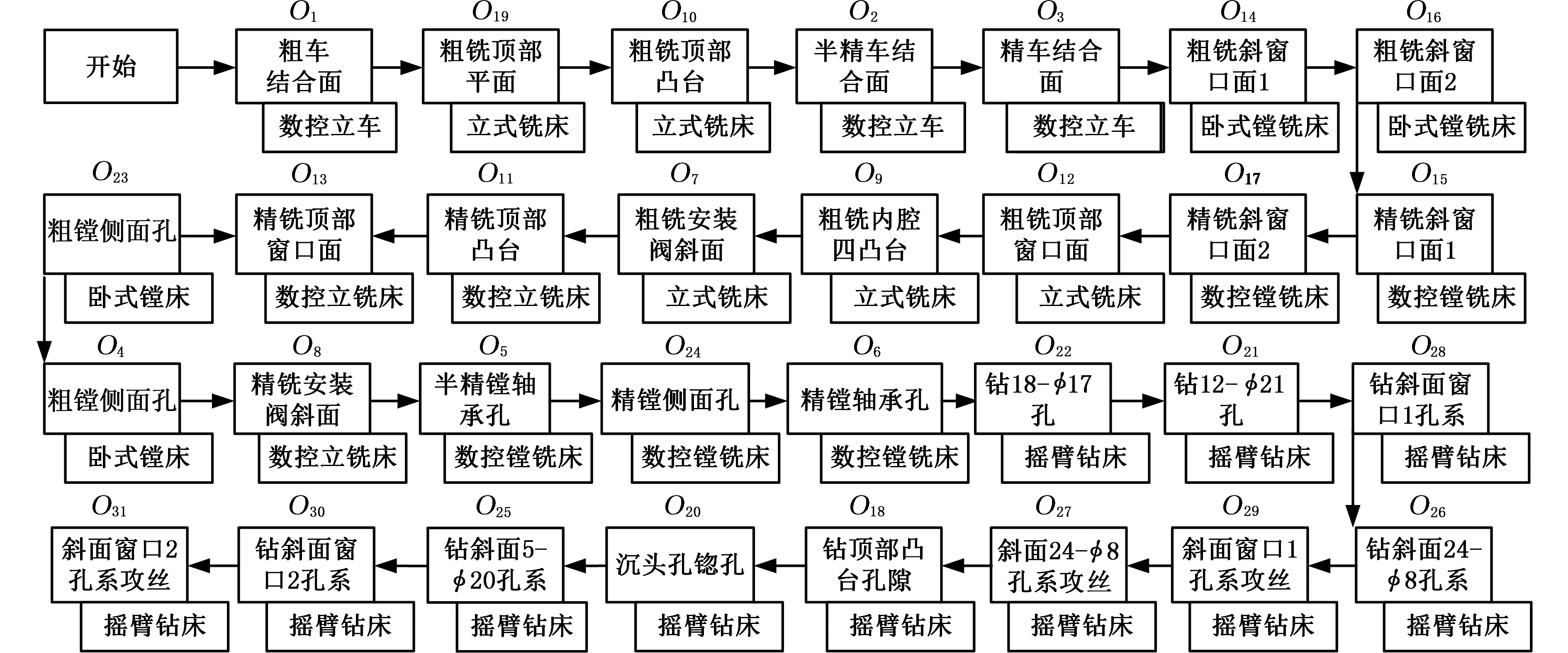
图3 某变速箱体工艺流程Fig.3 Process flow of gearbox

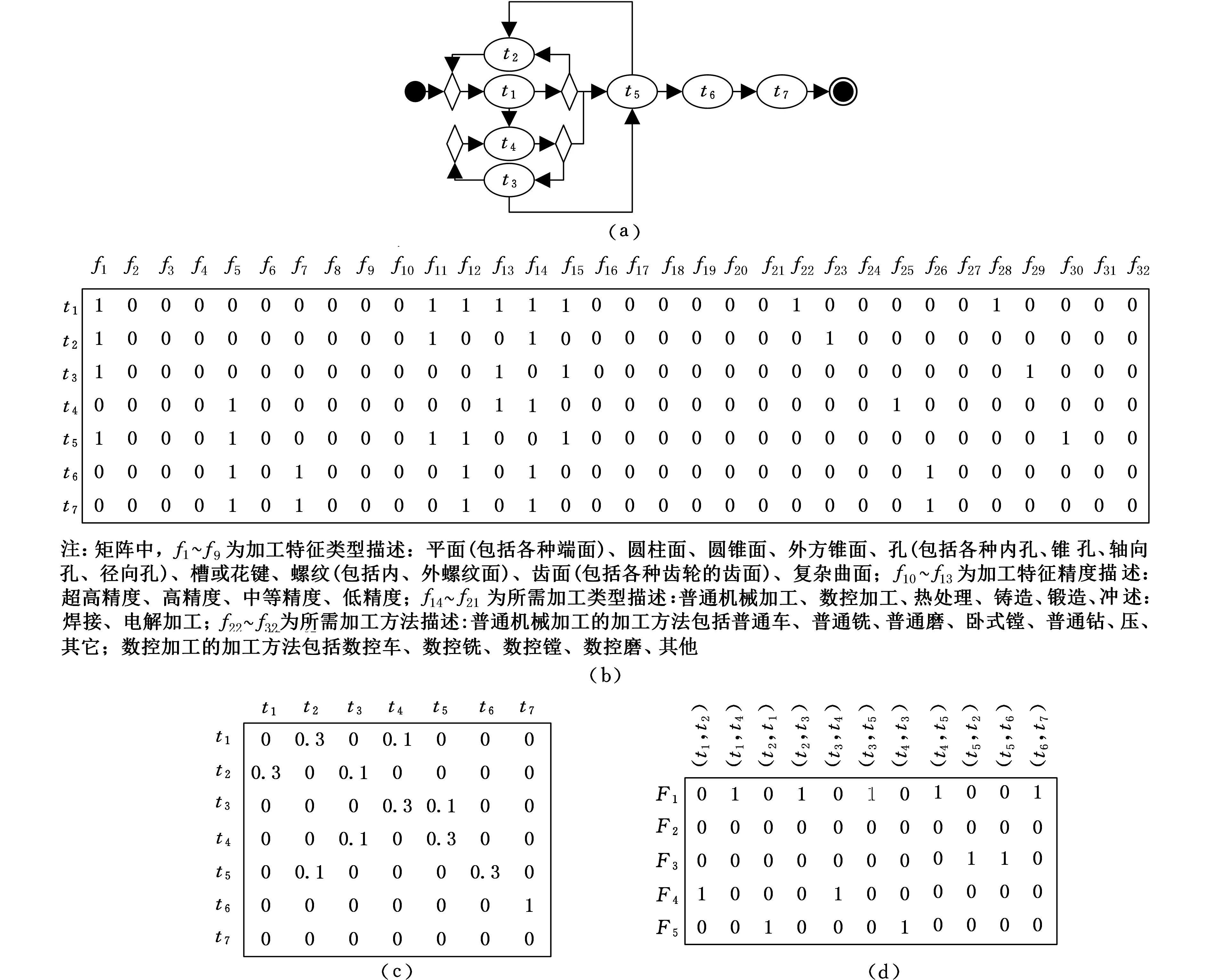
图4 制造任务的形式化表达Fig 4 The formal expression of manufacturing task

率为权重计算的评价指标。确定基于粗集所定的权重系数在最后线性组合权重中的权系数a=0.6。经过一级匹配后，确定10个匹配方案，并且具有以下特征：

a.所有预配置资源都满足给定的匹配度要求，即φ≥0.8。定义：φ≥0.9，表示匹配度高；0.8≤φ<0.9，表示匹配度低;如果有预配置资源对应多个匹配度，求均值。

b.定义合格率：Q*≥0.9，表示合格率高；Q*<0.9，表示合格率低，如果有预配置资源对应多个合格率，求均值。

c.决策属性D的高低受条件属性的影响，如果超过两项及以上的条件属性为低，那么决策属性为低，否则，决策属性为高。

表3 匹配制造单元所承诺的加工成本C*、加工时间T*、加工质量Q*

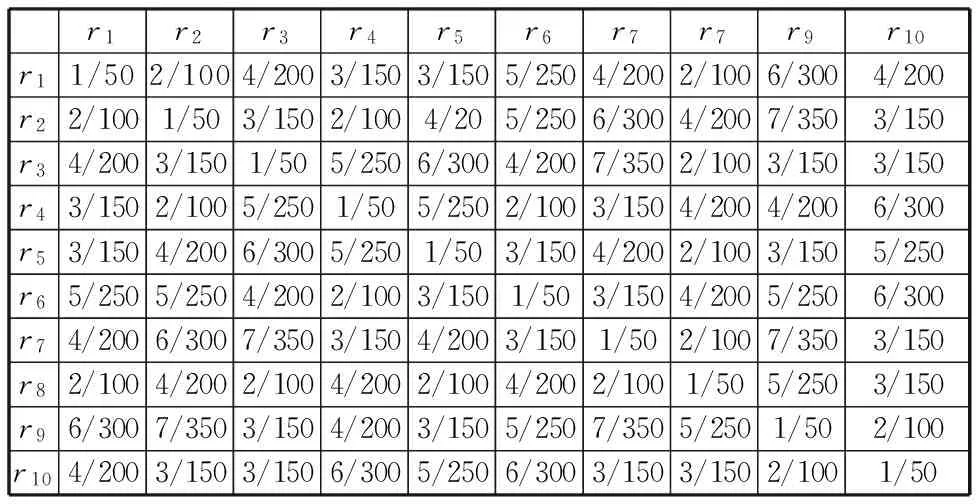
表4 匹配制造单元之间运输时间/运输成本

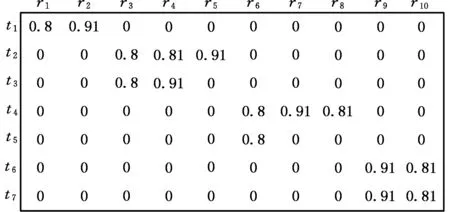
图5 模糊围道矩阵Fig.5 Fuzzy contour matrix

d.除上述评价指标外，其他指标值越大，条件属性越低，指标值越小，条件属性越高；条件属性的高或低须由工艺人员一致认可。确定条件属性的属性值是： 0表示低，1 表示高。 决策属性的属性值0表示低，1表示高。建立决策表(表5),构建区分矩阵M(图6)。

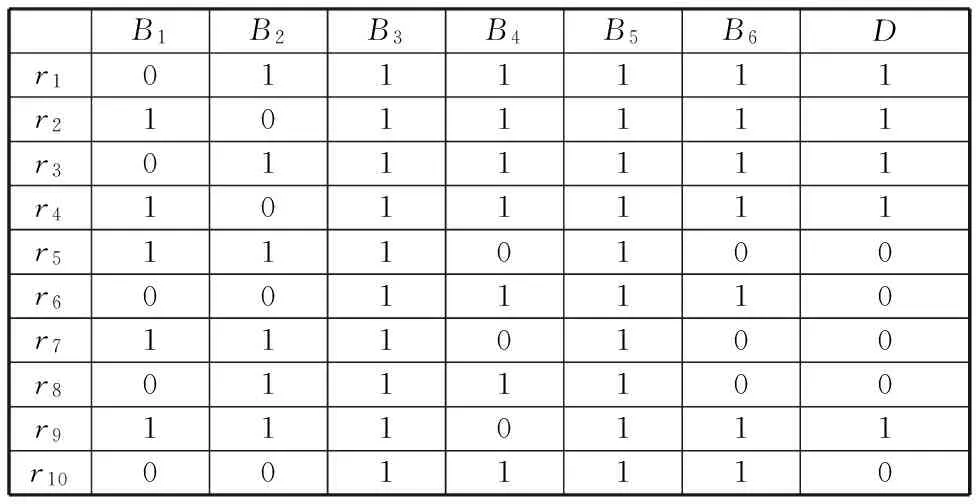
表5 决策表

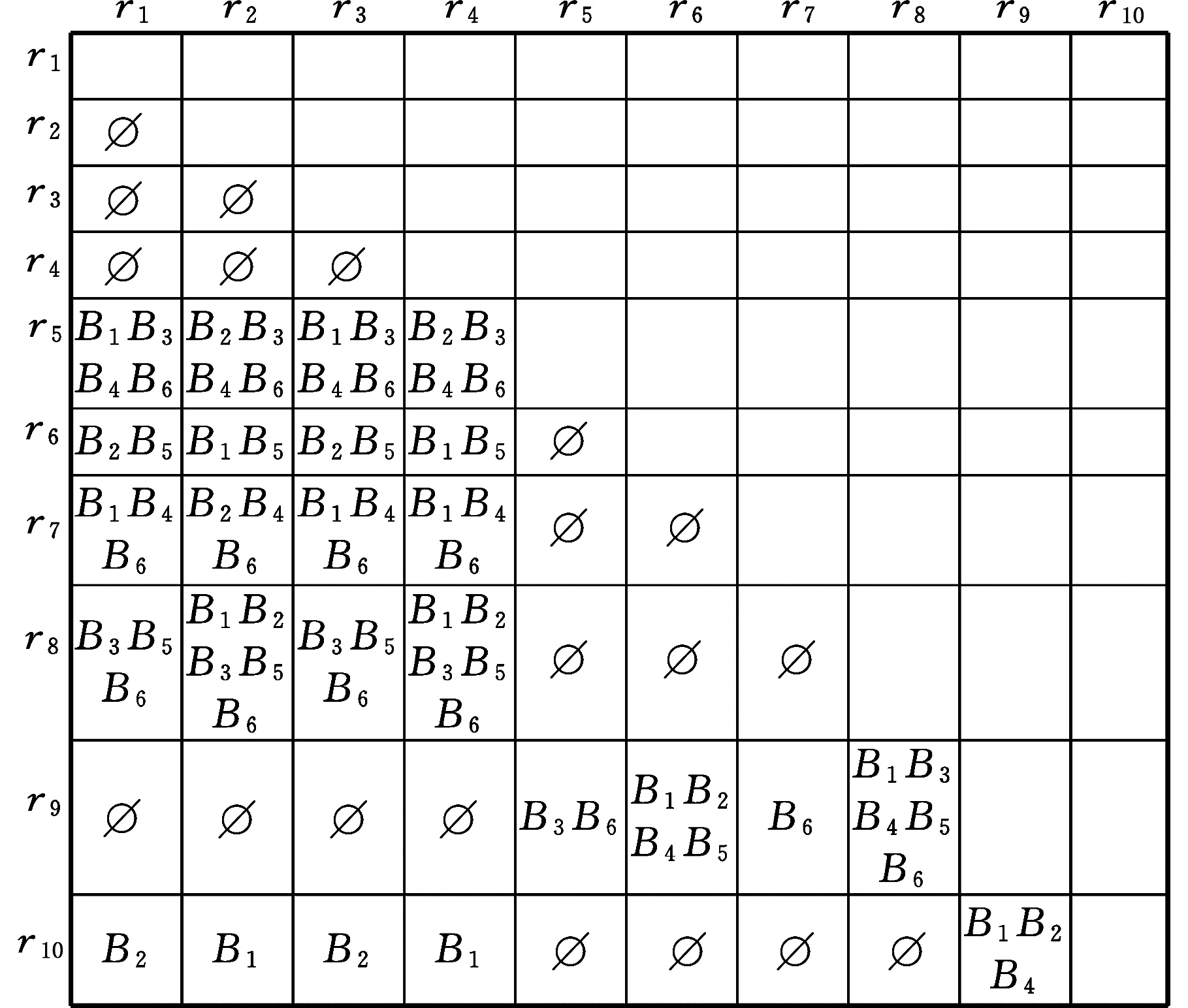
图6 区分矩阵Fig.6 Discernible matrix

按照式(17)，各指标属性重要性计算如下：f(B1)=5.35；f(B2)=5.15；f(B3)=2.77；f(B4)=3.12；f(B5)=3.52；f(B6)=5.1。

将各个属性的重要度进行归一化处理，得到客观权重如下：w11=0.214；w12=0.206；w13=0.111；w14=0.125；w15=0.141；w16=0.203。

(2)基于层次分析法的权重w2i的计算。根据制造任务要求，建立判断矩阵：

B1B2B3B4B5B6

最大特征值λmax=6.169 2，一致性指标CI=6.169 2，相容度CR=0.027 3<0.1。计算归一化权重w21～w26为：w21=0.080 6；w22=0.340 4；w23=0.037 6；w24=0.340 4；w25=0.037 6；w26=0.163 4。

(3)综合权重的计算。按照式(18)计算得到组合权重值分别为：w1=0.161；w2=0.259；w3=0.082；w4=0.211； w5= 0.10；w6=0.187。

5.4 资源优化配置

依据权重计算和匹配度计算的结果，根据式(24)以及表3和表4，对制造任务执行过程中的配置资源进行多目标的优化选择，优化配置结果如图7所示。

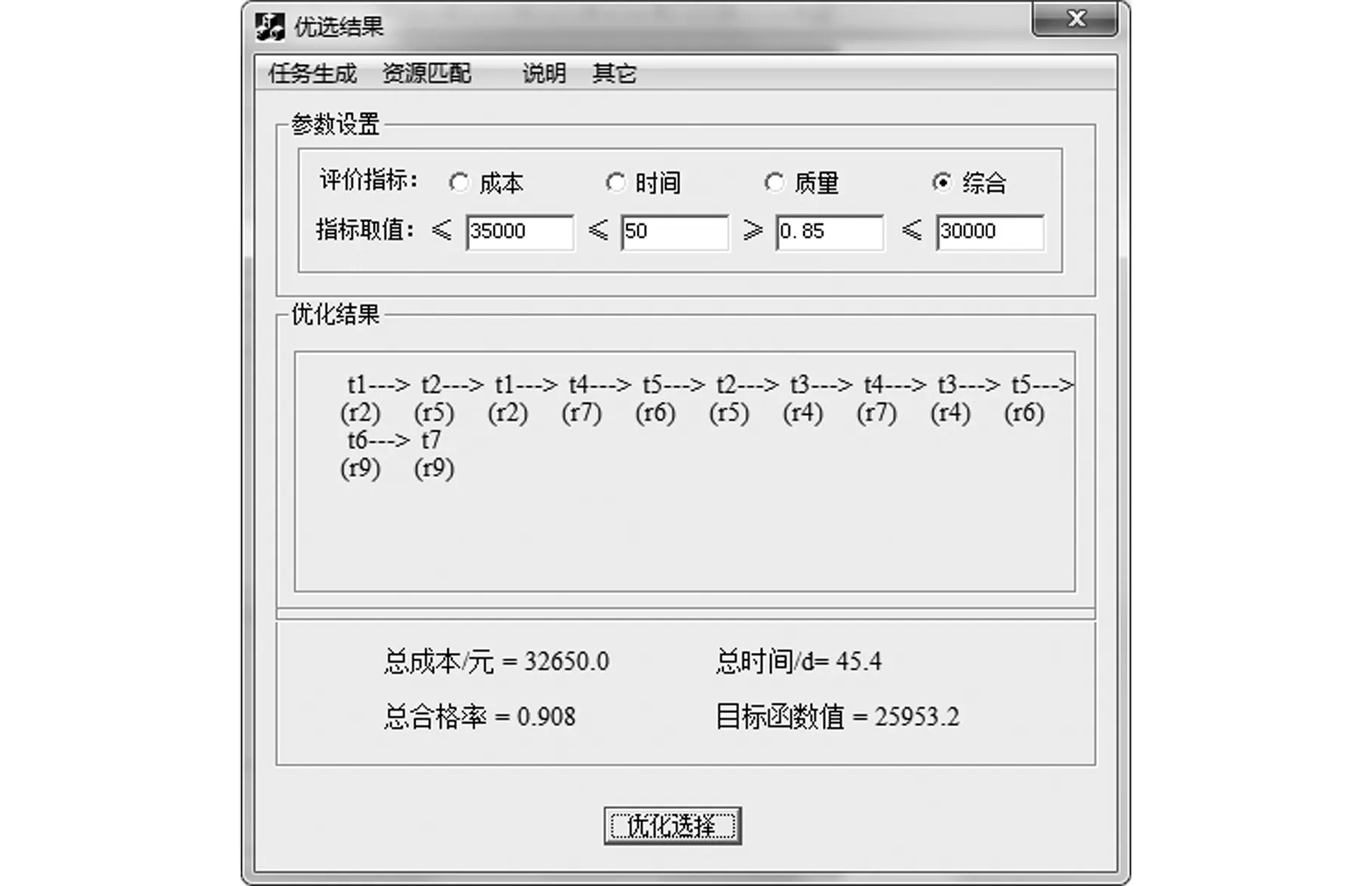
图7 某变速箱箱体资源优化配置结果Fig.7 The result of the gearbox manufacturingresources optimization deployment

整个配置过程中，实现了制造任务的形式化表达，并综合考虑时间、成本、质量以及制造资源的制造能力(匹配度)等关键指标完成资源配置，其中，任务完成总成本是32 650.0元，总时间是45.4天，合格率不低于0.908，最优目标函数值为25 953.2，各项指标都满足任务要求，尤其是成本远低于指定指标，获取最优的制造单元组合序列R*={r2, r4, r5, r6, r7, r9}。

6 结语

基于TPS递阶系统的网络化制造资源优化配置算法已应用在某煤矿机变速箱箱体的制造资源配置过程中，结果表明该算法实现效率高、结果合理，具有良好的应用价值，同时，此方法为资源优化配置提供了一种新的思路。

本文仍存在不足，如欠缺对制造资源状态的建模研究。今后研究将多色集合理论形式化推理与软计算方法相结合，考虑任务执行过程的并行性；完善评价指标，深入研究制造资源的容错性、可靠性等问题，提高资源配置的成功率，优化配置过程。

参考文献：

[1] 范玉顺. 网络化制造的内涵与关键技术问题[J]. 计算机集成制造系统, 2003，9(7):576-581.

FANYushun.ConnotationandKeyTechnologiesofNetworkedManufacturing[J].ComputerIntegratedManufacturingSystems,2003，9(7):576- 581.

[2] 肖倩乔, 李益兵, 左少雄,等. 考虑学习曲线的精益生产制造系统双重资源配置方法[J]. 计算机集成制造系统,2016,22(12):2800-2807.

XIAOQianqiao,LIYibing,ZUOShaoxiong,etal.Dual-resourceConfigurationofManufacturingSystemBasedonLeanProductionConsideringLearningCurve[J].ComputerIntegratedManufacturingSystems,2016,22(12):2800-2807.

[3] 曹岩, 蔺麦田. 基于AHP的制造资源建模与优化选择[J]. 机床与液压, 2009,11(11):224-228.

CAOYan,LINMaitian.ModelingandOptimalSelectionofManufacturingResourcesBasedonAnalyticHierarchyProcess[J].Machinetool&Hydraulics,2009,11(11):224-228.

[4] 王炳刚, 饶运清, 邵新宇, 等．基于多目标遗传算法的混流加工/装配系统排序问题研究[J]．中国机械工程,2009,20(12):1434-1438.

WANGBinggang,RAOYunqing,SHAOXinyu,etal.AMOGA-basedAlgorithmforSequencingaMixed-modelFabrication/AssemblySystem[J].ChinaMechanicalEngineering,2009,20(12):1434-1438.

[5]KOULS,VERMAR.DynamicVendorSelectionBasedonFuzzyAHP[J].InternationalConferenceonSupplyChainManagementandInformation,2010,22(8):1-4.

[6] 包北方, 杨育, 杨涛, 等. 产品定制协同制造资源优化配置[J]. 计算机集成制造系统,2014,20(8):1807-1818.

BAOBeifang,YANGYu,YANGTao,etal.ResourceOptimalAllocationinProductCustomizationCollaborativeManufacturing[J].ComputerIntegratedManufacturingSystems,2014,20(8):1807-1818.

[7] 郏维强, 冯毅雄, 谭建荣, 等. 制造资源混合粒度优化组合方案求解技术[J]. 计算机辅助设计与图形学学报,2012,3(3):281-289.

JIAWeiqiang,FENGYixiong,TANJianrong,etal.SchemeSolvingTechnologyforClusteringOptimizationofManufacturingResourceswithHybridGranularities[J].JournalofComputer-aidedDesignandComputerGraphics,2012,3(3):281-289.

[8] 姜莉莉, 习小英, 李敏, 等. 基于多色集合理论的夹具概念设计研究[J]. 中国机械工程,2006,17(8):832-836.

JIANGLili,XIXiaoying,LIMin,etal.ReseachonConceptualDesignofJigandFixtureBasedonPolychromaticSets[J].ChinaMechanicalEngineering,2006,17(8):832-836.

[9] 潘志毅, 黄翔, 李迎光. 有向图向设计结构矩阵与多色集合同步映射的设计过程规划方法[J]. 计算机集成制造系统,2008,14(7):1274-1280.

PANZhiyi,HUANGXiang,LIYingguang.ProductDesignProcessPlanningMethodBasedonSynchronousMappingFromdirectedGraphtoDesignStructureMatrixandPolychromaticSets[J].ComputerIntegratedManufacturingSystems,2008,14(7):1274-1280.

[10] 吕纪威, 顾寄南. 制造资源配置中的容错处理技术[J]. 机械设计与研究,2010,26(2):82-101.

LYU Jiwei, GU Jinan. Fault-tolerant Processing in Manufacturing Resources Configuration[J]. Machine Design and Research,2010,26(2):82-101.

[11] PAWLAK Z. Rough Sets[J]. International Journal Computer and Information Science,1982(11):314-356.