工程机械用液力变矩器叶片数对其原始特性的影响

武琳琳，惠记庄，2，张泽宇，雷景媛，郑恒玉

0 引言

液力变矩器是车辆自动变速系统中的重要元件，起到传递力矩、转变速度、使系统结合稳定的作用［1］，在工作中叶片受力集中、载荷过大时极易发生疲劳断裂，引发一系列严重后果［2］。通过增加叶片数可分散应力，但叶片数过多会增大液流摩擦面，使有效过流断面变小。因此，研究叶片数对液力变矩器性能的影响是十分必要的。

Sehyun等提出可用导轮叶片开孔的方法来抑制边界层分离，并对导轮叶片不同的开口角度进行分析，证明此方法能大幅提高泵轮的转矩。德国的H Schul等人分析了泵轮和涡轮的不同转速，证明涡轮和泵轮流场之间具有一定关系。北京理工大学的魏巍开发了一套三维优化设计系统，并得到了一组新的叶片参数，通过建立液力变矩器模型并进行优化分析，使得液力变矩器的工作特性得以改善［3-4］。吉林大学的刘春宝提出叶片环量分布类似鱼体结构，并分析了起初叶片的数值，提高了液力变矩器的效率［5］。同济大学的王安麟基于叶片厚度的曲线方程进行模拟分析，结果显示叶片厚度会影响液力变矩器的流场分布［6］。

国内外学者虽然研究了叶片参数对液力变矩器性能的影响，但对叶片数的选取考虑较少。因此，本文通过液力变矩器的三维流场计算分析不同工作轮叶片数对变矩器原始特性的影响，并选取4种叶片数组合方案对计算结果进行验证。

1 液力变矩器的三维流场计算

1.1 原始特性分析

液力变矩器各种性能的变化规律可通过原始特性参数反映［7-8］。原始特性参数包括转速比、变矩系数、传动效率和容量系数等。

(1)转速比 i。

式中:nT为涡轮转速;nB为泵轮转速。

由式(1)可知:转速比i表示输出转速降低的倍数。

(2)变矩系数K。

式中:MT为涡轮转矩;MB为泵轮转矩;MD为导轮转矩。

由式(2)可知:变矩系数K反映输出转矩增大的倍数。

(3)传动效率η。

由式(3)可知，传动效率是变矩系数和转速比的乘积，表征能量从发动机传输到泵轮再传递到涡轮的效率。

(4)容量系数C。容量系数表示液力变矩器吸收外载荷的情况［9-10］。

通过三维流场计算得出各个工作轮流道的转矩，从而得到液力变矩器具体的原始特性参数值。

1.2 三维流场计算

液力变矩器叶片为三维立体结构，其流道内曲率变化复杂，3个工作轮转速不同，故其内流场实质上是非定常的、三维的、不可压缩的黏性流体流动［11-12］。为了准确地描述其内流场流动情况，采用三维流动理论对其进行结构设计。

本文借助Imageware软件对变矩器内部流场进行三维黏性流动计算，数值模拟流场的流程为:建立三维模型、网格划分、选择计算方法和物理模型、设置进出口边界条件、选取材料属性、处理计算结果［13-14］。

1.2.1 液力变矩器流道模型的建立

以某型号液力变矩器为研究对象，其主要参数如表1所示。

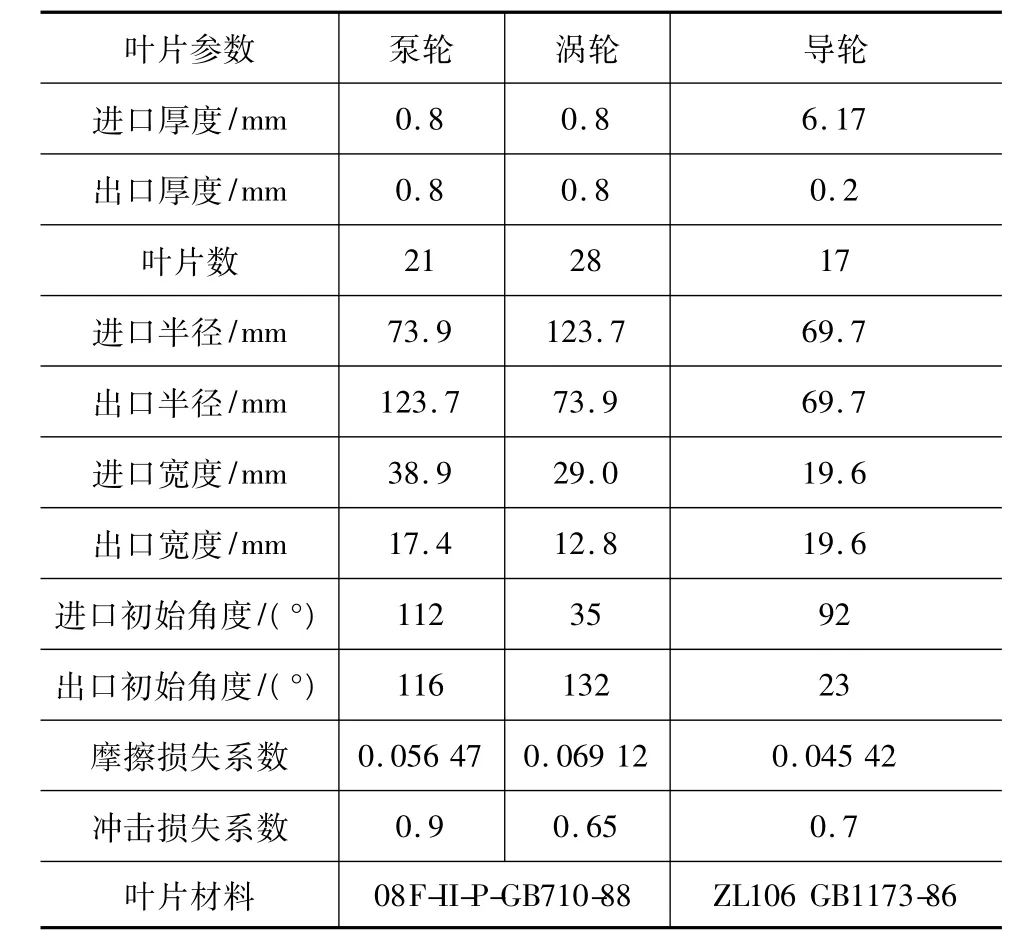
表1 液力变矩器参数

该液力变矩器其余参数为:液力传动油密度ρ=876.6 kg·m原3，泵轮转速 nB=1 700 r·min原1，容量系数 C=0.62，进口流量 Qi=4.32 L·min原1。

利用硅橡胶法提取泵轮流道模型，如图1所示。经过三坐标测量仪扫描后得到泵轮流道的点云数据，在Imageware中对泵轮流道的点云数据进行曲面拟合后得到其点云模型，如图2所示。

将流道的点云模型导入UG软件中，通过对曲面进行裁剪、缝合、实体化等一系列操作，得到流道的三维模型，如图3所示。运用ANSYS对流道模型进行网格划分，得到流道网格模型，如图4所示。

图1 泵轮流道的硅橡胶模型

图2 泵轮流道的点云模型

图3 流道三维模型

1.2.2 计算模型和算法的获取

将流道网格模型导入Imageware软件中，并对湍流模型、耦合算法和离散格式进行设置。

由于标准k-ε模型能够较准确地反映液力变矩器内的流场，并且可对常数值进行调节，减少了对应的法向应变项上所产生的误差。因此，本文分析计算时湍流模型选用标准k-ε模型。

图4 流道网格模型

在Imageware中，PSIO算法对每个迭代过程添加了网格畸变修正和动量修正，一定程度上降低了压力场与动量方程的偏差，减少了获得最终解所需要的迭代次数，使求得收敛解的速度大大加快［15］。因此，本文采用PISO算法以确保快速得到收敛解。另外，本文选取一阶迎风格式为离散格式，以便快速准确地达到理想效果。

1.2.3 流场的数值计算

在流场的计算过程中，为了准确地进行流场数值计算并得到惟一的解，必须在Imageware确定边界条件和初始条件。

本文工作轮进口处压力已知，而速度和流量未知，故将进口面的边界条件设为压力进口边界条件;每个工作轮流道的4个组成面都属于刚性壁面，故将内外环面、压力面和吸力面的边界条件选为WALL壁面条件;上边界条件类型确定之后，采用数据传递方式设置混合面模型。

上述条件设定完成后，给定各个工况下的初始条件，确定收敛准则为残差值减小到三阶量级以下;然后进行三维流场计算，得到各个工况下的数值解。

2 工作轮叶片数对液力变矩器原始特性的影响

在高速比工况下(i=0.71)通过三维流场计算得到各工作轮的转矩，进而绘制变矩器的原始特性曲线，分析叶片数对变矩器性能的影响情况。保持2个工作轮的叶片数不变，根据剩余一个工作轮不同叶片数对应的转矩，得到变矩器的性能参数拟合曲线。

2.1 泵轮叶片数对原始特性的影响

保持涡轮和导轮的叶片数分别为28和17不变，当泵轮叶片数分别为19、21、23时，变矩器的原始特性参数拟合曲线如图5所示。

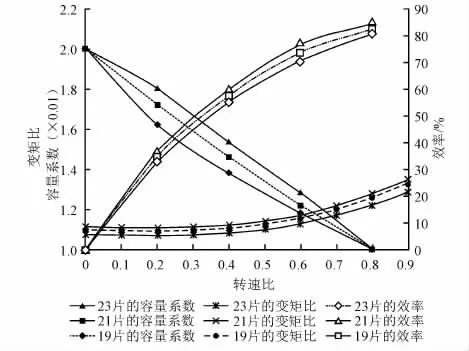
图5 泵轮叶片数对变矩器原始特性的影响

由图5可知:当泵轮叶片数为21时变矩器效率最高，叶片数为19时次之，叶片数为23时效率最低;叶片数分别为21、19、23时对应的变矩比依次减小;容量系数则随着叶片数的增加而逐渐增大，但差异不大。

2.2 涡轮叶片数对原始特性的影响

保持泵轮和导轮的叶片数分别为21和17不变，当涡轮叶片数分别为25、28、31时，变矩器的性能参数拟合曲线如图6所示。

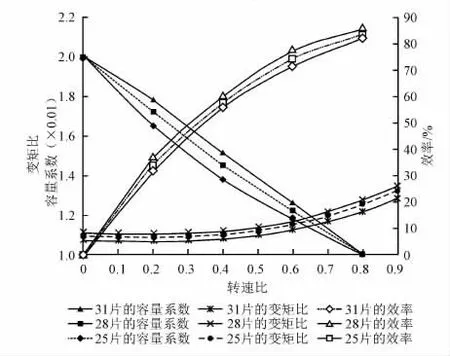
图6 涡轮叶片数对变矩器性能的影响

由图6可知:当涡轮叶片数为28时变矩器效率最高，叶片数为25时次之，叶片数为31时效率最低;叶片数分别为28、25、31时对应的变矩比依次减小;容量系数则随着叶片数增加逐渐增大，但差异不大。

2.3 导轮叶片数对原始特性的影响

保持泵轮和涡轮叶片数分别为21和28不变，当导轮叶片数分别为15、17、19时，变矩器的性能参数拟合曲线如图7所示。

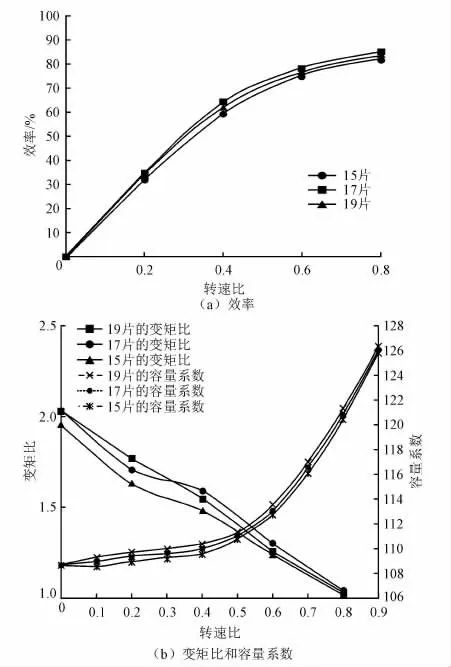
图7 导轮叶片数对变矩器性能的影响

由图7可知:当导轮叶片数为17时变矩器效率最高，叶片数为19时次之，叶片数为15时效率最低;叶片数为19时变矩比最大，但随着转速比的增加呈下降趋势，在转速比接近0.4时变矩比低于叶片数为17时的变矩比，叶片数为15时变矩比最小;容量系数随着叶片数的增加而小幅度增大。

综合液力变矩器各工作轮不同叶片数对其原始特性的影响可知:3个工作轮叶片数变化对变矩器性能的影响相似，叶片数过多或者过少都会降低其效率;当叶片数较少时，随着工作轮叶片数的增加，效率和变矩比都逐渐提高，但叶片数过多时二者反而不断下降;叶片数变化对容量系数的影响较小，随着叶片数的增加容量系数不断升高。

3 叶片数组合与台架试验研究

3.1 组合方案及台架试验

由以上分析可知，叶片数的变化会影响变矩器的原始特性，本节选择几种叶片数组合方案(表2)，利用台架试验对其分析结果进行验证。

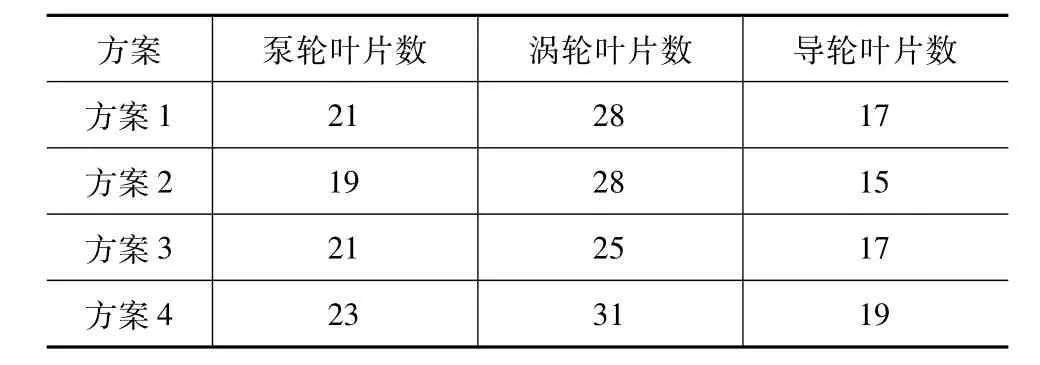
表2 不同叶片数组合方案

由于任一工作轮叶片数改变，液力变矩器都会有所不同，本文的试验结果仅与原始工作轮参数(方案1)进行对比。液力变矩器试验台如图8所示，台架试验原理如图9所示。

图8 液力变矩器试验台

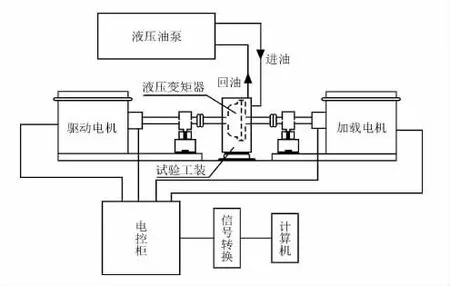
图9 台架试验原理

保持外界环境恒定，改变驱动电机和加载电机的转速，利用转速传感器、扭矩传感器对该液力变矩器进行10组试验，结果如表3所示。

拟合表3的试验结果得到变矩器试验特性曲线。将计算结果仿真特性曲线与试验特性曲线进行对比，如图10所示。

由图10可知，试验与计算的数据较为接近，表明本文基于三维流场的计算结果是准确的，通过三维流场计算液力变矩器性能的方法是可行的。试验与仿真结果的平均误差约为3.1%，最大误差约为4.2%，这是由于建模时对流道进行了简化，忽略了实际过程中热能、噪声能的损失以及结构变形和液体的非定常流动。

表3 变矩器试验结果

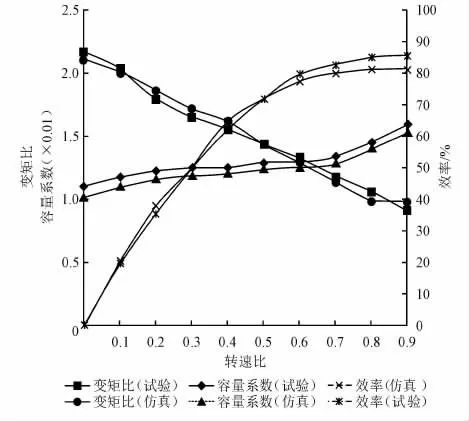
图10 液力变矩器的仿真与试验结果对比

3.2 不同方案对原始特性的影响对比

通过三维流场数值模拟，得到不同方案的变矩器原始特性变化规律，如图11所示。

由图11可知，效率最高的方案1在刚启动时的变矩比最小，而启动时的变矩系数关乎着启动的动力性能，变矩比增大会导致效率下降，反之亦然。容量系数跟仿真结果相比稍有下降，其选择主要考虑与发动机的匹配关系。变矩比一定时，效率增加会降低容量系数，而在保证与发动机匹配的基础上可对其进行小范围的下调。所选4种方案的变矩器效率均达到了80%左右，其中方案1的效率最高，约为86%，方案3的效率次之，其余2种方案的效率则相对较低。

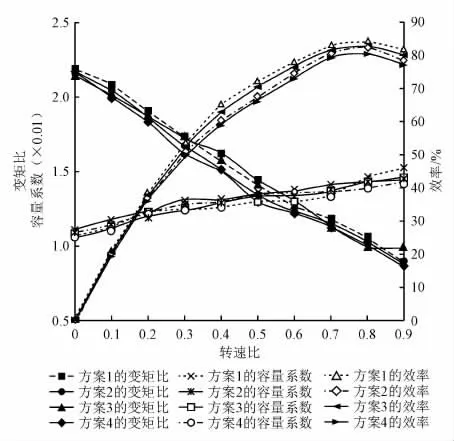
图11 4种方案的变矩器性能对比

4 结语

(1)对液力变矩器的原始特性进行了简要阐述，借助三坐标测量仪得到3个工作轮的流道和整体点云数据，通过Imageware的后处理和UG软件的曲面造型得到了工作轮流道的三维模型。给定各个工况下的初始条件并进行三维流场数值计算，得到各个工况下的数值解。

(2)保持2个工作轮叶片数不变，改变剩余1个工作轮的叶片数，在高速比工况下分别进行三维流场数值计算，并得到不同工作轮叶片数对液力变矩器原始特性的影响:3个工作轮的叶片数变化对变矩器原始特性的影响相似，叶片数过多或者过少都会降低其效率;当叶片数较少时，随着工作轮叶片数的增加，效率和变矩比都逐渐升高，但叶片数过多时二者反而不断下降;叶片数变化对容量系数影响较小，随着叶片数的增加容量系数不断升高。

(3)根据工作轮叶片数的不同组合了4种方案。对方案1所组合的液力变矩器性能进行了台架试验，将试验结果拟合得到其原始特性曲线，试验结果与仿真数据的平均误差约为3.1%，最大误差约为4.2%。通过对比4种方案分别拟合得到的原始特性曲线，验证了本文三维流场的计算结果是准确的，三维流场计算液力变矩器原始特性的方法是可行的。

(4)本文是在稳态状况下分析不同叶片数对变矩器原始特性的影响，而变矩器内流场是非稳态的，并且由于变矩器内部结构的复杂性和叶片结构的扭曲性，一个参数的变化会影响到叶型的其他参数，本文未对各种参数进行综合考虑，今后需要进一步研究。

参考文献:

［1］ 许 涛，过学迅.FLUENT在汽车工业中的应用［J］.北京汽车，2006(5):39-41.

［2］ 惠记庄，曹 杰，邹亚科，等.钣金型液力变矩器疲劳寿命模拟仿真与实验研究［J］.机械设计，2011，28(6):74-78.

［3］ 魏 巍，闫清东，朱 颜.液力变矩器叶片流固耦合强度分析［J］.兵工学报，2008，29(10):1158-1162.

［4］ 魏 巍，闫清东.液力变矩器叶栅系统三维优化设计方法研究［J］.气体传动与控制，2006，17(4):41-44

［5］ 刘春宝，刘长锁，马文星，等.基于鱼体结构的仿生型液力变矩器叶片环量分配规律［J］.北京理工大学学报:自然科学版，2016，36(9):887-892，904

［6］ 王安麟，刘伟国，龙广成.基于液力变矩器流体耦合叶片厚度设计方法［J］.同济大学学报，2015，43(4):599-604

［7］ 惠记庄.基于三维流场的钣金型液力变矩器现代设计方法与实验研究［D］.西安:长安大学，2010

［8］ 惠记庄，张广辉，聂春鹏，等.钣金型液力变矩器外特性计算方法［J］.交通运输工程学报，2015，15(1):74-81.

［9］ WHITFIELD A，WALLACE F J， PATEL A.Performance Prediction of Multi Element Torque Converters［J］.International Journal of Mechanical Sciences，1983，25(2):77-85.

［10］ 许 涛.液力变矩器三维流场仿真计算［D］.武汉:武汉理工大学，2006.

［11］ 惠记庄，胡 浩，代 然，等.基于MSC的变矩器膨胀变形分析［J］.中国公路学报，2015，28(5):144-149.

［12］ 麦云飞，刘磊然，郭 瑞.基于Fluent软件的SCR摆线转子泵控制方程模型及算法探究［J］.通信电源技术，2015，32(6):95-98.

［13］ 惠记庄，张金龙，雷景媛，等.装载机闭锁式液力变矩器的闭锁控制及仿真分析［J］.筑路机械与施工机械化，2017，34(3):95-102.

［14］ RONALD DFLACK，LEONARD DWHITEHEAD.Velocity Measurements in an Automotive Torque Converter PartⅡ-Average Turbine and Stator Measurements［J］.Tribology Transactions.1999，42:697-706.

［15］ 惠记庄，郑恒玉，杨永奎，等.基于三维流场数值解的钣金型液力变矩器轴向力计算［J］.中国公路学报，2016，29(4):145-152.