γ-TiAl单晶塑性变形中晶粒转动的CPFEM模拟

赵文娟，张 露，李晓滨，彭远祎，黄明丽，林启权



-TiAl单晶塑性变形中晶粒转动的CPFEM模拟

赵文娟1, 2，张 露1, 2，李晓滨3，彭远祎1, 2，黄明丽4，林启权1, 2

(1. 湘潭大学 机械工程学院，湘潭 411105；2. 湘潭大学 焊接机器人及应用技术湖南省重点实验室，湘潭 411105；3. 中冶建筑研究总院有限公司，北京 100088；4. 东北大学 秦皇岛分校，秦皇岛 066004)

-TiAl合金；晶体塑性；取向；晶粒转动；塑性变形；有限元

在航天、航空、船舶及汽车等领域有广阔应用前景的轻质金属结构材料中，TiAl基合金以其低密度、高比强度、高比模量、良好的阻燃能力、抗氧化性及抗蠕变性能等倍受青睐[1−4]。目前，通过实验、计算模拟等手段对TiAl基金属间化合物的力学性能研究方兴未艾，晶体塑性有限元方法(Crystal plasticity finite element method，CPFEM)是其中的一种有效研究手段，持续吸引着研究者们的目光。

近年来，TiAl合金力学行为的相关数值计算已取得一定的研究进展。KAD等[5]首次利用晶体塑性理论模拟二维全片层-TiAl组织，认为片层的变形方式仅有软剪切和硬剪切两种模式，这样的过度简化使得其模拟结果与试验结果之间存在较大的偏差。ZAMBALDL等[6]通过建立简单的三维几何模型，研究层片状-TiAl基合金的塑性各向异性行为，发现晶粒取向影响着-TiAl基合金的塑性变形性能；且不同取向晶粒的屈服强度存在较大差异，与实验结果基本吻合。FALLAHI等[7]运用晶体塑性有限元方法，模拟了-TiAl双晶、三晶拉伸过程中不同晶粒取向对应力集中的影响，发现在应力集中的横截面上形成较大的应力梯度，有颈缩转动的趋势。另一方面，陈守东等[8]在铜极薄带轧制中滑移与变形的晶体塑性有限元模拟中，发现晶粒间及晶粒内的转动均会引起材料内部变形的不均匀。邓运来等[9]在对高纯铝柱状晶的冷轧试验研究中发现，形变晶粒各部分具有不同的转动趋势，靠近晶界部分的转动角度较小。AKHTAR[10]在单晶纯钛的拉伸试验中，发现随着剪切应变的增大，晶格转动使柱面滑移系得以启动。由此，在TiAl基合金的塑性变形中，明晰晶粒转动现象的成因，探索取向对晶粒转动及合金塑性变形行为的影响作用将对深入理解其微观塑性机制有着重要的意义。

-TiAl基合金主要由-TiAl和Ti3Al相组成，其中Ti3Al相变形困难，变形主要发生在-TiAl相内。由于-TiAl合金片层组织中L10结构的相的á110]和á011]取向在晶体学上不等价，导致这种复杂的晶体取向关系对-TiAl合金塑性变形中滑移系的启动和滑移有着重要的影响。-TiAl相中主要存在的滑移系有： 4个普通滑移系á110]{111}，8个超滑移系á011]{111}和4个孪生系á112]{111}[11−14]。本研究基于以上的-TiAl主要滑移系选取晶粒的初始取向，建立综合考虑普通位错、超位错和孪生的晶体塑性有限元本构关系模型。模拟不同取向条件下-TiAl单晶的拉伸变形，观察变形中剪切应变的变化，研究拉伸中晶粒转动与晶粒初始取向之间的相互作用关系。

1 晶体塑性理论

1.1 晶体剪切滑移理论

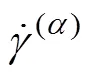
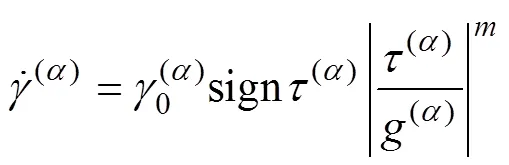
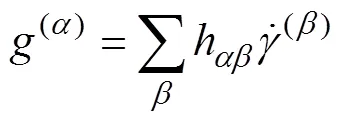
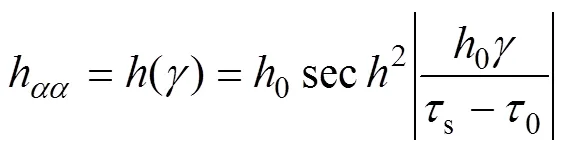
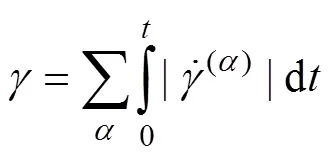
1.2 晶粒转动的表征方法

晶体变形除了滑移和孪生外，晶粒的转动对晶体的变形有着不可忽视的作用。本研究在拉伸模拟过程中，着重关注垂直于拉伸轴的平面(平面)上的晶粒转动情况，通过晶粒的剪切应变来定量判断晶粒转动角度的大小。

物体变形前后其线元将发生转动，转动角度的大小可用线元来表示[16]。假设变形前两个任意线元的单位矢量分别为和，方向余弦分别为v和t，则夹角余弦为：

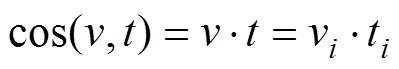
利用格林应变张量，式(5)可转化为：

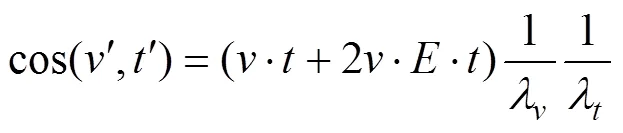
由式(6)可以求得线元变形前后的夹角变化。又知变形前两线元相互垂直，则=0，于是上式可以化 简为

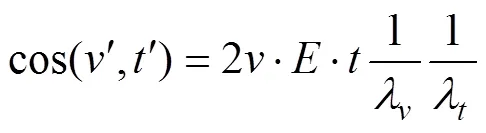
在小变形情况下，忽略二阶小量，并令为变形后线元间直角的减小量，则由式(7)可得：

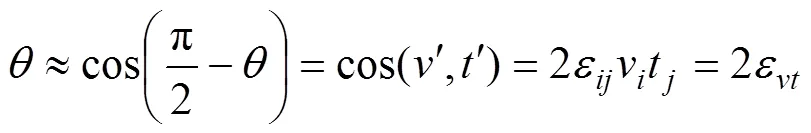
从式(8)可以看出，晶粒转动角度的大小是应变分量大小的2倍。

2 模拟过程

2.1 模型建立

本研究基于ABAQUS平台，利用黄永刚[17]的UMAT编写适合-TiAl合金的晶体塑性本构子程序，建立-TiAl单晶的晶体塑性有限元模型。模拟晶胞尺寸为0.5 mm×0.5 mm×1 mm，包含250个单元，单元类型为C3D8，如图1所示。拉伸中，将模型中的一个端面固定，另一端面施加沿Z轴的拉伸载荷，变形速率为0.01 mm/s，拉伸至工程应变为0.1。

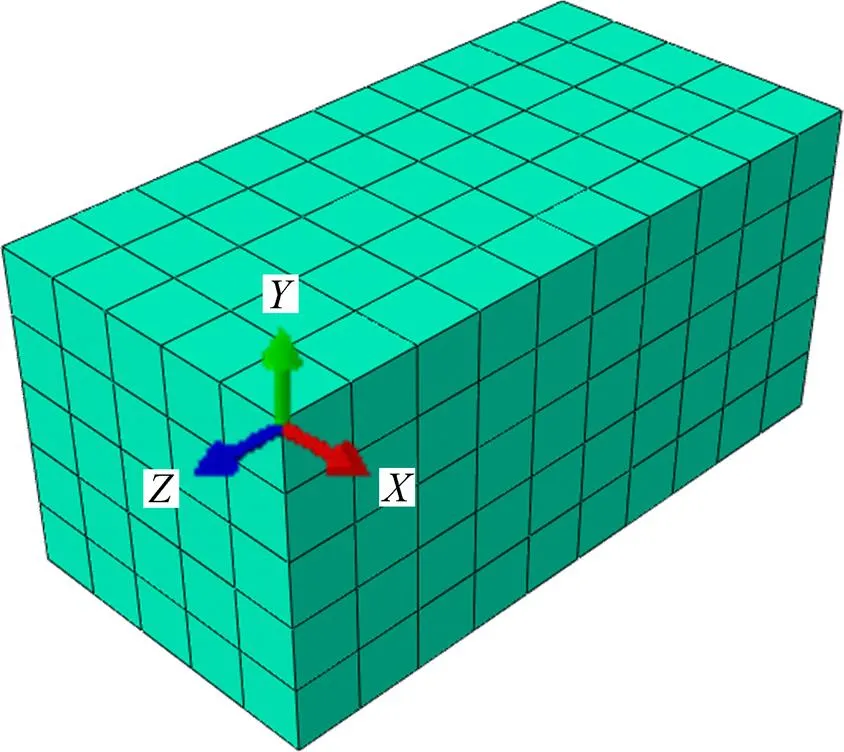
图1 单晶体模型示意图

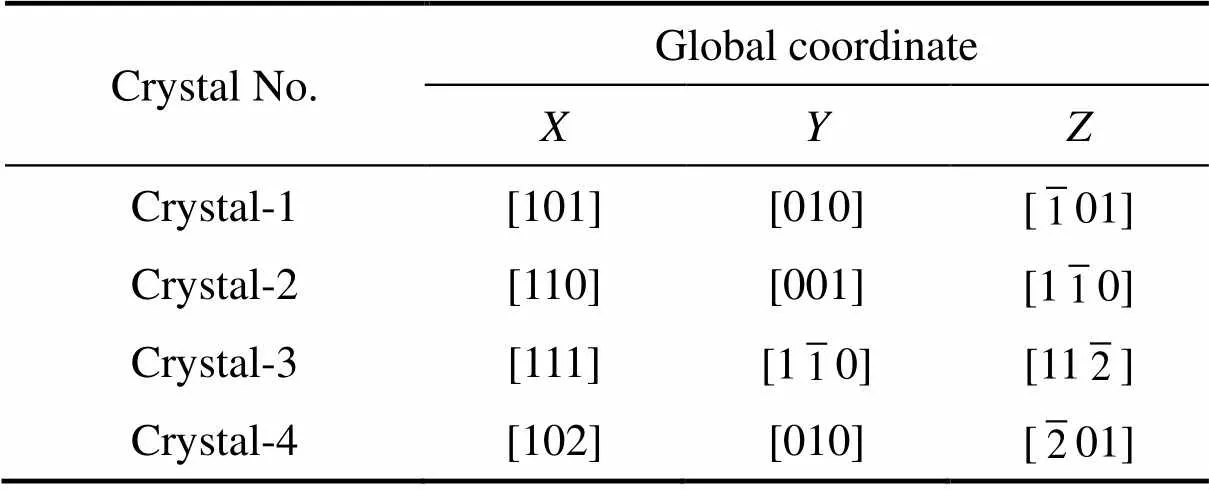
表1 局部坐标与整体坐标系的关系

2.2 参数设定

室温下-TiAl的单晶体弹性模量参数[11−13]如表2所示。参考AKHTAR等[10−12]的实验研究，选取适合-TiAl单晶材料本身的参数。-TiAl的主要滑移系可分为普通滑移系、超滑移系和孪生系，如表3所示。普通滑移系的临界剪切应力取130 MPa，孪生系的临界剪切应力值与之相同，超滑移系的临界剪切应力取200 MPa。单晶第一阶段饱和流动应力s取初始临界剪切应力的1.3倍。普通滑移系、超滑移系和孪生系的初始硬化模量分别取400、500和400 MPa。

表2 γ-TiAl单晶体的弹性模量[11−13]

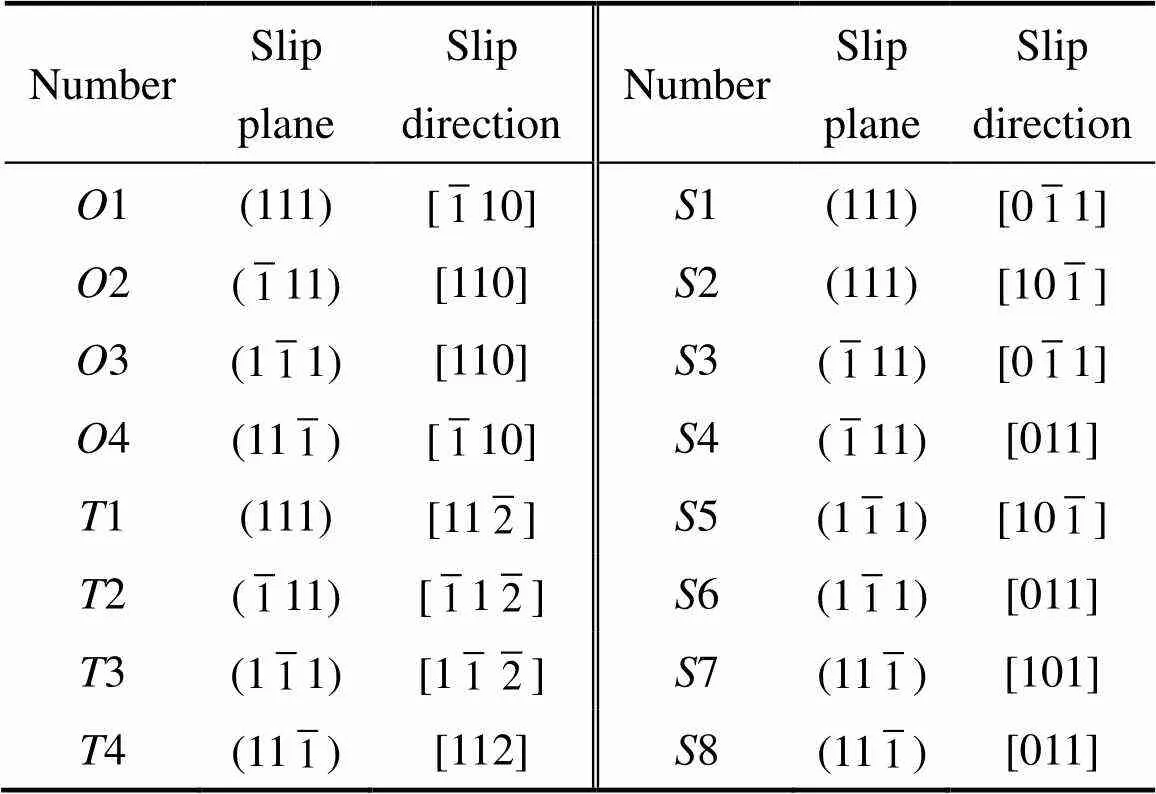
表3 γ-TiAl的滑移系

3 结果与讨论

晶粒1~4拉伸变形终了时剪切应变的三维分布图如图2(a)~(d)所示。图3(a)~(d)分别显示了晶粒1~4拉伸变形终了时垂直于拉伸方向(轴)的截面上最大剪切应变的分布情况。拉伸变形的剪切应变观察结果表明，晶粒1~4的剪切应变是由中心部位到边缘逐渐增大的。晶粒中的剪切应变主要集中在晶粒的边缘位置，并且在晶界处有最大值；而在晶粒的中心部位几乎没有剪切应变。图2(a)所示为晶粒1拉伸变形终了时的剪切应变示意图，沿轴方向上的应变分布出现正负交替的现象。同时，由图3(a)可见晶粒1的截面上剪切应变呈对称分布，其平面绕轴发生旋转，两者的共同作用导致晶粒发生扭转。与晶粒1类似，其他晶粒也发生了不同程度的晶粒转动。晶体在塑性变形过程中发生扭转，已在一些实验观察中得到证实。AKHTAR[10]对纯钛的拉伸试验中，发现滑移是发生塑性变形的主要原因，同时滑移引起晶格转动。黄文等[18]通过模拟计算的方法，建立与Akhtar实验类似的纯钛拉伸模型，其结果与实验结果基本一致。图4中显示了模拟中变形前后的有限元网格模型，从图4(b)可以看出晶粒发生明显的扭转。该研究认为在不同剪切应变时，不同滑移系的启动和作用，导致晶格的转动。本研究中，图5所示为晶粒1~4在拉伸中滑移系发生的累计剪切应变，、、分别代表普通滑移系、孪生滑移系和超滑移系(如表3所示)的累计应变。从图5(a)中可以看出，晶粒1变形中主要依靠普通滑移发生剪切变形，其他两种变形方式基本无贡献，晶粒4与之类似。晶粒2中以超滑移系的变形为主，而晶粒3中的3种变形方式对变形都表现出一定的贡献，唯有孪生系贡献较小。由此，晶体沿不同的取向拉伸，其滑移系的启动情况不尽相同。其中，普通滑移系容易启动，进而发生剪切变形；而孪生系与超滑移系对变形的贡献较小。晶体变形的本质是滑移系发生剪切应变，本研究的模拟结果表明，在拉伸应力的作用下，-TiAl单晶晶粒发生了不同程度的扭转，这与相关实验现象、模拟计算结果基本一致。

拉伸变形终了时的三维应力分布如图6所示，可以看出应力分布的不均匀，由于晶粒的畸变导致形成较大的应力梯度。结合图2可以发现，应力梯度较大的区域对应的应变也相应较大。同时，如图7所示，从垂直于拉伸轴的截面应力分布中也可以看出，应力的分布基本是边缘区域的应力集中显著，而中心区域应力梯度比较小，即在晶粒边界变形程度较大，中心区域无明显变形。结合剪切应变的分布规律可知，在拉伸变形过程中，晶粒的转动是垂直拉伸轴(轴)的截面(截面)发生明显的扭转，且转动的幅度由中心到边界逐渐增大。

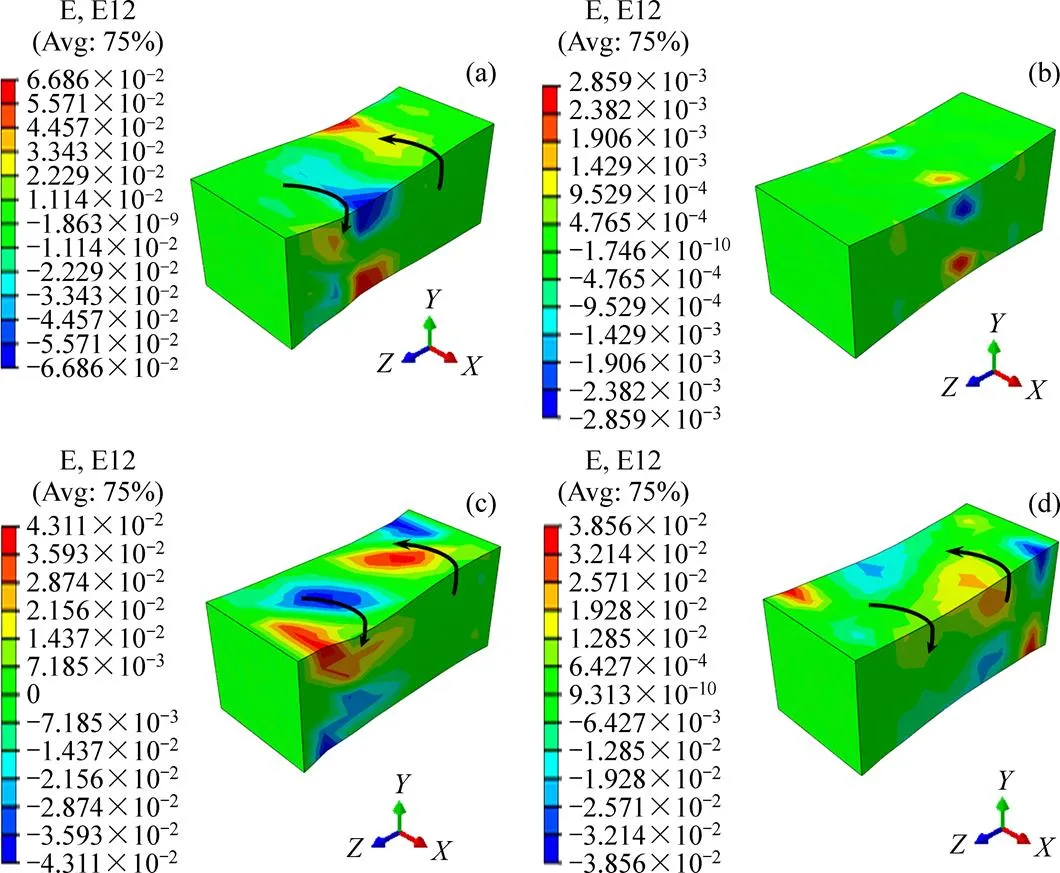
图2 拉伸变形终了时不同取向晶粒的剪切应变分布

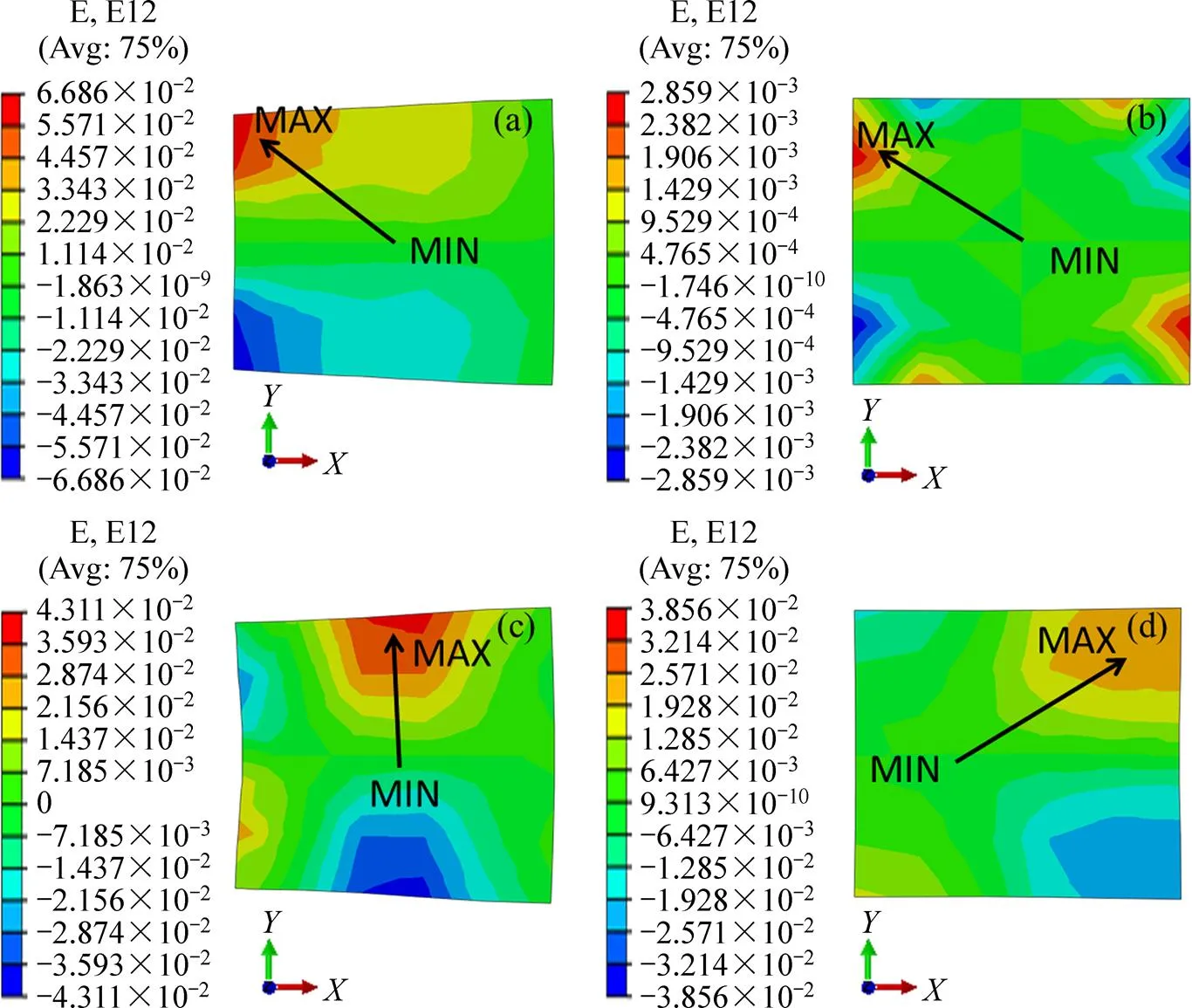
图3 垂直于拉伸轴XY截面剪切应变分布示意图

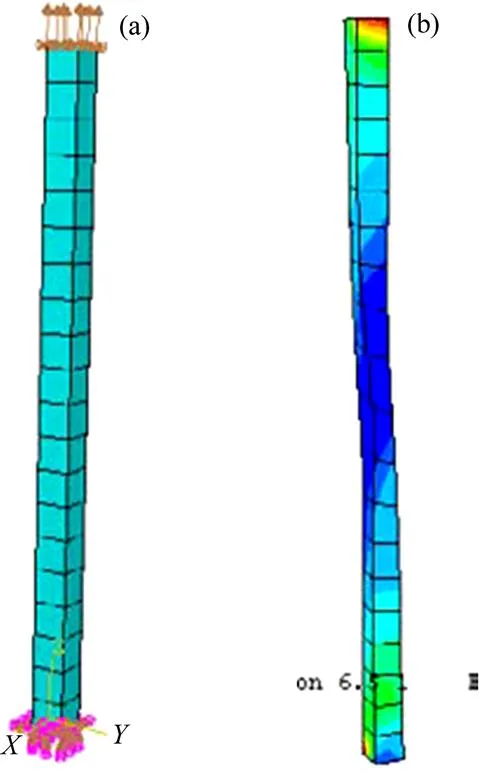
图4 变形前和变形后钛单晶有限元模型[17]

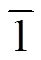
图5 不同拉伸取向下滑移系的剪切应变

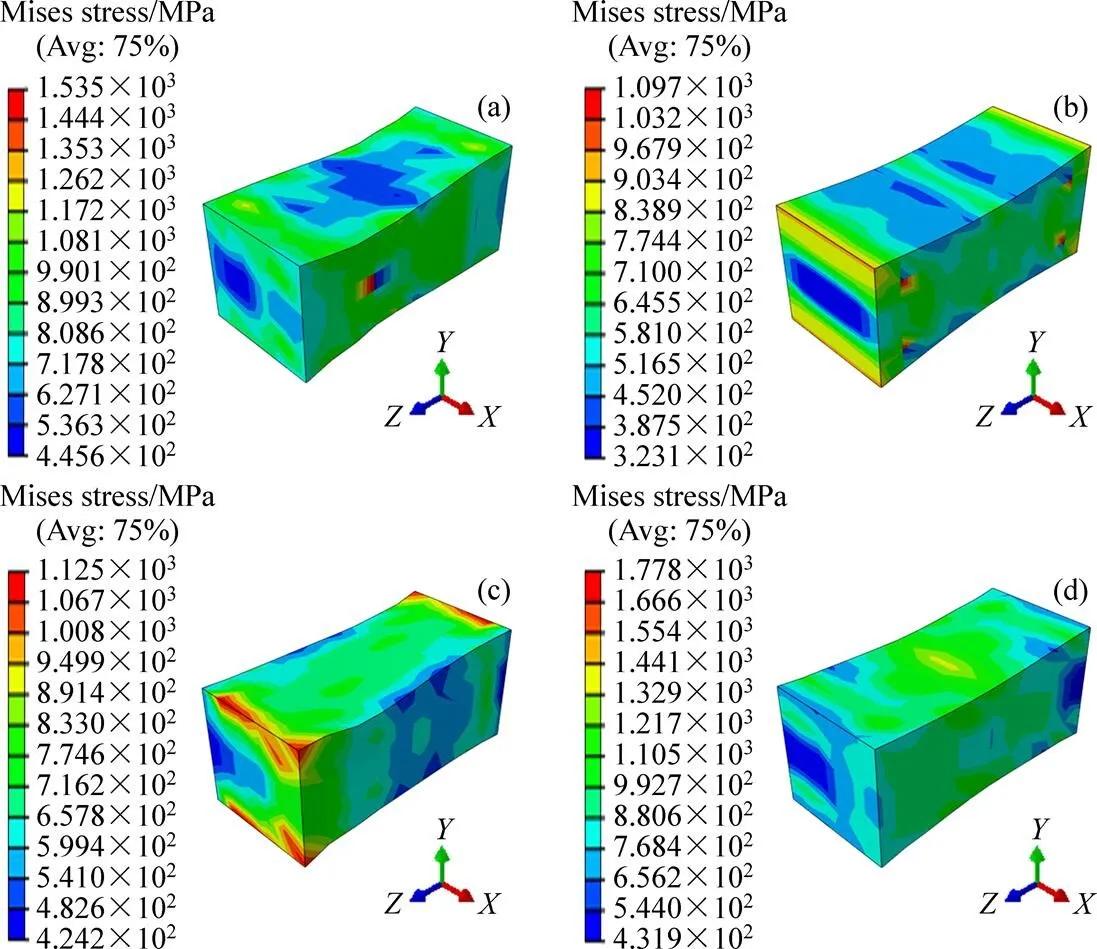
图6 拉伸变形终了时不同取向晶粒的应力分布

图7 垂直于拉伸轴XY截面的应力分布示意图

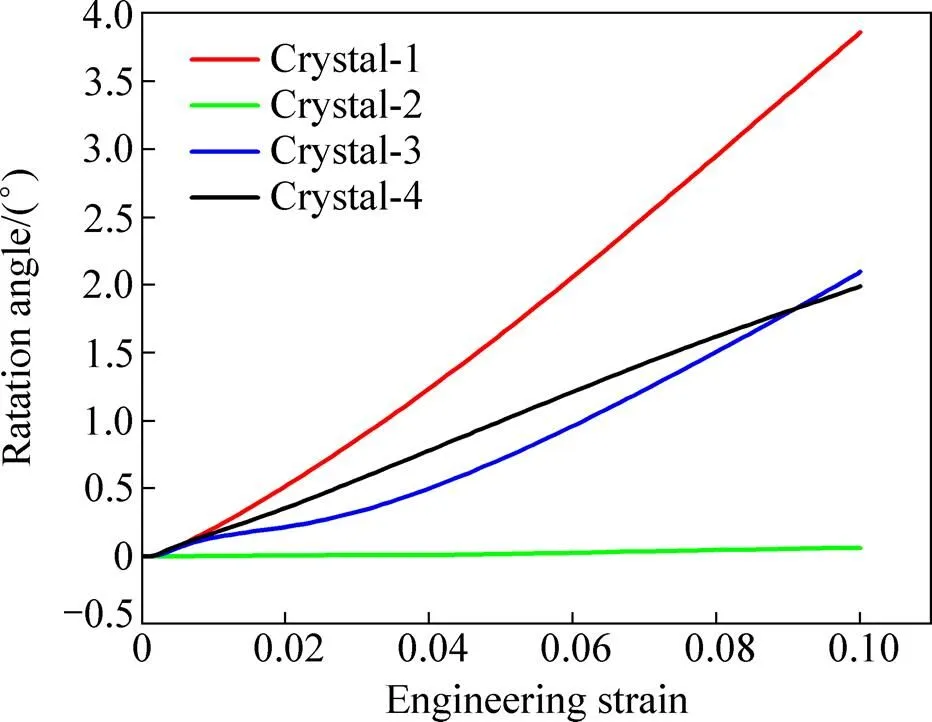
图8 旋转角度随工程应变变化曲线

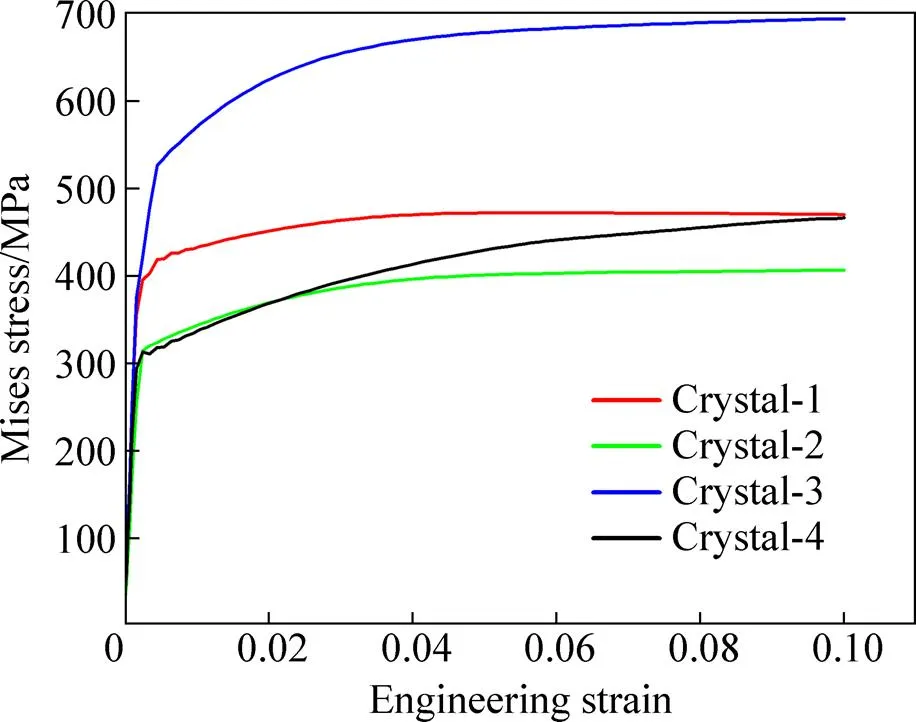
图9 等效应力随工程应变变化曲线

4 结论

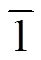
2) 拉伸变形中，晶粒内的剪切应变由中心到边界逐渐增大，剪切应变的最大值出现在边界处，表明晶粒在塑性变形中以心部为中心发生显著的转动。该结果与实验现象相吻合，表明本数值模型可较为准确地描述-TiAl单晶塑性变形中的晶粒转动现象。

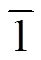
4) 拉伸取向不同时，各滑移系对变形的贡献不同，滑移系的启动与晶粒取向关系密切。其中普通滑移系对变形的贡献最大，孪生系和超滑移系对变形的影响较小。

[1] YANG He, WU Chuan, LI Hong-wei, FAN Xiao-guang, ZHANG Da-wei, JI Zhe. Review on development of key technologies in plastic forming of titanium alloy[J]. Materials China, 2011, 30(6): 6−13.

[2] LI Cui, LI Bin, WU Ze-feng, QI Xiao-yong, YE Bing, WANG Ai-hua. Stitch welding of Ti-6Al-4V titanium alloy by fiber laser[J]. Transactions of Nonferrous Metals Society of China, 2017, 27(1): 91−101.

[3] FOJT J, JOSKA L, MÁLEK J. Corrosion behaviour of porous Ti-39Nb alloy for biomedical applications[J]. Corrosion Science, 2013, 71(3): 78−83.

[4] 罗媛媛, 毛小南, 奚正平, 杨英丽, 吴金平, 苏航标.新型-TiAl基合金在高温变形过程中的组织演变[J]. 中国有色金属学报, 2014, 24(2): 403−408.

LUO Yuan-yuan, MAO Xiao-nan, XI Zhen-ping, YANG Ying-li, WU Jin-ping, SU Hang-biao.Microstructure evolution of new-TiAl alloy during hot deformation[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(2): 403−408.

[5] KAD B K, DAO M, ROBERT J A. Numerical simulations of stress-strain behavior in two-phase2+lamellar TiAl alloys[J]. Materials Science and Engineering A, 1995, 192/193: 97−103.

[6] ZAMBALDI C, ROTERS F, RAABE D. Analysis of the plastic anisotropy and pre-yielding of (/2)-phase titanium aluminide microstructures by crystal plasticity simulation[J]. Intermetallics, 2011,19: 820−827.

[7] FALLAHI A, ATAEE A. Effects of crystal orientation on stress distribution near the triple junction in a tricrystal-TiAl[J]. Materials Science and Engineering A, 2010, 527: 4576−4580.

[8] 陈守东, 刘相华, 刘立忠, 宋 孟. Cu极薄带轧制中滑移与变形的晶体塑性有限元模拟[J]. 金属学报, 2016, 52(1): 120−128.

CHEN Shou-dong, LIU Xiang-hua, LIU Li-zhong, SONG Meng. Crystal plasticity finite element simulation of slip and deformation in ultrathin copper strip rolling[J]. Acta Metallurgica Sinica, 2016, 52(1): 120−128.

[9] 邓运来, 张新明, 刘 瑛, 唐建国, 周卓平. 冷轧高纯铝柱状晶粒的组织与微取向的不均匀性[J]. 中国有色金属学报, 2005, 15(8): 1173−1178.

DENG Yun-lai, ZHANG Xin-ming, LIU Ying, TANG Jian-guo, ZHOU Zhuo-ping. Inhomogeneities of microstructures and micro-orientations in cold-rolled high purity Al columnar grains[J].The Chinese Journal of Nonferrous Metals, 2005, 15(8): 1173−1178.

[10] AKHTAR A. Basal slip and twinning in-titanium single crystals[J]. Metallurgical Transactions A, 1975, 6: 1105−1113.

[11] MARKETZ W T, FISCHER F D, CLEMENS H. Deformation mechanisms in TiAl intermetallics—Experiments and modeling[J]. International Journal of Plasticity, 2003, 19: 281−321.

[12] APPEL F, WAGNER R. Microstructure and deformation of two-phase-titanium aluminides[J]. Materials Science and Engineering, 1998, R22: 187−268.

[13] SCHLOGL S M, FISCHER F D. Micromechanical modelling of TiAl intermetallics[J]. Computational Materials Science, 1996,7: 34−39.

[14] 徐东生, 王 皞, 杨 锐, SACHDEV A K. 钛铝中á011]超位错的非对称形核及运动的分子动力学模拟[J]. 科学通报, 2013, 58(35): 3722−3732.

XU Dong-sheng, WANG Hao, YANG Rui, SACHDEV A K. MD simulation of asymmetric nucleation and motion ofá011] superdislocations in TiAl[J]. Chinese Science Bulletin, 2013, 58(35): 3722−3732.

[15] ASARO R J, NEEDLEMAN A. Texture development and strain hardening in rate dependent polycrystals[J]. Acta Metall, 1985, 33(6): 923−953.

[16] 周益春. 材料固体力学(上册) [M]. 北京: 科学出版社, 2005: 55−63.

ZHOU Yi-chun. Solid mechanics in materials (I)[M]. Beijing: Science Press, 2005: 55−63.

[17] HUANG Yong-gang. A user-subroutine incorporation single crystal plasticity in the ABAQUS finite element program[D]. Cambridge, MA: Harvard University, 1991.

[18] 黄 文, 汪 洋, 葛 鹏, 黄中伟. 单晶纯钛的细观力学性能模拟[J]. 稀有金属材料与工程, 2010, 39(3): 469−472.

HUANG Wen, WANG Yang, GE Peng, HUANG Zhong-wei. Meso-scale simulation on mechanical behavior of single crystal titanium[J]. Rare Metal Materials and Engineering, 2010, 39(3): 469−472.

[19] 郑为为, 杨王玥, 孙祖庆. B2结构Fe3Al单晶在室温拉伸过程中的取向转动[J]. 金属学报, 2000, 36(11): 1161−1164.

ZHENG Wei-wei, YANG Wang-yue, SUN Zu-qing. The rotation of the B2 ordered Fe3Al single crystal during room temperature tensile[J]. Acta Metallurgica Sinica, 2000, 36(11): 1161−1164.

[20] EDWARDS T E J, GIOACCHINO F D, ROCÍO M, CLEGG W J. Deformation of lamellar TiAl alloys by longitudinal twinning[J]. Scripta Materialia, 2016, 118: 46−50.

[21] GIOACCHINO F D, CLEGG W J. Mapping deformation in small-scale testing[J]. Acta Materialia, 2014, 78: 103−113.

(编辑 何学锋)

CPFEM simulations on grain rotation of-TiAl single crystal during plastic deformation

ZHAO Wen-juan1, 2, ZHANG Lu1, 2, LI Xiao-bin3, PENG Yuan-yi1, 2, HUANG Ming-li4, LIN Qi-quan1, 2

(1.School of Mechanical Engineering, Xiangtan University, Xiangtan 411105, China;2. Key Laboratory of Welding Robot and Application Technology of Hunan Province,Xiangtan University, Xiangtan 411105, China;3. Building and Construct Research Institute Co. Ltd. of MCC, Beijing 100088, China;

4.Northeastern University at Qinhuangdao, Qinhuangdao 066004, China)

-TiAl alloy; crystal plastic; orientation; grain rotation; plastic deformation; finite element

Projects(51201147, 51301032) supported by the National Natural Science Foundation of China; Project(14JJ6016) supported by the Natural Science Foundation of Hunan Province, China

2017-01-03;

2017-07-21

ZHAO Wen-juan; Tel: 13787031201; E-mail: wjzhao1024@xtu.edu.cn

10.19476/j.ysxb.1004.0609.2018.03.04

国家自然科学基金资助项目(51201147，51301032)；湖南省自然科学基金资助项目(14JJ6016)

2017-01-03；

2017-07-21

赵文娟，副教授，博士；电话：13787031201；E-mail：wjzhao1024@xtu.edu.cn

1004-0609(2018)-03-0465-09

TG146.2

A