双星探测多目标跟踪改进算法研究
罗招贤, 邵 雷, 虞文鹏
(1.江西经济管理干部学院,南昌 330088; 2.西安卫星测控中心,西安 710043)
0 引言
利用天基预警卫星跟踪空间目标[1-6]的研究有很多,大致可以分为两类:一类是基于弹道模板的跟踪,在跟踪前就已经获取弹道导弹的先验信息,凭借单颗卫星就能实现对弹道目标的跟踪;另一类是基于运动学的跟踪,在无先验信息的条件下,根据弹道目标的运动特性建立符合该特性的运动方程,并通过观测值实
时更新目标状态。基于弹道模板的方法需要庞大的弹道导弹数据库以及较为精准的匹配算法作为支撑,而弹道导弹作为战略层次的武器,向来是各国重点保护对象,想要获取一个较为完备的弹道导弹数据库极其困难,在现实中不具备可操作性,因此本文采用基于运动学的跟踪方法。
由于卫星采取无源探测方式,只能得到目标的角度信息,而无法获得距离信息,可观测性较弱,基于运动学的跟踪方法需要双星协同探测才能确定目标的三维空间位置。在双星协同探测对多目标跟踪[7-10]的过程中,目标航迹交叉会对跟踪产生较大的影响,使得跟踪发生异常现象。针对此问题,本文提出基于二元多项式思想的量测方程构造方法设计了BPGM-SME算法。在滤波算法方面,传统的非线性滤波算法[11-12]包括无迹卡尔曼滤波(UKF)算法[13-16]和粒子滤波(PF)算法[17],PF算法的缺点在于运算时间较长,无法满足预警卫星的实时性要求,UKF算法的运算实时性较好,但是由于预警卫星的观测性较弱,存在跟踪精度低和收敛性差的问题,针对此问题,本文提出了基于迭代思想的UKF算法。
1 双星可观测性分析
天基红外预警系统采用无源探测,至少同时需要两颗卫星才能求解目标的三维空间位置。双星观测几何如图1所示。
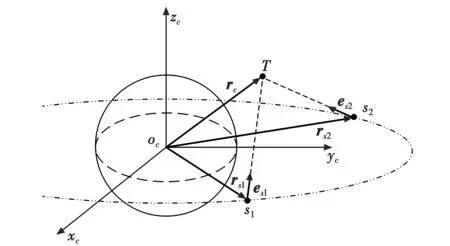
图1 双星观测几何Fig.1 Double satellite observation geometry
假设地心直角坐标系中卫星s1,s2的位置分别为rs1=(xs1,ys1,zs1)T和rs2=(xs2,ys2,zs2)T,设目标T在地心直角坐标系中的位置为rc=(xc,yc,zc)T。列写直线对称式方程为
(1)
其中,es1=(ex1,ey1,ez1)T和es2=(ex2,ey2,ez2)T分别为卫星对目标的单位视线向量。
将式(1)整理成矩阵形式,有
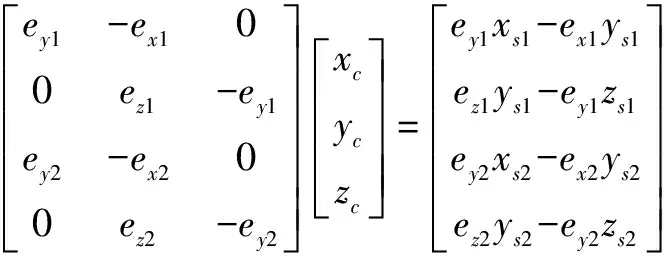
(2)
可简写为
F4×3rc,3×1=b3×1。
(3)
由式(3)可知,用4个方程求解3个参数,利用双星可对目标三维空间定位。
2 状态方程及观测方程
2.1 状态方程
本文在弹道导弹主动段模型中采用重力转弯模型近似导弹运动。假设在地心直角坐标系中,导弹的位置矢量为rc,速度矢量为vc,建立运动方程,有
(4)
式中:‖·‖为矢量长度;αt为推力与空气阻力合力产生的加速度;μ为地球引力常数。
建立重力转弯运动模型,有
(5)
式中,βt为相对质量损耗率。
对于主动段的弹道导弹,有状态方程
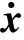
(6)
式中:x=[x,y,z,vx,vy,vz,αt,βt]T为状态向量,x,y,z分别表示地心直角坐标系中目标的坐标位置,vx,vy,vz为目标速度在地心直角坐标系各轴上的坐标分量,αt为轴向加速度;函数f[·]表示目标所采用的运动模型;w(t)表示建模的补偿误差。
2.2 观测方程
设u1,v1为目标在某颗卫星像平面坐标上的坐标,则有观测向量z1=[u1,v1]T为
(7)
式中:h为常系数;ψ1为观测角;ε1为方向夹角;g为重力加速度;a1为加速度;rc,rs1为观测位置矢量。
u2,v2为目标在另一颗卫星像平面坐标上的坐标,则有观测向量z2=[u2,v2]T为
(8)
z=[u1,v1,u2,v2]T为观测向量,有
z(t)=h1[x(t)]+v(t)
(9)
式中:h1[·]为映射函数;v(t)是观测误差。
3 算法设计
3.1 基于二元多项式思想的SME
3.1.1新量测方程
SME是基于多项式的思想得到的,以一维空间Kamen乘积和形式SME为例,新量测方程为
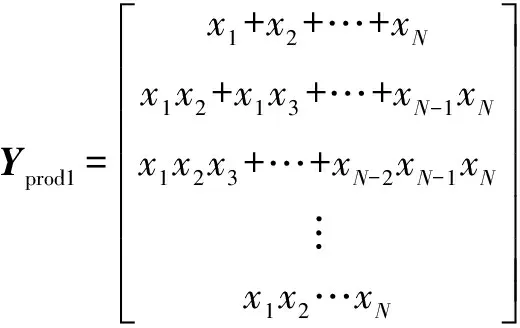
(10)
式中,xi为第i(i=1,2,…,N)个目标的位置在x轴上的坐标值,i=1,…,N。
构造因式pi=s+xi得量测方程,有
(11)
式中,ai集合为Kamen乘积和形式SME即多项式系数。
进一步将SME方法推广到二维空间,以二维Kamen乘积和形式SME为例,有
(12)
式中,xi,yi(i=1,2,…,N)分别是第i个目标的位置在x轴、y轴上的坐标值。
在二维空间中,同时跟踪两个目标,对两个目标的量测量为z1=[x1,y1]T,z2=[x2,y2]T,有Kamen乘积和形式SME,为
(13)
为进一步消除量测过程中的“鬼点”,提出基于多项式分解的改进方法。构造因式
qi=s+txi+yi
(14)
式中,xi,yi分别表示第i个目标的位置在x轴、y轴上的坐标值。有多项式
(15)
新量测集即为多项式系数bij所组成的集合,当N=2时,新量测可以表示为
(16)
当新量测集已知时,得到x轴和y轴的观测集分别为{x1,x2}和{y1,y2}。假定此时,依然存在“鬼点”,则有
(17)
式(17)表明,当x1=x2或y1=y2时,会发生坐标间不明确关系。一旦x1=x2或y1=y2,集合{(x1,y1),(x2,y2)}与{(x1,y2),(x2,y1)}并没有区别。由此可见,算法在改进后,“鬼点”现象得到有效抑制。
3.1.2观测误差协方差阵
假设在一维空间含误差的原始量测值为
zi=xi+ui
(18)
式中:xi为真实值;ui为观测误差。
经过hi对称变换后的新量测误差vi展开如下
vi=hi[(z1(k),z2(k),…,zN(k))-hi(x1(k),x2(k),…,xN(k))]=
(19)
设在新量测方程中,观测误差向量为V=[v1,…,vn]T,n为新量测方程个数,新观测误差协方差阵可以通过R=E[VVT]求得。
定理1假设u=[u1,…,um]T~N(μ,Σ),Σ为m×m的半正定矩阵,对于非负整数s1,…,sm,有
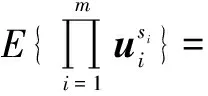
(20)
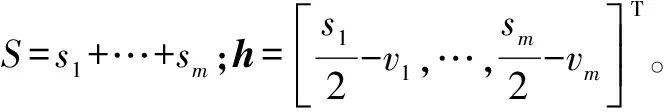
针对新观测方程,将零均值高斯白噪声设为在初始时刻的观测向量误差u=[ux1,ux2,uy1,uy2]T,并且该误差满足独立同分布,则
(21)
R=E[VVT]=σ2H(x1,x2,y1,y2)H(x1,x2,y1,y2)T+
diag(0,0,σ4,σ4,2σ4)
(22)
式中,H(x1,x2,y1,y2)是h(x1,x2,y1,y2)的Jacob阵。
由式(21)、式(22)可以看出,利用泰勒展开公式求解观测误差协方差阵的过程较为复杂,一旦量测方程的表达式发生变化,相应的误差协方差阵也需要作出调整。
3.2 基于迭代思想的UKF算法
滤波算法是跟踪过程中的重要环节,经典算法有UKF和PF。其中,UKF算法运算时间适中,跟踪精度较高且应用较广,但是在应用过程中也存在一些问题,比如,跟踪时有时存在收敛性不佳的缺点,表现为跟踪误差忽高忽低。为改善UKF算法收敛性,同时提高跟踪精度,本文提出基于迭代思想的UKF算法,其迭代步骤如下所述。
2) 令j=1,重新生成Sigma点
(23)
式中,λ为采样间隔系数。
3) 预测新状态与协方差阵
(24)
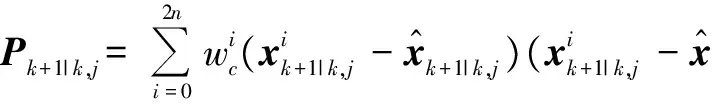
(25)
4) 预测观测值
(26)
(27)
5) 计算协方差矩阵和增益矩阵
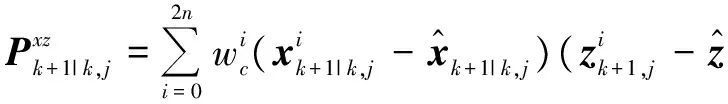
(28)
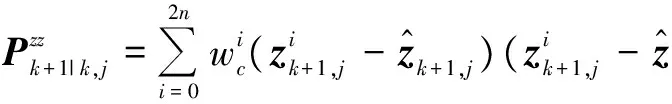
(29)
(30)
6) 更新状态和协方差阵
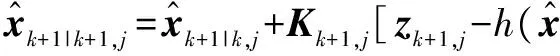
(31)
(32)
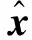
(33)
Pk+1|k+1=Pk+1|k+1,j。
(34)
4 仿真分析
在星下点为-30°E,30°E分别布置一颗GEO卫星,命名为GEO1和GEO2,两颗预警卫星对共同覆盖区域内出现的目标进行监视与跟踪,两个目标信息如表1所示。

表1 目标的发射参数
在两颗预警卫星的像平面上分别采用BPGM-SME算法进行跟踪,估计效果如图2所示。

图2 卫星像平面上估计效果图Fig.2 Satellite estimation on the plane of the rendering
由图2可以看出,在两颗预警卫星的像平面上两个目标的临近程度虽然有所差别,但采用BPGM-SME算法都能得到较好的跟踪效果。统计跟踪误差如图3所示。
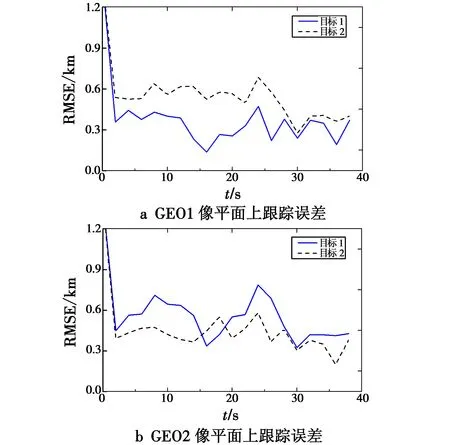
图3 跟踪误差图Fig.3 The tracking errors
从图3可看出,两颗卫星对同一个目标的跟踪误差有所不同,这是由目标与卫星的几何关系决定的,在GEO1像平面上,目标1的跟踪误差比目标2要小,但在GEO2像平面上,对目标2的跟踪效果比目标1要更好一些。根据前文设计的跟踪流程,将数据关联前置于像平面,因此,在像平面跟踪完毕后,各个目标在像平面上的位置就已经确定,而且可以用估计值代替观测值,从而转化为双星协同探测下的单目标跟踪。根据双星协同探测的跟踪流程,对两个目标的三维空间状态进行跟踪,目标真实位置以及跟踪结果如图4所示。
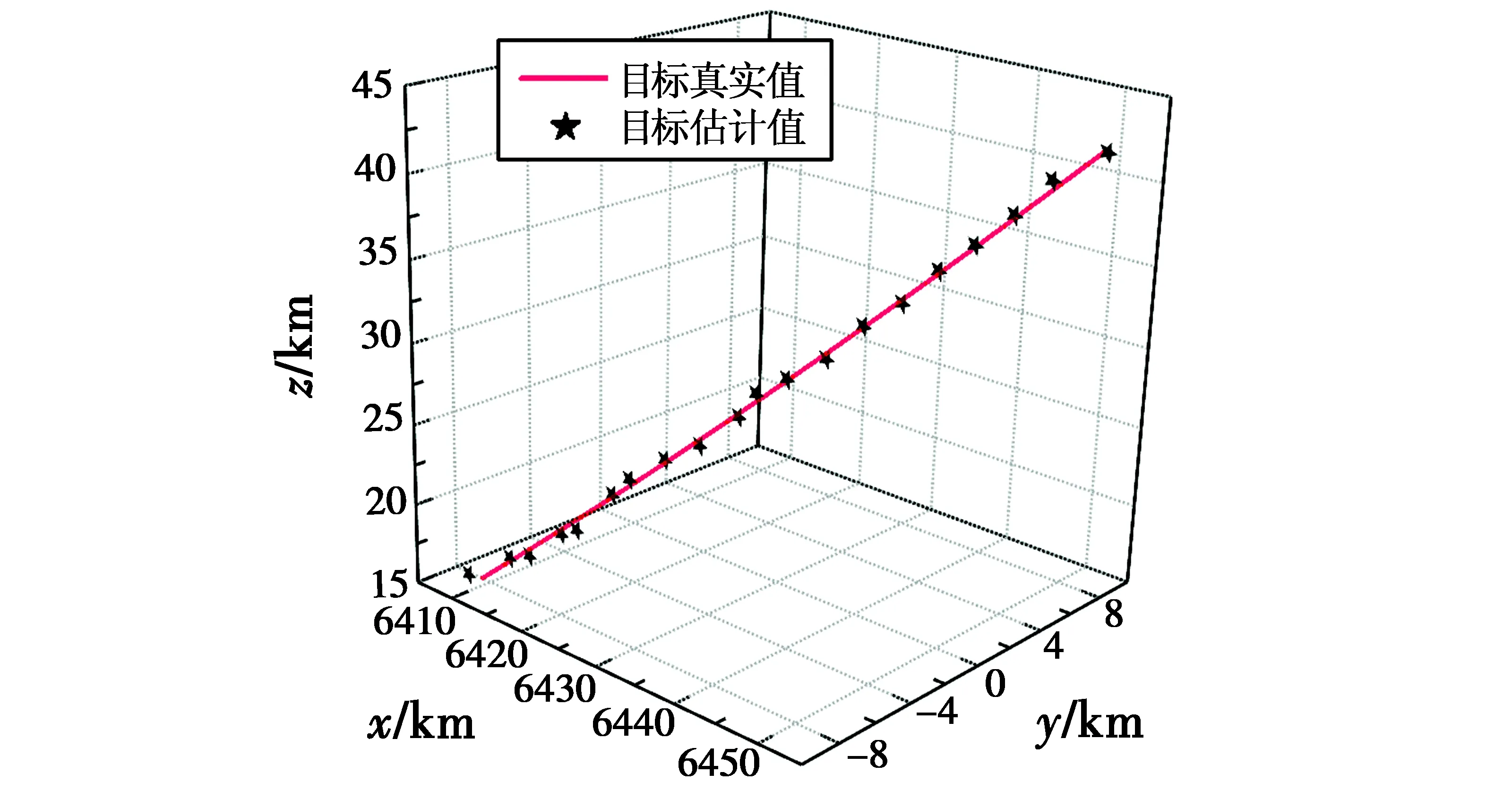
图4 目标真实值与估计值Fig.4 The real value and estimated value of targets
分别采用UKF和迭代UKF(IUKF)进行跟踪,跟踪误差如图5所示。
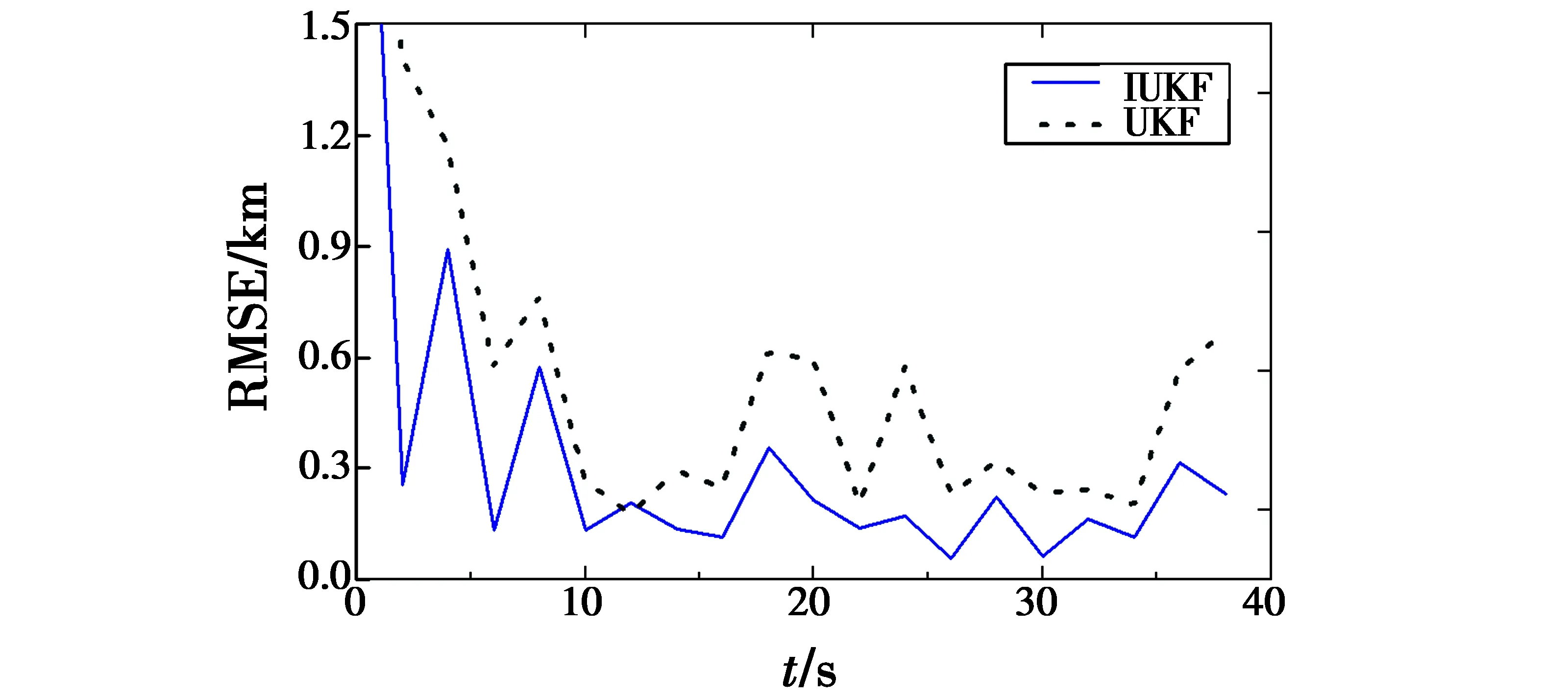
图5 各算法跟踪误差Fig.5 Tracking errors of different algorithms
从图4和图5可看出,基于双星探测的跟踪方法能够较为稳定地跟踪两个目标,并且两种滤波算法的跟踪精度都比较高,相比而言IUKF算法的收敛性更突出一些,因此,整体的跟踪精度也更高。
5 结论
本文为了解决双星协同探测对多目标跟踪的过程中目标航迹交叉和滤波算法的跟踪收敛性差问题,提出了基于二元多项式SME算法和迭代UKF滤波算法,仿真结果表明:
1) 当像平面观测过程中存在多目标航迹交叉时,采用BPGM-SME算法可以取得较好的跟踪效果;
2) 采用BPGM-SME算法对目标的跟踪过程中,跟踪效果好坏与目标和卫星间的几何关系有关;
3) 相比于传统的UKF算法,采用迭代UKF算法对目标进行跟踪时,在保证实时性的前提下,能够取得更好的收敛性效果和跟踪精度,能够满足预警卫星跟踪目标的实时性和精确性要求。
[1]KIM J,VADDI S S,MENON P K,et al.Comparison between nonlinear filtering techniques for spiraling ballistic missile state estimation[J].IEEE Transactions on Aerospace and Electronic Systems,2012,48(1):313-328.
[2]钟宇,吴晓燕,黄树彩,等.红外预警卫星弹道导弹主动段探测能力[J].红外与激光工程,2015,44(11):3276-3281.
[3]钟宇,吴晓燕,黄树彩,等.红外预警双星弹道导弹主动段跟踪性能[J].红外与激光工程,2015,44(12):3587-3596.
[4]王卫兵,王挺峰,郭劲.基于双星双目跟踪方式的空间目标定轨技术研究[J].光学学报,2015,35(1):0112006- 1-0112006-8.
[5]王卫兵,王锐,姜振华,等.天基监视中的双星相对运动模型研究[J].红外与激光工程,2015,44(12):3782-3787.
[6]LI X R,JILKOV V P.Survey of maneuvering target tracking part II: motion models of ballistic and space targets[J].IEEE Transactions on Aerospace and Electronic Systems,2010,46(1):96-119.
[7]邱昊,黄高明,左炜,等.基于标签随机有限集的多量测多目标跟踪算法[J].控制与决策,2016,31(9):1702-1706.
[8]BAUM M,NOACK B,BEULTER F,et al.Optimal Gaussian filtering for polynomial systems applied to association-free multi-target tracking[C]//Proceedings of the 14th International Conference on Information Fusion,2011:1-8.
[9]熊志刚,黄树彩,吴潇,等.基于改进遗传粒子滤波与SME 的多目标跟踪算法[J].火力与指挥控制,2016, 41(10):134-137.
[10]吴卫华,江晶,冯讯,等.基于随机有限集的多目标跟踪算法综述[J].电光与控制,2016,23(3):1-6.
[11]韩萍,桑威林,石庆研.一种新型非线性卡尔曼滤波方法[J].仪器仪表学报,2015,36(3):632-638.
[12]王硕,宋申民,于浛,等.基于组合导航系统的非线性高斯滤波算法[J].控制与决策,2016,31(9):1645-1653.
[13]张文,孙瑞胜.EKF与UKF的性能比较及应用[J].南京理工大学学报,2015,39(5):614-618.
[14]GUSTAFSSON F,HENDEBY G.Some relations between extended and unscented Kalman filters[J].IEEE Tran-sactions on Signal Processing,2015,60(2):545-555.
[15]李敏,王松艳,张迎春,等.改进的强跟踪平方根UKF在卫星导航中应用[J].系统工程与电子技术,2015, 37(8):1858-1865.
[16]TEIXEIRA B,CHANDRASEKAR J,TORRES L A B,et al.Unscented filtering for interval-constrained nonlinear systems[C]//IEEE Conference on Decision and Control,2008:5116-5121.
[17]叶有时,刘淑芬,孙强,等.改进粒子滤波算法在深空红外小目标跟踪中的应用[J].电子学报,2015,43(8):1506-1512.

