基于奇异值分解的Unscented粒子滤波及其应用研究
庞 策, 赵 岩
(空军工程大学防空反导学院,西安 710051)
0 引言
非线性滤波[1-3]是针对非线性系统,解决非线性问题的一种滤波方法,不需要将非线性问题进行线性化。常用的非线性滤波方法有:扩展卡尔曼滤波(EKF)[4]、中心差分卡尔曼滤波(CDKF)[5]、Unscented卡尔曼滤波(UKF)[6]、高斯-厄米特滤波(GHF)[7]和粒子滤波(PF)[8]等。Unscented粒子滤波(UPF)算法[9]吸收了UKF[4]和PF[1]算法的优点,被广泛用于非线性、非高斯动力学系统的参数估计和状态滤波问题。UPF算法
不仅克服了UKF算法不适用于非高斯噪声系统的局限性,而且克服了PF算法重要性密度函数难以选取的缺陷。但是,UPF算法仍易受到异常扰动的影响,且在计算迭代中可能出现协方差阵失去半正定性的问题。
针对UPF算法存在的问题,本文在UPF算法的基础上,提出基于奇异值分解的Unscented粒子滤波(SVD-UPF)算法。SVDUPF算法采用自适应因子调节动力学模型误差,通过奇异值分解抑制系统状态协方差矩阵的负定性,并以改进的UKF算法产生重要性密度函数,弥补粒子滤波重要性密度函数难以选取的缺陷。
1 奇异值分解原理
奇异值分解(SVD)是一种重要的矩阵分解方法,是矩阵分析中正规矩阵酉对角化的推广[10-11]。奇异值分解在某些方面与对称矩阵或Hermite矩阵基于特征向量的对角化类似,然而这两种矩阵分解尽管有其相关性,但还是存在明显的不同。对称阵特征向量分解的基础是谱分析,而奇异值分解则是谱分析理论在任意矩阵上的推广。
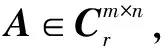
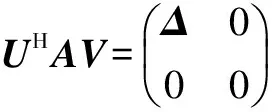
(1)
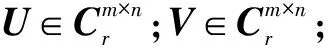
2 基于奇异值分解的Unscented粒子滤波算法
假设非线性系统
xk=f(xk-1)+wk-1
(2)
zk-1=h(xk-1)+vk-1
(3)
式中:xk为k时刻系统的n维状态向量;zk为m维量测向量;f(·)和h(·)分别为非线性状态转移函数和量测函数;wk为n维零均值过程噪声向量;vk为m维零均值量测噪声。
按照式(2)和式(3)所描述的非线性系统模型,设计基于奇异值分解的Unscented粒子滤波算法步骤如下所述。
1) 初始化。
从先验密度分布函数中抽取2n+1个样本点x0~p(x0),使
(4)
经扩维得
(5)
式中:Q0为状态转移方差;R0为观测噪声方差。权值为
(6)
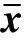
2) 构造自适应因子。
自适应因子函数选用两段函数自适应因子模型
(7)
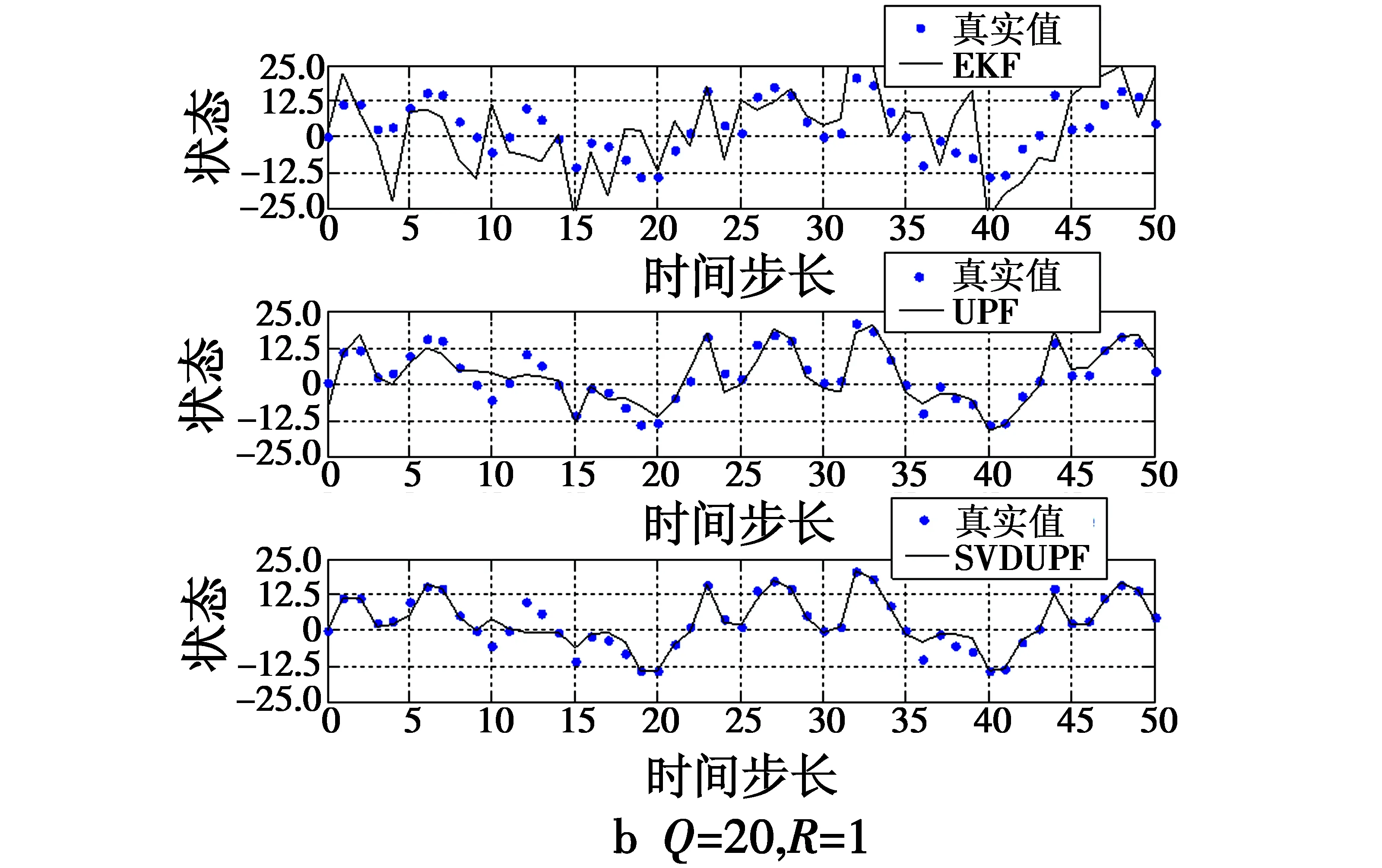
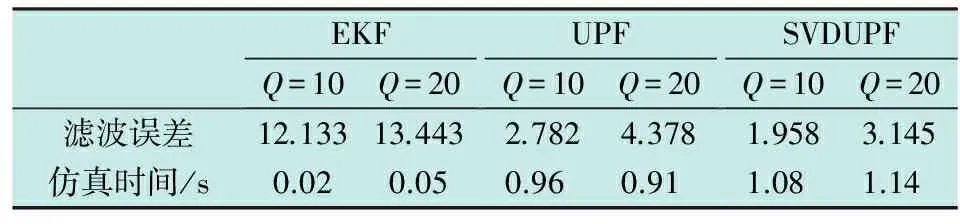
式中,αk表示自适应因子,c为经验常数,通常1 3) 奇异值分解,计算Sigma点集[12-13]。 分别计算特征点协方差矩阵和2n+1个Sigma点向量,即 (8) (9) 4) 时间更新。 χi,k|k-1=f(χi,k-1)+wki=0,1,…,2n (10) (11) (12) 式中,svd{·}为SVD分解算子。 (13) 式中,自适应因子αk由式(7)确定,并用αk修正σi,k|k-1。 χi,k|k-1= (14) (15) zi,k|k-1=h(χi,k|k-1)+vki=0,1,…,2n (16) (17) 式中,Q为系统噪声方差。 5) 量测更新。 (18) (19) (20) (21) (22) 式中,R为量测噪声方差。选择重要性函数为 (23) 6) 从建议分布函数中抽取粒子,并进行权值更新与归一化 (24) (25) 得到归一化权值 除了采用了一些常用的统计方法外,还进行了动力学诊断。这里计算了大气视热源 (26) 7) 计算估计值和方差。 (27) (28) 引理1假设动力学模型为 (29) 存在非线性函数f(·),使得先验分布和状态值的后验分布满足 (30) 证明设先验分布和状态值的后验分布分别为 ppr=p(X) (31) ppo=p(X|Z)。 (32) 根据贝叶斯递推预测理论 (33) 那么由函数内积可知,对于任意函数f(·),有 (34) (35) 那么必有 (36) 证明根据引理1 (37) 对式(37)进行如下运算 (38) 由于ppr(k|k-1)和f(·)均为概率密度函数,则 ‖ppr(k|k-1)f‖≤‖f‖ (39) 那么 (40) 引理3存在函数f(·)和h(·),使得先验分布和状态量的后验分布满足 (41) 证明根据贝叶斯递推更新理论 (42) 将非线性函数f(·)和ppo(k|k)做内积运算,由式(42)得到 (43) 定理1在k>0的情况下,必然存在独立于已知数N的常数c1,使得对于非线性函数f满足 (44) 证明根据引理1,2和3可知 (45) (46) 采用Minkowski不等式,得到 (47) (48) 由此说明该算法收敛。 将设计的算法应用到单变量非静态状态增长模型进行仿真。仿真的过程模型和观测模型为[14] x(t)=0.5x(t-1)+2.5x(t-1)/1+[x(t-1)]2+ (49) Z(t)=x(t)2/20+v(t) (50) 其中,w(t)和v(t)均为零均值高斯噪声,且方差分别为Q和R。 由于该系统具有高度非线性特征,似然函数呈现双峰分布,这种双峰性使得传统滤波方法难以处理。因此,采用提出的基于奇异值分解的Unscented粒子滤波(SVDUPF)与现有的EKF,UPF算法进行比较。仿真粒子数选为100,初始值取x(0)=0.1,P(0)=2,过程噪声Q和量测噪声R的方差选取两组数值,分别为Q=10,R=1和Q=20,R=1。仿真结果及数据比较如图1、表1所示。 图1 SVDUPF与现有算法对比Fig.1 Contrast between SVDUPF and current algorithms 从图1可知,SVDUPF算法的状态估值精度优于其他两种滤波算法得到的状态估值精度。说明SVDUPF算法在这些滤波算法中具有较高的滤波精度,UPF算法次之,EKF滤波精度最低。另外,当Q=10,R=1时(图1a)与Q=20,R=1时(图1b)相比较,设计滤波的状态估值随着过程噪声的增加而降低,说明滤波精度下降,但SVDUPF滤波精度下降较小,说明该算法能够抑制过程噪声。从仿真时间可以看出,SVDUPF算法其复杂度高于EKF和UPF算法,算法精度的提高是以复杂度的提高为代价的。 表1 仿真结果数据比较 本文提出一种改进UPF算法,即基于奇异值分解的Unscented粒子滤波算法。首先介绍了奇异值分解原理,并在此基础上,设计并提出了SVDUPF算法。将提出的算法应用于单变量非静态状态增长模型进行仿真验证,结果表明,提出算法的滤波性能明显优于EKF和UPF算法,能抑制模型误差,提高滤波解算的精度。 [1]DENG H,ZHANG D D,WANG T Y,et al.Objective image-quality assessment for high-resolution photospheric images by median filter-gradient similarity[J].Solar Physics, 2015,290(5):1479-1489. [2]DOUCET A,JOHANSEN A M.A tutorial on particle filtering and smoothing:fifteen years later[M].Oxford:Oxford University Press,2011:656-704. [3]HAUG A J.Bayesian estimation and tracking:a practical guide[M].New York:Wiley & Sons,Inc.,2012. [4]BUCY R S,SENNE K.Digital synthesis of nonlinear filter[J].Automatica,1971,7(3):287-289. [5]NØRGAARD M,POULSEN N K,RAVN O.New developments in state estimation for nonlinear systems[J].Automatica,2000,36(11):1627-1638. [6]LEFEVRE T,BRUYNINCKX H,DE SCHUTTER J.Comment on“a new method for the nonlinear transformation of means and covariances in filters and estimators”[J].IEEE Transactions on Automatic Control,2015,47(8):1406-1409. [7]LERROR D,BAR-SHALOM Y.Tracking with debiased consistent converted measurements versus EKF[J].IEEE Transations on Aerospace and Electronic Systems,1993, 29(3):1015-1022. [8]JULIER S,UHLMANN J,DURRAN-WHYTE H F.A new method for the nonlinear transformation of means and covariances in filters and estimators[J].IEEE Transactions on Automatic Control,2000,45(3):477- 482. [9]杨小军,潘泉,王睿,等.粒子滤波进展与展望[J].控制理论与应用,2006,23(2):261-267. [10]PATEREK A.Improving regularized singular value decomposition for collaborative filtering[C]//Proceedings of KDD Cup and Workshop,2007:5-8. [11]ALTER O,BROWN P O,BOTSTEIN D.Singular value decomposition for genome-wide expression data processing and modeling[J].Proceedings of the National Aca-demy of Sciences,2000,97(18):10101-10106. [12]高社生,桑春萌,李伟.改进的粒子滤波在列车组合定位系统中的应用[J].中国惯性技术学报,2009,17(6):701-705. [13]高社生,王建超,焦雅林.自适应SVD-UKF 算法及在组合导航的应用[J].中国惯性技术学报,2010,18(6):737-742. [14]杨元喜.自适应动态导航定位[M].北京:测绘出版社,2006.
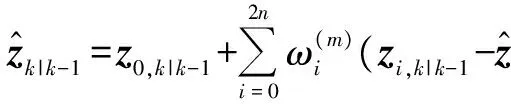
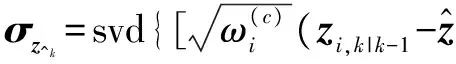
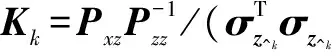
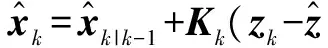
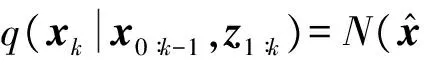
3 算法收敛性分析
4 仿真分析
8cos[1.2(t-1)]+w(t)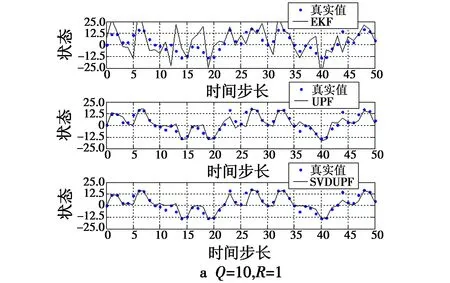
5 结论

