密云水库上游径流变化趋势及影响因素

秦丽欢,周敬祥,李叙勇,曾庆慧

1 中国科学院大学,北京　100049 2 中国科学院生态环境研究中心, 城市与区域生态国家重点实验室,北京　100085 3 中交水运规划设计院有限公司,北京　100007

河川径流的变化是气候、地貌、土壤及人类活动共同作用的结果[1]。分析河川径流量的时间变化特征、周期规律以及影响因素,对了解水资源特性,从而更好的开发利用水资源有重要的意义[2]。尤其我国北方地区,水资源已是制约社会经济发展的关键因素[3]。密云水库是北京市目前唯一的地表饮用水源地,上游入库径流的变化对其水量有重要的影响,分析评价密云水库入库径流的年际变化及周期性演变趋势、识别影响径流变化的因素对优化密云水库水资源调度,可为北京市饮用水保障提供有利的科学依据。

目前对密云水库上游流域展开的研究采用的方法主要有统计经验公式法[4]、水文模型法,分为集总式模型[5]和分布式模型[6]。Li等[4]采用M-K检验的方法分析了潮河流域降雨和径流的变化趋势,表明人类活动对径流变化产生重要的影响；孙宁等[5]利用IHACRES 模型分析了土地利用变化和覆被对潮河流域径流的影响,结果表明,土地利用和覆被变化减少了流域年径流；郭军庭等[6]利用SWAT模型分析了潮河流域径流对气候变化和土地利用变化的响应特征,结果表明,气候变化对年径流量的影响较大。

然而这些研究将研究区域集中在潮河流域[5-7],对白河流域径流特征的研究较少。特别是对影响密云水库径流量的影响因素仍然存在争议,Wang等[8]认为潮白河流域1980年前后径流减少的主要原因是人类活动(68%—70%),而气候变化是次要原因(30%—32%)。因此,人类活动对潮河流域径流减少起决定因素。而Ma等[9]认为潮白河流域径流下降的原因主要是气候变化(55%—51%),而人类活动对径流下降的影响只有18%。特别是密云水库担任南水北调进京水量调蓄的重要任务,通过对上游来水量的径流特征深入了解,对南水北调入库流量的科学调度有重要的意义。因此。有必要对密云水库白河和潮河流域的径流变化趋势和影响因素进行分析和比较,这对高效和合理管理密云水库有重要作用。

1　研究区域概况

密云水库(40°29.0′—40°30.5′N, 116°50.0′—117°3.5′E)位于北京北部,建成于1960年,是以综合防洪、供水为目的的大型水利工程[10],总库容为43.7亿m3[11]。白河和潮河是密云水库主要的入库河流(图1),其中,白马关河、蛇渔川河是白河的主要支流；红门川河、清水河、安达木河、虻牛河、汤河是潮河的主要支流。安达木河上建有遥桥峪水库,虻牛河中游建有半城子水库。流域控制流域面积15788km2,属于半干旱半湿润的大陆性季风气候,降水主要分布在汛期(7—9月),占总降水量的80%。流域的主要土壤类型为褐土和棕壤,主要植被覆盖类型是针阔叶混交林[12]。

图1　密云水库位置图Fig.1　The location of Miyun Reservoir

2　数据来源和研究方法

2.1　数据来源

径流量资料来源于密云水库管理处,包含白河与潮河的流域出口张家坟和下会两个水文站的月径流资料,径流系列长度为1960—2014年。

2.2　研究方法

本文采用的研究方法包括不均匀系数法分析年内径流量的变化趋势,利用滑动平均法分析径流量的年际变化趋势,采用M-K突变分析法确定径流突变点,利用Molert小波分析50年来密云水库径流的周期性变化,并通过对周期性的显著性检验,确定主周期。利用降水-径流双累积曲线分析和揭示降水和人类活动对径流的影响阶段性变化,从而得到降水变化和人类活动变化对径流的贡献,具体流程见图2。

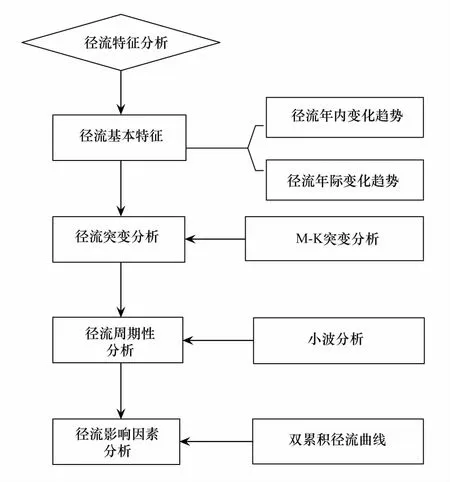
图2　密云水库径流特征分析流程图Fig.2　The flow chart of the analysis method of Miyun runoff

2.2.1年内变化

径流量年内不均匀系数可以通过公式(1)—公式(3)进行计算。

(1)

(2)

(3)

式中,Raverage为月平均径流量(亿m3),Ri为第i月的径流量(亿m3),σ为均方差系数

2.2.2年际变化

水文序列的随机波动性使得难以从序列本身判断出其变化趋势。滑动平均法可以消除波动的影响,通过对原序列的光滑化处理,即对序列的几个前期值和后期值取平均,得到新的序列,通过新序列判断水文变化的趋势性具有直观和明显的优势[13]。利用公式(4)进行计算。

(4)

式中,k为滑动长度,j=(1,2,3,…,n-k+1)

2.2.3突变分析-Mann-Kendall 非参数统计检验

Mann-Kendall 非参数统计检验方法,可进行径流量趋势的检验,其优点在于样本不必遵循某一特定规律,也不受个别异常值干扰,能客观表征样本序列的整体变化趋势[14]。

设某一时间序列Xi具有n个样本量,构造该时间序列的秩序列：

(5)

式中：

(6)

秩序列Sk表示第i时刻序列值大于j时刻序列值的个数之和。当x1,x2,…,xn相互独立且连续同分布时,定义统计量：

(7)

(8)

(9)

式中,k=2,…,n;n为样本数；UFk为M-K统计量,且UF1= 0且UFi服从正态分布；E(Sk) 和Var(Sk) 分别是累计数Sk的均值和方差。

取显著水平а,若|UFi|>Ua(其中,U0.05=±1.96,U0.01=±2.57),则说明序列趋势线显著。UFi为正时,表明序列呈上升趋势,否则呈下降趋势,且其绝对值越大表明序列变化趋势越显著。将时间序列逆序,重复M-K的计算过程,得到逆序列M-K统计值UBk, 当统计量序列曲线出现交点,且交点在临界线之间时,此时交点所在的年份即为可能发生突变的时间[15]。

2.2.4周期性变化

由于水文演变时序是多时间尺度的持续过程[16],而传统的分析水文要素周期变化特征的方法对揭示其多时间尺度特征存在局限性,不能揭示水文要素多时间尺度的特征[13],而小波分析在研究不同时间尺度变换及对信号的自适应方面具有优势。因此采用小波分析的方式确定密云水库白河与潮河入库径流量的周期性变化。主要的小波函数有Daubechies小波、Meyer小波、Mexicanhat小波、Symlet小波、Morlet小波等[17]。其中Morlet小波在水文周期性序列上较为常用[18]。Morlet小波函数为复数小波,表达式如下[19]：

Ψ(t)=eicte-t2/2

(10)

式中：c为常数,i为虚部。小波变换是对于基本小波函数做位移后,再对不同尺度时域下的需要进行分析的信号做内积。任意函数f(t)∈L2(R),L2(R)表示平方可积的实数空间。f(t)连续小波变换的表达式为公式(11)

(11)

Wf(a,b)小波变化系数随a,b变化,可作出以b为横坐标,a为纵坐标的二维小波系数Wf(a,b)等值线图。而正负小波系数的突变点则为突变点。在时间域上对关于a的所有小波系数的平方进行积分,得到小波方差,见公式(12),反映了波动能量在时间尺度的分布情况,从而确定时间序列下的主周期[19]。

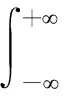
(12)

2.2.5双累积曲线法

双累积曲线是研究两个参数间的关系一致性及变化的常用方法。通过在直角坐标系中绘制一个变量的连续累积值与另一个变量的连续累积值的关系线,分析获得两参数间关系的一种常用的分析方法[20]。其斜率的变化可以作为变量间关系发生变化的指示,拐点出现的时间则为变量间关系发生明显变化的年份[7]。该方法是目前在水文气象要素一致性或长期演变趋势分析中最简单、直观和广泛应用的分析方法[18]。当只有降水的变化而无其他因素影响时,降雨-径流双累积曲线应为一条直线,而当有人类活动等其他因素影响时,曲线将发生偏移。因此,可根据曲线发生偏移的年代确定下垫面受人类活动影响的时间,而根据偏移程度可推断人类活动对径流影响的剧烈程度。因此,降雨-径流的双累积曲线可以反应人类活动对径流影响的阶段性特征[21]。

双累积曲线具体的计算过程如下[22]：

(1)首先将双累积曲线斜率未发生偏移的时期作为未受人类活动干扰的基础期,建立基准期降雨量∑P和累积径流量∑Q的相关方程(13)：

∑P=k∑Q+b

(13)

(2)在假设变化期与基准期的气候变化同步的前提下,公式(14)得到的变化期模拟径流与实测径流的差值即为径流受人类活动影响的变化量

ΔQhuman=mean(Q2c)-mean(Q2m)

(14)

(3)变化期实测径流与基准期实测径流的差值为径流受气候变化与人类活动共同影响的变化量由公式(15)可得

ΔQ=mean(Q2m)-mean(Q1c)

(15)

(14)、(15)式中,下标c、m分别代表模拟值和实测值,1,2分别代表基准期和变化期。

3　结果与分析

3.1　径流量的年内和年际分配特征

3.1.1年内不均匀系数

图3展示了密云水库潮河与白河的水文监测站点1960—2014年的入库平均径流流量。张家坟和下会水文站径流量的季节性变化特征一致,主汛期7—9月份径流量较大,在12.3—39.1m3/s之间；而其他月份径流量则在1.3—12.0m3/s之间。两个站作比对,可见张家坟站的月平均流量为8.28m3/s是下会站的月平均流量为5.71m3/s的1.45倍。

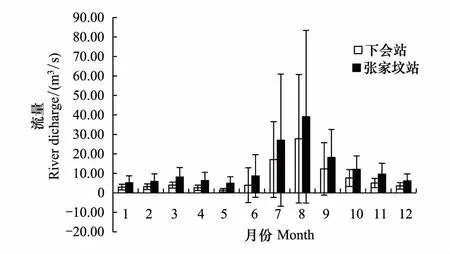
图3　年张家坟和下会站月平均流量Fig.3　The monthly runoff of Zhang Jiafen and Xiahui station

利用不均匀系数可以有效反应径流量的年内分配特征。图4展示了张家坟站和下会站不均匀系数计算结果。张家坟站不均匀系数波动性较大,在0.20—1.80之间,说明该站径流量的年内变化较大,而下会站径流的不均匀系数在0.04—0.68之间。潮河流域的入库径流年内变化比白河流域入库径流小,不均匀系数显著相关(P<0.01)。

3.1.2年际变化

利用5年滑动平均[23]分别对下会站和张家坟站径流量的年际变化进行分析,如图5、图6所示。50年来,白河流域和潮河流域入库量在线性趋势上上有减少的趋势,而在20世纪70年代和20世纪90年代的径流量有增加的趋势,20世纪60年代、80年代和2000年以来径流量有减少趋势。其中从图5、图6中可得,潮河流域和白河流域的入库径流量在1973年、1974年达到最大值,分别为28.1、42.4m3/s。而最小值两个水文站发生在2002年,其中下会站为1.86m3/s,张家坟站为2.2m3/s。密云水库50年来入库径流量呈减少趋势。

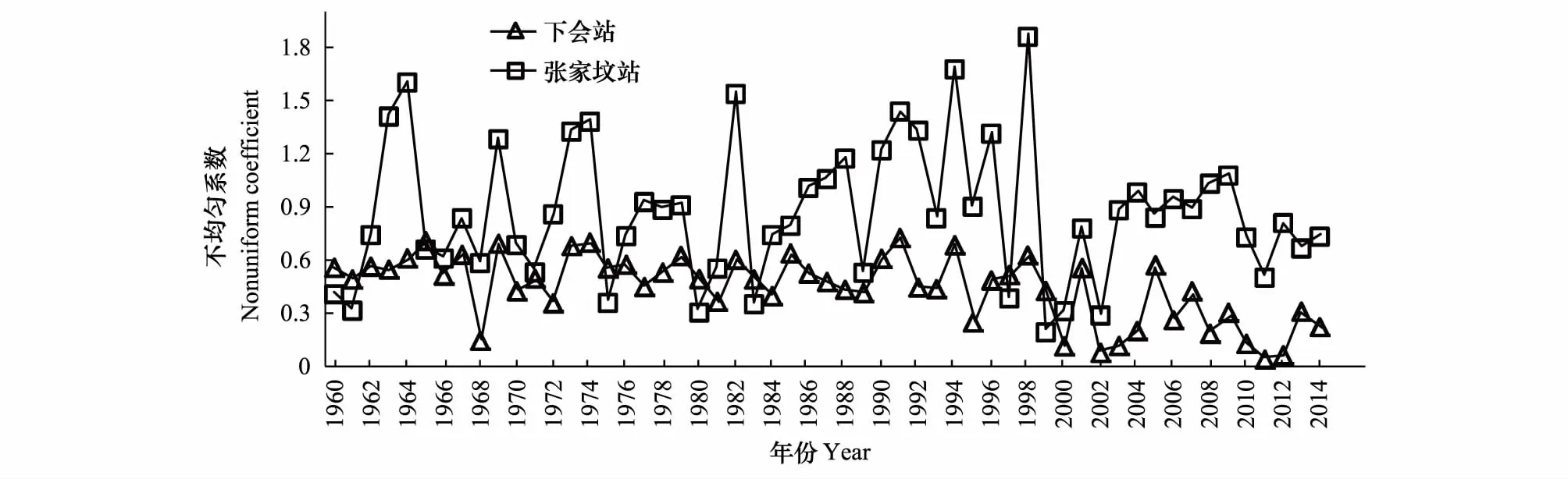
图4　1960—2014年张家坟和下会站不均匀系数Fig.4　Unevenness of annual runoff distribution of Zhang Jiafen and Xiahui Station from 1960 to 2014

图5　潮河流域年径流量变化及5年滑动平均Fig.5　Runoff variation of Chao River basin and 5a Moving-Average

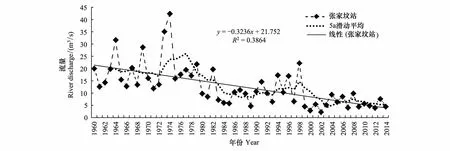
图6　白河流域年径流量变化及5年滑动平均Fig.6　Runoff variation of Bai River basin and 5a Moving-Average

3.2　突变分析

利用Mann-Kendall 法检验分析了在显著性水平α= 0.05下密云水库入库的水文站点张家坟站(白河)和下会站(潮河)1960—2014年径流变化趋势(图7,图8)。张家坟站和下会站径流分别在20世纪60年代初经历短暂的下降,然后进入径流量增加的阶段,该过程一直持续到20世纪80年代,随后径流量急剧下降,其中张家坟站在1987年发生突变,下会站则在在1998年发生突变。

图7　张家坟站径流Mann-Kendall 突变分析Fig.7　The Mann-Kendall abrupt change test on runoff of Zhang Jiafen StationUF:表示M-K顺序统计值; UB: 表示M-K逆序统计值

图8　下会站径流Mann-Kendall 突变分析Fig.8　The Mann-Kendall abrupt change test on runoff of Xiahui Station　UF:表示M-K顺序统计值; UB: 表示M-K逆序统计值

3.3　周期性变化

采用Morlet小波对密云水库白河和潮河流域50年来年径流量进行周期演变分析。分别得到白河张家坟站、潮河下会站小波变换系数实部图(图9,图11)和小波方差图(图10,图12)。小波系数的变化特征可以用来表征年径流量的变化特征。当小波系数实部为正值时,代表丰水期,负值代表枯水期,而小波系数实部为0时,则表示年径流从丰水期转为枯水期或由枯水期转为丰水期的转折点[24]。

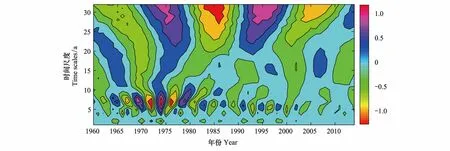
图9　白河流域张家坟站小波变换系数实部图Fig.9　The contours of the real part of Morlet wavelet coefficients of runoff in Bai River basin

由图9可见,白河流域年径流量变化主要存在5—8a,14—18a周期振荡。在5—8a的特征尺度下,丰枯交替特别频繁,并以7a为振荡中心。主要集中在20世纪60年代—20世纪90年代之间,其中20世纪60年代—20世纪80年代经历了强烈的丰-枯交替转变过程。14—18a特征尺度下,主要集中在20世纪90年代以后,震荡中心在17a左右。而通过图10,白河流域存在7a和14a两个主周期。其中在7a的小波方差值最大,是第一主周期。图11是潮河流域年径流量变化情况,主要存在5—8a的周期振荡,14—18a周期振荡不明显。与白河流域年径流量变化特征类似,在5—8a存在丰枯频繁交替的现象,以7a为振荡中心,在20世纪60年代—20世纪70年代经历了对比强烈的丰-枯交替转变过程。而结合白河流域年径流量小波方差图(图10),只存在7a的主周期,14a峰值并不明显。因此认为,白河流域年径流量第一主周期为7a。因此,对于白河和潮河两个密云水库主要入库河流来说,径流变化趋势既有类似之处同时也存在着差异。

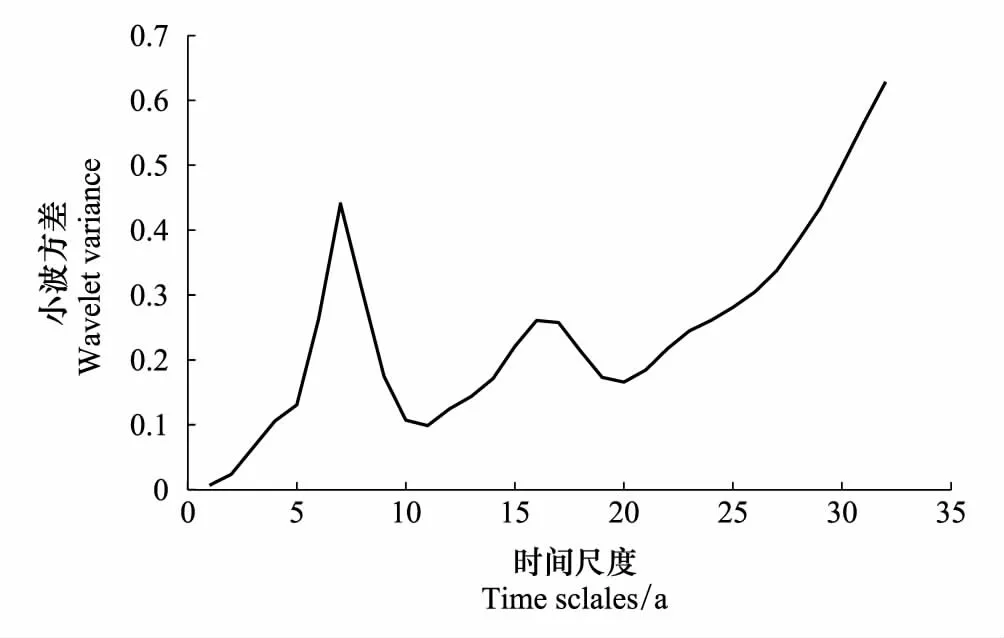
图10　白河流域张家坟站小波方差　Fig.10　The wavelet variances of annual runoff in Bai River basin

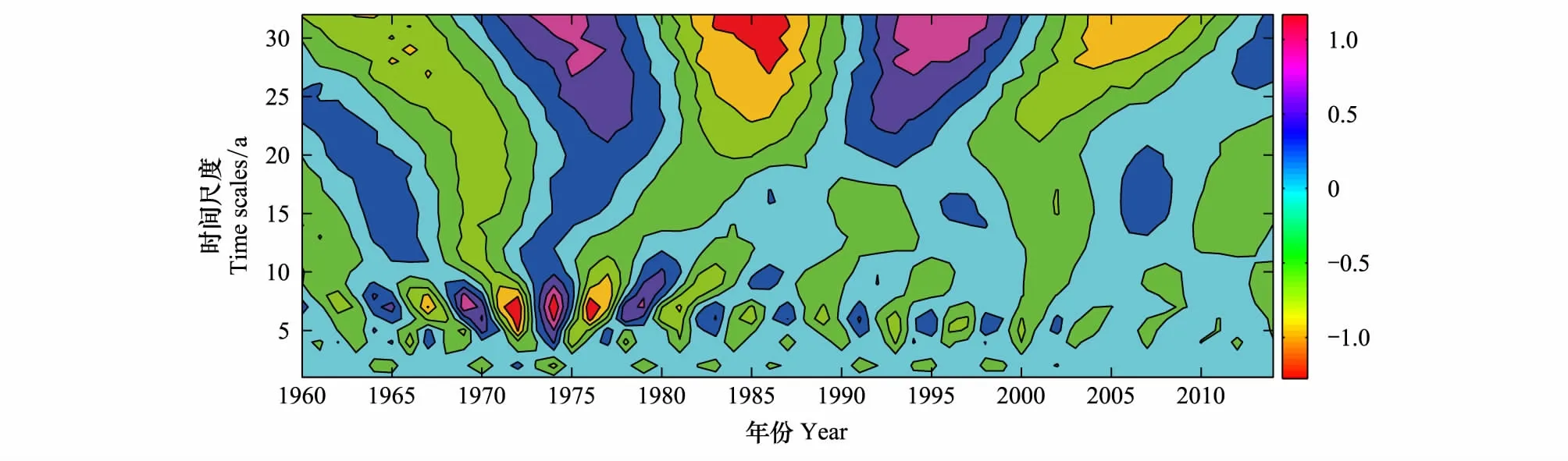
图11　潮河流域下会站小波变换系数实部图Fig.11　The contours of the real part of Morlet wavelet coefficients of annual runoff in Chao River basin

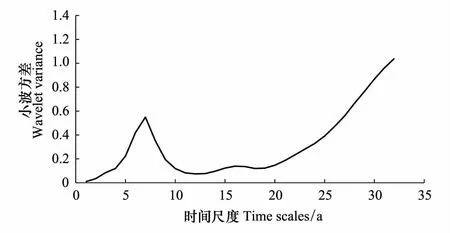
图12　潮河流域下会站小波方差　Fig.12　The wavelet variances of annual runoff in Chao River basin

3.4　密云水库入库径流量变化驱动因子分析

影响径流量的因素主要包含两个方面,一是自然因素,二是人类活动。自然因素主要包含地形、土壤等下垫面条件和气候条件,一般认为下垫面在一定时间尺度上是不发生改变的,因此自然因素主要考虑的是气候因素如降雨对径流量的影响。人类活动主要包括取用水、水利工程和土地利用等方面[25]。因此,采用了降水-径流双累积曲线对降雨和人类活动对密云水库入库径流量的影响进行分析。

图13为白河流域降水-径流双累积曲线。根据径流-降雨双累积曲线的斜率发生变化的位置确定1973年和1996年为突变点,将白河流域径流序列分为1960—1973年,1974—1996年,1997—2014年3个阶段。其中,第一阶段1960—1973年可以作为白河流域径流序列的基准期。从三阶段的降水-径流双累积曲线的拟合方程中,双累积的曲线斜率从基准期的0.871下降到0.300,衰减率为65.5%,表明人类活动对白河流域的径流产生极大的影响。图14是潮河流域降雨-径流双累积曲线。同白河流域径流趋势类似,潮河流域下会站的径流曲线突变点为1972年和1997年,将第一阶段1960—1971年作为基准期,其他两个阶段表示了人类活动对径流的影响。通过对双累积曲线方程进行线性拟合,得到各阶段双累积曲线的斜率,潮河流域基准期的斜率为0.4443而第三阶段的斜率则下降至0.1469,衰减率为66.9%。可见人类活动对潮河流域径流同样有巨大的影响。表1列出了人类活动及降雨对密云水库白河和潮河流域径流量的影响。表明潮河流域和白河流域径流量有减少趋势。白河流域入库流量从1960—1973年的5.98亿m3,减少到1997—2014年的2.07亿m3,减少了65.38%。而潮河流域入库流量则从3.2亿m3(1960—1971年)减少到1.19亿m3(1998—2014年)减少了62.81%。白河流域入库径流量减少幅度更为明显。通过对潮白河流域突变期的分析,分别得到了降雨和人类活动对入库径流的影响比例(表1)。降雨和人类活动对白河入库两个突变期的径流的影响在8.21%、10.10%和91.90%、89.90%；对潮河流域的影响分别在22.60%、27.64%和77.40%、72.36%。因此,人类活动可能是导致密云水库入库径流减少的主要因素。

图13　白河流域张家坟站双累积径流曲线Fig.13　Double mass curve of the precipitation and runoff in Bai River

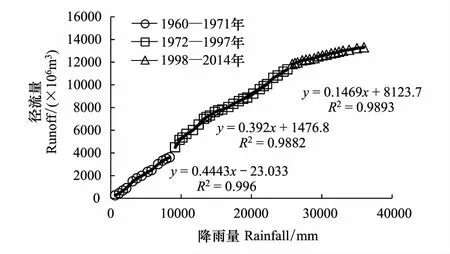
图14　潮河流域下会站双累积径流曲线图Fig.14　Double mass curve of the precipitation and runoff in Chao River

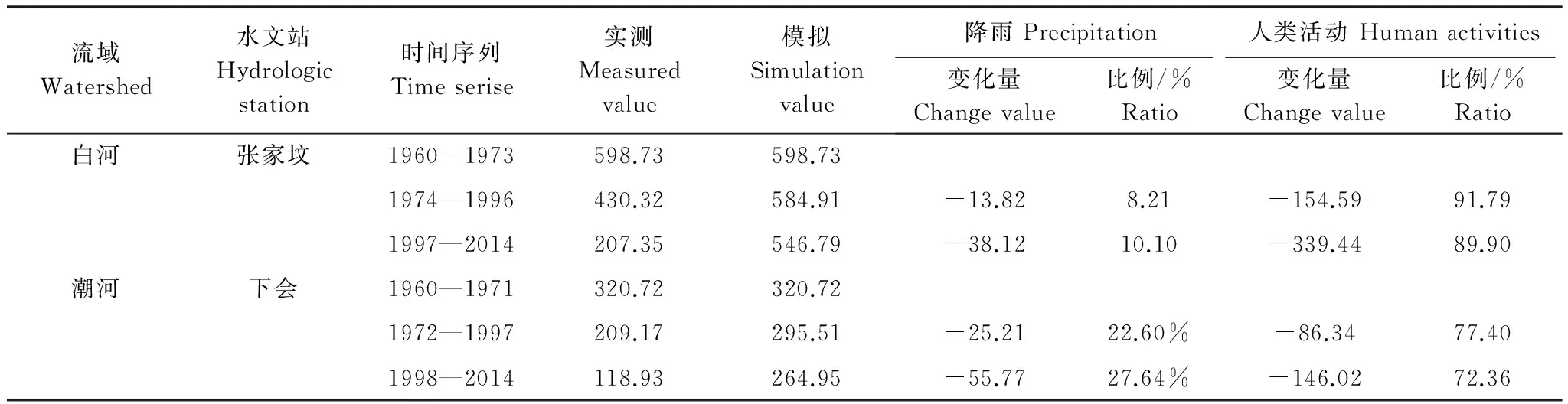
流域Watershed水文站Hydrologicstation时间序列Timeserise实测Measuredvalue模拟Simulationvalue降雨Precipitation人类活动Humanactivities变化量Changevalue比例/%Ratio变化量Changevalue比例/%Ratio白河张家坟1960—1973598.73598.731974—1996430.32584.91-13.828.21-154.5991.791997—2014207.35546.79-38.1210.10-339.4489.90潮河下会1960—1971320.72320.721972—1997209.17295.51-25.2122.60%-86.3477.401998—2014118.93264.95-55.7727.64%-146.0272.36

4　讨论

4.1　降雨对径流影响分析

密云水库白河流域和潮河流域径流具有年内分配不均匀的特性,在年际变化中径流量有缓慢减少的趋势。高迎春等[26]研究以长时间序列降雨和径流的数据进行分析,发现随着时间的向后推移,降雨与径流之间的关系逐渐减弱。而降雨在相同时间尺度上并没有发生明显的变化,降雨对径流的影响比例变化不大(如白河流域从第二阶段的8.21%变化为第三阶段的10.10%)(表1),从这一方面可以推断,降雨可能不是影响径流量变化的关键因素。根据表1中结果,降雨对潮河流域径流减少的影响在1974—1996年和1997—2014年两个阶段分别为22.60%和27.64%。李子君和李秀彬[27]通过分析降雨和径流变化的一致性也得到密云水库潮河流域径流减少受降雨影响较小的结论。而对降雨对白河流域的影响1974-1996年和1997—2014年两个阶段分别为8.21%和10.10%。王静怡等[28]同样通过分析入库径流和降雨的关系中进一步断定,降雨不是决定径流变化的单一因素。王巧平等[29]在海河流域研究了人类活动对径流的影响,结果表明,降雨能够影响该流域径流量的减少,但不是主要因素。对海河流域而言,降雨主要集中在7、8月份,产流也主要由汛期的几次大的降雨形成,影响产流的因素主要来自于土壤吸水、植物蒸散发,填洼等损失。由于雨期的蒸发量可以忽略不计,而下垫面的变化对降雨的影响可以忽略不计,因此,地表径流的变化主要来自人类活动引起地表植被改变蒸腾作用的等方面的影响。

4.2　人类活动对径流影响分析

人类活动如土地利用变化、水库的拦截以及跨流域的水库补水是导致径流变化的主要原因。如表1中所示,人类活动对白河流域、潮河流域影响分别在89.90%—91.79%和72.36%—77.40%。通过对流域内赤峰县、丰宁县和滦平县的人类活动用水量进行统计,发现1985—2015年间用水量呈增加趋势,总用水量从0.02亿m3增加到0.14亿m3[12]。因此流域用水量的增加,导致潮白河径流量的减少。同时,密云水库流域从1990—2010年间,土地利用类型发生了重大的转变,农田、草地和水体的面积分别减少了30%、48%、61%,林地增加了30%。由于林地相比农田和草地具有较强的水分蒸腾作用,导致径流量减少[30]。而小流域的综合治理提高了植被覆盖率,增加了植被的截流量,因此植物截留量、土壤持水量及蒸散发量等的增大,使得径流量减少[29],与此同时,密云水库上游有26座水库,总库容达1.325亿m3[31],水库会在一定程度上增加蒸发损失和渗漏量,从而减少径流量。除此之外,流域内水库向流域外调水,也在一定程度上减少径流。如白河流域的白河堡水库承担防洪灌溉的功能外,还向流域外的官厅水库补水,平均每年补水量达0.78亿m3；向十三陵水库平均每年补水0.1m3[25],这样向流域外水库补水的过程,在一定程度上减少潮白河流域的径流量。

4.3　南水北调重大调水工程影响下,密云水库水量调度的启示

密云水库在南水北调工程中起到了对进京水量调蓄的作用,并于2015年9月开始接纳南水进入,蓄水量得到了明显的补给,水位一度上升至140m。南水北调之水进入密云水库,一方面缓解了水库的供水压力,有效补充了水库的水量,另一方面也为水库运行带来风险。通过对上游径流变化特征的研究,将其与南水北调入库调蓄流量结合起来,丰水年的汛期结合小调水量,枯水年非汛期结合大调水量。这样可以有效协调和发挥上游入库径流和南水北调之水的特性和优势,保证密云水库正常的蓄水供水功能。

5　结论

潮河和白河作为密云水库上游两条主要的入库河流,对密云水库有重要的影响和作用。本文分别对潮河流域和白河流域径流进行了分析比较,结论如下：

(1)从50年径流数据中可以看出,潮河与白河的径流量年内分配不均匀的情况,主要的径流量多集中在汛期(7—9月),汛期径流量占全年比例70%。与潮河流域径流量相比,白河流域的年内变化更为剧烈,径流量减少趋势更为明显。

(2)白河与潮河流域径流都具有周期性的变化,其中白河流域径流存在7a和17a的周期,而潮河流域径流周期为7a。

(3)通过对降雨和人类活动对密云水库径流量的影响分析,结果表明白河流域径流受到人类活动变化更为剧烈。

参考文献(References):

[1]乔木, 周生斌, 卢磊. 艾比湖流域年径流变化特征分析. 水土保持学报, 2010, 24(6): 236-239.

[2]刘艺, 雷晓云, 马红刚, 邢坤, 吕姣姣. 巴音沟河近60年出山口年径流量演变规律. 水土保持研究, 2016, 23(2): 139-142.

[3]魏玲玲, 李万明. 干旱区水资源与经济发展要素时空匹配实证——以新疆地区为例. 求索, 2014, (3): 55-59.

[4]Li Z J, Li X B, Xu Z M. Impacts of water conservancy and soil conservation measures on annual runoff in the Chaohe River Basin during 1961-2005. Journal of Geographical Sciences, 2010, 20(6): 947-960.

[5]孙宁, 李秀彬, 李子君, 余新晓. 潮河上游土地利用/覆被变化对年径流影响模拟. 北京林业大学学报, 2008, 30(S2): 22-30.

[6]郭军庭, 张志强, 王盛萍, Peter S, 姚安坤. 应用SWAT模型研究潮河流域土地利用和气候变化对径流的影响. 生态学报, 2014, 34(6): 1559-1567.

[7]杨默远, 桑燕芳, 王中根, 刘昌明. 潮河流域降水—径流关系变化及驱动因子识别. 地理研究, 2014, 33(9): 1658-1667.

[8]Wang G S, Xia J, Chen J. Quantification of effects of climate variations and human activities on runoff by a monthly water balance model: a case study of the Chaobai River basin in northern China. Water Resources Research, 2009, 45(7): W00A11, doi: 10.1029/2007WR006768

[9]Ma H, Yang D W, Tan S K, Gao B, Hu Q F. Impact of climate variability and human activity on streamflow decrease in the Miyun Reservoir catchment. Journal of Hydrology, 2010, 389(3/4): 317-324.

[10]钟永华, 鲁帆, 易忠, 赵静. 密云水库以上流域年径流变化趋势及周期分析. 水文, 2013, 33(6): 81-84.

[11]段新光, 郝丽娟, 栾芳芳. 密云水库流域降水量与径流量特征分析. 北京水务, 2013, (1): 38-41.

[12]李子君, 李秀彬. 潮白河上游1961—2005年径流变化趋势及原因分析. 北京林业大学学报, 2008, 30(S2): 82-87.

[13]郭亚男. 岚河流域径流变化规律及其影响因素分析[D]. 郑州: 郑州大学, 2013.

[14]周婷, 于福亮, 李传哲, 柴增凯. 1960—2005年湄公河流域径流量演变趋势. 河海大学学报: 自然科学版, 2010, 38(6): 608-613.

[15]张跃华, 徐刚, 张忠训, 杨海燕. 嘉陵江年径流量时间序列趋势分析. 重庆师范大学学报: 自然科学版, 2011, 28(5): 33-36.

[16]刘晓琼, 刘彦随, 李同昇, 孟欢欢, 于正松, 芮旸. 基于小波多尺度变换的渭河水沙演变规律研究. 地理科学, 2015, 35(2): 211-217.

[17]汤成友, 缈韧. 基于小波变换的水文时间序列分解及周期识别. 人民长江, 2006, 37(12): 32-34.

[18]安全, 梁川, 刘政. 雅砻江中上游径流变化特性的小波分析. 武汉大学学报: 工学版, 2008, 41(3): 20-24, 28-28.

[19]古丽孜巴·艾尼瓦尔, 麦麦提吐尔逊·艾则孜, 米热古丽·艾尼瓦尔, 麦尔丹·阿不拉. 基于小波分析1956-2010年焉耆盆地清水河径流量季节变化规律. 水土保持研究, 2016, 23(1): 210-214, 220-220.

[20]穆兴民, 张秀勤, 高鹏, 王飞. 双累积曲线方法理论及在水文气象领域应用中应注意的问题. 水文, 2010, 30(4): 47-51.

[21]侯钦磊, 白红英, 任园园, 贺映娜, 马新萍. 50年来渭河干流径流变化及其驱动力分析. 资源科学, 2011, 33(8): 1505-1512.

[22]邱玲花, 彭定志, 林荷娟, 张明月, 房晶. 气候变化与人类活动对太湖西苕溪流域水文水资源影响甄别. 水文, 2015, 35(1): 45-50.

[23]赵阳, 余新晓, 郑江坤, 武巧英. 气候和土地利用变化对潮白河流域径流变化的定量影响. 农业工程学报, 2012, 28(22): 252-260.

[24]牟萍, 杨胜发, 童思陈. 基于Morlet小波分析的嘉陵江流域年径流周期研究. 重庆交通大学学报: 自然科学版, 2016, 35(1): 76-79, 171-171.

[25]李二辉, 穆兴民, 赵广举. 1919—2010年黄河上中游区径流量变化分析. 水科学进展, 2014, 25(2): 155-163.

[26]高迎春, 姚治君, 刘宝勤, 吕爱锋. 密云水库入库径流变化趋势及动因分析. 地理科学进展, 2002, 21(6): 546-553.

[27]李子君, 李秀彬. 水利水保措施对潮河流域年径流量的影响——基于经验统计模型的评估. 地理学报, 2008, 63(9): 958-968.

[28]王静怡, 王晓燕. 密云水库流域径流变化特征及影响因素分析. 首都师范大学学报: 自然科学版, 2007, 28(2): 89-92, 97-97.

[29]王巧平, 王成建. 海河流域人类活动对径流的影响分析. 海河水利, 2009, (1): 4-6.

[30]李屹峰, 罗跃初, 刘纲, 欧阳志云, 郑华. 土地利用变化对生态系统服务功能的影响——以密云水库流域为例. 生态学报, 2013, 33(3): 726-736.

[31]高训宇, 易忠, 贾东民, 郝丽娟. 水务普查成果在密云水库应用分析. 北京水务, 2013, (5): 40-42.