基于蒙特卡洛法的井壁稳定可靠度随机变量敏感性分析

胜亚楠 管志川 罗鸣 李文拓 巨然

1.中国石油大学（华东）石油工程学院；2.中海石油（中国）有限公司湛江分公司

油气井工程是一项隐蔽的地下工程，存在着大量的随机性、模糊性和不确定性，是一项高风险作业，其中，井壁稳定性失效是钻井工程中主要的复杂情况与事故之一［1-3］。地层坍塌及破裂压力是保持井壁稳定的安全钻井液密度窗口的上下限，由于地质环境的复杂性，测井及地震解释资料的不完备性以及分析模型的区域适用性等，都会导致地层坍塌及破裂压力计算结果存在着不确定性［4-5］，基于不确定性的预测结果进行钻井设计，会导致不可预知的风险。在实际井壁稳定性分析中，对于已钻井来说，可以通过各种测井资料，具备条件时还可以利用岩心室内实验数据，获取计算模型中所需要的各种岩石力学参数和地应力结果；对于新井而言，如果是开发井，由于具有了较多相同或者相似构造、区块上的邻井，虽然本井的各项岩石参数无法获取，但是可以根据多口邻井的测井及岩心实验数据来估计［6］；如果是探井，由于可参考的邻井资料较少甚至缺乏，那么对于新井坍塌及破裂压力的预测就存有较大的不确定性。因此，对坍塌及破裂压力的计算模型进行不确定性方面的分析，获取计算模型中最为敏感的因素，从而有助于通过一定的方法和手段提高敏感因素的准确程度，而对于那些不敏感因素，则可以根据井眼或者已钻井的统计数据估计其范围，最终减少坍塌及破裂压力预测结果的不确定范围，提高井壁稳定可靠度。

1 井壁稳定性可靠度随机变量敏感性分析

1.1 蒙特卡洛模拟

本文基于Monte-Carlo随机模拟方法进行井壁稳定性可靠度随机变量敏感性分析。Monte-Carlo方法是求解工程技术问题近似解的数值计算方法［7-9］，以统计抽样理论为基础，利用随机数进行抽样实验或随机模拟，通过对有关的随机变量进行统计，以求得统计特征值作为待解问题的数值解。具体求解步骤如下：

（1）结合地质力学参数的概率分布，运用蒙特卡洛模拟方法，将模拟次数设定为4 000，生成4 000个符合地质力学参数概率分布特征的随机数，并代入地层坍塌压力和地层破裂压力计算模型中，得到4000个计算结果；

（2）统计分析计算结果，并基于正态信息扩散原理，分别得到不同地质力学参数概率分布下的坍塌压力和破裂压力的概率分布，得到其均值、方差及变异系数；

（3）通过对比分析不同地质力学参数概率分布下得到的坍塌压力和破裂压力概率分布的变异系数，讨论井壁稳定性可靠度随机变量的敏感性。

1.2 井壁稳定分析模型

处于地层深处的岩石受上覆地层压力、水平方向地应力及地层孔隙压力的作用，钻开井眼之前，地下岩石处于应力平衡状态；井眼钻开以后，井内钻井液液柱压力取代了所钻岩层原先对井壁的支撑作用，破坏了地层的原有应力平衡，引起井眼周围应力重新分布，导致井壁不稳定。井壁失稳主要有2种表现形式［10］：井壁的剪切坍塌（井壁坍塌）和井壁的张性破裂（井漏）。从力学的角度分析，造成井壁坍塌的主要原因是由于井内液柱压力太低，使得井壁周围岩石所受应力超过岩石本身的强度而产生剪切破坏。井漏是一种在钻井过程中钻井液或其他工作流体漏失到地层中的现象。当井筒内钻井液液柱压力较小时，井壁周围岩石所受到的周向应力为压应力，随着井筒内钻井液液柱压力的增大，井壁周围岩石周向应力变小，当钻井液液柱压力增至一定程度，岩石周向应力将变为负值，也就是岩石所受到的周向应力由压缩变为拉伸，当这种拉伸大到足以克服岩石的抗拉强度时，地层即产生破裂造成井漏。

目前较为常用的地层坍塌压力计算模型假定地层渗透率非常小，且钻井液性能优良，基本上与地层不发生渗透流动，根据Mohr-Coulomb强度准则，其坍塌压力计算公式为［11］

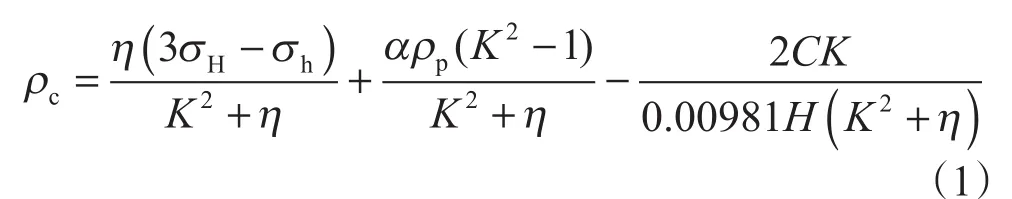
式中，ρc为坍塌压力，用当量钻井液密度表示，g/cm3；H为 井 深，m；K=cot（45°-ϕ/2），ϕ为 岩 石 内 摩 擦角，°；C为岩石的黏聚力，MPa；ρp为地层孔隙压力，用当量钻井液密度表示，g/cm3；σH为最大水平主应力，用当量钻井液密度表示，g/cm3；σh为最小水平主应力，用当量钻井液密度表示，g/cm3；η为应力非线性修正系数，无量纲，文中取0.95；α为有效应力系数，无量纲，文中取0.8。

Mohr-Coulomb强度准则没有考虑中间主应力的影响，在工程上一般采用Drucker-Prager强度准则，则坍塌压力的计算公式还可以表达为

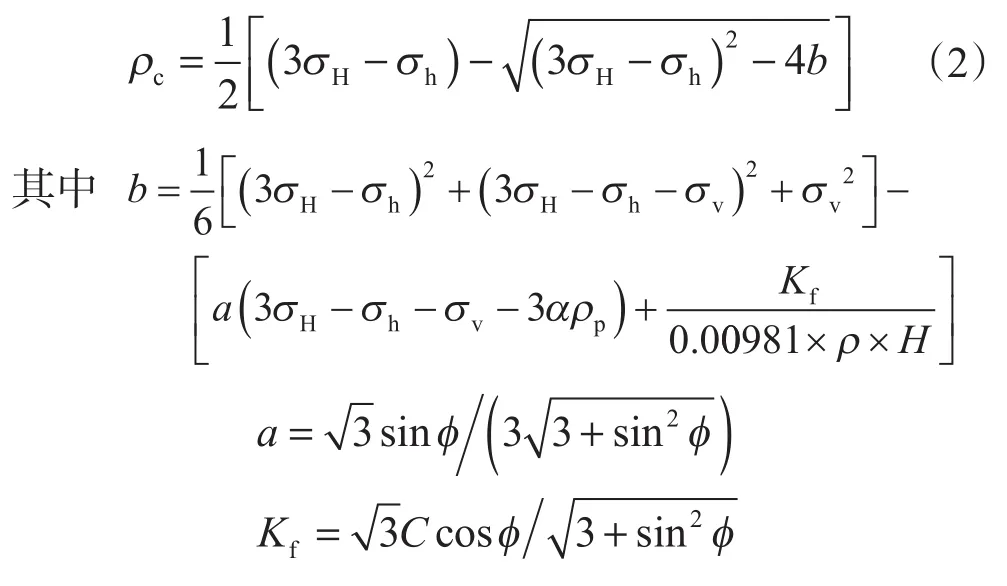
地层破裂压力是由于井内钻井液密度过大使井壁岩石所受的周向应力超过岩石的拉伸强度而造成的。目前较为常用的地层破裂压力计算公式为［12］

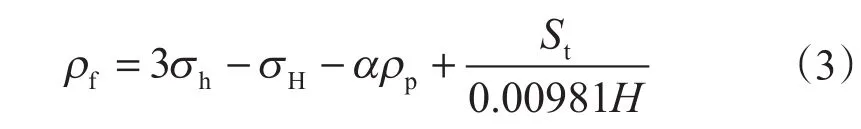
式中，ρf为地层破裂压力，用当量钻井液密度表示，g/cm3；St为岩石抗拉强度，MPa。

通过分析，将井壁稳定性计算模型中的参数划分为3类：井眼轨迹参数、原始地应力和岩石力学参数。其中，井眼轨迹可以根据钻井设计或者MWD数据准确获得；原始地应力和岩石力学参数，通常是根据测井或地震解释资料，通过间接数学模型计算获得，因此存在大量的不确定性，这些地质力学参数也是进行敏感性分析的重点考虑的参数。根据井壁稳定性计算公式可知，需要进行敏感性分析的参数有：地层孔隙压力、最大水平主应力、最小水平主应力、垂直向力、岩石内摩擦角、岩石内聚力和岩石抗拉强度。

地质力学参数的概率分布特征参数见表1。

表1 计算模型各参数分布形式及分布参数Table 1 Distribμtion pattern of each parameter in the compμtation model and distribμtion parameters

根据表中各参数设定的概率分布，基于蒙特卡洛模拟，随机生成4 000个符合概率分布特征的随机数，代入公式（1）～（3）计算地层坍塌压力及破裂压力。为考虑不同地应力场下参数的敏感性，表1分别对应3种不同原始地应力场情况，即：垂向应力为最大主应力（σv＞σH＞σh）、垂向应力为中间主应力（σH＞σv＞σh）和垂向应力为最小主应力（σH＞σh＞σv）。其中，井深为 1 000 m。

2 结果分析与讨论

通过蒙特卡洛模拟，分别得到不同地质力学参数概率分布下的坍塌压力和破裂压力的概率分布，得到其均值、标准差及变异系数，结果如表2所示。变异系数越大，表示该地质力学参数对破裂或坍塌压力计算结果的影响越大。

2.1 不同应力场条件下的敏感性

不同地应力场条件下地质力学参数对坍塌和破裂压力影响的敏感性分析结果如图1所示。

2.1.1 垂向应力为最大主应力 从图1可以看出，不同地质力学参数对地层破裂压力（FMW）影响敏感性依次为：最小水平地应力＞最大水平地应力＞孔隙压力＞岩石抗拉强度；不同地质力学参数对基于 Drucker-Prager准则的坍塌压力（CMW（D-P））影响敏感性依次为：孔隙压力＞内摩擦角＞内聚力＞垂直主应力＞最大水平地应力＞最小水平地应力；不同地质力学参数对基于Mohr-Coulomb准则的坍塌压力（CMW（M-C））影响敏感性依次为：最大水平地应力＞孔隙压力＞内聚力＞内摩擦角＞最小水平地应力。

表2 不同地质力学参数概率分布下的坍塌和破裂压力概率分布结果Table 2 Probabilistic distribution results of collapse and fracture pressures for the probabilistic distribution of different geomechanical parameters

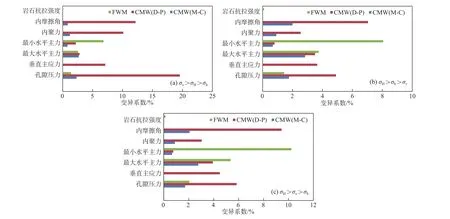
图1 不同地应力场条件下基于不同地质力学参数得到的坍塌和破裂压力计算结果的变异系数Fig.1 Variation coefficient of collapse and fracture pressures calculated based on different geomechanical parameters in different ground stress fields

2.1.2 垂向应力为最小主应力 从图1中可以看出，不同地质力学参数对地层破裂压力（FMW）影响敏感性依次为：最小水平地应力＞最大水平地应力＞孔隙压力＞岩石抗拉强度；不同地质力学参数对基于 Drucker-Prager准则的坍塌压力（CMW（D-P））影响敏感性依次为：内摩擦角＞孔隙压力＞垂直主应力＞最大水平地应力＞内聚力＞最小水平地应力；不同地质力学参数对基于Mohr-Coulomb准则的坍塌压力（CMW（M-C））影响敏感性依次为：最大水平地应力＞内摩擦角＞孔隙压力＞内聚力＞最小水平地应力。

2.1.3 垂向应力为中间主应力 从图1中可以看出，不同地质力学参数对地层破裂压力（FMW）影响敏感性依次为：最小水平地应力＞最大水平地应力＞孔隙压力＞岩石抗拉强度；不同地质力学参数对基于 Drucker-Prager准则的坍塌压力（CMW（D-P））影响敏感性依次为：内摩擦角＞孔隙压力＞垂直主应力＞最大水平地应力＞内聚力＞最小水平地应力；不同地质力学参数对基于Mohr-Coulomb准则的坍塌压力（CMW（M-C））影响敏感性依次为：最大水平地应力＞内摩擦角＞孔隙压力＞内聚力＞最小水平地应力。

2.2 不同破坏准则下的敏感性

不同破坏准则下地质力学参数对坍塌和破裂压力影响的敏感性分析结果如图2所示。

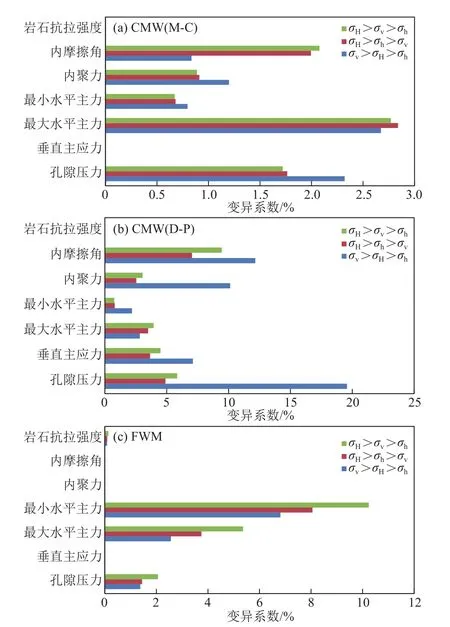
图2 不同破坏准则下基于不同地质力学参数得到的坍塌和破裂压力计算结果的变异系数Fig.2 Variation coefficient of collapse and fracture pressures calculated based on different geomechanical parameters under different failure criteria

2.2.1 基于Mohr-Coulomb准则的坍塌压力（CMW（M-C）） 从图2中可以看出，垂向应力为最大主应力应力场下（σv＞σH＞σh），不同地质力学参数对基于Mohr-Coulomb准则的坍塌压力（CMW（M-C））影响因素敏感性：最大水平地应力＞孔隙压力＞内聚力＞内摩擦角＞最小水平地应力；垂向应力为中间主应力应力场（σH＞σv＞σh）下，影响因素敏感性：最大水平地应力＞内摩擦角＞孔隙压力＞内聚力＞最小水平地应力；垂向应力为最小主应力应力场（σH＞σh＞σv）下，影响因素敏感性：最大水平地应力＞内摩擦角＞孔隙压力＞内聚力＞最小水平地应力。

2.2.2 基于Drucker-Prager准则的坍塌压力（CMW（D-P）） 从图2中可以看出，垂向应力为最大主应力应力场下（σv＞σH＞σh），不同地质力学参数对基于Drucker-Prager准则的坍塌压力（CMW（D-P））影响因素敏感性：孔隙压力＞内摩擦角＞内聚力＞垂直主应力＞最大水平地应力＞最小水平地应力；垂向应力为中间主应力应力场（σH＞σv＞σh）下，影响因素敏感性：内摩擦角＞孔隙压力＞垂直主应力＞最大水平地应力＞内聚力＞最小水平地应力；垂向应力为最小主应力应力场（σH＞σh＞σv）下，影响因素敏感性：内摩擦角＞孔隙压力＞垂直主应力＞最大水平地应力＞内聚力＞最小水平地应力。

2.2.3 地层破裂压力（FWM） 从图2中可以看出，垂向应力为最大主应力应力场下（σv＞σH＞σh），不同地质力学参数对地层破裂压力（FMW）影响因素敏感性：最小水平地应力＞最大水平地应力＞孔隙压力＞岩石抗拉强度；垂向应力为中间主应力应力场（σH＞σv＞σh）下，影响因素敏感性：最小水平地应力＞最大水平地应力＞孔隙压力＞岩石抗拉强度；垂向应力为最小主应力应力场（σH＞σh＞σv）下，影响因素敏感性：最小水平地应力＞最大水平地应力＞孔隙压力＞岩石抗拉强度。

3 结论与建议

（1）基于蒙特卡洛模拟分析了与井壁稳定可靠度相关的随机变量的敏感性。进行敏感性分析的参数包括：地层孔隙压力、最大水平主应力、最小水平主应力、垂直向力、岩石内摩擦角、岩石内聚力、和岩石抗拉强度。同时，不同应力场以及不同破坏准则情况下参数的敏感性在本文中也被讨论。

（2）基于Mohr-Coulomb准则的坍塌压力（CMW（M-C））：无论处于哪种地应力场，最为敏感的影响因素都是最大水平地应力；基于Drucker-Prager准则的坍塌压力（CMW（D-P））：当向应力为最大主应力时，最为敏感的影响因素是孔隙压力；垂向应力为中间主应力时，最为敏感的影响因素是内摩擦角；垂向应力为最小主应力时，最为敏感的影响因素是内摩擦角。地层破裂压力（FMW）：无论处于哪种地应力场，最为敏感的影响因素均为最小水平地应力。

（3）通过研究获取了不同应力场和破坏准则下井壁稳定性计算模型中最为敏感的因素，从而有助通过采取一定的措施提高敏感因素的准确程度，而对于那些不敏感因素，则可以根据井眼或者已钻井的统计数据估计其范围，最终减少坍塌及破裂压力预测结果的不确定性，提高井壁稳定的可靠度。

参考文献：

［1］陈庭根，管志川.钻井工程理论与技术［M］.东营：石油大学出版社，2000：51-54.CHEN Tinggen, GUAN Zhichuan.Theory and technology of drilling engineering ［M］.Dongying: Petroleum University Press, 2000: 51-54.

［2］蒋希文.钻井事故与复杂问题［M］.第2版.北京：石油工业出版社，2006：72-80.JIANG Xiwen.Drilling accidents and complex problems［M］.2nd Edition.Beijing: Petroleum Industry Press,2006: 72-80.

［3］OTTESEN S, ZHENG R H, MCCANN R C.Borehole stability assessment using quantitative risk analysis［R］.SPE 52864, 1999.

［4］柯珂，管志川，周行.深水探井钻前含可信度的地层孔隙压力确立方法［J］.中国石油大学学报（自然科学版），2009，33（5）：61-67.KE Ke, GUAN Zhichuan, ZHOU Hang.An approach to determining pre-drilling formation pore pressure with credibility for deep-water exploration well ［J］.Journal of China University of Petroleum （Natural Science Edition）, 2009, 33（5）: 61-67.

［5］MOSTAFAVI V, AADNOY B S, HARELAND G.Model based uncertainty assessment of wellbore stability analyses and downhole pressure estimations ［R］.American Rock Mechanics Association, 2011.

［6］黄荣樽，庄锦江.一种新的地层破裂压力预测方法［J］.石油钻采工艺，1986，10（3）：1-14.HUANG Rongzun, ZHUANG Jinjiang.A new method for predicting formation fracture pressure ［J］.Oil Drilling& Production Technology, 1986, 10（3）: 1-14.

［7］宫凤强，侯尚骞，岩小明.基于正态信息扩散原理的Mohr-Coulomb强度准则参数概率模型推断方法［J］.岩石力学与工程学报，2013，13（11）：2225-2234.GONG Fengqiang, HOU Shangqian, YAN Xiaoming.Probability model deduction method of Mohr-Coulomb criteria parameters based on normal information diffusion principle ［J］.Chinese Journal of Rock Mechanics and Engineering, 2013, 13（11）: 2225-2234.

［8］LI G, BAI M.Parametric sensitivity investigation: analysis of wellbore stability ［R］.International Society for Rock Mechanics and Rock Enginecring, 2011.

［9］UDEGBUNAM J E, AADNOY B S, FJELDE K K.Uncertainty evaluation of wellbore stability model predictions ［J］.Journal of Petroleum Science &Engineering, 2014, 24（5）: 254-263.

［10］PAYTEN W, LAW M.Estimating the plastic collapse of pressure vessels using plasticity contours ［J］.International Journal of Pressure Vessels & Piping, 1998,75（7）: 529-536.

［11］陈勉，金衍，张广清.石油工程岩石力学［M］.北京：科学出版社，2008：45-53.CHEN Mian, JIN Yan, ZHANG Guangqing.Rock mechanics in petroleum engineering ［M］.Beijing:Science Press, 2008: 45-53.

［12］葛洪魁，王爱国.修正Holbrook地层破裂压力预测模型［J］.石油钻探技术，2001，29（3）：20-22.GE Hongkui, WANG Aiguo.Modification of Holbrook’s fracture pressure prediction model ［J］.Petroleum Drilling Technology, 2001, 29（3）: 20-22.