断层作用下管道受压时数值模型适用性分析
,
(中国石油大学(北京) 机械与储运工程学院 北京 102249)
0 引 言
随着我国管网的快速发展,大输量、大管径、高压长输油气管道也在不断修建。经验表明,地质灾害引发的地面移动所产生的永久地面变形是长输管道的主要威胁,如地震带的断层错动,液化而导致的土壤侧向扩展,地震或其他原因导致的滑坡,土壤的沉陷等[1]。其中,断层位移形式最为危险,断层运动时将产生较大的地面位移,使得管道内部产生较大的拉压应变,从而产生拉裂或屈曲失效,通常采用基于应变的方法进行抗震设计校核[2-5]。1971年美国San Fernando地震、1972年马那瓜地震、1976年唐山地震以及1999年台湾集集地震等,无疑都对管线造成了巨大的损坏。
近年来,国内外学者对管道跨越断层时的数值模拟应变分析做了大量的研究,如2001年Takada[6]提出了一种梁壳耦合模型,使用壳单元模拟管道的大变形段,用梁单元模拟远端管道;2004年,刘爱文等[7]提出一种含有等效边界的有限元模型,使用土弹簧模拟土壤对管道的约束作用,并推导得到了半无限埋地管道端部受拉时的轴力与位移定量关系,以非线性弹簧的形式施加到壳单元模型两侧替代远端管道的影响,在保证精度的同时大大降低了计算时间;2005年,刘学杰等[8]提出一种管单元-弯管单元模型,采用弯管单元模拟断层附近管道,管单元模拟远端管道,土弹簧模拟土壤作用。弯管单元能够准确描述管道发生局部屈曲前的截面椭圆化过程,计算效率高,适用于工程设计;2008年LiuMing[9]等提出了一种使用土弹簧模拟管土相互作用的梁壳耦合模型,Xie等[10]基于数值模型,对断层作用下高密度聚乙烯(HDPE)管道的失效进行了全面分析。建立了基于土弹簧的管单元和壳单元模型,还建立了基于实体模拟土壤,接触模拟管土作用的三维实体模型,通过对比3种模型与离心机实验结果发现,3种模型均能较好地预测管道在断层作用下的应变结果,最终基于实体模型分析了HDPE管道的屈曲特征;2015年郑伟,张宏[11]等人对比了断层作用下管道受拉应变时计算的多种模型。
土壤发生断层的类型有很多,包括走滑断层、正逆断层等,不同断层下管道的受力不同,造成的危害也各异,工程中管道受压的情况更为常见,且管道的承压能力远小于其抗拉能力,但却没有关于管道受压时有限元模型的对比。本文在郑伟等人的研究基础上,基于有限元软件平台ABAQUS建立了管道穿越走滑断层、逆断层时的多种有限元模型,考虑了多个参数,多种工况,分别比较了各个模型计算结果的优缺点,并给出了各个模型的适用范围,工程中可供参考。
1 断层工况分析
根据断层时土壤的相对移动情况可将断层分为正断层、逆断层和走滑断层,正断层是指断层上盘相对于下盘向下移动。相反,逆断层是指断层上盘相对于下盘向上移动。走滑断层是指断层的两盘沿着断面走向做相对移动,它是在地壳不均匀挤压作用或水平剪切作用下形成的。如图1所示。
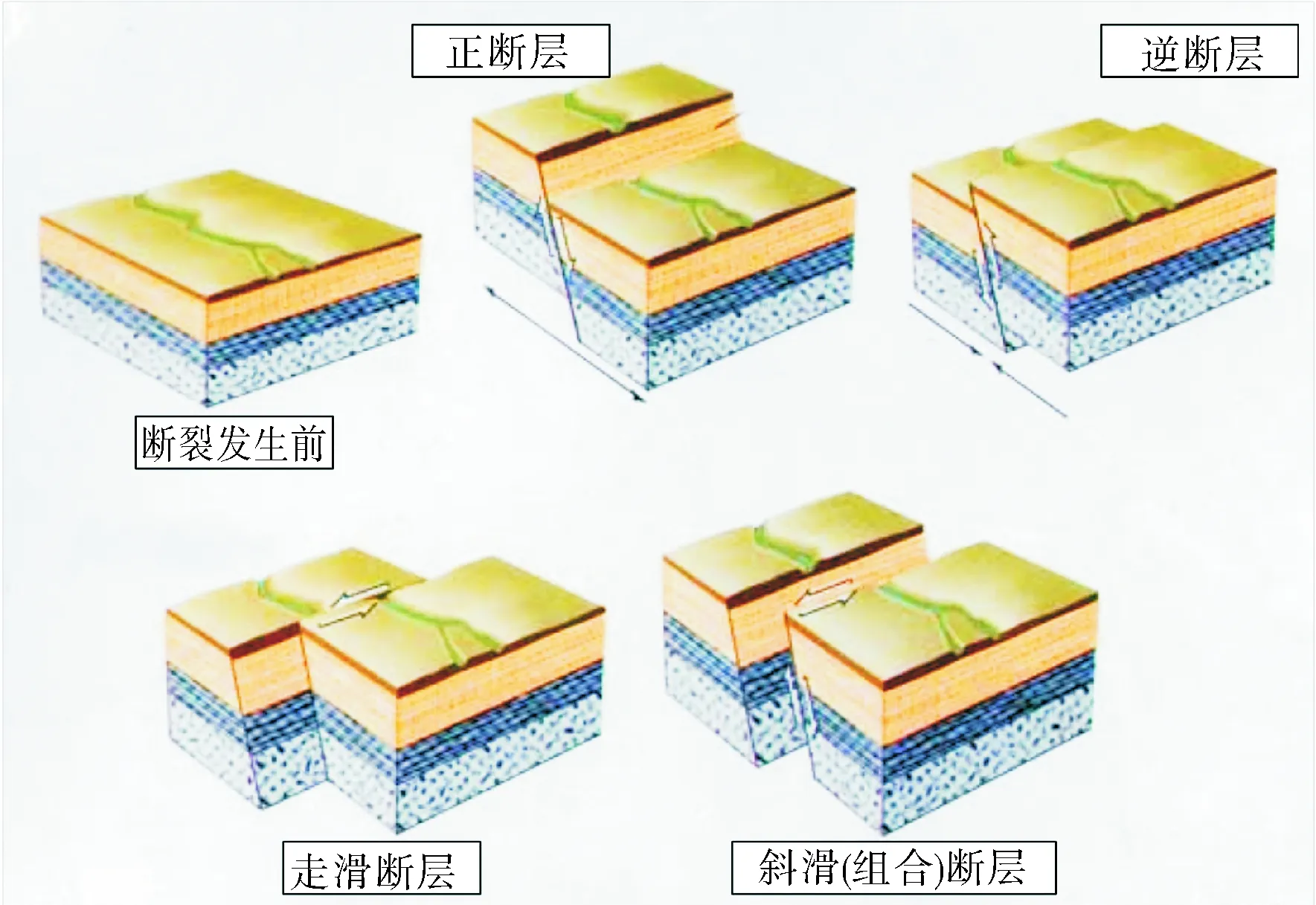
图1 断层类形示意图
埋地管道穿越断层时,会在断层位移作用下发生变形,使得管道承受较大荷载而失效。管道受力形式根据断层的类型也各异,本文只讨论管道整体受压的情况。当埋地管道穿越逆断层时,由于管土之间的摩擦作用以及管道之间的压应力,会使管道随着断层上盘向上运动而发生大变形,在断层处由于受力过大可能发生塑性形变或局部屈曲现象;埋地管道穿越走滑断层,当管道与断层的交角处于90~180°时,管道跟随断层两盘发生相对位移,连续管道之间产生挤压作用,并且受到管土之间的摩擦力,使得管道受压,当断层作用较大时,管道可能发生局部屈曲或塑性形变。
2 数值模型
2.1 管土相互作用模型
通常情况下,由于断层的位错量较大,管道和土壤的变形已经进入非线性状态,本文采用ALA《Guideline for the Design of Buried Steel Pipeline》提出的采用非线性的3个方向上的土弹簧来模拟管土之间的作用,其中包括轴向土弹簧KT和横向土弹簧(包括水平向KP和竖直向KQ),作用方式如图2所示,Tu,Pu,Qu和Qd分别为侧向、轴向与垂直向上与垂直向下土弹簧极限抗力,Δp,Δt, Δqu, 和Δqd分别为对应屈服位移。可以得到,在管道侧向与轴向,土弹簧呈现对称性,而由于一般埋地较浅,管道地基深度远大于管道埋深,所以在管道垂直向上土弹簧极限抗力Qu远小于垂直向下土弹簧极限抗力Qd,如图2所示。具体参数可从规范ALA中获得。在ABAQUS中选用已有的JOINTC单元模拟土弹簧,JOINTC单元可以描述两个节点相对位移所产生的应力。

图2 土弹簧作用示意图
2.2 管道模型
随着计算机科学技术的发展,学者们提出了多种基于有限元模型的数值分析方法。本文选取了管单元模型、梁壳耦合模型、固定边界壳单元模型以及等效弹簧边界模型进行对比分析。
1)管单元模型
模型采用PIPE31单元模拟管道,JOINTC单元模拟土弹簧;由于断层两侧应力较大,作为研究的重点,建模时在断层两端各100 m范围内管道每隔0.1 m划分一个单元,选用较密单元能更准确地描述管道变形,在加密段两侧各1 000 m内每隔1 m划分一个单元,用来描述管道远端行为。模型如图3(A)所示。
2)梁壳耦合模型
穿越断层附近100 m内的管道采用壳单元建模,因为壳模型更接近于管道作为一个中空圆柱形薄壳的真实结构, 因而它能够更好地分析像管道屈曲这样的大变形情况。管道环向划分成24个单元,轴向0.4 m长度一个单元;两端采用简化模型,减少计算,使用管单元建模,长度分别取1 000 m。壳单元管道两端与管单元管道耦合,将管单元与壳连接一侧作为控制点,对壳单元管道端部进行全约束,此区域的各节点之间不会发生相对位移,只会随着控制点做刚性运动,即将管端行为传递给壳单元管道边界,从而减少了单元的数量进而减小计算成本。模型如图3(B)所示。
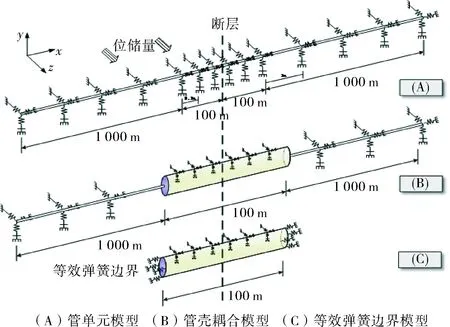
图3 管道有限元模型
3)固定边界单元模型
模型中只有采用壳单元模拟的管道,为消除边界对断层受力的影响,管道分析长度取2 000 m;管道环向划分成24个单元,管道沿轴向每隔0.4 m长度划分为一个单元;以JOINTC单元连接模拟三个方向土弹簧。
4)等效弹簧边界模型
2004年刘爱文提出了等效边界模型,在壳单元两端以非线性弹簧的形式来模拟端部作用,代替离断层较远处直线段管道的变形影响。模型如图3(C)所示,壳单元管道模型长度取100 m,环向划分为24个单元,轴向每0.4 m长度划分一个单元;两端连接24个弹簧单元用以描述等效弹簧。本文采用刘爱文提出的等效弹簧应力计算公式:
(1)
式中:F为等效弹簧外力,fs为轴向单位长度管道受到的摩擦力,ΔL为管道伸长量,A为管道截面面积,E为弹性模量。公式假设远端管道处于弹性状态,管道只受滑动摩擦力,不受静摩擦力影响。
3 结果分析对比
3.1 工况参数
3.1.1管材参数
本文采用Ramberg-Osgood模型来描述管材的弹塑性模型。该管材模型能较好的描述管道的应力应变关系,表达式如式(2):
(2)
式(2)中,E为管材的初始弹性模量;ε为应变;σ为应力;σs为管材的屈服应力;α和N为R-O模型参数。
本文选用西气东输二线断层区X80HD2管道的基本参数,管道外径1 219 mm,壁厚22 mm,Ramberg-Osgood模型参数中α=15.94,N=15.95[12]。
3.1.2土弹簧参数
断层区管道敷设管沟采用砂土回填,砂土内摩擦角度35°,管土摩擦系数0.6,土壤容重18 kN/m3;管道管径1 219 mm,埋深2.1 m。根据规范ALA《Guideline for the design of buried steel pipeline》中公式计算得到土弹簧参数如表1所示。

表1 土弹簧参数
3.1.3断层参数
1)走滑断层
为了保证结果的可靠性,取多组数值进行计算。管道与断层交角β分别取90、110、130和150°,断层位错量分别取0.15、0.3、0.45、0.6、0.75、0.9、1.05、1.2、1.35和1.5 m。
2)逆断层
同样为了确保结果的准确性,取多组数值。管道与断层倾角α分别取45、60和75°,断层位错量分别取0.15、0.3、0.45、0.6、0.75、0.9、1.05、1.2、1.35和1.5 m。
3.2 走滑断层结果分析
利用四种有限元模型对多种走滑情况的计算,结果如图4所示,由结果可知,对不同工况下管道轴向最大应变的计算,四种模型得到的结果较为吻合;当管道与断层交角大于90°时,管单元模型在计算轴向最小应变的值偏小;在断层位错量小于1.35 m时,梁壳耦合模型和等效弹簧边界模型计算轴向最小应变时的结果与壳单元模型基本吻合,在断层位错量大于1.35 m时,梁壳耦合模型和等效弹簧边界模型都与固定边界的壳单元模型存在较小的偏差。
3.3 逆断层结果分析
本文以管道在断层两侧各50 m内的轴向最大最小应变作为计算结果,结果如图5所示,由结果可知,梁壳耦合模型与等效弹簧边界模型在计算轴向最大或最小应变时的结果都与固定边界壳单元模型结果相吻合;当管道与断层相交角大于45°,断层位错量大于1 m时,管单元模型在计算轴向最大应变时的结果较其余模型结果有较小的偏差;而当断层位错量大于0.6 m时,管单元的计算结果较其余模型结果偏大,并且偏差随着断层位错量的增加而显著增加。

图4 不同算例下管道轴向应变结果对比

图5 不同算例下管道轴向应变结果对比
3.4 模型计算效率
ABAQUS中的计算,都是通过对模型建立的刚度矩阵进行计算,进而分析得到结果[13]。在分析管道穿越断层时的受力,通常采用壳单元模型计算得到的结果较为准确,但是由于壳单元模型单元数量较多,计算时间较长。在保持一定计算精度的基础上,常采用梁壳或等效边界模型简化,减少单元数量,降低计算成本。本文在同一计算机上进行各模型间的计算,得到各模型完成分析计算的时间,结果如图6所示,由图可知,壳单元的计算时间最长,梁壳耦合及等效边界模型的计算时间大大减少,管单元计算时间最短,计算效率最高。但是由前文分析可知,在部分工况下,管单元结果存在一些偏差。

图6 不同模型平均计算时间对比
4 结 论
管道在油气输送系统中的作用不可或缺,其在穿越断层时的受力分析非常有意义,本文研究了管道在穿越断层时受压的情况,在此基础上进行了对管单元、梁壳耦合、等效边界以及固定边界壳单元这四种常用有限元分析模型计算结果的分析比较,得到如下结论:
1)通过对走滑断层以及逆断层的分析可以看出,对于管道轴向最大应变的计算,四种模型得到的结果都相吻合,但从计算效率的比较中可以看到,管单元模型所用的时间最短,更为经济,可以进行大批量计算,在工程中具有较广的适用性。
2)对于管道轴向最小应变的计算,从结果的对比分析中可以看出,管单元的结果存在较大的偏差;而基于壳单元、梁壳耦合及等效边界模型在分析逆断层时得到的结果吻合较好,在分析走滑断层时,若断层位错量过大,梁壳耦合等效边界模型都存在偏差,使用壳单元得到的结果更为保守。由计算效率的比较可以看出,采用梁壳耦合模型及等效边界模型计算的时间较壳单元模型相比大大减少,因此在位错量较小时,建议使用上述两个模型。
[1] 刘啸奔, 张宏, 李勐,等. 断层作用下埋地管道应变分析方法研究进展[J].油气储运,35(8): 799-807.
[2] Canadian Standards Association. Oil and Gas Pipeline Systems :CSA-Z662 [S]. 2007.
[3] American lifelines alliance. Guideline for the design of buried steel pipeline[S]. 2001.
[4] 国家质量监督检验总局.油气输送管道线路工程抗震技术规范:GB-50470 [S].北京: 中国计划出版社, 2008.
[5] 张宏,崔红升.基于应变的管道强度设计方法的适用性[J]. 油气储运, 2012, 31(12):952-954.
[6] SHIRO T,NEMAT H,KATSUMI F.A new proposal for simplified design of buried steel pipes crossing active faults[J].Earthquake Engineering & Structural Dynamics,2001,30(8):1243-1257.
[7] 刘爱文,胡聿贤,赵凤新,等.地震断层作用下埋地管线壳有限元分析的等效边界方法[J].地震学报, 2004, 26(S1):141-147.
[8] 刘学杰,孙绍平.地下管道穿越断层的应变设计方法[J].特种结构, 2005, 22(2):81-85.
[9] LIU M,WANG Y Y,YU Z. Response of pipelines under fault crossing[C].Vancouver:Proceedings,international offshore and polar engineering conference,2008,47(S1):260-260.
[10] XIE X J. Numerical analysis and evaluation of buried pipeline response to earthquake-induced ground fault rupture[D]. Troy:Rensselaer Polytechnic Institute,2008:6-36.
[11] 郑伟, 张宏, 刘啸奔,等. 断层作用下管道应变计算有限元模型对比研究[J]. 石油机械, 43(12): 109-113.
[12] 中国石油管道建设项目经理部. 西气东输二线管道工程强震区和活动断层区段埋地管道基于应变设计导则:Q/SY GJX 0136 [S]. 北京:石油工业出版社,2008.
[13] ABAQUS Inc.Abaqus analysis user′s manual Volume IV: Element[M]. ABAQUS Inc. 2004.

