基于非线性预处理及逻辑回归的异常检测算法

董　伟，杨　晨，邵俊杰

(中国电子信息产业集团有限公司第六研究所工业控制系统信息安全技术国家工程实验室，北京 102209)

0　引言

随着互联网的爆炸式发展，网络安全已上升到国家战略层面，面对日益复杂的网络环境，传统的协议识别技术已不再适用。2015年微软在Kaggle上发起了一个恶意代码分类的比赛，而取得第一名的队伍的三名队员都不是安全出身，所采用的方法与常见的方法存在很大的不同，展现了机器学习在安全领域的巨大潜力[1]。特征工程作为机器学习领域极具分量的步骤，在工程中占用的时间远超我们的想象，特征工程的好坏直接关系到学习结果，可以说特征工程决定了模型的上限。

本文以数据挖掘及机器学习的视角去看待安全问题，在网络安全领域进行了初步实践。

1　数据预处理

1.1　实验数据集

KDD99数据集来源于美国国防部高级研究计划局(DARPA)的入侵检测评估项目，由 MIT Lincoln实验室进行数据集搜集，该项目始于1998 年，后经哥伦比亚大学的STOLFOS教授等人进行粗粒度数据处理后形成了一个新的数据集，该数据集用于1999年的KDD竞赛上，成为了著名的KDD99数据集。虽然年代有些久远，但KDD99数据集仍然是网络入侵检测领域的权威测试集[1]，为基于计算智能的网络入侵检测研究奠定基础。

KDD99数据集由41个特征以及1个类别标记组成，其中41个特征共分为4大类：TCP连接基本特征、TCP连接的内容的特征、基于时间的网络流量统计特征、基于主机的网络流量统计特征。类别标记分为两类：正常(normal)和异常(abnormal)，异常类型被分为4大类共39种攻击类型，其中22种攻击类型出现在训练集中，另有17种未知攻击类型出现在测试集中。

1.2　数据处理

KDD99数据集虽已经过粗粒度的处理，但仍然不能直接用于算法中。KDD99数据集数据属性按数据类型可分为两大类：离散属性(第2、3、4个特征)和连续属性。

由于KDD99中的离散属性都是标称属性，若直接将其映射为序数属性，则会大大增加调参工作量。为此，本文采用了独热编码(One-Hot Encoding)对数据进行处理，其方法是使用N位布尔变量来对N个状态进行编码，每个状态都由它独立的位表示，并有且仅有一位有效，其余N-1位全为0。独热编码的方式相比映射为序数属性的方式，不用增加调参的工作。对于线性模型来说，使用独热编码后可达到非线性的效果。而对于第三个属性，考虑其离散值较多，为避免引起“维数灾难”，将其舍弃。

图1　决策树模型

对于连续属性，一般而言，用较小的单位表示将导致该属性具有较大值域，因此趋向于使该属性拥有较大的“权重”，在基于距离的算法中，影响更甚。为了消去不同量纲对算法的影响，应对连续属性进行规范化处理。

常用的规范化方法有三种：最小—最大规范化、z分数规范化和按小数定标规范化。本文采用最小—最大规范化，其计算方法如公式所示:

(1)

1.3　属性子集选择

KDD99样本经数据预处理后由52维表示，这52个属性不仅会影响算法运行时间，而且可能会存在冗余属性，对实验结果造成干扰。为此一种方法是进行属性子集选择。常用的方法包括：逐步向前选择、逐步向后选择、逐步向前选择和逐步向后删除的组合以及决策树归纳[2]。本文采用决策树归纳的方法进行属性子集选择。

决策树算法最初是用来分类的，当决策树归纳用于属性子集选择时由给定的数据构造决策树，出现在树中的属性形成规约后的属性子集。

1.3.1评判指标

将数据标记为两类：正常(normal)和异常(abnormal)，用准确率(Precision)、召回率(Recall)、和F度量评估算法。准确率可以看作准确性的度量(即预测为正类的元组实际为正类所占的百分比)，召回率是完全性的度量(即正元组预测为正的百分比)，而F度量是准确率和回率的调和均值。这些度量计算公式如下:

(2)

(3)

(4)

其中，TP(True Positive)是指被分类器正确分类的正元组，FP(False Positive)是指被错误地标记为正元组的负元组，FN(False Negative)是指被错误地标记为负元组的正元组。

1.3.2实验结果分析

实验构建了基于信息熵的决策树模型，显示其前四层的树型表示如图1所示。

用图1中的特征子集表征数据，将“正常”元组标记为正类，采用10折交叉验证的方式，在决策树模型上进行分析，参照公式(2)、(3)、(4)的模型评判标准，其结果与用所有特征表征的数据运行结果对比如表1所示。

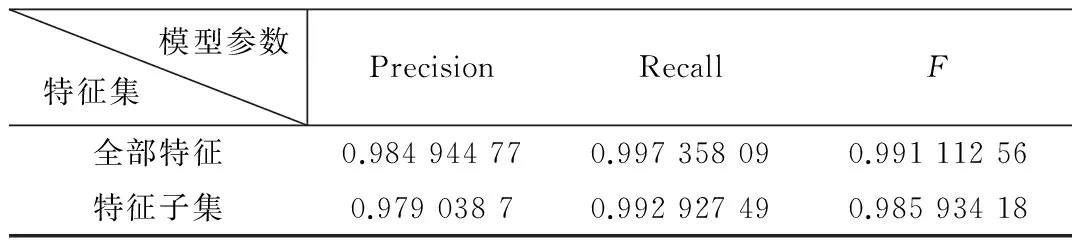
表1　数据对比表

如表1所示，采用所选特征子集对数据进行特征选择后，各度量值虽都略有所下降，但相差无几，故在后续研究中，选用上述特征子集进行运算分析，节约了时间成本。

2　算法设计及实现

2.1　回归分析

回归是研究自变量和因变量之间关系的一种预测模型技术。回归分析的目的是预测数值型的目标值，最直观的表现形式是依据输入构造目标值的计算公式，该公式就是回归方程(Regression Equation)，求解回归方程的回归系数的过程就是回归。回归分析包含多种预测模型，常见的有线性回归(Linear Regression)、逻辑回归(Logistic Regression)、多项式回归(Polynomial Regression)、逐步回归(Stepwise Regression)、岭回归(Ridge Regression)、套索回归(Lasso Regression)、回归(ElasticNet)等。

逻辑回归是比较常用的机器学习算法，原因在于它不但能指出自变量和因变量之间的显著关系，允许比较不同尺度的度量，还能快速地用较低的代价吸收新数据更新模型。因此，针对KDD99数据集数据类型复杂、特征维数较多的特点，选用逻辑回归算法来进行异常检测。

2.2　原理及设计

逻辑回归是一种广义线性回归，处理的是分类问题。线性回归的公式如下：

z=ω1x1+ω2x2+ω3x3+…+ωnxn+b=WTX+b

(5)

其中，XT=[x1x2x3…xn]是输入的样本特征，WT=[ω1ω2ω3…ωn]是方程的回归系数，b是常量。对于逻辑回归来说，其思想也是基于线性回归，但是回归公式并不是直接输出结果Z，而是增加激活函数，将方程的值域映射到某特定的取值空间(应根据目标值的要求选取适合的激活函数)，构造损失函数，求使损失函数最小的回归参数。

逻辑回归中单个样本的n维特征正向传播过程如图2所示。

图2　逻辑回归正向传播

单个样本的n维特征表现为正向传播的输入向量XT=[x1x2x3…xn]，回归系数是输入向量WT=[ω1ω2ω3…ωn]。由回归方程可知，此时无论迭代多少次，输出的z都是输入的线性映射，这是回归分析的一般结果，此时的回归模型只具有线性映射能力,而训练目标是识别数据集中的异常数据，属于二分类问题，因此必须加入激活函数将输出z映射到特定的值域，表示该数据标记为异常或正常数据的可能性。简而言之，激活函数(Activation Function)就是为算法提供非线性建模学习能力的，几种常见的激活函数如下，如图3所示。

图3　几种常见的激活函数

Sigmoid函数：

(6)

Tanh函数：

(7)

RuLU函数：

g(x)=max(0,x)

(8)

Sigmoid函数是使用范围最广的一类激活函数，具有指数函数的形状，由于它将输入映射到(0,1)之间，可以用来表示概率，因此将其用于异常检测输出结果用来表示数据异常或正常的概率。

损失函数是用来估量模型的预测值和真实值的不一致程度，这里用Loss(a,y)来表示，a表示预测类别，y表示真实类别。常用的损失函数有平方损失函数、log损失函数、指数损失函数等。

在Sigmoid激活函数的作用下:

标签取值的概率可表为:

P(y/x;ω)=(Gω(x))y(1-Gω(x))1-y

(9)

取似然函数为:

(10)

对数似然函数为:

(11)

取损失函数为:

(12)

(13)

其中，γ是学习率。

训练数据集的平均损失称为经验风险，为了防止过拟合，需要在经验风险的基础上加上表示模型复杂度的正则化项(regularization)或者罚项(penalty term)，在本算法中取正则项为平方损失，即参数的L2范数，此时模型的损失函数为：

(14)

其中，β为常量。

正则化后的梯度下降算法ω的更新过程变为：

(15)

综上所述，该方法的常规流程为，根据数据集及目标结果选择合适的训练模型，寻找预测函数(G(z))，构造损失函数，求使损失函数最小的模型参数，构造训练模型。

2.3　实现

本文的异常检测算法是基于KDD99数据集实现的，原始的训练数据集包含494 021条连接记录，测试数据集包含311 029条连接记录，每条连接记录的最后有一个标签来标明其类别信息，试验中将正常连接标记为1，异常连接标记为0。在对数据集进行非线性处理后，用训练数据集训练逻辑回归模型，效果如图4所示。

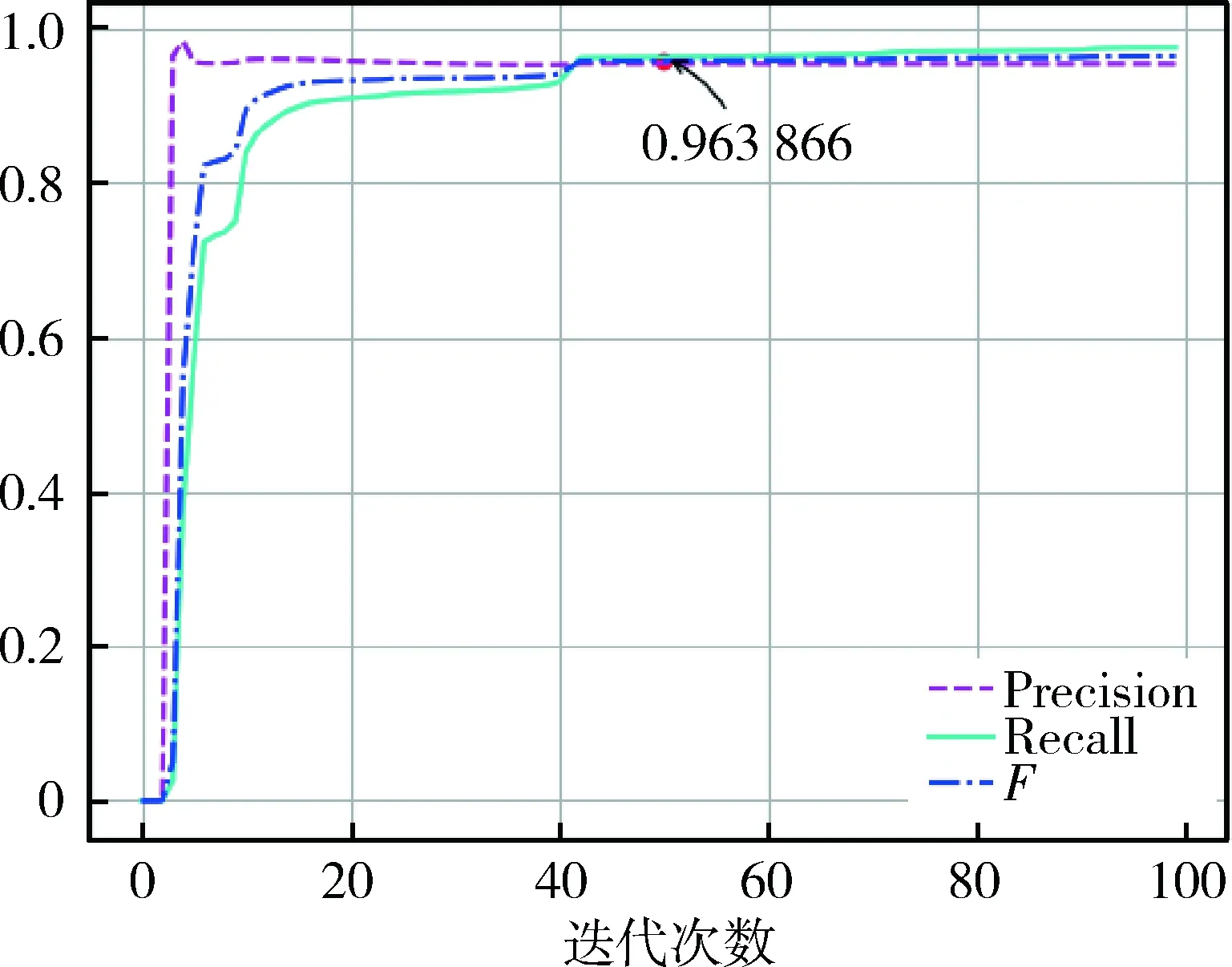
图4　逻辑回归模型评估

将算法迭代100次，并用每次迭代求出的回归系数测试待测数据集的回归程度，结果显示，在取学习率α=0.8时，模型在迭代45次左右后收敛。

将测试集带入模型，结果如图5所示。

图5　测试集预测结果

从图5中可以看出，随着迭代次数的增加，模型的准确率快速收敛，漏报率随有所增加，但未超过0.1%。

3　结果分析

试验中选用KDD99数据集，由于该数据集的每条记录都是以一次网络连接为单位，每条记录包含字符型、离散型和连续型数据，且各特征度量尺度不同，难以处理，因此选用非线性预处理的方式处理数据，将原始数据转化为可以直接输入逻辑回归模型学习的矩阵形式。实验结果表明，逻辑回归对测试集中的异常连接有较好的识别能力，但是随着迭代次数的增加，回归系数逐渐收敛，测试集的漏报率也有所增加，关于这一问题，未来还会进行针对性的研究来改进工作。

[1] 刘焱.Web全之机器学习入门[M].北京：机械工业出版社，2017.

[2] Han Jiawei, KAMBER M. Pei Jian.数据挖掘：概念与技术(第3版)[M]. 北京：机械工业出版社，2012.