城市轨道交通新站开通初期实时进出站客流量预测

姚恩建， 周文华， 张永生

(1.北京交通大学 城市交通复杂系统理论与技术教育部重点实验室，北京　100044；2.北京交通大学 交通运输学院，北京　100044)

随着城市轨道交通网络规模的持续扩大，客流时空分布规律愈加复杂，作为客流生成源头的进出站客流，运营管理部门需对其实时监测，准确把握未来短时间内客流变化趋势，从而实时调整运营计划，对突发大客流做出及时预警和响应。为此，高精度、小粒度的实时进出站客流量预测已成为精细化运营管理的关键。同时，新站不断开通运营，成为新线接入线网后实时客流预测的重点。然而，新站开通初期缺乏足够历史数据，且客流波动大，变化规律较不稳定，对未来短时间内客流的精准把握愈发艰难。因此，对新站开通初期实时进出站客流量预测方法的研究尤为必要。

针对城市轨道交通新站客流预测，目前国内外学者主要在项目可行性分析等过程中进行中长期或短期的客流需求预测，为新线开通后的客运组织等提供数据支撑。如光志瑞[1]基于车站可达性指标建立新线接入后新站进出站客流预测模型，得到新站开通后全天的进出站客流量，以评估新线开通后的运输组织方案。蔡昌俊[2]等基于非集计理论，预测了新线接入条件下的城市轨道交通新线车站与既有线车站之间的工作日客流量。程涛[3]等基于既有站客流规律采用多元线性回归模型预测新线开通初期的客运量，包括全天的客运强度及规模。赵路敏[4]等通过新线工程可行性研究报告的数据和既有路网OD数据预测新线开通后的全网客流。但是，以上研究均以日为单位预测新站客流，其预测粒度及精度尚不能满足城市轨道交通运营管理部门对客流实时监测的精细化运营需求。

对于实时客流预测方法，国内外已有诸多研究，常用模型包括时间序列模型[5-6]、卡尔曼滤波模型[7-8]、支持向量机模型[9-10]和神经网络模型[11-12]等。这些模型大多用显性的数学解析式或隐性的关系表达式描述影响因素与预测变量之间的拟合函数关系[13]，客流预测时需要为历史数据建立近似模型，参数训练调整复杂，可移植性较弱，且通常用于网络稳定情况下基于固有的稳定客流规律预测未来客流，不适用于客流波动性较大的新站开通初期客流精细化预测需求。

相对于参数回归方法，非参数回归方法摒弃传统求解数学解析模型的过程，不对数据做任何严格限定，且算法效率高，可移植性强。张晓利[13]、张涛[14]等对短时交通流量进行预测时，比较了非参数回归和神经网络的预测效果，证明了前者较后者具有更高精度和更强移植性。王翔[15]等对高速公路短时行程时间进行预测，证明非参数回归比时间序列自回归模型有更好的预测准确度与实时性。刘美琪[16]等研究了非参数回归在城市轨道交通进站客流量短时预测中的应用，比较了非参数回归、卡尔曼滤波模型和贝叶斯组合预测模型的预测效果，发现非参数回归的总体预测精度最高，能很好地适应城市轨道交通客流的复杂时变性和不确定性。但该研究依赖大量历史数据，无法适应新站开通初期缺乏数据的情况，同时采用传统K近邻非参数回归方法时，近邻值K固定不变无法适应实时预测，且算法只注重对客流分时比例的把握，缺少对客流量差异性的考虑。

针对新站开通初期实时进出站客流量预测，不仅需要解决历史数据缺乏的难点，同时要考虑预测方法能否把握开通初期客流不稳定的复杂时变特征。因此，本文以广州地铁广佛线二期开通为例，分析新站开通初期客流变化规律及其与车站周边土地利用性质的相关性，基于相同土地利用性质的既有车站客流数据，构建新站开通初期客流预测的历史数据库；结合实时进出站客流特征，考虑客流量的差异，对K近邻非参数回归方法中状态向量及K值的确定、预测算法等做出改进，提出新站开通初期实时进出站客流量预测方法；利用广州地铁实际数据对该方法进行验证。

1　新站开通初期客流特征

1.1　新站开通初期客流变化规律

广州地铁广佛线二期全长约为6 km，2015年12月28日开通，新开通的车站包括鹤洞、沙涌和燕岗3个车站。采用广州市轨道交通自动售检票系统(简称AFC系统)采集的15 min进、出站客流量，计算15 min进、出站客流分时系数(其值分别为15 min的进、出站客流量占全日总进站、总出站客流量的比值)，用于分析客流变化规律。由于进站客流与出站客流的分析方法相同，且变化规律一致，此处以进站客流量为例，分析各新站开通当天及之后若干平常日的进站客流变化规律。其中平常日指除节假日、大型活动等特殊日期的正常工作日和周六日。

鹤洞站15 min进站客流分时系数变化曲线如图1所示。由图1可知：鹤洞站开通初期，工作日内客流虽已具有一定周期性，但仍有大幅波动，短时间内甚至发生突变，客流变化规律较不稳定，且与周六日存在较大差异。进一步地，对AFC系统采集的客流数据进行统计，得到鹤洞站开通后前8个月内各月日均进站客流量，如图2所示。由图2可知：日均进站客流量在前3个月(自然月)变化较大，从第4个月开始呈稳定增长。同样，沙涌站和燕岗站的客流变化也表现出相同规律。

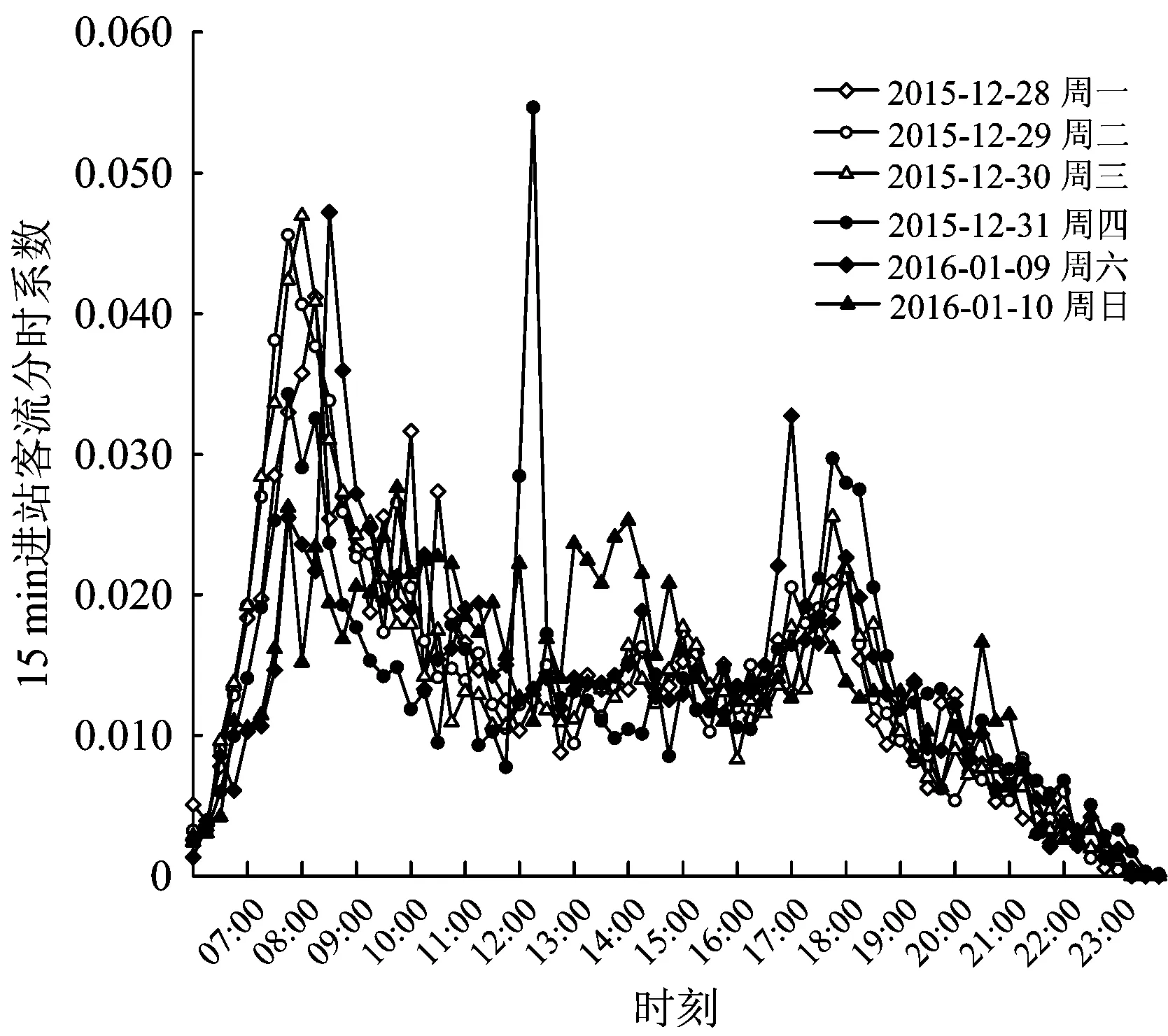
图1　鹤洞站15 min进站客流量变化曲线

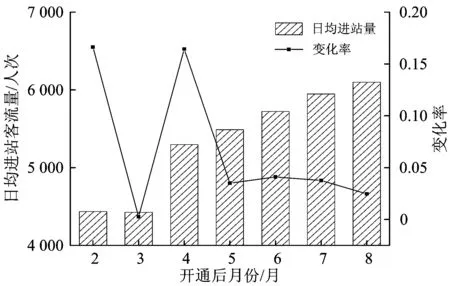
图2　鹤洞站日均进站客流量及其变化率

因此，若采用传统的客流预测方法，在新站开通初期的不稳定客流数据中寻找适应实时精准预测的动态映射关系显然不够理想，而非参数回归方法不需确定具体的函数关系，直接从客流数据中获取相关信息，能够更好地适应新站开通初期不稳定客流的预测。

然而，新站开通初期缺乏历史数据，没有历史客流变化规律作为未来短时间内客流预测的依据与参考，使得非参数回归方法也难以直接应用。因此，构建新站开通初期实时进出站客流量预测的历史数据库是本研究的首要任务。

1.2　新站进出站客流与周边土地利用性质的相关性

城市轨道交通客流发生与客流吸引的源泉是土地利用，即进出站客流在全天不同时间段上的分布规律很大程度上由车站沿线的土地利用性质决定[1]。土地利用性质主要分为居住类、办公类、居住占优类、办公占优类、商业类、枢纽类、综合类等，当车站周边土地存在混合利用的情况时，在不同时间段用于表征车站客流产生/吸引量的土地利用性质可能会发生改变，如工作日为办公占优类，周六日可能变为商业类。根据对鹤洞站周边土地利用情况的调研分析可知，其周边土地利用以居住区为主，含小规模的办公区，故可将其归为居住占优类车站。以工作日为例，取其15 min进、出站客流分时系数(其中进站为正，出站为负)观察新站进、出站客流变化规律。鹤洞站的进、出站客流分时系数变化规律如图3(a)所示，可见该站客流有明显的进站和出站早晚高峰，并且早高峰时进站客流大于出站客流，晚高峰时相反。在既有车站中，东晓南车站周边土地利用情况与鹤洞站相似，同属居住占优类的东晓南车站，其进、出站客流分时系数变化规律曲线也如图3(a)中所示，可见东晓南车站的进、出站客流分时系数变化规律与鹤洞站非常相似。沙涌站和燕岗站也归为居住占优类车站，与东晓南车站的客流分时系数变化规律同样一致。另外，在广州地铁网络中，选取其他相同土地利用性质的既有车站进行分析，如图3(b)至图3(d)所示，可以看出相同土地利用性质的车站进出站客流分时系数变化规律均存在较高的相似性。

图3　不同土地利用性质车站进、出站客流分时系数的变化规律

由此可见，基于进站、出站客流分时系数变化规律与车站周边土地利用性质的内生关系，建立新站与既有车站之间的映射，采用相同土地利用性质既有车站(简称为相似既有车站)的历史客流数据，可以构建新站实时进出站客流量预测的历史数据库。

2　基于改进非参数回归的新站开通初期实时进出站客流量预测方法

根据新站开通初期实时进出站客流特征，对K近邻非参数回归方法做出改进，提出适用于新站开通初期的实时进出站客流量预测方法。

K近邻非参数回归预测方法的核心思想是数据库模式匹配，即从历史数据库中提取数据特征，根据合理的状态向量找到与当前实时观测数据相匹配的K个近邻数据，将其作为预测算法的输入，最终得到下一时段的客流预测值。该预测方法包括构建历史数据库、确定状态向量、制定相似机制、近邻K值的选取和预测算法5个步骤。

2.1　历史数据库的构建

首先，基于模糊C均值聚类方法选取与新站土地利用性质相同的既有车站，构建相似既有车站客流基础数据库。根据对不同土地利用性质车站进出站客流分时系数变化规律的分析，可发现进出站客流早晚高峰的客流特征与车站周边土地利用性质具有直接关联，故选取早晚高峰系数(其值为早晚高峰时段内15 min进、出站客流分时系数的总和，即早晚高峰时段内客流量占全日总客流量的比值)作为车站聚类指标。对不同时间、不同位置的城市轨道交通网络中所有既有车站进行模糊C均值聚类[17]，其中既有车站的位置通过既有路网车站可达性[18]进行划分。基于聚类结果，构建车站性质匹配库，以描述预测日时间属性、新站的车站位置、新站的土地利用性质与既有车站的映射关系。如对于新站X，则有

DML:SX=f(TP,SL,ST)

(1)

式中：DML为车站性质匹配库，包括性质相匹配的所有既有车站；SX为新站X匹配得到的相似既有车站集；TP为预测日时间属性对应指标；SL为新站车站位置指标；ST为新站周边土地利用性质指标。其中新站X的车站位置和周边土地利用性质可以根据城市地图进行确定。

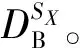
其次，构建新站客流基础数据库。新站开通运营后，新站的客流数据较相似既有车站的客流数据更能直接体现其客流变化规律，故应将新站的客流数据及时加入历史数据库。

最后，基于新站及既有车站客流基础数据库，确定历史客流数据的时间跨度，构建历史数据库。历史数据库的构成，一方面应尽量多的包含未来可能发生的客流变化规律，同时也不能过于冗余，以免影响预测的实时性。因此，历史数据库的构成可表示为

(2)

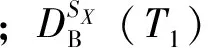
对于时间跨度T1，因不同新站的相似既有车站数目不一，需结合实际合理确定。同时，随着新站客流数据的不断积累，时间跨度T2需逐日增加，即T2=dt-d0(其中，d0为新站开通日，dt为预测日)。当新站开通一段时间后，且自身客流数据足以代表未来客流变化趋势时，应从历史数据库中剔除相似既有车站的客流数据，以避免数据库冗余。

此外，对于历史数据库中客流数据的时间属性，需要与预测日时间属性保持一致，即若预测日为工作日，则历史数据库中均为工作日的客流数据。随着新站客流数据的逐渐积累，可对历史数据库进一步细分，如将平常工作日的历史数据库分成周一至周五分别进行构建，以提高算法预测效率及精度。

历史数据库的形成过程可以简要表述如图4所示。

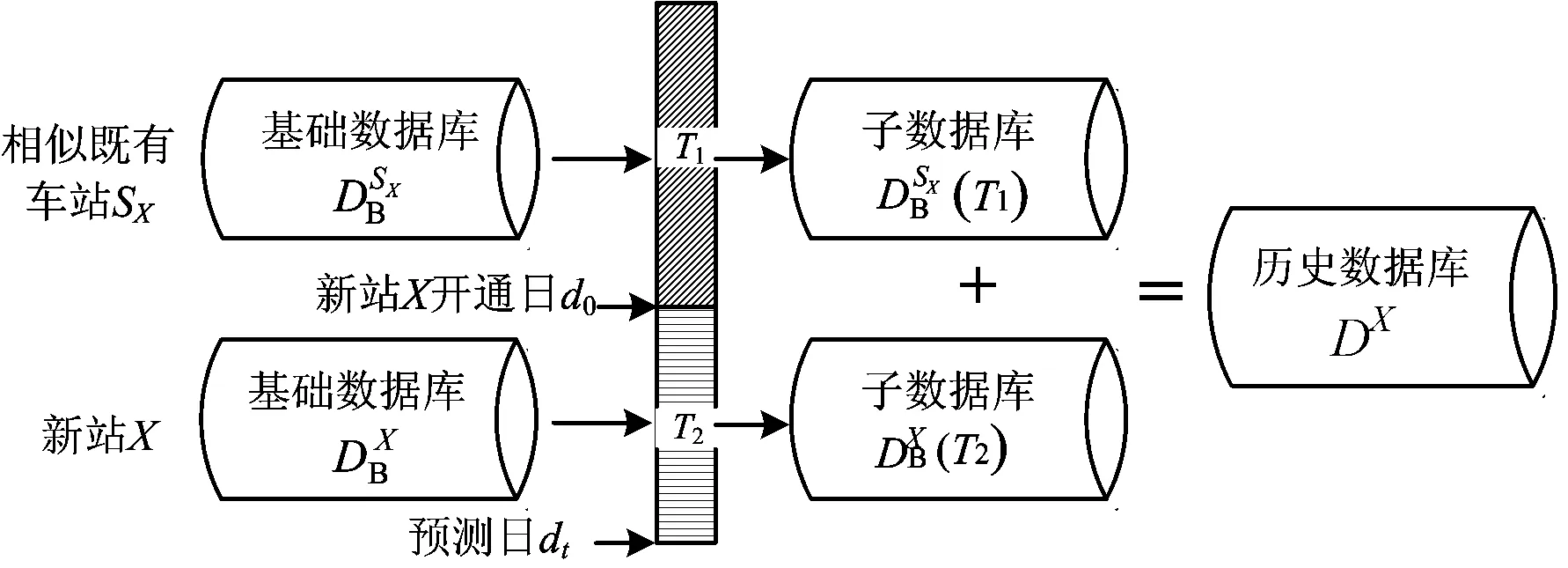
图4　历史数据库形成示意图

2.2　基于时间序列自相关性的状态向量确定

不同时段的实时进、出站客流量均可看作独立的1个时间序列，在各时间序列中，连续若干时间段的客流量间具有较强的关联，因此选取与预测时段进、出站客流量最密切相关的若干相邻时段的进、出站客流量作为状态向量。具体方法是：通过计算q阶自相关系数rq确定状态向量中前m个时段的客流量，即将连续n个时间段的进或出站客流量看作时间序列{Q(1),Q(2),…,Q(n)}，则这个时间序列q阶自相关系数rq的计算公式为

(3)

其中，

通常，对于给定的自相关系数阈值M，当相关系数rq≥M时，可认为时间序列中间隔q个时段的2个值相关性较强。为使状态向量中尽可能多地包含与预测时段相关的客流时段，取m=max{q|rq≥M}， 即m为满足rq≥M的最大q值， 并由预测时段前m个时段的进或出站客流量构成状态向量。

2.3　相似机制及近邻K值的确定

传统非参数回归方法，在匹配近邻数据时，用欧式距离作为指标衡量实时数据与历史数据的匹配程度，欧式距离的取值范围为[0,∞)，为了与通常的相似程度判别方法(即1表示最为相似，0表示完全不相似[19])更为一致，本文采用相似度测度函数替代欧式距离作为近邻匹配机制。相似度测度函数为

(4)

式中：A和H分别为实时数据和历史数据中同一时段的状态向量；ak和hk分别为实时和历史状态向量中各时段进或出站客流量；K为近邻的个数；c为常量，用于调节相似度的分布。

目前，对于近邻个数K的取值没有既定准则。大多研究通过对不同K取值下一定量样本的测试结果进行误差判断，确法最优K值，并在预测时始终取该值。不同于既有研究，本文在实时客流预测时，动态计算每个预测时段的K值，即以历史数据库中预测日前Nk天对应时段的客流为预测样本，计算得到Nk个最优K值，并取其均值作为当前预测时段的K值。

2.4　考虑客流量差异性的改进算法

根据前文分析，新站与相同土地利用性质的既有车站之间进出站客流分时系数变化规律高度相似，但客流量不完全相近。例如，同为办公类车站的珠江新城站与林和西站，客流分时系数变化规律非常相似，如图5所示，但分时客流的量级存在较大差异，如图6所示。同时，同一车站的进出站客流量由于一定的自然增长同样存在客流量上的波动，因此，为减小预测客流量与近邻客流量的差异，本文定义近邻系数，其计算公式见式(5)，用以调整近邻的客流量，调整计算公式见式(6)。对珠江新城站客流进行调整，调整后的客流量与林和西站的客流量非常相近，如图6所示，这说明通过近邻系数的调整能够有效减小客流量的差异。

(5)

(6)

图5　分时系数对比

图6　调整前后分时客流量对比

以实际数据与近邻数据的相似度为权重，相似度越大权重越大；采用基于相似度的加权平均法，得到预测时段t的客流预测值y(t)，计算方法为

(7)

其中，

式中：si为第i个近邻状态向量与当前状态向量间的相似度；αi为第i个近邻预测值的权重。

3　实例分析

以广州地铁广佛线二期开通的鹤洞、沙涌和燕岗3个新站为例，这3个新站均属于居住占优类车站。尽管本文所提出的方法适用于新线开通初期进出站客流量的实时预测，但考虑到文章篇幅的限制，以下以开通前半年内的广州地铁线网既有车站客流数据作为历史客流数据，采用本文提出的方法，仅对该线路新站开通后的实时进站客流进行预测，时间粒度为15 min，预测场景为平常工作日。

3.1　历史数据库构建

广州地铁全网共有136个既有车站，对其进行模糊C均值聚类。结合广州地铁运营现状，工作日早晚高峰时段分别为7:00—9:00和17:00—19:00，计算这2个时间段内客流量占全日总客流量的比值，即为早、晚高峰系数，将其作为聚类指标，对工作日的全网既有车站进行聚类，结果见表1。

表1　工作日车站聚类结果

由表1可知：既有车站中居住占优类车站有三元里、东晓南、江南西等共14个车站，考虑相似既有车站较多，取新线开通前半年内的客流数据，再加入新站开通后逐日形成的客流数据，由此构成历史数据库。

为适时剔除既有车站客流数据，分析近邻匹配结果中既有车站客流与新站客流的占比。结果显示：新站开通后的前4个月，既有车站的匹配比例依次为95.33%，55.00%，28.00%，19.53%，反之新站本站客流的匹配比例逐月上升。即随着新站开通后时间的推移，本站的历史客流量更能体现本站未来客流量变化趋势。因此，考虑到预测算法的运行效率，新站开通3个月后，剔除历史数据库中既有车站的客流数据，即令T1=0。

另外，新站开通初期，因本站客流数据量较少，在数据库构建时，将所有的平常工作日数据汇集在一起构建工作日的历史数据库。在新站开通3个月后，随着新站数据量不断增大，考虑到同一周次的客流规律相似度更高，可将历史数据库进一步细化，分别针对周一至周五等5个工作日构建历史数据库，以提高算法的预测效率。

3.2　模型参数确定

状态向量的确定。根据广州地铁全网既有车站半年内平常工作日15 min进站客流量，以每日每车站60个(7:00—22:00)时段进站客流量为1个样本序列，共计19 312条样本。根据式(3)计算样本各阶自相关系数，取阈值M=0.5，统计所有样本中rq≥0.5的占比，结果见表2。

表2　　　　各阶自相关系数满足阈值条件(rq≥0.5)的占比统计

由表2可知：样本中q=1，2，3时，均有90%以上样本数据满足rq≥0.5，而q=4时，满足要求的样本量低于30%，可认为实时进站客流量中，预测时段进站客流量与前3个时段进站客流量具有较强相关性。因此，确定平常工作日场景下进站客流量预测时m=3，即本文提出的方法适用于当日15 min的实时客流量采集时段已满足3个的情况。

近邻K值的确定。参照相关研究[14]结论，本文取Nk=10，表3列出燕岗站部分时段预测时的K取值，由于每日每时段均重新计算K值，且各时段取值不尽相同，本文不再一一列举。

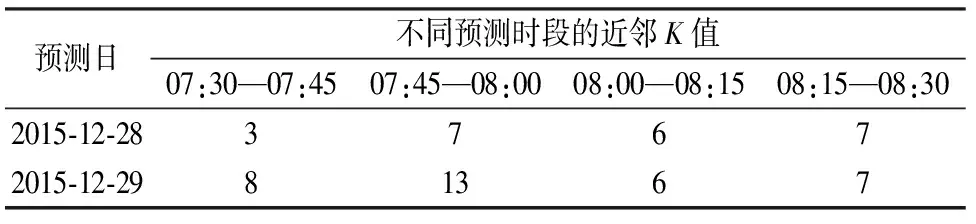
表3　燕岗站部分时段近邻K值

3.3　模型预测精度分析

基于实际数据，定义a(t)为预测时段t实际的进站客流量，将本文方法的预测结果与实际值进行对比分析，采用平均绝对误差MAE与平均绝对百分比误差MAPE对模型进行精度检验，其计算公式见式(8)和式(9)，预测结果见表4。

(8)

(9)

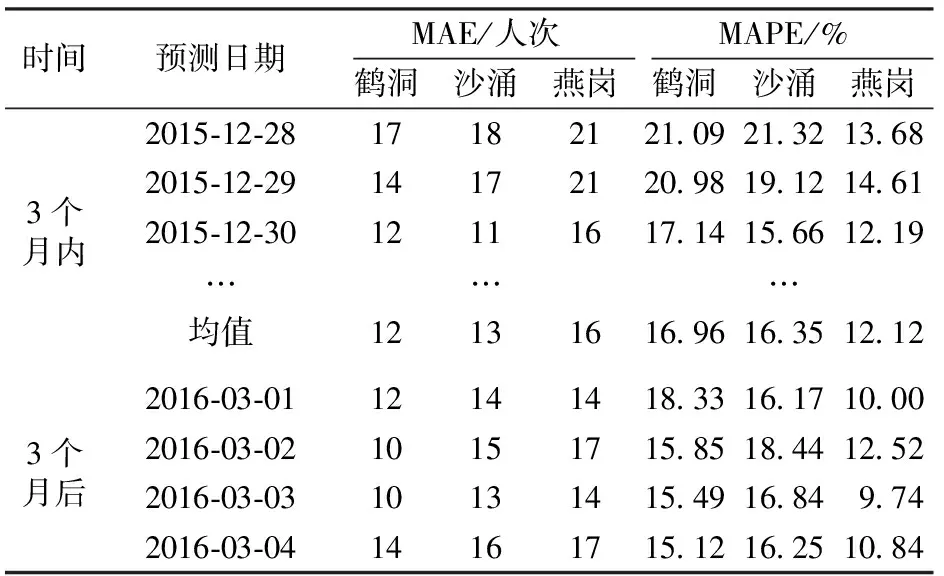
表4　新站部分日期实时进站客流量预测误差

根据误差统计，各新站开通当天平均绝对百分比误差均在22%以下，鹤洞、沙涌的误差略大于燕岗，分析原因发现，鹤洞、沙涌站的客流规模小，基础客流量较小，导致相对误差略大。前3个月的平均MAE不超过16人次，平均MAPE在17%以下。为更具体地分析15 min进站客流量预测误差，取燕岗站2015-12-30的实时进站客流量预测值与实际值进行比较，如图7所示，由图7可以看到数据点基本分布在45°线附近，说明预测结果较为理想。

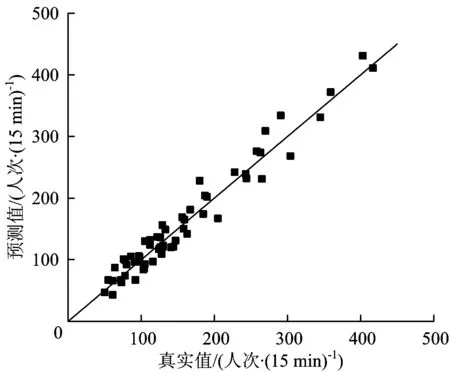
图7　燕岗站预测值与真实值对比

为验证本文提出的改进算法的有效性，以预测燕岗站2015-12-30实时进站客流量为例，分别采用不考虑客流量差异性的传统非参数回归方法和本文方法进行预测。结果表明，采用传统预测方法的平均绝对误差为23人次，平均绝对百分比误差为17.23%；采用本文方法的预测误差分别为16人次和12.19%。可见，本文提出的改进算法预测精度更优于传统非参数回归算法。

此外，由表4还可以看到，随着开通时间的推移，预测误差有一定变化。为进一步分析该方法的预测效果，结合历史数据库的不同组成，对新站开通后连续4个月内平常工作日实时进站量进行预测，统计得到周平均预测误差，如图8所示。由图8可知：随着历史数据库中本站客流量的增多，各新站的实时进站客流量预测精度会逐渐提高直至平稳。该结果说明：随着预测时间跨度的增大，本站历史客流量逐渐积累，对历史数据库进一步细分后，本文提出的方法可以得到较好的预测效果，说明本文的预测方法具有良好的适应性。

图8　模型预测精度变化

4　结　论

本文分析了城市轨道交通新站开通初期客流的变化规律，发现新站开通初期3个月内客流量波动较大，而后客流量变化趋于稳定。为解决新站开通初期客流预测中历史数据缺乏的问题，本文提出了基于相同土地利用性质的既有车站历史客流数据的新站开通初期客流预测的历史数据库构建方法，然后针对新站开通初期客流波动大等问题，结合新站实时客流特征，提出了基于改进非参数回归方法的新站实时进出站客流量预测方法。其中，针对实时预测改进了状态向量及近邻K值的确定方法，并考虑客流量差异性对预测算法做出调整，以提高算法的预测精度达到实时客流精准预测的要求。

以广州地铁广佛线二期新站开通初期的实际进站客流量预测为例，对本文方法的预测效果进行了验证。结果显示：各新站实时进站量预测的平均绝对误差不大于16人次。此外，随着新站客流量数据不断积累，该方法的预测精度会逐渐提高，说明该方法在数据量充足的情况下能够更加精确地预测实时进出站客流量，实现车站及网络客流的实时监测，为新站开通后及时制定并实施运输组织计划提供重要的决策依据。

[1]光志瑞.基于土地利用和可达性的城市轨道交通进出站客流量预测[D].北京:北京交通大学,2013.

(GUANG Zhirui. Passenger Flow Prediction for Urban Railway Station’s Entrance and Exit Based on Land-Use and Accessibility [D]. Beijing: Beijing Jiaotong University, 2013. in Chinese)

[2]蔡昌俊,姚恩建,张永生,等. 基于AFC数据的城轨站间客流量分布预测[J].中国铁道科学,2015,36(1):126-132.

(CAI Changjun, YAO Enjian, ZHANG Yongsheng, et al. Forecasting of Passenger Flow’s Distribution among Urban Rail Transit Stations Based on AFC Data[J]. China Railway Science, 2015,36(1):126-132. in Chinese)

[3]程涛,周峰,郦海通.西安地铁2号线南段运营初期客流预测[J].都市快轨交通,2015,28(5):45-49.

(CHENG Tao, ZHOU Feng, LI Haitong. Forecasting Passenger Flow on Southern Extension of Xi’an Metro Line 2 in Preliminary Operation Stage[J]. Urban Rapid Rail Transit,2015,28(5):45-49. in Chinese)

[4]赵路敏,王奕,杜世敏.新线开通对线网客流特征的影响[J]. 都市快轨交通,2011,24(2):46-49.

(ZHAO Lumin, WANG Yi, DU Shimin. Impact of Opening a New Line on Passenger Flow Feature ofUrban Rail Transit Network[J]. Urban Rapid Rail Transit, 2011,24(2):46-49. in Chinese)

[5]JAN G De Gooijer, ROB J. Hyndman. 25 Years of Time Series Forecasting[J].International Journal of Forecasting,2006，22(3):443-473.

[6]WILLIAMS B M, HOEL L A. Modeling and Forecasting Vehicular Traffic Flow as a Seasonal ARIMA Process: Theoretical Basis and Empirical Results[J]. Journal of Transportation Engineering, 2003, 129(6):664-672.

[7]OKUTANI I, STEPHANEDES Y J. Dynamic Prediction of Traffic Volume through Kalman Filtering Theory[J]. Transportation Research Part B: Methodological, 1984, 18(1): 1-11.

[8]张春辉, 宋瑞, 孙杨. 基于卡尔曼滤波的公交站点短时客流预测[J]. 交通运输系统工程与信息, 2011, 11(4): 154-159.

(ZHANG Chunhui, SONG Rui, SUN Yang. Kalman Filter-Based Short-Term Passenger Flow Forecasting on Bus Stop[J].Journal of Transportation Systems Engineering and Information Technology,2011,11(4):154-159. in Chinese)

[9]杨军,侯忠生.基于小波分析的最小二乘支持向量机轨道交通客流预测方法[J].中国铁道科学,2013,34(3):122-127.

(YANG Jun, HOU Zhongsheng. A Wavelet Analysis Based LS-SVM Rail Transit Passenger Flow Prediction Method[J]. China Railway Science, 2013,34(3):122-127. in Chinese)

[10]SUN Yuxing, LENG Biao, GUAN Wei. A Novel Wavelet-SVM Short Time Passenger Flow Prediction in Beijing Subway System[J]. Neurocomputing,2015(166):109-121.

[11]YU Wei, MU Chen Chen. Forecasting the Short-Term Metro Passenger Flow with Empirical Mode Decomposition and Neural Networks[J]. Transportation Research Part C,2012(21):148-162.

[12]董升伟.基于改进BP神经网络的轨道交通短时客流预测方法研究[D].北京交通大学,2013.

(DONG Shengwei.The Research of Short-Time Passenger Flow Forecasting Based on Improved BP Neural Network in Urban Rail Transit[D]. Beijing: Beijing Jiaotong University, 2013. in Chinese)

[13]张晓利,陆化普.非参数回归方法在短时交通流预测中的应用[J].清华大学学报:自然科学版,2009,49(9):1471-1475.

(ZHANG Xiaoli, LU Huapu. Non-Parametric Regression and Application for Short-Term Traffic Flow Forecasting[J].Journal of Tsinghua University：Science and Technology,2009,49(9):1471-1475. in Chinese)

[14]张涛,陈先,谢美萍,等.基于K近邻非参数回归的短时交通流预测方法[J].系统工程理论与实践,2010,30(2):376-384.

(ZHANG Tao, CHEN Xian, XIE Meiping, et al.K-NN Based Nonparametric Regression Method for Short-Term Traffic Flow Forecasting[J].System Engineering-Theory & Practice, 2010,30(2): 376- 384. in Chinese)

[15]王翔,陈小鸿,杨祥妹.基于K最近邻算法的高速公路行程时间预测[J].中国公路学报,2015,28(1):102-111.

(WANG Xiang, CHEN Xiaohong, YANG Xiangmei. Short Term Prediction of Expressway Travel Time Based onKNearest Neighbor Algorithm[J].China Journal of Highway and Transport, 2015,28(1): 102-111. in Chinese)

[16]刘美琪,焦朋朋,孙拓.城市轨道交通进站客流量短时预测模型研究[J].城市轨道交通研究,2015(11):13-17.

(LIU Meiqi, JIAO Pengpeng, SUN Tuo. On Short-Term Forecasting Model of Passenger Flow in Urban Rail Transit[J].Urban Mass Transit, 2015(11):13-17. in Chinese)

[17]姚恩建,李斌斌,刘莎莎,等.考虑土地利用性质匹配度的城轨客流分布预测[J].交通运输系统工程与信息,2015,15(6):107-113.

(YAO Enjian, LI Binbin, LIU Shasha, et al. Forecast of Passenger Flow Distribution among Urban Rail Stations Considering the Land-Use Matching Degree[J]. Journal of Transportation Systems Engineering and Information Technology, 2015,15(6):107-113. in Chinese)

[18]姚恩建,程欣,刘莎莎,等.基于可达性的城轨既有站进出站客流预测[J].铁道学报,2016,38(1):1-7.

(YAO Enjian, CHENG Xin, LIU Shasha, et al. Accessibility-Based Forecasting on Passenger Flow Entering and Departing Existing Urban Railway Stations[J]. Journal of the China Railway Society, 2016,38(1):1-7. in Chinese)

[19]李星毅.基于相似性的交通流分析方法[D].北京:北京交通大学,2010.

(LI Xingyi. Methods of Traffic Flow Analysis Based on Similarity[D]. Beijing: Beijing Jiaotong University, 2010. in Chinese)