致灾因素耦合作用下堆积体斜坡失稳概率研究

　，，　

(成都理工大学 地质灾害防治与地质环境保护国家重点实验室，成都　610059)

1　研究背景

川藏交通廊道沿线藏东南地区地质环境复杂，具有深切峡谷、高烈度、气候环境恶劣等特点。区域活动断裂分布广泛，崩滑流地质灾害十分发育[1-2]。大量研究表明，沿线广为分布的斜坡堆积体易在极端诱发条件下失稳，成为藏东南入藏道路建设与长期运营的潜在风险。并且，由于深切峡谷的地貌特征，大型堆积体滑坡还可能为其他地质灾害的发生提供物质基础[3]，形成灾害链式效应，导致灾害范围与损失进一步扩大，例如滑坡导致堰塞堵江，并且一处断道，全线瘫痪，后果严重。因此，对此类型“沟谷型崩滑堆积体”定量评价其失稳风险对交通安全运营有至关重要的作用。

崩滑堆积体由于生成过程具有内在不确定性，力学性质表现出显著的空间变异性；另一方面，由于环境条件复杂，外界诱发因素的随机性同样对斜坡稳定产生很大的影响。因此，为了对滑坡危险性作出准确预测，需要采用概率研究的方法，综合考虑坡体物理力学参数的不确定性及外界诱发因素的随机性。何朋朋等[4]考虑地震与地下水的随机性，基于不平衡推力法利用蒙特卡罗模拟(MCS)进行了滑坡可靠性分析；张璐璐等[5]、Tung等[6]基于水-土特征曲线及渗透系数数据的统计分析，分别讨论了渗流参数的变异性及相关性对斜坡可靠度的影响；蒋水华等[7]通过研究发现土体渗透系数空间变异性对潜水面和滑面位置均有明显的影响；王贺等[8]基于湿润锋位置的变化研究了降雨条件下残积土边坡的时变可靠度。

对于单体斜坡的危险性评价其难点在于失稳概率的计算。然而传统可靠度方法更加注重斜坡体物理力学参数的变异性，通常忽略诱发因素本身的不确定性；实际上，只有综合考虑致灾因素的随机性与诱发过程的不确定性才能得到完整意义上的危险性[9]。虽然有部分学者考虑了外界诱发因素的随机作用，如陈丽霞等[10]将降雨拟合为极值分布，分别计算了不同重现期的极值降雨条件下的滑坡失稳概率;鲍叶静等[11]通过概率地震危险性方法(PSHA)进行了地震诱发滑坡概率的初步预测，但上述分析只考虑单一诱发因素的作用，没能将多种随机致灾因素耦合分析。实际上，耦合考虑多致灾因素的分析对实际工程风险评价能够提供更全面的指导信息，因为在气候地质环境复杂的地区，仅考虑一种触发因素的危险性评价是不够符合实际，且不够合理的。

为了进一步拓展随机致灾作用下的斜坡危险性研究，本文综合考虑外界诱发因素自身的随机性与诱发作用的不确定性，通过分析不同量级诱发事件的发生概率与回归周期，结合蒙特卡罗模拟计算对应诱发事件作用下的斜坡失稳概率，揭示不同程度的滑坡危险性序列。在此基础上进行多致灾因素的耦合计算，系统评价堆积体斜坡的危险性与潜在风险。

2　多重致灾因子耦合下斜坡失稳概率计算方法

大量研究认为，诱发斜坡失稳的主要致灾因素有降雨、地震、库水位变动以及人类工程活动等，并且大量的滑坡实例也证明了滑坡几乎不会同时被多个致灾因素所诱发，但危险性评价时需要考虑存在多种致灾因素的情形[12]。

基于上述特点，本文利用全概率公式(式(1))来表达滑坡灾害存在多种致灾因素共存，但又不会同时被多种因素触发的情形。

(1)

式中：P(B)为耦合诱发因素作用下滑坡失稳全概率；P(B|Ai)为不同量级诱发条件下滑坡失稳概率；P(Ai)为不同量级诱发因素出现概率。

斜坡在诱发事件作用下的失稳概率为一条件概率，且不同诱发因素之间相互独立，同一诱发因素下不同量级诱发事件可视为互斥。据此根据全概率定理可得到耦合作用下不同程度的滑坡危险性序列。本文将以地震、降雨2种典型致灾因素为例对本研究方法进行说明。

2.1　降雨诱发作用下失稳概率

2.1.1降雨因素的随机性

已有研究表明引发降雨型滑坡的是某种极值降雨参量[10]，不同区域的极端降雨也表现出某种分布的特征。据此通过将极值降雨看作随机变量，利用其分布特征获得某种危险性量级的极值降雨的发生概率与回归周期。

2.1.2非饱和入渗作用下斜坡失稳概率分析

作为最为常见的滑坡诱发因素，大量研究认为降雨作用于斜坡失稳机理在于随着雨水入渗，含水率提高，坡内土体基质吸力减小，抗剪强度降低，改变了坡体内原来的力学平衡，从而引发斜坡失稳[13-14]。

本文采用有限元软件SEEP/W模拟降雨入渗引起的暂态渗流场，其控制方程为

(2)

式中：kx，ky分别是x，y方向的渗透系数；H为压力水头；θ为体积含水量;Q表示系统流入和流出的差值，当Q=0时即为稳态渗流。稳态渗流时，式(2)等号右边为0。水-土特征曲线(SWCC)选取常用的Fredlund-Xing模型为[15]

(3)

式中：θw(ψ)为土的体积含水量函数；θs和ψ分别为饱和体积含水量及基质吸力；α，n和m均为SWCC的拟合参数；e为自然对数;C(ψ)为修正函数，其具体计算方法参见文献[15]。在此基础上，通过对整个体积含水量函数进行积分即可得到渗透系数函数[15]为

(4)

式中：kw为负孔压计算所得渗透系数；ks为饱和渗透系数;y为代表负孔压算法的虚拟变量；j和N分别为最终函数描述的最小负孔压、最大负孔压。

将计算得到的暂态孔隙水压力分布导入极限平衡分析程序SLOPE/W中，并采用Morgenstern-Price(M-P)法并结合蒙特卡罗模拟(MCS)对斜坡的稳定可靠度进行计算。通过SLOPE/W自动进行滑面的搜索试算，并确定最小安全系数的关键滑面。土体强度模型为考虑基质吸力的双应力变量状态模型，其表达式为

τ=c′+(σn-ua)tanφ′+

(5)

式中：c′，φ′分别为有效黏聚力和有效内摩擦角；σn为法向应力；ua，uw分别为孔隙气压力和孔隙水压力；θr为残余含水量。

其中，为充分考虑不确定性，将上述参数c′,φ′视作随机变量，利用MCS对其分布进行随机抽样，此时斜坡失稳概率表达为计算所得安全系数<1的次数与总的模拟次数的比值。

2.2　概率地震滑坡危险性分析方法

目前主流的地震斜坡稳定性评价方法中，拟静力法由于将地震荷载视作方向、大小不变的静荷载，其结果往往过于保守；动力有限元法虽然理论上能够得到最为精确、可靠的斜坡地震动响应，但在实际应用中，有较多参数难以获取并且计算过程复杂，大大限制了该方法的应用。而Newmark累积位移法在近年来发展迅猛，其量化了边坡的受损程度，为坡体稳定性判识提供了一种可靠的依据[16]，被认为是平衡上述2种方法的桥梁[17-18]。

2.2.1地震Newmark累积位移方法

Newmark累积位移法通过位移指标对斜坡在地震作用下的稳定性进行评价，认为滑体累积位移是在地震荷载作用下，滑(块)体克服底滑面摩擦阻力后沿着滑动面位移不断累积所致。通过确定潜在滑体(刚塑性体)的临界(或屈服)加速度ac，当输入地震动加速度大于临界加速度时，滑(块)体开始沿着无限斜坡面滑动，将加速度时程中大于临界加速度的部分对时间进行二次积分即可得到累积位移量。Newmark位移计算的二次积分示意图如图1所示。

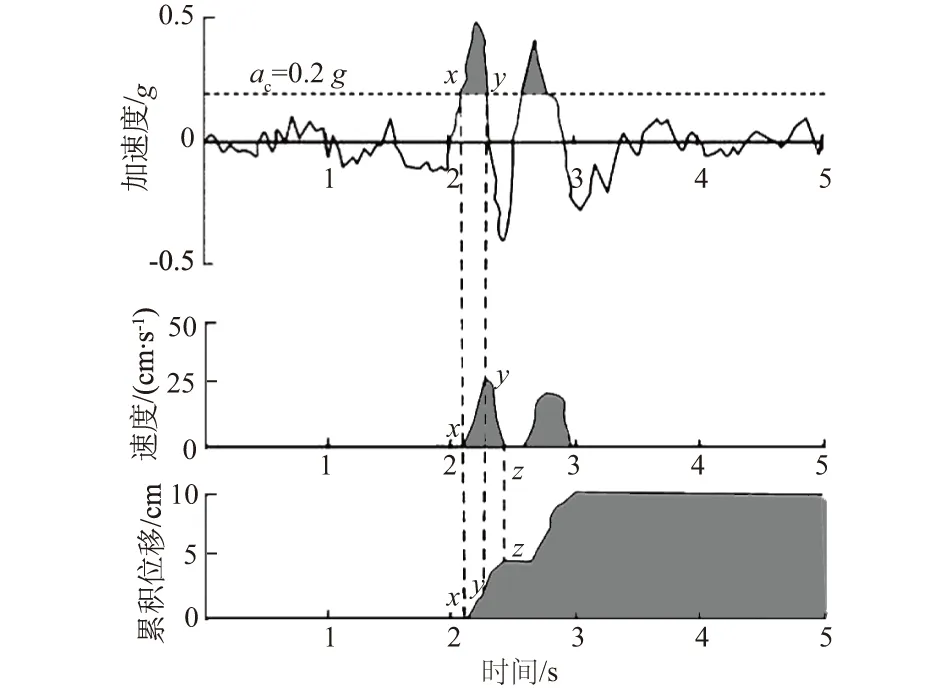
图1　Newmark位移计算的二次积分示意图[17]Fig.1　Illustration of the Newmark doubleintegration algorithm[17]

经过多年的改进之后，临界加速度ac的表达式为[19]

ac=(Fs-1)gsinα。

(6)

其中，

(7)

式中：Fs为静态安全系数；c′,φ′分别为滑体有效内聚力与有效内摩擦角；m为滑体中地下水位的高度；z为滑块体厚度；γw，γ分别为水与滑(块)体的重度。

2.2.2基于Newmark位移模型的概率地震滑坡危险性评价

随着风险研究的开展，许多学者研究了地震动参数与Newmark累积位移的关系[20-21]，基于强震地震动记录的地震诱发斜坡累积位移回归模型也因此被广泛应用于区域地震滑坡的风险评价、具体边坡工程地震稳定性的快速预估。

同时，由于累积位移模型具有地域相关性，我国学者徐光兴等[18]基于汶川地震记录拟合出4种不同参数的位移模型，并且推荐判定系数较高、PGA(峰值地震动加速度)最易获取且应用最为广泛的临界加速度比模型作为四川及邻近省区的地震滑坡风险预测模型，其表达式为

lgDn=0.194+

R2=91.4%。

(8)

式中：Dn为累积位移(cm)；R2为判定系数。

地震滑坡危险性评价中存在大量不确定性，不仅包括地震动参数的随机性，还包括斜坡体力学参数的不确定性，甚至累积位移模型自身的模型不确定性[22-24]。为了突出重点，本文暂不考虑位移模型的不确定性。

首先，通过传统地震危险性评价(PSHA)确定地震动参数的危险性量级及相应的超越概率(如50 a超越概率为10%)，据此通过式(8)计算给定地震动危险性等级的斜坡累积位移大于某位移阈值的年超越概率，其表达式为

λD(x)=P(Dn>x|PGA=z,ac)·MRDPGA(z)。

(9)

式中：P(Dn>x|PGA=z,ac)为给定地震动强度及临界加速度下累积位移超过某位移量级的概率；MRDPGA(z)为特定地震动强度的年超越概率。

其次，为充分考虑斜坡体参数的不确定性，将式(8)中临界加速度ac的自变量c′,φ′视作随机变量，ac的表达式见式(6)；从而能够以概率分布的形式表达临界加速度ac的取值；然后，通过蒙特卡罗模拟(MCS)对ac的分布进行随机抽样，最终得到累积位移Dn的分布形式[25]，即得到特定地震动等级下的斜坡累积位移的危险性曲线。

值得注意的是，计算得到的累积位移并非地震作用下斜坡产生的精确位移，但是它反映了斜坡变形累积的程度，可作为地震滑坡危险性的指标，即位移阈值的超越概率λD(x)为地震滑坡失稳概率。

3　工程实例

川藏交通廊道某堆积体斜坡为以1967年巨型崩塌堆积体为主的崩塌、滑坡、残坡积体复合型堆积体斜坡，位于西藏林芝县排龙乡境内，地处藏东南高山深切河谷地区，为一典型沟谷型崩塌堆积体(见图2)。

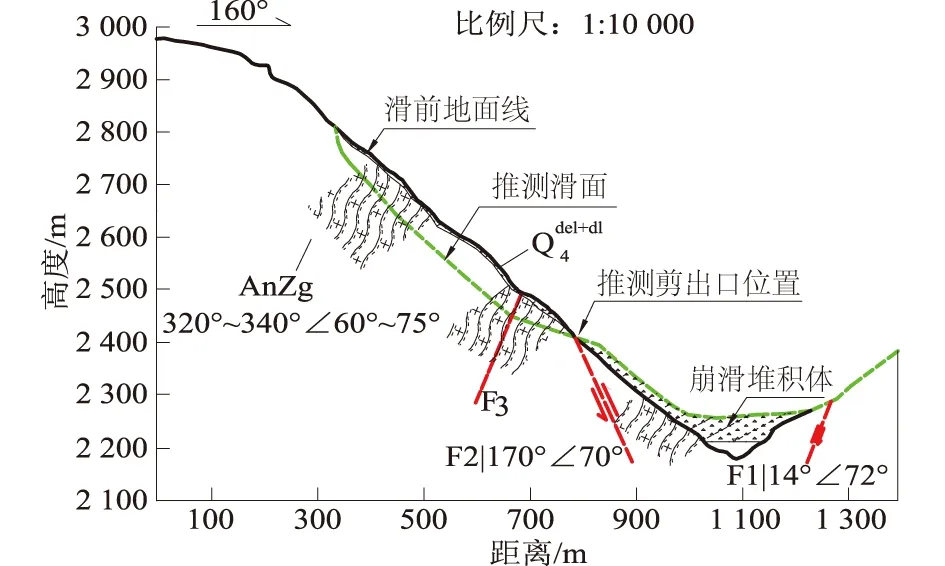
图2　某堆积体斜坡剖面图[26]Fig.2　Profile of a deposit slope[26]

巨型崩滑发生时，滑体分为东西2部分，无论从规模、滑动速度还是运动距离来讲，东滑块均远大于西滑块，是巨型崩滑的主体和危害最为严重的部分。本文述及的堆积体均指东滑块堆积体，其大部分堆积在坡体的中下部及斜坡坡脚位置，部分冲过东久河堆积在对岸300 m范围内。堆积体的厚度则呈中西部较薄，而东部相对较厚的特点，中、西部厚20～30 m，东部的厚度则>50 m，均厚45 m。

在巨型崩滑发生前后，地形变化明显，斜坡地形坡度总体变缓，整体呈上陡下缓的形态。物质组成以花岗片麻岩为主，含量为40%～60%，<2 mm的细粒物质含量占40%～50%。在细粒物质中，砂粒含量约占75%，粉黏土约占25%。

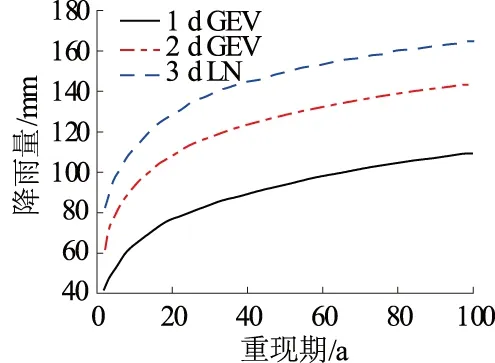
图3　西藏流域波密站最大3 d降雨量分布[26]Fig.3　Distribution ofmaximum 3 d rainfall atBomi station, Tibet[26]

3.1　降雨诱发作用下的失稳概率

张玉虎等[27]探讨了西藏区域不同降雨极值序列概率分布函数的适宜性，并对拟合的极值降雨分布进行了拟合优度检验，结果如图3所示,图中GEV，LN分别表示广义极值分布与对数正态分布。

为了充分反映极端降雨的触发作用，选取总降雨量值最大，同时也是拟合效果最佳的最大3 d降雨量(图3中3d LN曲线)作为降雨参量，从分布中得到不同危险性量级的降雨事件的年出现概率及重现期。

为考虑参数的随机性，利用勘察钻孔资料将崩滑堆积体的有效抗剪强度参数拟合分布如表1所示。同时，通过对饱和渗透系数的取值进行广泛的工程地质类比，最终确定水-土特征曲线参数α,n和m分别为2.575 kPa，4.247和0.391，饱和含水率为0.453。

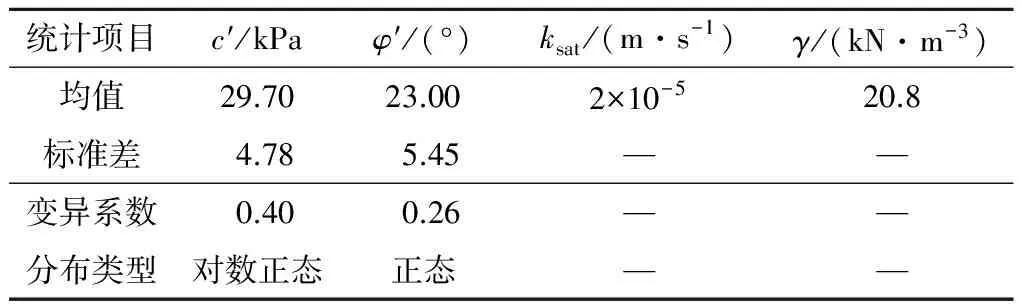
表1　某堆积体斜坡参数统计特征Table 1　Statistical parameters of a deposit slope

本文采用有限元软件SEEP/W模拟降雨入渗引起的暂态渗流场。基于前述所得不同回归周期的最大3 d降雨量，首先采用稳态分析模拟堆积体斜坡在常年平均降雨条件下(1 332.7 mm)的情况，即入渗强度为0.003 7 mm/d。在此结果基础上，采用瞬态分析分别按照重现期T为25，50，100 a的最大3 d降雨量设置入渗边界条件，即分别为0.045,0.050,0.055 m/d。取基覆界面为不透水边界，并设置前缘东久河为定水头边界。关键滑面安全系数和失稳概率与时间的关系分别如图4、图5所示。

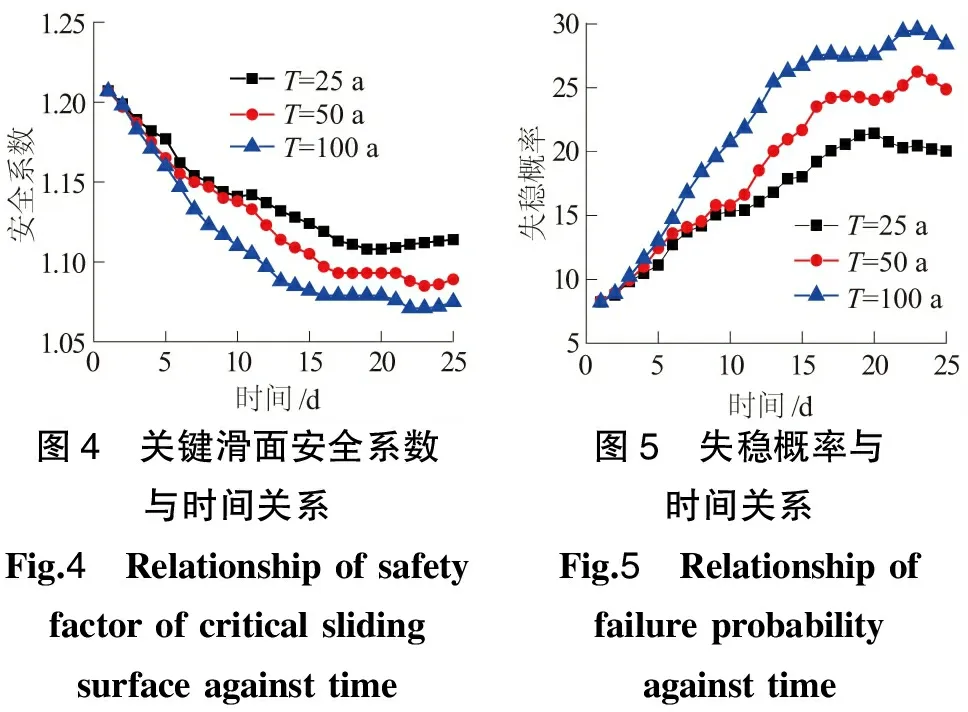
图4　关键滑面安全系数与时间关系Fig．4　Relationshipofsafetyfactorofcriticalslidingsurfaceagainsttime图5　失稳概率与时间关系Fig．5　Relationshipoffailureprobabilityagainsttime

从图4可看出降雨作用于斜坡具有明显的时间滞后效应。在降雨时程中，安全系数随时间增加而逐步减小。其原因在于：降雨入渗过程中，各时步的孔隙水压力分布不断变化，但最终随着入渗达到稳态，安全系数也会收敛于某一值。另一方面，如图5所示，随重现期的增加，总的降雨入渗量增加，对应的安全系数相应减小，而失稳概率总体呈增大趋势。

因此，本文故取渗流稳定后的最后时步时刻的稳定可靠度计算结果作为后续耦合计算的基础。本案例中，经过计算显示，降雨25 d之后入渗达到了稳态。同时，本文计算所得的斜坡失稳概率，采用徐卫亚等[28]所提的关于斜坡失稳破坏的危险性分级标准(表2)进行分级。

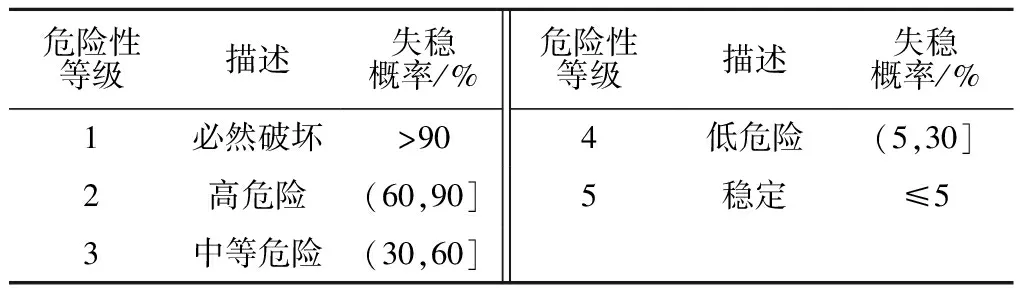
表2　斜坡失稳概率的危险性等级[28]Table 2　Failure probability and corresponding hazardlevel of deposit slope[28]

渗流稳定后斜坡的稳定性及危险性评价结果如表3所示，相比年均降雨情况，极端降雨作用下斜坡稳定性有部分的下降，安全系数最大降低了12%，失稳概率虽然仍保持在低危险性水平，但已十分接近中等危险性。但就不同重现期而言，斜坡的稳定性情况变化并不显著，安全系数变化幅度为3%，失稳概率也保持在同一量级。分析认为，就西藏流域而言，服从对数正态分布的最大3 d降雨量在不同重现期下差距不大，量值上仅相差约15 mm/d，但相对年均降雨水平相差较大。同时，由于SLOPE/W极限平衡计算中要求各条块的安全系数均相同，故不同降雨入渗量所带来的孔隙水压力分布的差异会被各个条块平均化。

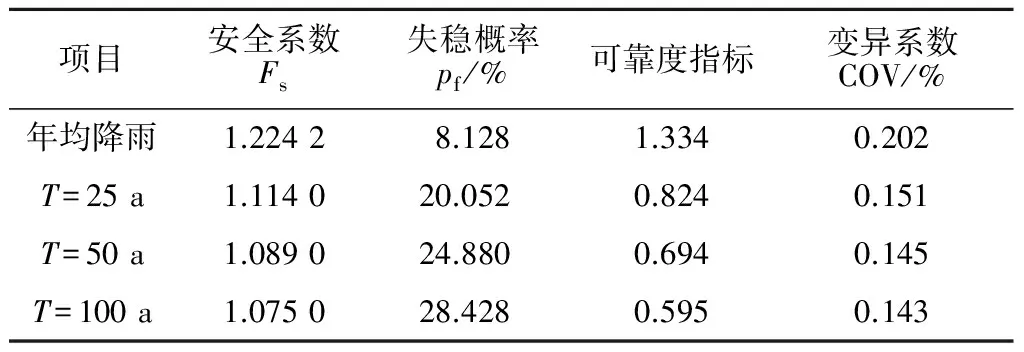
表3　降雨因素诱发滑坡失稳概率Table 3　Failure probability of rainfall-inducedlandslide

注：安全系数与失稳概率均为入渗稳定后的最后时步计算结果；以上结果基于5×104次MCS计算

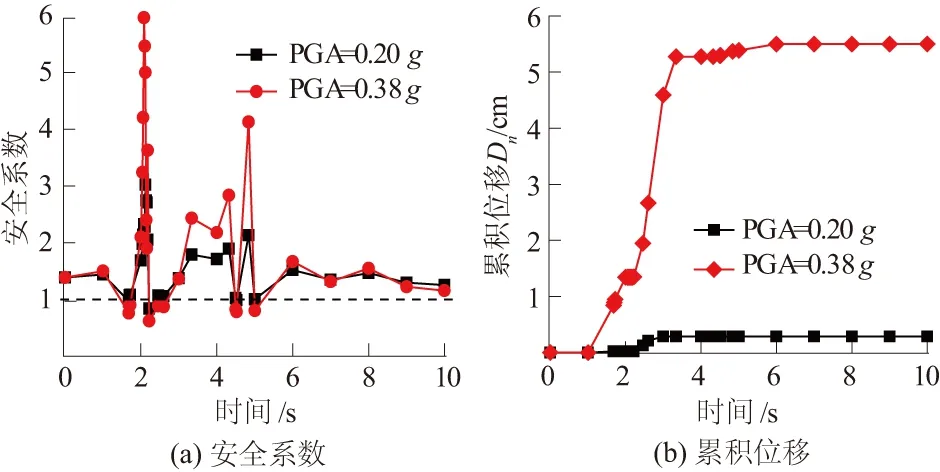
图6　地震作用下斜坡安全系数和累积位移时程曲线Fig.6　Time-history curves of safety factor of deposit slopeand cumulative displacement under earthquake action

3.2　地震诱发作用下的失稳概率

在考虑案例场地地震动参数的随机性时，参照中国地震动区划图所得到的概率地震危险性(PSHA)结果，选取地震动危险性等级为基本地震动(50 a超越概率10%)与罕遇地震动(50 a超越概率2%)。根据场地条件选取宝兴民治所记录的汶川地震波，并依据上述危险性等级进行幅值和时间压缩比的修正。

同时，为了充分说明斜坡在对应地震动量级下的动力响应，综合采用拟静力法、动力有限元法、Newmark法的结果进行对比分析。其中，通过采用QUAKE/W软件进行动力有限元分析，其结果如图6所示。值得注意的是，目前对累积位移阈值还没有形成统一的标准，大量研究根据各自区域的特点选取位移阈值，本文基于案例所在的藏东南地区与已有研究区域的相似性确定Dn=5 cm作为斜坡失稳的判别条件[29]。

基于Newmark位移法的计算结果如图7所示。图7(c)为不同震动等级下斜坡累积位移的危险性曲线，展示了在PGA=0.2g与PGA=0.38g两种地震动条件下，累积位移Dn的危险性分布(MCS次数均为5×104)。并最终将Newmark位移法的计算结果与动力有限元、拟静力法的结果汇总成为表4。

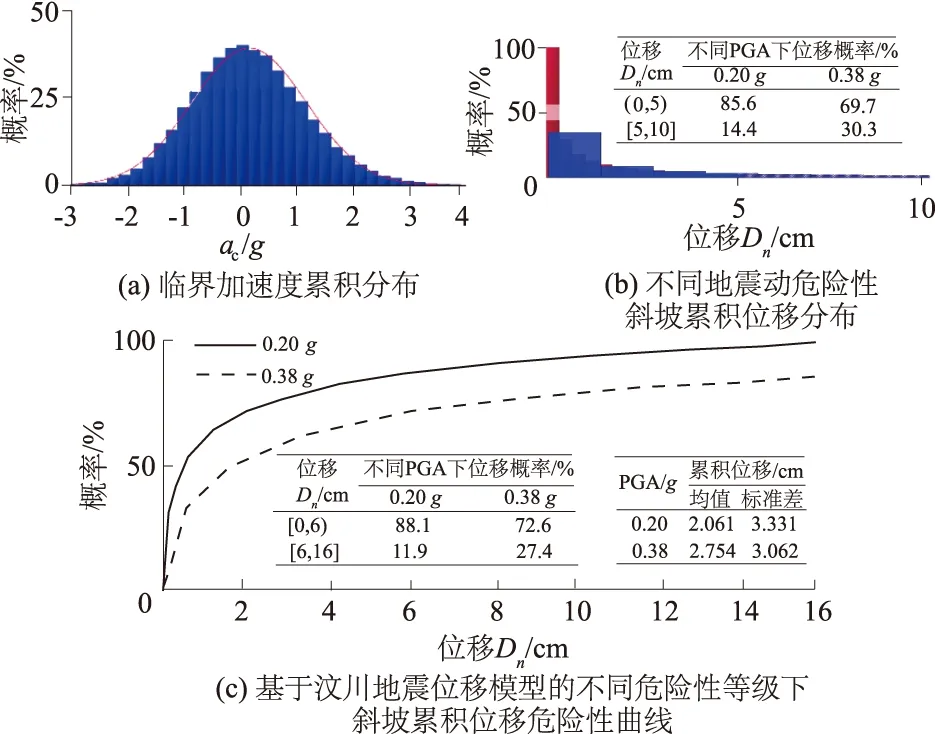
图7　基于Newmark位移法的计算结果Fig.7　Results of displacement calculated by Newmark’smethod

从安全系数的角度考虑，由QUAKE/W计算得到的安全系数时程曲线(图6(a))可以看出，在整个震动时程中只有少数时刻斜坡安全系数<1，总体呈现出稳定的趋势；且2种危险性等级下，斜坡的安全系数相差不大。从累积位移角度考虑，由表4可见，Newmark累积位移法同动力有限元法所得到的位移Dn结果较为接近。若从确定性的角度对累积位移结果同阈值进行比较，如表4及图6(b)所示，堆积体斜坡在罕遇地震动危险性等级，动力有限元法和Newmark法所得位移结果分别超过阈值的10%和1.4%，即2种方法所得位移值均没有显著超过阈值。因此，进一步从概率危险性的角度进行分析，依据表2的危险性分级标准，通过Newmark位移法计算得到的罕遇地震动条件下地震滑坡危险性为中等危险性(30.3%)，见图7(b)与表4所示；其失稳概率较基本地震动条件时显著提高，而基本地震动条件仅为低危险性(14.4%)。

另一方面，从表4可以看出，采用拟静力法得到的结果非常保守，无论是从安全系数还是失稳概率角度分析都几乎确定在罕遇地震动下会发生失稳。

表4　地震因素诱发滑坡失稳概率Table 4　Failure probability of earthquake-induced landslide

注：拟静力法计算结果基于5×104次MCS计算；动力有限元方法所得到的安全系数为地震时程的最后时刻的值

3.3　降雨地震耦合作用下的失稳概率

综上所述，根据工程案例的实际工程地质条件时，以前述不同重现期的最大3 d降雨量、不同危险性等级的地震动强度为例，通过式(1)可计算得降雨地震耦合作用下堆积体斜坡的年失稳概率，如表5所示。

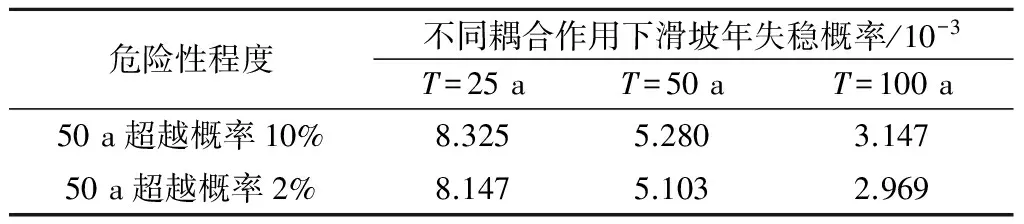
表5　不同危险性等级地震降雨因素耦合作用下滑坡年失稳概率Table 5　Annual failure probability of landslideunder the coupled action of earthquake andrainfall of different hazard levels

根据Fell等[9]基于年失稳概率的危险性分级，表5各种危险性组合下都为“中等危险性”(即年失稳概率10-3～10-4)。并且，由表5可以得出，随着极端事件自身危险性等级的提高，虽然其诱发概率有所提高，但同时由于越极端的事件其回归周期越长，发生概率越低，所以综合来讲，诱发事件组合越极端，其综合危险性反而越低。

4　结　论

本文分别考虑外界诱发因素自身的随机性与诱发作用过程的不确定性，通过分析不同量级诱发事件的发生概率与回归周期，结合蒙特卡罗模拟计算对应诱发事件作用下的斜坡失稳概率，揭示不同程度的滑坡危险性序列。在此基础上利用全概率公式进行多致灾因素的耦合计算，系统评价堆积体斜坡的危险性与潜在风险。此方法可以推广到多随机致灾因素耦合的情形。

将本文方法应用于川藏交通廊道沿线某典型堆积体斜坡，考虑不同危险性等级下的地震与降雨的耦合诱发作用。主要结论归纳如下：

(1)考虑降雨诱发作用的不确定性时，采用边坡非饱和渗流的数值模拟结合蒙特卡罗模拟的方法简单高效，案例分析的结果表明不同极端降雨作用下，危险性差距并不显著，均为低危险性，安全裕度不够充分。

(2)考虑地震诱发作用时，拟静力法结果显得十分保守，而动力有限元法与Newmark累积位移法的结果较为接近，显示出随地震动等级的增加，斜坡的失稳概率有较大的增加。

(3)耦合作用下案例堆积体斜坡年失稳概率为中等危险性，总的规律表现为诱发事件组合越极端，其综合危险性反而越低。因此，由于较多工程区域气候地质环境的复杂性而具备众多致灾因素，本文所采取耦合分析能够提供更为全面的参考与指导。

参考文献：

[1]刘盛健. 川藏公路地质灾害危险性评价[D]. 重庆：重庆交通大学, 2011.

[2]朱平一，何子文，汪阳春，等. 川藏公路典型山地灾害研究[M]. 成都: 成都科技大学出版社, 1999.

[3]廖秋林，李晓，董艳辉，等. 川藏公路林芝—八宿段地质灾害特征及形成机制初探[J]. 地质力学学报, 2004, 33(1): 33-39.

[4]何朋朋，姚磊华，周平根，等. 多随机因素条件下的峡口滑坡可靠性分析[J]. 岩土工程学报, 2010,32(6): 930-937.

[5]张璐璐，邓汉忠，张利民. 考虑渗流参数相关性的边坡可靠度研究[J]. 深圳大学学报(理工版), 2010, 27(1): 114-119.

[6]TUNG Y K，CHAN G C C. Stochastic Analysis of Slope Stability Considering Uncertainty of Soil-water Retention Characteristics[J]. Applications of Statistics and Probability in Civil Engineering, 2003, 1/2:1409-1414.

[7]蒋水华，李典庆，周创兵，等. 考虑参数空间变异性的非饱和土坡可靠度分析[J]. 岩土力学, 2014, 35(9): 2569-2578.

[8]王贺，张洁，陈飞扬. 强降雨条件下花岗岩残积土边坡的时变可靠度[J]. 武汉大学学报(工学版), 2016, 49(5): 763-767.

[9]FELL R，COROMINAS J，BONNARD C，etal. Guidelines for Landslide Susceptibility, Hazard and Risk Zoning for Land-use Planning[J]. Engineering Geology, 2008, 102(3): 99-111.

[10] 陈丽霞，殷坤龙，刘长春. 降雨重现期及其用于滑坡概率分析的探讨[J]. 工程地质学报, 2012, 20(5): 745-750.

[11] 鲍叶静，高孟潭，姜慧. 地震诱发滑坡的概率分析[J]. 岩石力学与工程学报, 2005, 24(1): 66-70.

[12] DAI F C，LEE C F，NGAI Y Y. Landslide Risk Assessment and Management: An Overview[J]. Engineering Geology, 2002, 64(1): 65-87.

[13] 黄润秋. 20世纪以来中国的大型滑坡及其发生机制[J]. 岩石力学与工程学报, 2007, 26(3): 433-454.

[14] 黄润秋，戚国庆. 非饱和渗流基质吸力对边坡稳定性的影响[J]. 工程地质学报, 2002, 10(4): 343-348.

[15] FREDLUND D G, XING A, HUANG S. Predicting the Permeability Function for Unsaturated Soils Using the Soil-Water Characteristic Curve[J]. Canadian Geotechnical Journal, 1994, 31(4), 533-546.

[16] 王涛，吴树仁，石菊松，等. 地震滑坡危险性概念和基于力学模型的评估方法探讨[J]. 工程地质学报, 2015, 23(1): 93-104.

[17] JIBSON R W. Methods for Assessing the Stability of Slopes during Earthquakes—A Retrospective[J]. Engineering Geology, 2011, 122(1/2): 43-50.

[18] 徐光兴，姚令侃，李朝红，等. 边坡地震动力响应规律及地震动参数影响研究[J]. 岩土工程学报, 2008, 30(6): 918-923.

[19] JIBSON R. Predicting Earthquake-induced Landslide Displacements Using Newmark’s Sliding Block Analysis[J]. Transportation Research Record, 1993, (1411):9-17.

[20] AMBRASEYS N N，MENU J M. Earthquake-induced Ground Displacements[J]. Earthquake Engineering & Structural Dynamics, 1988, 16(7): 985-1006.

[21] JIBSON R W. Regression Models for Estimating Coseismic Landslide Displacement[J]. Engineering Geology, 2007, 91(2): 209-218.

[22] RATHJE E M，SAYGILI G. Probabilistic Seismic Hazard Analysis for the Sliding Displacement of Slopes: Scalar and Vector Approaches[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2008, 134(6): 804-814.

[23] RATHJE E M，SAYGILI G. Probabilistic Assessment of Earthquake-induced Sliding Displacements of Natural Slopes[J]. Bulletin of the New Zealand Society for Earthquake Engineering, 2009, 42(1): 18-27.

[24] RATHJE E M，SAYGILI G. Estimating Fully Probabilistic Seismic Sliding Displacements of Slopes from a Pseudoprobabilistic Approach[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(3): 208-217.

[25] REFICE A，CAPOLONGO D. Probabilistic Modeling of Uncertainties in Earthquake-induced Landslide Hazard Assessment[J]. Computers & Geosciences, 2002, 28(6): 735-749.

[26] 陈语，李天斌，魏永幸，等. 沟谷型滑坡灾害链成灾机制及堵江危险性判别方法[J]. 岩石力学与工程学报, 2016, 35(增2): 4073-4081.

[27] 张玉虎，王琛茜，刘凯利，等. 不同概率分布函数降雨极值的适用性分析[J]. 地理科学,2015,35(11): 1460-1467.

[28] 徐卫亚, 张志腾. 滑坡失稳破坏概率及可靠度研究[J]. 灾害学, 1995,(4):33-37.

[29] JIBSON R W，HARP E L，MICHAEL J A. A Method for Producing Digital Probabilistic Seismic Landslide Hazard Maps[J]. Engineering Geology, 2000, 58(3): 271-289.