Dwell Scheduling Algorithm for Digital Array Radar
Qun Zhang, Di Meng,, Ying Luo and Yijun Chen
(1.Institute of Information and Navigation, Air Force Engineering University, Xi’an 710077, China; 2.Collaborative Innovation Center of Information Sensing and Understanding, Xi’an 710077, China)
With the improvement of radar digitization,digital array radar (DAR) has been widely researched in the radar industry[1]. Compared with traditional analog phased array radar, DAR not only has the advantages of high detection precision, complex target detection capability, and strong anti-jamming capability, but also has the characteristics of flexible signal processing mode. It can be used to search a number of airspaces, and track and image multiple targets simultaneously—resulting in effective time resource management of radar[2].
Reasonable, flexible and effective scheduling strategies are the key to exploiting the high adaptive potential of DAR. Among existing studies, there are mainly two ways to implement resource management of DAR: template-based scheduling and adaptive scheduling. Adaptive scheduling methods flexibly adjust the resource scheduling strategy according to the working environment and task requirements, and are the most effective but also the most complex scheduling methods[3].
So far, many scholars have studied the radar resource scheduling model. In Ref.[4], an adaptive algorithm of phased array radar based on time window is proposed to verify the rationality and validity of introducing time window in the scheduling process. A resource allocation model based on “Quality of Service” is proposed in Ref.[5] to optimize the target tracking performance of phased array radar systems. In Ref.[6], an adaptive scheduling algorithm based on information entropy is proposed to solve the optimal searching problem in target regions. In order to further improve the source utilization ratio of the radar system and give full play to the advantages of multifunction digital array radar, pulse interleaving technology is proposed. Its core idea is to schedule the transmission or reception pulse of other tasks in a single task pulse interval. Orman analyzed this method in Ref.[7] and proposed a heuristic algorithm to solve the problem of adaptive beam-dwell scheduling for phased array radar. In Ref.[8], an optimal algorithm based on pulse interleaving for radar task quadratic programming model is proposed to improve the scheduling success ratio of tasks with high priority. Aiming at the problem of beam-dwell scheduling for DAR, an algorithm based on analyzing scheduling interval is proposed in Ref.[9]. However, in almost all existing adaptive resource scheduling methods for DAR, the imaging mission is not taken into account. Joint scheduling imaging tasks with search, tracking and other tasks not only improve the recognition ability of the radar to the target and give full play to the advantages of multi-task cooperation, but also feedback the target characteristic information obtained by the image to the transmitter radar system.This enables the realization of dynamic adjustment of imaging tasks and improves the resource utilization ratio[10]. Traditional imaging algorithms require continuous observation of targets for a long time to obtain high-resolution images, but the alternation of different tasks inevitably leads to discontinuous synthetic aperture sampling of the imaging target azimuth.
Based on the above issues, in this paper we propose a dwell scheduling algorithm for DAR, which takes the imaging task requirements into account in the radar resource scheduling model, by using the compressed sensing (CS) ISAR imaging method.
1 Task Model and Constraints Based on Pulse Interleaving
DAR is a kind of all-digital phased array radar, which can receive and transmit the beam in a digital way. It can be interleaved in the form as shown in Fig.1.txj,twj,trjdenote the radar beam transmitting duration, waiting duration of a dwell, and the radar beam receiving duration respectively forj(j=1,2).With the pulse interleaving technology in DAR, time resources of the waiting duration can transmit or receive other resident tasks,and furthermore, the receiving duration of dwell tasks can overlap each other at the same time.

Fig.1 Form of pulse interleaving in DAR
1.1 Sparse aperture imaging based on compressed sensing
The traditional DAR needs to separate part of the continuous time resources to achieve imaging capabilities in the implementation of the target searching and tracking, which leads to the contradiction of the radar resource allocation and low radar efficiency. Under the framework of CS theory, continuous observation of the target image can be transformed into random sparse observation, and high-quality target ISAR image can be obtained under sparse aperture condition. This provides an effective technical support for incorporating imaging task requirements into the DAR resource scheduling model.
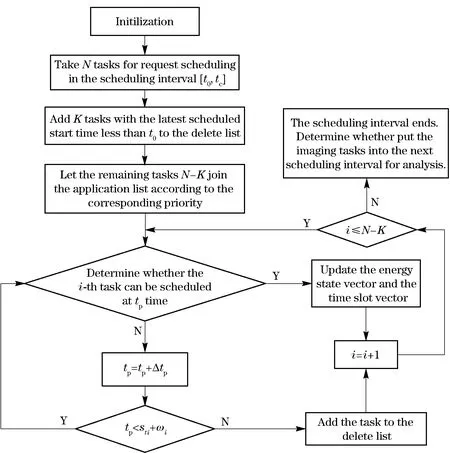
In order to improve the adaptive ability of radar imaging, the method proposed in Ref.[10] can be used to recognize the characteristics of the targets after entering the stable tracking phase, and then calculate the demand of radar resources for target imaging based on the cognitive results. We estimate the distancei, speedi, headingi, target sizei, sparsity of echo in Doppler domainiand observation timeciof thei-th target. Assuming that the target is non-maneuvering, the full aperture imaging of the radar needs to transmitNi=Pfcipulses (Pfis the pulse repetition frequency), and the measurement dimensionMi(Mi Mi≥cilnNi (1) wherecis a constant associated with the recovery accuracy, usually taken as 0.5-2(we assumec=1 in this paper). The DAR dwell model is defined as T={et,st,tx,tw,tr,ω,M,pri,Pt,P} (2) whereetdenotes the expected scheduling time;stdenotes the actual scheduling time;tx,tw,trdenote the transmitting duration, waiting duration and receiving duration respectively;ωdenotes the time window of the task;Mdenotes the number of pulse repetitions in the search and tracking tasks, and denotes the azimuth-oriented observation dimension in the imaging task; pri denotes the pulse repetition reputation interval;Ptdenotes the pulse transmitting power; andPdenotes the task priority[13]. For tracking and imaging tasks, assuming the distance from theith target to the radar isi, the waiting duration for theith task dwell can be calculated from the predicted position information of the target, which is given by twi=2i/c (3) For the search tasks, it is generally impossible to obtain the arrival time of the echo in the absence of prior information. Therefore, in order to ensure that radar echo signals can be effectively received after the searching pulse is transmitted, once the transmitting duration ends, the antenna system must be in the receiving state until the maximum waiting time, i.e. the waiting duration of the search task dwell cannot be preempted. It should be noted that the arrival time of radar echo is affected by the range size of the target.In order to ensure the imaging quality, the received pulse should be broadened properly. Suppose that the distance from thei-t target to the radar isiand the range size of the target isyi, the width of the actual received pulse of theith imaging task can be expressed as twi=2(i+yi)/c (4) Although the overlap of multiple dwell tasks can improve the resource utilization of DAR, the energy consumption of the system is bound to increase as the radar is in the transmitting state for a long time. In order to avoid the damage of the transmitter due to the long working time, the restriction of energy constraint must be considered in the scheduling algorithm. The transient energy of the system attmoment can be expressed as (5) whereP(x) is the power parameter, andτis the look-back period, which is related to the heat transfer of the system. The energy constraint of the system can be defined as thatE(t) cannot exceed the maximum thresholdEmaxof instantaneous energy at any time, i.e. E(t)≤Emax (6) which meansE(t) cannot exceed the maximum thresholdEmaxof instantaneous energy at any time. In simulation, the energy consumption of radar beam and the variation of energy state in time Δtcan be estimated in prior by the parameters of antenna gain, transmission power, pulse width and pulse number, so as to reduce the complexity of algorithm. Without loss of generality, the target at a closer distance, higher speed and moving toward the radar is more threatening and requires a higher priority for tracking and imaging. If the tracking is divided into precision tracking and normal tracking, theith priority of the precision tracking task and the normal tracking task is defined as (7) (8) We divided the search task into high priority search (with priority of 3) and low priority search (with priority of 1). We assume only one verification beam is transmitted for confirmation after searching for a new target. Then the new target is added to the existing tracking task list to recognize the feature, calculate the tracking priority, and scheduled within the next scheduling interval. When a precise tracking task enters the stable tracking phase (assume radar enters the stable tracking phase after transmittinglibeam to track), the strategy of tracking and imaging are adopted at the same time in the next scheduling interval. The priority of theith imaging task that enters the stable tracking phase is defined as (9) Obviously, the priority of the imaging task is between 0 and 1, which is ensured to be lower than the priority of search and tracking tasks. The scheduling of an imaging task usually takes several scheduling intervals, in order to ensure that the pulses transmitted by the radar are not wasted during the imaging process, and a priority dynamic adjustment strategy is adopted for imaging tasks. Ifith imaging task is implemented in thekth scheduling interval, the priority of theith imaging task should be increased appropriately when allocating resources to the next scheduling interval. Pi,k+1=Pi,k+ΔP (10) where ΔPis the step value of priority. In order to make better use of the time resources of DAR to image as many precise tracking targets as possible, we propose the self-adaptive adjustment strategy of the imaging accumulation time of different imaging targets. After the end of each scheduling interval, the ISAR image of the target is reconstructed by using all of the previous observed sub-pulses up to the scheduling interval. Generally, as the imaging accumulation time increases, the quality of ISAR images increase accordingly and gradually come to a standstill. After reaching the standstill, the quality of ISAR image become worse if the imaging accumulation time continues to increase. Therefore, the mutual information can be taken as the similarity measure of adjacent reconstructed ISAR image. Mutual information represents the amount of information that two images contain about each other. For adjacent reconstructed imagesAandB, their mutual informationI(A,B) is expressed as (11) wherepi,pjdenote the gray probability distribution ofAandBrespectively, andpijdenotes the joint gray probability distribution. The larger the valueI(A,B) is, the higher the similarity of the two structure image is. After selecting an appropriate thresholdTαby reference to the desired resolution, if the mutual information of the target ISAR image obtained after the two adjacent scheduling intervals is less than the thresholdTα, continue to analyze the imaging task in the next scheduling interval.If the mutual information is more than the thresholdTα, it is considered that the imaging quality of target is up to the expected standard, and the imaging task is finished. In order to measure the performance of the radar resource scheduling, the scheduling success ratio (SSR), the hit value ratio (HVR), the time utilization ratio (TUR) and the energy utilization radio (EUR) are taken as the criterion. They can be expressed as SSR=N′/N (12) (13) (14) (15) whereNis the total number of tasks for requested scheduling,N′ is the number of scheduled tasks,Ttis total simulation time,Ptis the peak power of each transmitted pulse andPavis the average power delivered by the radar. In terms of the above performance index, assume that there areNdwell tasks in the scheduling interval [t0,te], an effective model of DAR based on pulse interleaving can be defined as (16) whereN′ is the number of search tasks andq1,q2,q3,q4are adjustment factors. The first constraint gives the scope of the actual execution time of each task; the second constraint indicates that there is no conflict between the transmitted pulses, i.e. the transmitting duration of the radar task cannot be preempted; the third constraint indicates that the search tasks cannot perform pulse interleaving; the fourth constraint indicates that the task dwell received pulse can be overlapped in the same time without colliding with the transmitted pulse; and the fifth constraint represents the energy constraint for task scheduling. The nonlinear programming problem in Eq.(16) is an N-P problem, and it is difficult to obtain the optimal solution. As a consequence, heuristic algorithms are usually used to obtain sub-optimal solutions[16]. With the self-adaptive adjustment strategy based on pulse interleaving, a heuristic method for solving the optimization problem is given. The effective algorithm of DAR based on pulse interleaving is summarized as follows. D= te-t0Δt , Step1TakeNtasks for requested scheduling in the scheduling interval [t0,te], addKtasks with the latest scheduled start time less thant0to the delete list, discretize the system time; suppose that the length of each time slot is Δt, the number of time slot is introduce time pointertp=t0, initialize the time slot vector U={u1,u2,…uD}=0 and energy state vector E. Step2Let the remainingN-Ktasks join the application list according to the corresponding priority from high to low (tasks with the same priority are arranged according to the expected execution time), and leti=1. Step3Determine whether theith task can be scheduled at timetp. If the task meets the time and energy constraints in Eq.(16), it will be sent to the execution list and removed from the application list. The time slot vector U and time pointertpcan be rewritten as follows. Case 1: Search tasks uk=1,k∈( stiΔt , sti+txi+twi+triΔt ) (17) tp=sti+txi+twi+tri (18) Case 2: Tracking tasks uk=2,k∈ (19) tp=sti+txi (20) Case 3: Imaging tasks uk=3,k∈( stΔt , sti+txi+twi+triΔt ) (21) tp=sti+txi (22) In order to distinguish different task types, the time slotsukare assigned 1, 2 and 3 respectively. Update the energy state vector E=E+ΔE(ΔE is the system energy consumption change), leti=i+1, and return to step 3. If the scheduling fails, adjust the actual execution time of the task in the time window, and lettp=tp+Δtp(Δtpis the minimum step size of the pointer slide). Step4Iftp Step5Ifi≤N-K, return to step 3, otherwise go to step 6. Step6The scheduling analysis of the scheduling interval ends. Use the sparse-aperture ISAR imaging method for target imaging by using all of the previously observed sub-pulses up to this scheduling interval. When the mutual information is more than the predefined threshold, this imaging task is no longer scheduled in the next scheduling interval. Otherwise, put the imaging task into the next scheduling interval for analysis. The flow chart of the scheduling process in one scheduling interval is as shown in Fig.2. Fig.2 Flow chart of the scheduling process In the simulation, we choose three kinds of radar working mode: search, tracking and imaging. Typical parameters for various tasks are summarized in Tab. 1. The total simulation time was 6 s, the scheduling interval length was 50 ms, and the radar can provide an average power of 400 W. For search and tracking tasks, radar transmits narrowband signals, center frequencyfc=10 GHz, signal bandwidthB=10 MHz, and pulse repetition frequencyPf=1 000 Hz. For imaging tasks, radar transmits LFM signals, center frequencyfc=10 GHz, signal bandwidthB=300 MHz, pulse repetition frequencyPf=1 000 Hz, and priority sliding step ΔP=0.1. Tab.1 Parameters of radar tasks Traditional phased array radar algorithm (traditional algorithm)[15], the pulse interleaving scheduling algorithm(simple task algorithm) which does not consider the imaging tasks[9]and the adaptive dwell scheduling algorithm proposed in this paper (proposed algorithm) are compared in the simulation. Comparison curves of three different algorithms are shown in Tab.2-Tab.5. Tab.2 Scheduling success ratio % Tab.3 Hit value ratio % Tab.4 Time utilization ratio % Tab.5 Energy utilization ratio % From Tab.2, we see that when the number of tasks is 20, system resources are relatively abundant and the competition for resources among tasks is not obvious. All the three scheduling algorithms can successfully schedule all tasks. With the further increase of the tasks, the scheduling success radio of the traditional algorithm begins to decline significantly, while the other two algorithms based on the pulse interleaving can still successfully schedule all tasks. When the number of tasks increased to 60, the simple task algorithm cannot schedule more tasks, but the proposed algorithm can successfully schedule all tasks.This is due to the saturation of radar resources in the simple task algorithm.In the proposed algorithm, the imaging tasks have the lowest priority, so the remaining resources of the system can be fully utilized by the dynamic adjustment of the imaging accumulation time and the flexible sparse aperture allocation, without affecting the scheduling of the search and tracking tasks. Consequently, the task number of successful scheduling is improved. From Tab.3, we see that when the number of tasks is 20, the system resources are relatively abundant; but when the number of tasks increased to 40, the hit value ratio of traditional algorithm has fallen to a great extent. The precision tracking task can be imaged with the idle time of searching and tracking in proposed algorithm, so that it maintains a high hit value radio when the number of tasks reaches 80. From Tab.4 and Tab.5, we see that when the number of tasks is 20, the time utilization ratio and the energy utilization ratio plateau at 0.1 because of the resource bottleneck in traditional algorithm. Through the use of the pulse interleaving technology, the simple task algorithm can further utilize the radar system resources, the time utilization ratio can reach about 0.57 and energy utilization can reach about 0.5. On the basis of pulse interleaving, the idle time of search and tracking task is fully exploited in the proposed algorithm, so the time utilization ratio and energy utilization ratio can reach about 0.75 and 0.6 respectively. In order to validate that the DAR can achieve the target imaging while searching and tracking, the imaging results of three imaging tasks above are compared with the traditional full aperture ISAR imaging results, and the peak signal to noise ratio (PSNR) is used to measure the effect of the proposed algorithm. The PSNR is defined as (23) whereσ(i,j) denotes the sparse aperture imaging result in this paper,σ(i,j) denotes the traditional full aperture imaging result,mandndenote the number of rows and columns of the ISAR image matrix respectively. The larger the PSNR value, the better the imaging effect. The contrast between the traditional full aperture imaging and the sparse aperture imaging in this paper is shown in Tab.6. From Tab.6, it is shown that the proposed imaging method can be used to solve the problem of azimuth aperture sparsity and obtain satisfactory image quality. Tab.6Comparison of the image quality by the conventional full aperture and the sparse aperture In this paper, a dwell scheduling algorithm has been proposed based on pulse interleaving for DAR. The time and energy constraints are set respectively, and the optimal resource scheduling algorithm is established. The simulation results show that the proposed algorithm can accomplish tracking and search task effectively as well as obtain high quality sparse aperture ISAR image. It not only makes use of the multi-task cooperative advantage of DAR, but also improves the resource utilization ratio of radar system. It should be noted that, in this paper, we assume that the target is non-maneuvering and the maneuverability of the target in the actual imaging process is ignored. For the target imaging of maneuvering flight, in addition to the sparsity of the azimuthal aperture, the optimal imaging time and the quality evaluation criteria of the imaging should be considered. Related content should be further studied. [1] Wang Feng, Fu Youguang. Performance comparison of digital phased array and conventional phased array radar[J]. Journal of CAEIT, 2012, 7(2): 148-151. (in Chinese) [2] Cheng Ting, He Zishu, Li Huiyong. An adaptive dwell scheduling algorithm for digital array radar[J]. Acta Electronica Sinica, 2009, 37(9): 2025-2029. (in Chinese) [3] Komorniczak W. Pietrasinski[J]. Selected problems of MFR resources management[C]∥The 3rd International Conference on Information Fusion, Paris, France, July 10-13, 2000. [4] Jang D S, Choi H L, Roh J E. A time-window-based task scheduling approach for multi-function phased array radars[C]∥IEEE International Conference on Control, Automation and Systems, Gyeonggi-do, South Korea, Oct. 26-29, 2011. [5] Lee C G, Kang P S, Shi C S, et al. Radar dwell scheduling considering physical characteristics of phased array antenna[C]∥Proceedings of the 24th IEEE International Real-Time Systems Symposium(RTSS’03), Cancun, Mexico, Dec 5, 2003. [6] Zhang Juan, Xia Zhongting. An adaptive scheduling searching method based on information entropy[J]. Modern Radar, 2015, 37(8): 33-36. (in Chinese) [7] Orman A J, Potts C N, Shahani A K. Scheduling for a multifunction phased array radar system[J]. European Journal of Operational Research,1996,90(1):13-25. [8] Zhao Yu, Li Jianxun, Cao Yinglan, et al, Adaptive scheduling algorithm based on quadratic programming for multifunction phased array radars[J]. Systems Engineering and Electronics, 2012,34: 698-703. (in Chinese) [9] Cheng Ting, He Zishu. Novel radar dwell scheduling algorithm based on pulse interleaving[J]. Journal of Systems Engineering and Electronics, 2009, 20(2): 247-253. (in Chinese) [10] Chen Yijun, Zhang Qun, Luo Ying, et al. Adaptive scheduling algorithm for radar based on sparse aperture ISAR imaging[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2013, 33(4): 171-176. (in Chinese) [11] Li Wenjing, Chen Hongwei. A kind of ISAR imaging algorithm based on compressed sensing[J]. Computer Simulation, 2015, 32(8): 10-13. (in Chinese) [12] Chen Y J, Zhang Q, Luo Y, et al. Measurement matrix optimization for ISAR sparse imaging based on genetic algorithm[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(12):1875-1879. [13] Chen J, Wang L, Zhang W, et al. Multifunction phased radar resource management via maximal pulse interleaving technique[J]. Arabian Journal for Science and Engineering, 2013, 38(11): 3081-3091. [14] Hou Q K, Liu Y, Fan L J, et al. Compressed sensing digital receiver and orthogonal reconstructing algorithm for wideband ISAR radar[J]. Science China Information Sciences, 2015, 58(2):1-10. [15] Wang Qiang, Xu Jungang, Wang Hongan, et al. A new priority table based real-time scheduling algorithm[J]. Acta Electronica Sinica, 2004, 32(2): 310-313. (in Chinese) [16] Focke R W, Villiers J P D, Inggs M R. Interval algebra-An effective means of scheduling surveillance radar networks[J]. Information Fusion, 2015, 23(3):81-98.1.2 Radar dwell model
1.3 Scheduling constraints

2 Dwell Scheduling Algorithm for DAR
2.1 Design of task priority
2.2 Adaptive adjustment of imaging accumulation time
2.3 Dwell scheduling algorithm

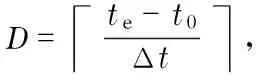
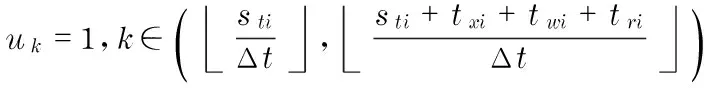
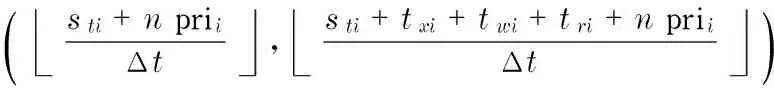

3 Simulation and Analysis






4 Conclusion
 Journal of Beijing Institute of Technology2018年1期
Journal of Beijing Institute of Technology2018年1期
