黄河上游茨哈峡水电站4#倾倒体稳定性研究

安晓凡, 李　宁,2

(1.西安理工大学 岩土工程研究所, 陕西 西安 710048; 2.兰州交通大学 土木工程学院, 甘肃 兰州 730070)

伴随着我国水电站工程建设的发展,与其相关的边坡工程对于水电站的安全施工和运行引起研究人员的广泛关注。水电边坡往往呈现出高、陡以及地质构造复杂的特征,边坡的稳定性和致灾程度则主要受控于工程开挖、蓄水及渗透、泄洪雨雾等人为因素,特别是水的影响[1-2]。水电边坡与其他工程(公路、铁路、矿山等)边坡的最大差别是有无库水的影响,因此研究这类边坡在与水相关的特定工况下的稳定性显得尤为重要。

何满潮等[3]按透水特性的不同将边坡岩体分为透水体介质、隔水体介质和复合型介质,并分别讨论了各介质的水力学作用方法。刘才华等[4]给出了考虑地下水影响的边坡极限平衡计算方法。库水位变化对岸坡的稳定性产生直接影响,一些学者运用不同方法展开研究。郭志华[5]、廖红建[6]、梁学战[7]通过渗流计算研究库水位变化和渗透系数对边坡安全系数的影响。朱冬林等[8]基于实测资料预测滑坡在库水位上升或下降的过程中,其稳定性表现出先减小后增大的过程。董金玉等[9]考虑堆积体与基岩接触带介质的应变软化,利用FLAC3D分析库岸边坡的变形破坏特征。刘晓丽等[10]将非连续变形分析(DDA)方法与离散裂隙网格(DNF)结合起来,提出一种用于研究渗流——应力共同作用下裂隙岩体的变形破坏特征的耦合模型。李邵军等[11]基于离心模型试验,模拟库区边坡在水位升降作用下的失稳过程。李卓等[12]研制了降雨与库水位共同作用下库岸边坡室内模型试验装置,对近坝库岸边坡进行了模型试验。

本文从分析地下水对岩质高边坡的影响机理入手,以茨哈峡水电站4#倾倒体为例,详细剖析其工程地质条件。运用离散化的有限元方法分析水荷载作用下边坡的变形特征,预测4#倾倒体在工程运行期可能发生的破坏模式。

1　地下水对岩质高边坡影响机理

地下水对库岸岩质边坡稳定性的影响主要表现为降雨和库水位变化两个方面。

1.1　降雨作用

降雨入渗对边坡岩体的影响主要表现为:雨水对岩体的物理、化学作用和降雨入渗产生的力学效应。

雨水通过地表入渗到坡内抬高地下水位,使滑动带岩土体发生饱水软化,导致抗剪强度降低并促使滑移变形加剧。因此滑动带岩土体的特性决定了降雨对坡体变形的影响程度。

层状岩质边坡的岩体强度主要由结构面控制,结构面在雨水条件下的物理性状改变明显,从而极大地降低了整个岩体的强度。同时,雨水的溶蚀作用也可能降低岩体的强度。在数值计算中,需要结合地质情况分析坡体不同类型岩石的软化系数,综合考量对自然状态下岩体强度参数的折减。例如:泥岩、页岩的软化系数可能小于0.5,甚至更低。

雨水在岩质边坡内的渗透路径通常沿结构面,渗流对岩体产生的力学作用表现为渗透压力。如果坡体内结构面不贯通或长时间的强降雨导致岩体内部雨水无法顺利排出,降雨入渗所产生的力学效应表现为雨水在结构面中的孔隙水压力。这种力学作用对边坡的稳定往往是不利的,尤其是存在密集的、交错的或者反倾向的结构面。

降雨对岩体的物理化学作用是不可逆的,而其力学效应是可逆的。本文通过对结构面岩土体的软化(折减抗剪强度参数),以及考虑雨水在结构面中产生的孔隙水压力(按照静水压力处理)两方面,模拟降雨条件下边坡的受力变形特征。

1.2　库水位变化

库水位升降过程中,岩体尤其裂隙发育的软弱岩体受到水的扰动,强度普遍降低,且吸水性越强,强度降低越大。同时坡体内部的软弱夹层、结构面、松散堆积体和基岩接触带岩体,受水浸泡时抗剪强度也会大幅度降低。此外,库水位周期性的变化过程中,地下水渗流对边坡岩体及滑面产生溶滤作用,使岩体及滑面的矿物成分发生变化,从而对岩土体的物理力学性质产生影响。

库水位上升对边坡岩体产生的力学效应主要表现为浮托力。浮托力对边坡的稳定性有正反两方面的影响:一方面,库水位上升导致坡体浸水体积增加,而且滑面上的有效应力减小使抗滑阻力减小,岩体饱水后部分滑体强度下降,对边坡稳定性产生不利影响;另一方面,浮托力使得滑体的有效重量减少,从而导致滑体的下滑力减小,反而有助于坡体的稳定。因此,对于库水位上升的影响不能一概而论,应针对具体工程的地质条件和岩体力学参数具体对待。数值计算中,浮托力的大小按公式(1)考虑。

F=γwAw

(1)

式中:γw为水的重度;Aw为浸润线以下滑体饱水面积。

库水位骤降对岩土体产生的力学效应主要表现为水头差产生的渗透压力。不同的渗透系数、浸润线形状、岩土体饱水面积所产生的渗透压力对坡体稳定性的影响都不尽相同。

因此,数值仿真分析中将水位以下岩体的抗剪强度值进行折减,容重采用浮容重。水位骤降时,通过在地下水位以下的岩体上施加体积力来模拟水对边坡产生的渗透力,即动水压力。本文采用平均水力坡降计算渗透力,平均水力坡降为浸润线与滑体交点间连线的坡比,即图1中的AB的斜率,滑体内部的总渗透力T为:

T=γwAwI

(2)

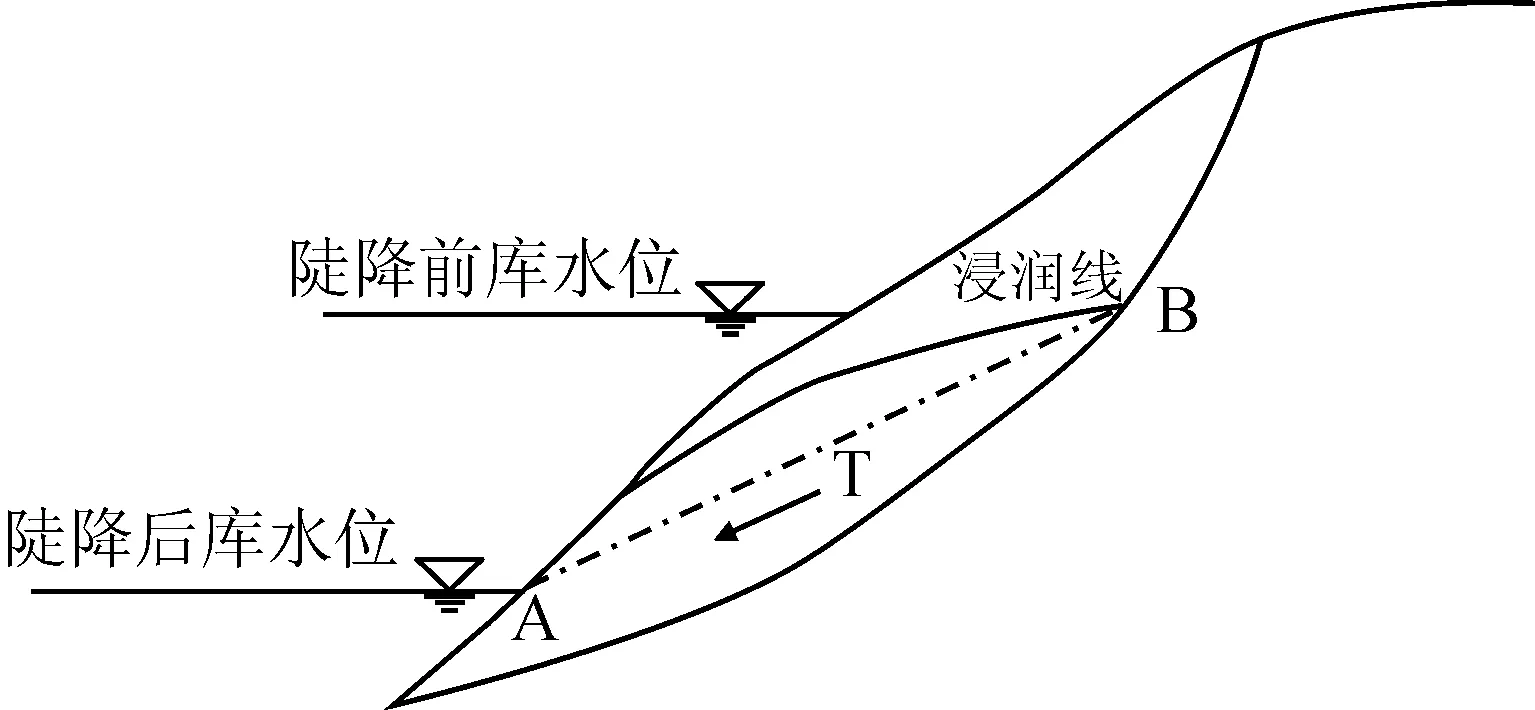
图1　边坡水力坡降示意图Fig.1　Schematic diagram of hydraulic gradient

式中I为平均水力坡降。渗透力的作用方向沿平均水力坡降方向。本文在数值模拟分析中从简化和安全的角度考虑,认为坡体的浸润线为坡面线。然后再将渗透力分解到水平和铅垂两个方向以体积力的方式施加到滑体上,构建渗流——应力耦合数值分析。

2　工程地质特征

2.1　工程概况

拟建的茨哈峡水电站位于青海省海南州兴海县与同德县交界处的茨哈峡峡谷,4#倾倒体位于大坝上游、黄河左岸。倾倒体前缘位于黄河水位以上,高程在2 785 m左右;倾倒体后缘位于左岸边坡顶部,高程在3 050～3 100 m之间,整个倾倒体边坡垂直高差在300 m左右,顺黄河方向长近千米。在倾倒体中部发育多条规模不等的冲沟。整体地貌特征、倾倒体边界及勘探洞位置见图2。

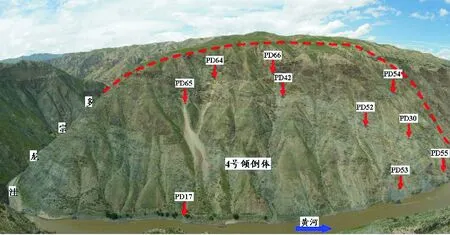
图2　4#倾倒体地形地貌特征Fig.2　Topography features of 4# toppling mass

该边坡地层主要为三迭系中统第三岩组的一套巨厚的浅变质砂、泥质碎屑岩组成,岩性为薄层灰色板岩与灰绿色砂岩互层、局部为中～薄层砂岩夹板岩。在斜坡中上部出露少量印支期中酸性侵入岩脉(γ5)和第三系上新统(N2)地层,在斜坡顶部为第四系覆盖。岩性统计结果:板岩占约48.5%,砂岩占约43.1%,砂板岩互层占约8.4%。

2.2　变形特征分析

4#倾倒体顺河流方向长度大,边坡的反倾层状岩体存在偏向上游侧倾倒变形的趋势,由于历时长因而变形程度明显且差异性较大。勘探平硐资料显示,坡体内部浅层岩体受不同程度倾倒变形以及风化卸荷的影响,大部分岩体拉裂、破碎成碎块状,稳定性较差,多处发生小规模的垮塌变形。

除了表部发育多条冲沟以外,总体来说,该边坡地形较为整齐,只有局部在暴雨情况下有小规模的滑动垮塌,整个边坡并无明显的大规模变形破坏迹象。坡顶地形平缓,无拉裂缝发育,表明目前左岸4#倾倒体稳定性较好。但是边坡在施工开挖卸荷、后期库水位上升(骤降)、暴雨等外荷载下,可能存在倾倒失稳的可能。

见图3,平硐内部岩体普遍拉裂变形,拉张裂隙张开宽度最大超过1 m,可以看到明显的岩层折断面,岩层产状由NE55°NW∠70°～80°转向NE55°NW∠35°～50°,但是未能观察到明显的滑动面。

图3　PD54号平硐30 m处岩体呈碎裂-散体状Fig.3　Fragmented rock mass at 30 m of PD54

以平洞和钻孔中岩体倾倒深度为基础,各剖面不同高程岩体倾倒水平深度见表1。总体来说,边坡岩体的倾倒水平深度在70 m到160 m之间,并且随着斜坡高程的增加,岩体的倾倒水平深度也逐渐增大,下游侧岩体的水平倾倒深度略大于上游侧。

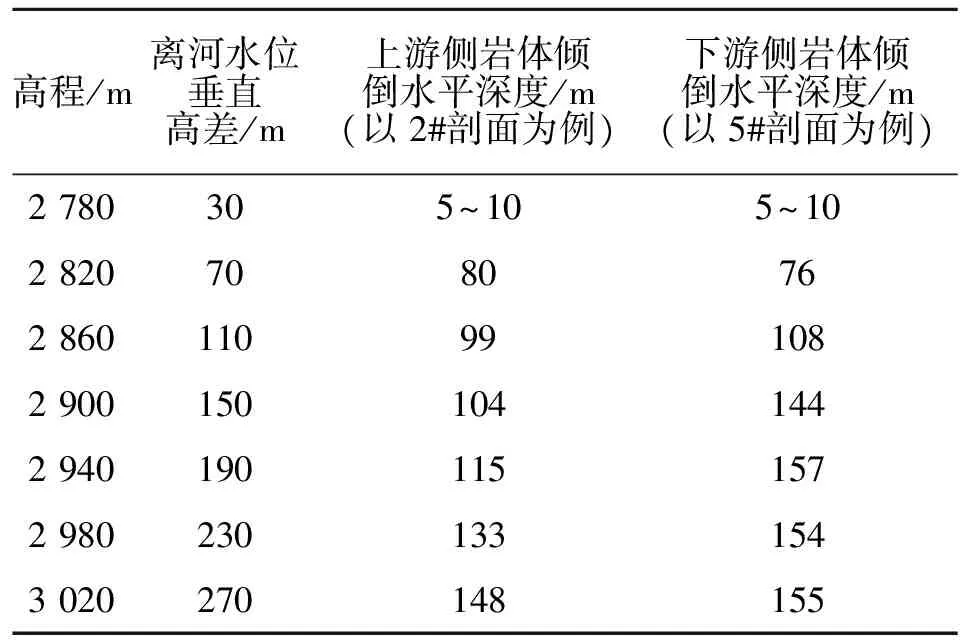
表1　4#倾倒体不同高程倾倒水平深度Tab.1　Horizontal depth of toppling of 4# toppling mass at different heights

3　有限元稳定性分析

3.1　离散化的有限元方法

传统的有限元方法在分析岩体的大变形、不连续等特性时存在局限性。离散化的有限元是在传统有限元程序FINAL[13]与ROCKS基础上开发的,将传统有限元与界面单元相结合,能够模拟岩体的变形、滑移、翻滚等失稳特性。

传统的接触面分析模型——Goodman节理单元[14]常用来模拟岩体中的断层、剪切带、结构面等不连续区域。但是由于引入了接触面的虚拟法向和切向刚度,使得该接触面单元在实际应用中受到很大限制。Katona[15]提出了一种不用刚度系数的摩擦型接触界面单元来模拟两物体间的滑动摩擦、张开和闭合过程,但这种单元采用的是常接触力的二节点简单单元,因此很难适应接触面复杂的问题。Swoboda[16]在Katona的基础上提出了一种新的界面接触单元(COJO element),见图4。此单元直接将接触面上的法向、切向接触应力作为附加未知量,克服了传统的接触单元的不足。同时能够考虑接触面的固定、滑动、张开三种接触条件,并且收敛迅速,能很好模拟具有初始裂缝和无初始裂缝两物体间的摩擦滑动、张开和闭合。

图4　接触界面单元模型Fig.4　Contact-interface element model

3.2　模型建立

本文选取4#倾倒体靠近上游侧的2#剖面为研究对象,地质剖面见图5。由图5所示,中、高高程处(2 900～2 980 m)存在多条断层及软弱结构面,大部分倾向坡内,对边坡岩体的稳定性不起控制作用,但是对边坡的变形破坏模式有较大影响。仍有少量弱面倾向坡外,这些弱面的相互组合可能会形成不稳定块体,甚至形成潜在的滑体。如平洞PD65洞内43 m处揭露的f18断层,产状NW354°∠30°,缓倾向坡外,断层破碎带宽度10～20 cm,充填岩屑、岩粉和黄色夹泥,胶结性较差。根据对边坡地质条件及探洞、钻孔等资料分析,建立相应剖面的概化模型见图6。该模型以不同高程的倾倒深度作为可能的破坏底面(潜在滑动面1),即主滑面;f18断层与后缘拉裂带组合形成潜在滑动面2。

图5　4#倾倒体典型地质剖面Fig.5　Typical geological section of 4# toppling mass

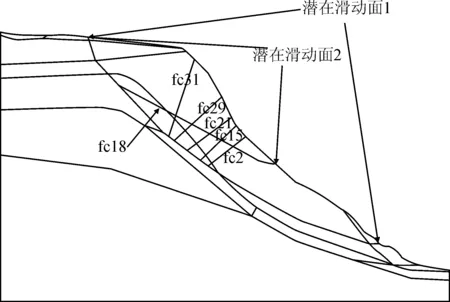
图6　2#剖面几何概化模型Fig.6　Geometric model of 2# section

图7为离散化的有限元分析模型和坡表关键点分布示意图。关键点号由坡顶到坡底分别为1～10。模型侧边界施加法向位移约束,底部边界施加位移全约束,坡面为自由边界。岩土体采用三角形六节点单元(LST),断层及结构面采用3.1节所介绍的接触界面单元。

图7　有限元网格示意图Fig.7　Diagram of finite element mesh

3.3　参数选取

根据岩体风化程度和岩性的不同,将边坡的主要岩体类型分为Ⅱ类、Ⅲ2类、Ⅳ2类,岩体类型分区见图8。岩体物理力学参数见表2,结构面参数取值见表3。水下岩体的软化系数为:强风化岩体取0.60,弱风化岩体取0.72,基岩取0.85。计算中,水下岩体容重取饱和容重,弹性模量和抗剪强度参数c、tanφ按照软化系数进行折减[17]。

图8　边坡岩体类型分区Fig.8　Rock mass partition of slope

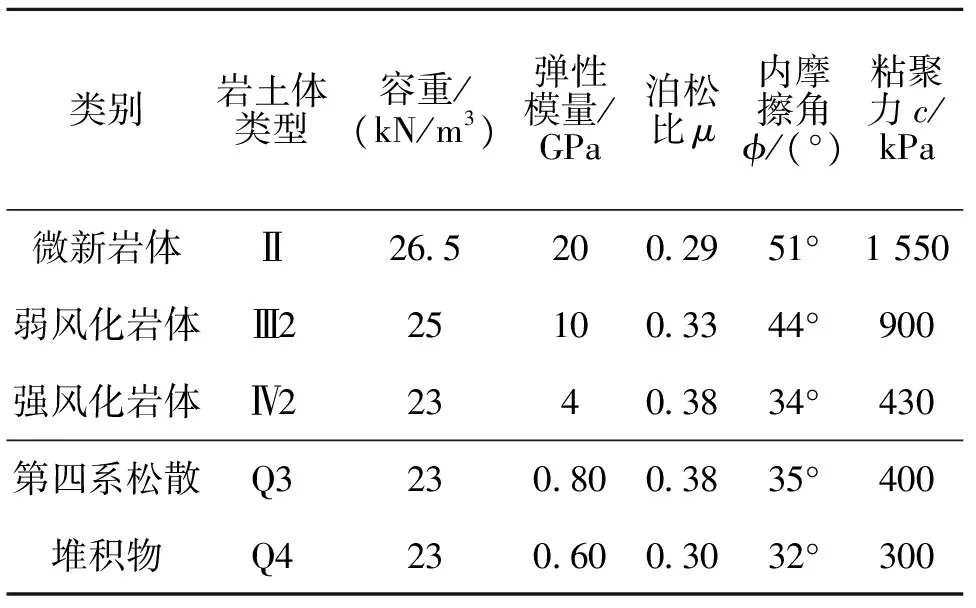
类别岩土体类型容重/(kN/m3)弹性模量/GPa泊松比μ内摩擦角ϕ/(°)粘聚力c/kPa微新岩体Ⅱ2652002951°1550弱风化岩体Ⅲ2251003344°900强风化岩体Ⅳ223403834°430第四系松散Q32308003835°400堆积物Q42306003032°300

表3　结构面计算参数Tab.3　Calculation parameters of structural plane

3.4　计算结果分析

库水位上升工况水位由初始河流水位2 759.6 m逐步上升到正常蓄水位2 990.0 m,库水位骤降工况水位由正常蓄水位2 990.0 m迅速下降到初期蓄水位2 925.0 m。通过分析边坡在强降雨、库水位上升及库水位骤降条件下的受力、变形特征,综合评价4#倾倒体的稳定性。

图9为各工况坡表关键点位移图。能够直观看出,地下水的作用导致坡体变形明显增加。尤其是库水位骤降使得整个滑体水平向位移显著增大,较骤降前平均增值高达60 mm(图9(a))。

图9　各同工况各关键点位移Fig.9　Displacement of key points in each condition

图10为库水位影响下边坡的有限元网格变形图。由图10(a),水库蓄水使得坡体内地下水位逐渐上升,岩体浸水软化范围增大,滑体底部变形较小,而上部变形相对明显。边坡后缘出现滑移现象,错动范围20 mm左右,但滑动面单元未开裂。表明蓄水虽然对边坡的稳定性产生了一定程度的影响,但并未真正“威胁”到其安全性。

企业重组业务在纳税筹划时要慎重选择重组方案，如重组形式、支付方式、所得税相关优惠条款等，本文简要介绍了重组业务纳税筹划时应注意的方面，并以企业并购这一典型的业务重组活动为例，具体介绍纳税筹划内容。

图10　库水位变化条件下有限元网格变形示意图Fig.10　FEM mesh deformation under reservoir water level change

库水位骤降对岩体变形的影响十分显著。由图10(b),边坡中、高高程处存在数条倾角不同的反倾结构面,易与其他顺层结构面组合,切割滑体形成不稳定块体。库水位骤降时,除了坡体内地下水位陡降部分岩体浮托力消失使得有效重度增加,坡体内外的水头差还导致岩体内地下水渗流运动产生一定的动水压力。结构面的不利组合形式加之地下水的力学作用,导致滑体中、上部岩体表现出明显的向临空面倾倒变形的趋势。边坡后缘出现较大的拉裂缝和错台现象;坡脚处位移明显,模拟滑动面的摩擦 ——界面单元普遍“滑动”。

图11为各工况下边坡的塑性区分布。表4为1#、2#滑面各工况所得安全系数。4#倾倒体中、高高程处岩体受反倾结构面的影响,其变形模式主要为倾倒变形,故各工况2#滑面的滑动安全系数均大于主滑面。

图11　各工况边坡塑性区分布范围Fig.11　Distribution range of plastic zone of each condition

计算工况自然工况降雨工况库水位上升库水位骤降1#滑面1191041210882#滑面153126162092

降雨入渗使得岩体结构面的剪切强度降低,岩体内部孔隙水压力增大,估安全系数较自然状态有所降低,主滑面接近临界失稳状态。暴雨工况下边坡的塑性区范围较自然状态显著增大,且集中在坡体中上部和结构面密集处(见图11(b))。

库水位上升条件下,各滑面安全系数较自然状态略有增大。其原因是:虽然蓄水导致边坡岩体浸水软化范围增大,但是浸水岩体受浮托力的影响,有效重度减小使得滑体的下滑力减小,反而有利于边坡的稳定。库水位骤降时,各滑面安全系数急剧降低到1.0以下,塑性区贯通整个滑动面(见图11(d)),边坡发生整体失稳。

综上所述,4#倾倒体受岩体结构面组合形式和地下水变化的影响,表现出上部倾倒、下部滑移的变形特征。上部岩体的倾倒变形使得下部滑体的下滑力增大,而下部滑体的滑移开裂是由坡脚向内部岩体逐渐扩展的。因此,4#倾倒体的失稳模式为牵引式倾倒破坏。

4　结　论

本文依托实际工程,结合工程地质特征与数值仿真分析,得出以下结论:

1) 离散化的有限元方法将传统有限元与界面单元相结合,克服了传统有限元方法的局限性,能够较好的模拟边坡岩体的变形、滑移、倾倒等失稳特性。

2) 库水位上升对边坡稳定性的影响不能一概而论,应针对具体工程进行分析,主要表现为岩体受到的浮托力和结构面参数的弱化。库水位骤降使得岩体内部产生较大的动水压力,对边坡的稳定非常不利。对于库岸边坡,应着重分析水位骤降时的稳定性。

3) 茨哈峡水电站4#倾倒体为典型的反倾层状岩质边坡,自然状态下的稳定性较好。但是受结构面不利组合形式和地下水作用的影响,边坡在降雨和库水骤降条件下可能会发生变形失稳。其变形模式为上部倾倒、下部滑移的组合形式,失稳模式为牵引式倾倒破坏,底滑面为边坡稳定的控制性结构面。

4) 针对于此类边坡,应加强坡面防渗和坡体排水,降低岩体的孔隙水压力。施工期应控制开挖坡度,对坡体前缘采取必要的加固措施,控制坡脚处的变形。

参考文献:

[1] 崔政权, 李宁. 边坡工程——理论与实践最新发展 [M]. 北京: 中国水利水电出版社, 1999.

[2] 黄润秋. 20世纪以来中国的大型滑坡及其发生机制 [J]. 岩石力学与工程学报, 2007, 26(3): 433-454.

HUANG Runqiu. Large-scale landslides and their sliding mechanisms in China since the 20th century [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(3): 433-454.

[3] 何满潮, 姚爱军, 鹿粗, 等. 边坡岩体水力学作用的研究 [J]. 岩石力学与工程学报, 1998, 17(6): 662 -666.

HE Manchao, YAO Aijun, LU Cu, et al. Study of mechanical functions of underground water in slope rockmass [J]. Chinese Journal of Rock Mechanics and Engineering, 1998, 17(6): 662-666.

[4] 刘才华, 陈从新, 冯夏庭, 等. 地下水对库岸边坡稳定性的影响 [J]. 岩土力学, 2005, 26(3): 419-422.

LIU Caihua, CHEN Congxin, FENG Xiating, et al. Effect of groundwater on stability of slopes at reservoir bank [J]. Rock and Soil Mechanics, 2005, 26(3): 419-422.

[5] 郭志华, 周创兵, 盛谦, 等. 库水位变化对边坡稳定性的影响 [J]. 岩土力学, 2005，(增刊2): 29-32.

GUO Zhihua, ZHOU Chuangbing, SHENG Qian, et al. Influence of reservoir water level variation on slope stability [J]. Rock and Soil Mechanics, 2005，(S2): 29-32.

[6] 廖红建, 盛谦, 高石夯, 等. 库水位下降对滑坡体稳定性的影响 [J]. 岩石力学与工程学报, 2005, 24(19): 3454-3458.

LIAO Hongjian, SHENG Qian, GAO Shihang, et al. Influence of drawdown of reservoir water level on landslide stability [J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(19): 3454-3458.

[7] 梁学战, 陈洪凯. 库水位升降条件下不同渗透性的滑坡体稳定性变化规律 [J]. 中国地质灾害与防治学报, 2012,23(4): 20-26.

LIANG Xuezhan, CHEN Hongkai. Stability variation of landslide with different permeability coefficient following reservoir water level fluctuation [J]. The Chinese Journal of Geological Hazard and Control, 2012,23(4): 20-26.

[8] 朱冬林, 任光明, 聂德新, 等. 库水位变化下对水库滑坡稳定性影响的预测 [J]. 水文地质工程地质, 2002, 29(3): 6-9.

ZHU Donglin, REN Guangming, NIE Dexin, et al. Effecting and forecasting of landslide stability with the change of reservoir water level [J]. Hydrogeology and Engineering Geology, 2002, 29(3): 6-9.

[9] 董金玉, 杨继红, 孙文怀, 等. 库水位升降作用下大型堆积体边坡变形破坏预测 [J]. 岩土力学, 2011, 32(6): 1774-1780.

DONG Jinyu, YANG Jihong, SUN Wenhuai, et al. Prediction of deformation and failure of a large-scale deposit slope during reservoir water level fluctuation [J]. Rock and Soil Mechanics, 2011, 32(6): 1774 -1780.

[10] 刘晓丽, 林鹏, 韩国锋, 等. 裂隙岩质边坡渗流与非连续变形耦合过程分析 [J]. 岩石力学与工程学报, 2013, 32(6): 1248-1256.

LIU Xiaoli, LIN Peng, HAN Guofeng, et al. Hydro-mechanical coupling process on rock slope stability based on discontinuous deformation analysis and discrete fracture network models [J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(6): 1248-1256.

[11] 李邵军, KNAPPETT J A, 冯夏庭. 库水位升降条件下边坡失稳离心模型试验研究 [J]. 岩石力学与工程学报, 2008, 27(8): 1586-1593.

LI Shaojun, KNAPPETT J A, FENG Xiating. Centrifugal test on slope instability influenced by rise and fall of reservoir water level [J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(8): 1586-1593.

[12] 李卓, 何勇军, 盛金保, 等. 降雨与库水位共同作用下近坝库岸边坡滑坡模型试验研究 [J]. 岩土工程学报, 2017, 39(3): 452-459.

LI Zhuo, HE Yongjun, SHENG Jinbao, et al. Landslide model for slope of reservoir bank under combined effects of rainfall and reservoir water level [J]. Chinese Journal of Geotechnical Engineering, 2017, 39(3): 452-459.

[13] 李宁, 陈波, 陈飞雄, 等. 奥地利岩土工程软件FINAL的应用与开发 [J]. 西安公路交通大学学报, 2000, 20(1): 27-33.

LI Ning, CHEN Bo, CHEN Feixiong, et al. Development and application of the Austrian software FINAL in China [J]. Journal of Xi’an Highway University, 2000, 20(1): 27-33.

[14] GOODMAN R E, TAYLER R L, BREKKE T L. A model for the mechanics of jointed rock [J]. Journal of the Soil Mechanics and Foundations Division, 1968, 94(3): 637-660.

[15] KATONA M G. A simple contact-friction interface element with applications to buried culverts [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1983, 7(3): 371-384.

[16] SWOBODA G, MARENCE M. Numerical modelling of rock bolts in intersection with fault system [C]∥Proc. Numerical Models in Geomechanics, 1992: 729-738.

[17] 张有天. 岩石水力学与工程 [M]. 北京: 中国水利水电出版社, 2005.