基于伪故障度生成枚举树的极小诊断求解方法
欧阳丹彤 智华云 刘伯文 张立明 张永刚
(吉林大学计算机科学与技术学院 长春 130012) (符号计算与知识工程教育部重点实验室(吉林大学) 长春 130012) (ouyangdantong@163.com)
基于模型诊断(model-based diagnosis, MBD)问题对人工智能领域的发展具有十分重要的推动作用[1].其主要思想是根据设备的内部结构和行为来诊断该设备,从模型和观测出发推理出设备的故障组件,解释预期行为和观测行为之间的差异.基于模型诊断过程主要分为3个步骤:1)诊断产生.已知一个差异,决定可能失灵的组件导致该差异.2)诊断测试.测试诊断过程中产生的所有诊断解,找出能够解释设备所有观测的组件集合.3)诊断辨别.若有多个诊断通过测试,搜集额外信息以得到最后的诊断解.
著名MBD专家Reiter[2]提出了根据极小冲突集求解极小碰集(即系统的极小诊断解)的方法HS-Tree,但该方法要遍历整棵枚举树,导致诊断空间很大且会因剪枝丢失诊断解.针对这些缺点,Greiner等人[3]提出了改进方法HS-DAG,解决了HS-Tree的丢解问题.随着对MBD问题深入的探索和研究,许多新的方法被提出.Stein等人[4]提出的诊断方法允许待诊断系统的组件及其行为有缺省信息,并用合理的假设表示系统的异常行为,有效地提升了该方法对特定问题的求解效率.赵相福等人[5]提出了CSISE-Tree方法,在对集合枚举树进行剪枝优化的基础上求出诊断系统所有的诊断解.欧阳丹彤等人[6]提出了利用标志传播求解系统所有候选解的方法,通过传播系统的输出标志来判断组件集合是否是诊断解.Schmitz等人[7]利用部分诊断解优化冲突集,并提出了根据极小冲突集求诊断解的时序诊断方法.
近年来,命题可满足问题(propositional satis-fiability problem, SAT)受到国内外学者的广泛关注[8].Cook[9]于1971年首次证明SAT问题是NP完全问题,人工智能领域的很多NP问题都可以转化成SAT问题求解[10]且研究表明,与直接求解NP问题相比,将其转化成SAT问题后求解更加高效.一些优秀的求解引擎已被广泛应用于布局布线、自动测试矢量、电路等价性验证、智能规划等[11]领域.随着对MBD问题研究的深入,发现该问题也可以转换成SAT问题求解且已取得显著成果.
基于SAT求解器的发展,国内外许多学者开始投入到结合SAT求解诊断的研究领域中.Feldman等人[12]提出利用带权重的MaxSat求解MBD,该方法将子句分为hard子句和soft子句,并对子句赋予权重,最终要求满足子句权重乘积之和最大,进而得到所有诊断解.Metodi等人[13]提出了一种新的编码方式,将MBD编码成布尔可满足问题来求解,并对诊断系统进行了复杂的预处理.Marques-Silva等人[14]提出将MBD转成MaxSat问题求解的方法,根据阻塞结点和边、过滤结点和边缩减诊断系统规模,减小诊断系统求解空间.国内学者周建华等人[15]利用SAT求解器结合LLBRS-Tree算法求出诊断系统所有的极小诊断解,此方法是目前基于枚举树结构利用SAT求解诊断效率较高的方法.
LLBRS-Tree方法从叶结点开始向上遍历枚举树直到根结点为止,同时基于非诊断解的祖先结点一定不是诊断解进行无解剪枝[15]以及诊断解的子孙结点一定不是极小诊断解进行有解剪枝[15],通过有解剪枝和无解剪枝剪掉大量结点.本文在LLBRS-Tree方法的基础上进行了改进,提出了根据组件的静态伪故障度和动态伪故障度生成枚举树,动态更新枚举树遍历顺序进行剪枝的方法DYN-Tree.该方法计算每个组件发生故障的概率(记为静态伪故障度),根据组件的静态伪故障度生成枚举树,当调用SAT求解器求得一个组件集合是极小诊断解时,更新该集合中组件的动态伪故障度,重新动态生成新的枚举树遍历顺序,对新生成的枚举树进行有解剪枝和无解剪枝,直到求得诊断系统的所有极小诊断解为止.该方法能够较早地发现极小诊断解,裁剪掉大量冗余的诊断解.
1 预备知识
本节首先介绍一些基于模型诊断的相关概念,然后介绍如何将基于模型诊断问题转化成SAT问题求解.
1.1 基于模型诊断的相关概念
定义1. 诊断系统[1]. 一个系统定义为一个三元组(SD,COMPS,OBS),其中:SD是系统描述,是谓词公式的集合;COMPS是系统的组成部件集合,是一个有限常量集合;而OBS是观测集合,是谓词公式的有限集合.
AB意味着“abnormal”(反常),当部件c∈COMPS反常时,AB(c)为真,否则,AB(c)为真.
定义2. 基于一致性诊断[1]. 设组件集合Δ⊆COMPS,称Δ为关于(SD,COMPS,OBS)的一个基于一致性诊断,若SD∪OBS∪{AB(c)|c∈COMPS-Δ}是可满足的.
定义3. 极小诊断解[1]. 称关于(SD,COMPS,OBS)的一个基于一致性诊断Δ是极小的诊断,当且仅当不存在Δ的任何真子集也是关于(SD,COMPS,OBS)的一个基于一致性诊断.
在弱故障模型诊断中,根据极小诊断解的定义可知:若集合A是(SD,COMPS,OBS)的一个极小诊断解,其中有B⊆COMPS,C⊆COMPS,则:
1) 若A⊂C,则C一定是该系统的一个基于一致性诊断,但C不是极小诊断解;
2) 若B不是诊断解且C⊂B,则C一定不是该系统的基于一致性诊断.
根据1)和2)可知,如果某组件集合不是基于一致性诊断,那它的真子集肯定不是基于一致性诊断;基于一致性诊断解的真超集依然是该系统的诊断解,但不是极小诊断解.本文利用上述性质对集合枚举树进行剪枝,提高诊断解求解效率.
1.2 将基于模型诊断转化成命题可满足问题
本节介绍SAT问题的基本定义,并介绍如何将基于模型诊断问题转化为SAT问题求解的方法.
SAT问题是指对于给定的一个CNF合取范式Q=C1∧C2∧…∧Cn,X={x1,x2,…,xm}是该公式的变量集合,Ci(i=1,2,…,n)是变量x1,x2,…,xm或变量否定的析取式,如果变量x1,x2,…,xm找到一组赋值能够使得公式Q最后取值为真,则称Q是可满足的,否则是不可满足的.
SAT求解器的输入是CNF形式的文件,故需要将电路系统的内部结构信息、观测信息和组件信息3部分用CNF子句表示,并构成一个CNF文件.SAT求解器处理该CNF文件,如果最后返回结果为真,那么该CNF文件是可满足的,否则不是.
首先,我们先将诊断系统转换成CNF描述形式,图1是诊断系统中常用的组件.

Fig. 1 The components of system图1 系统组件
在电路系统中,输入有高电平、低电平之分,本文中,输入为正数代表高电平,负数代表低电平.比如图1(a)中或门,输入端口“5”表示的是高电平,而不是电平值.假设图1组件均正常,根据离散数学和数字逻辑知识,再结合这些组件的输入,可以推出组件对应的输出,则图1中各组件的CNF子句形式表示如下:
假设上述组件均正常,根据离散数学和数字逻辑知识,再结合这些组件的输入,可以推出组件对应的输出,并以CNF子句的形式表示如下.
1) OR(或门)
(5∨6∨-13∨N1)∧(-5∨13∨N1)∧(-6∨13∨N1);
2) AND(与门)
(-7∨-8∨14∨N2)∧(7∨-14∨N2)∧(8∨-14∨N2);
3) XOR(异或门)
(9∨10∨-15∨N3)∧(-9∨-10∨-15∨N3)∧(-9∨10∨15∨N3)∧(9∨-10∨15∨N3);
4) NOR(或非门)
(11∨12∨16∨N4)∧(-11∨-16∨N4)∧(-12∨-16∨N4).
本节描述了怎样将系统组件转换成CNF表达式,下面将给出图1(a)中或门的CNF子句在文件中的组织形式:

pcnf331-51310∕*p,cnf是文件语法,第1行第1个3表示变量个数,第2个3表示子句个数,1是组件个数*∕56-130∕*5,6代表文字,-13是变量的否定,每行都是一个子句,子句都以0结束*∕-61310∕*最后1个子句可表示为(-6∨13∨1)*∕
通过上面的转换,可以将系统的内部功能信息、系统观测以及组件信息表示成CNF命题形式,然后调用SAT求解器处理,根据SAT求解器返回值求解该系统的基于一致性诊断解.第2节将介绍求解系统对应的所有诊断解的具体算法.
2 SE-Tree及LLBRS-Tree诊断求解方法
第1节介绍了如何将基于模型诊断问题转化成SAT问题求解,本节将要介绍求解诊断基于树结构的2种方法:基于集合枚举树(set-enumeration tree, SE-Tree)的遍历方法和反向遍历的LLBRS-Tree方法.
2.1 根据集合枚举树求解所有诊断
集合枚举树(SE-Tree)由国外学者Rymon[16]提出:它可以枚举出一个集合所有的子集.集合SS有M个元素,SE-Tree可以按照某种顺序枚举出SS的2M个子集;设SS={N1,N2,N3,N4},默认枚举树从第0层开始,如果枚举树第1层从左到右组件出现的顺序分别是{N4},{N3},{N2},{N1},则集合SS的完全枚举树如图2所示:

Fig. 2 SE-Tree of the set {N1,N2,N3,N4}图2 集合{N1,N2,N3,N4}的完全枚举树
SE-Tree在求系统的诊断解时是完备的算法,它遍历集合枚举树中所有结点,每当求解得到新的诊断解时,就会更新原来的诊断解,以保证最后剩余的都是极小诊断解.虽然SE-Tree是完备的,但没有任何剪枝优化策略,效率并不高.赵相福等学者在SE-Tree的基础上提出了CSISE-Tree方法.该算法通过广度优先策略遍历翻转的集合枚举树,对非诊断解及其所有的真子集进行剪枝.
2.2 LLBRS-Tree算法求诊断解
周建华等人[15]在CSISE-Tree的基础上提出了改进算法LLBRS-Tree,下面介绍该算法的相关定义及实现.
定义4. 反向搜索[15].对于一个集合枚举树,称从树的叶结点向根结点遍历的过程为反向搜索.
定义5. 有解剪枝[15].对于一个集合枚举树,如果在遍历它时发现某个结点是诊断解,那么该结点的所有子孙结点一定不是极小诊断解,因此,可以直接跳过这些子孙结点,不再判断.称跳过该结点的子孙结点的过程为有解剪枝.
定义6. 无解剪枝[15].在遍历一个枚举树时,发现某个结点不是系统的诊断解,那么该结点的父结点及其祖先结点也不是诊断解,因此,可以直接跳过这个结点的父结点和其祖先结点,不再判断.称跳过该结点的父结点及其祖先结点的过程为无解剪枝.
算法LLBRS-Tree对集合枚举树反向搜索,在从叶结点向根结点遍历搜索过程中,同时进行有解剪枝和无解剪枝,减掉枚举树中的部分结点.LLBRS-Tree算法的伪代码如下:
算法1. LLBRS-Tree算法.
输入: 系统描述CNF的文件SysDis.CNF、系统观测的CNF文件SysObs.CNF、极小诊断解的最大诊断长度MinDigLen;
输出: 极小诊断解的集合DigRes[].
局部变量: 待判断的第1层某个结点及其子树sub-tree.
① 初始化DigRes=∅;
② 从SysDis.CNF文件中的第1行中读取出诊断系统变量个数、CNF子句个数及组件个数;
③ 将集合枚举树的第1层最左边的结点及其子树赋值给sub-tree,子树的高度是MinDigLen(默认集合枚举树从第0层开始);
④ while(集合枚举树中存在第1层结点及其子树还没判断)
while(sub-tree判断未完成)
先判断sub-tree最后1层最左边的结点是否是诊断解;
if (该结点是诊断解)
将结点加入到集合DigRes中,并且删除在DigRes集合中该结点的所有真超集;
删除枚举树中该结点的所有子孙结点;
对该结点的父结点进行判断;
else
删除该结点的父结点及其祖先结点;
访问下一个没有被访问及其删除的叶结点;
endif
将第1层的下一个结点及其子树赋值给sub-tree,接着对sub-tree进行判断;
endwhile
endwhile
⑤ 返回集合DigRes.
在弱故障模型诊断中,LLBRS-Tree的提出对于系统的极小诊断解的求解效率有了一定的提升,主要优点有2项:
1) 根据诊断解的定义,非诊断解的所有真子集均不是诊断系统的诊断解.LLBRS-Tree利用该特征进行剪枝,避免了一些非诊断解的判断.
2) 根据极小诊断解的定义,极小诊断解的所有真超集均不是极小诊断解.因此,在遍历枚举树时我们可以不去判断极小诊断解的真超集.
与CSISE-Tree相比,LLBRS-Tree在求解极小诊断解的效率时有很大的提升,但是在求解过程中,该算法遍历了大量极小诊断解的真超集,而这些真超集不是最终解,最后都会被删除.针对这种情况对该算法进行了改进,能减少很多冗余解(极小诊断解的真超集)的产生,剪掉大量极小诊断解的真超集,提高问题求解效率.
3 基于伪故障度动态生成枚举树的诊断方法
通过分析可知,在一个电路系统中,极小诊断解的数量并不多,剩下的大多数结点是非诊断解和冗余解.基于此,提出针对冗余解的剪枝策略.该算法是完备算法,不需要访问枚举树中所有结点,只遍历部分结点可以得到系统所有的极小诊断解.
定义7. 故障输出.对于一个电路系统,如果该终端组件的实际输出和观测输出不一样,称该终端组件的输出为故障输出.
通过分析电路内部结构关系、系统观测行为和预期行为,得知每个组件出现故障的概率并不相同,与故障输出相关的组件比一般的组件出现故障的概率要大.
定义8. 部分诊断解.设在诊断系统中与某组件comp输入相连组件个数是N,如果其中M(1≤M≤N)个组件同时故障与组件comp故障时的故障输出相同,即M个组件同时故障能解释组件comp故障时的故障输出,则此M个组件集合称为部分诊断解.
定义9. 静态伪故障度.称系统中某组件comp发生故障的概率为该组件的静态伪故障度(记为SD),并且故障输出对应组件的SD=1,正常组件的SD=0;设组件comp的SD=Dc(Dc>0),与组件comp对应的部分诊断解中有M个组件,这M个组件的SD分别为DcM;若某组件的SD有多个取值Di(i=1,2,…,m),则该组件的SD=max{Di|i=1,2,…,m}.
由定义9计算出每个组件的SD,再根据组件的SD大小对组件进行排序.在生成枚举树时,SD值大的组件排在前面,遍历时首先访问这些组件组成的集合.比如在图2中,我们认为组件4的静态伪故障度最大(组件i的伪故障度记为SDi),组件1的静态伪故障度最小,即SD4>SD3>SD2>SD1.并且集合枚举树随着极小诊断解的产生而动态改变.
定义10. 动态伪故障度.诊断系统中,记某组件comp在枚举树第1层中位置是否变化的标志为该组件的动态伪故障度(简称DD).若组件comp静态伪故障度大于0,设该组件的动态伪故障度等于1,其在枚举树第1层结点中的位置不再改变.对于静态伪故障度等于0的组件,其DD初始化为0,并且根据以下2个规则更新这些组件的DD:
1) 枚举树第1层中某个集合K,以K为根结点的子树中已经有结点被访问过,更新集合K中组件的DD=1;
2) 在遍历枚举树时,搜索到一个结点为极小诊断解,且该结点中有组件的DD值为0,则这些组件的DD重新赋值为1.
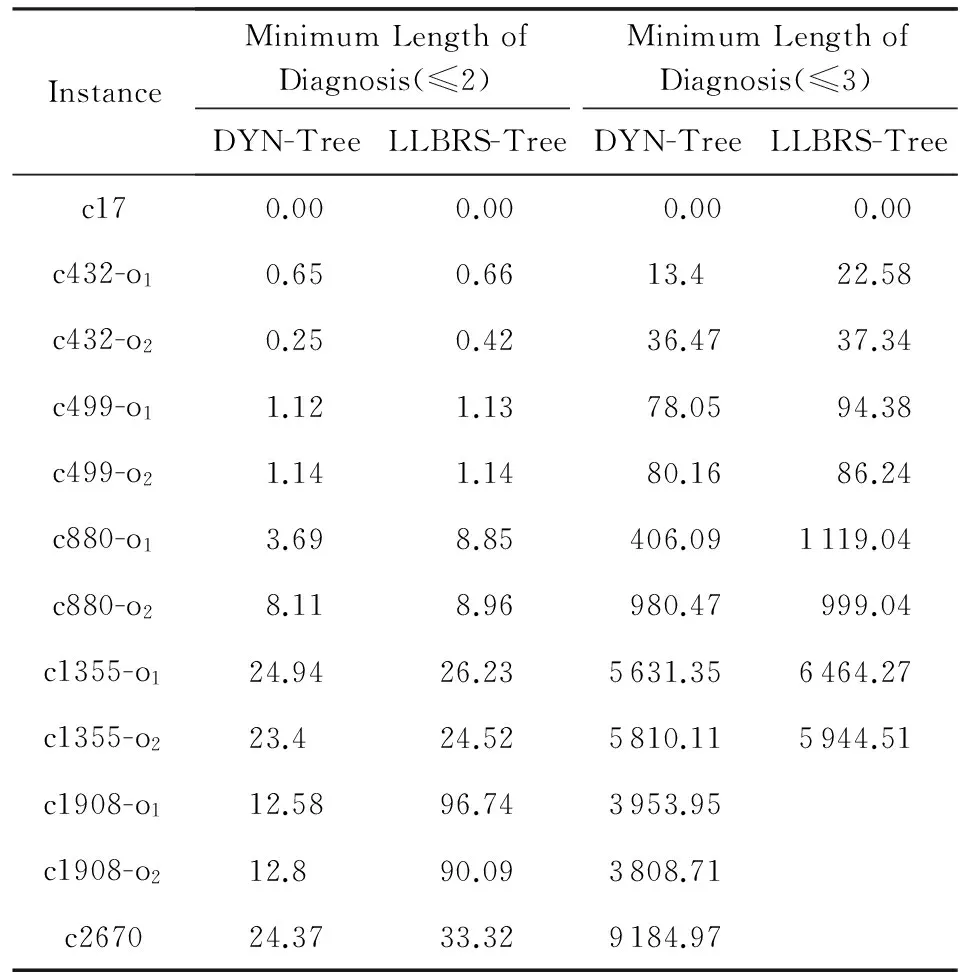
在定义10中,以方式1)改变集合K中组件的DD后,K在枚举树第1层结点中的位置不再改变;而以方式2)改变某些组件的DD值后,还要改变这些组件在枚举树第1层结点中的顺序.设枚举树第1层结点从左到右对应的组件分别是:comp1,comp2,…,compj,compj+1,…,compk,compk+1,…,compn(j 定义11. 最左结点[17].以某结点为根结点形成的子树中,我们称最底层最左边的结点为最左结点. 如图2中的{N4,N3,N2,N1}是最左结点. 定义12. 兄弟结点[17].如果若干个结点有共同的父结点,则称这些结点是兄弟结点. 如图2中的{N4,N3},{N4,N2},{N4,N1}是兄弟结点. 下面我们给出该算法的伪代码. 算法2. DYN-Tree算法. 输入: 系统描述的CNF文件SysDis.CNF、系统观测的CNF文件SysObs.CNF; 输出: 诊断系统的极小诊断解集合Res. ①initialize(); ②calweight(SysDis.CNF,SysObs.CNF); ③ while(S≠∅) ④flag=issolve(S); ⑤ if (flag==1) ⑥addsol(S,Res); ⑦updatetree(true,S); ⑧ if (S是以S的父结点为根结点的子树中最左边分支上的结点) ⑨S←S的父结点; ⑩ else if (S是从最底层向上回溯后的结点) S←下一个叶结点; 在算法2中,步骤②calweight算法计算系统的故障输出,找到能够解释故障输出的组件集合,进而计算出每个组件的SD,生成新的集合枚举树,下面就是遍历集合枚举树的步骤.步骤③~,当枚举树没有被遍历完时进入循环体,继续寻找可能的诊断解.步骤④,issolve(S)判断集合S是否是诊断解.步骤⑤⑥,当S是诊断解时,addsol(S,Res)更新诊断解的集合Res,如果Res中有S的真超集,那么用S替换S的真超集;步骤⑦,若S是极小诊断解,算法updatetree更新S中动态伪故障度等于0的组件,随后对组件重新排序,动态生成新的枚举树;步骤⑧~表示S是诊断解时,确定下一个要遍历的结点;步骤,以枚举树第1层的结点为根结点的子树中有结点被遍历过,算法updatetree更新该根结点组件的动态伪故障度;步骤,结点S不是诊断解时确定下一个要访问的结点;最后返回极小诊断解的集合. 计算系统组件静态伪故障度的算法calweight如下. 算法3.calweight()算法. 输入:系统描述的CNF文件 SysDis.CNF、系统观测的CNF文件SysObs.CNF; 输出: 系统的部分诊断解PartSol. 局部变量: 故障输出的组件和可能故障的组件ErrorOut,可能故障组件的输入In_Out,与故障输出组件和可能故障的组件相关的组件CComp. ①ErrorOut←由SysDis.CNF和SysObs.CNF找到系统故障输出组件; ② for(i=0;i ③In_Out←ErrorOut[i]的输入; ④ for(j=0;j ⑤CComp←找到以In_Out[j]作为输出的组件; ⑥ if(对CComp中某些组件的输出取反后能解释故障输出) ⑦PartSol←输出值被取反的组件组成的集合; ⑧ErrorOut←输出值被取反的组件; ⑨ endif ⑩ endfor 算法3的步骤①找到系统故障输出的组件;步骤②~⑤求解哪些组件的输出是故障输出组件及可能故障组件的输入;步骤⑥~⑧,CComp中的若干个组件均故障能够解释故障输出,那么这些组件组成的集合是部分诊断解,并且该部分诊断解中组件故障的概率较大.最后返回部分诊断解的集合. 计算组件动态伪故障度的算法updatetree如下. 算法4.updatetree()算法. 输入:判断结点S是否极小诊断解的boolean变量,枚举树中一个结点S. ① if(boolean==true) ② for(i=0;i ③S[i].DD=1; endfor ④ else ⑤S[0].DD=1; ⑥ endif 算法4的步骤②③,boolean=true时,说明结点S是极小诊断解,S中组件故障的概率比较大,故S中如果有组件DD=0,更新这些组件的DD=1;步骤⑤,以枚举树第1层结点K为根结点的子树中有结点被遍历过,那么结点K在枚举树中的位置不再改变,赋值结点K中组件的DD=1. Fig. 3 The circuit diagram of component set {N1,N2,N3,N4,N5,N6,N7}图3 组件{N1,N2,N3,N4,N5,N6,N7}的电路图 实现了周建华等人[15]提出的LLBRS-Tree方法和本文提出的DYN-Tree方法,并对2个方法的效率进行了对比.实验平台如下:Dell GX620,Ubuntu 12.04,GCC编译器,CPU AMD AthlonTM64 X2 Dual Core Processor 3600+1.9 GHz,3.00 GB RAM.LLBRS-Tree方法和DYN-Tree方法调用的SAT求解器均是Picosat[18]. 本次使用的测试例子主要来自ISCAS-85的基准电路,包括c17,c432,c499,c880,c1355,c1908,c2670.对于一个故障电路,系统观测不同,最后的极小诊断解一般不同,我们改变某些电路的系统观测以得到更多的测试例子,使得DYN-Tree算法更具有说服力.如果一个电路有多个不同观测,我们分别命名为:电路名-o1,电路名-o2,…,电路名-on,比如,c432有2个不同的观测,我们可以分别命名成c432-o1,c432-o2. 本文分别对LLBRS-Tree方法和DYN-Tree方法在上述电路测试用例上进行测试,极小诊断长度是1时,所有组件都需要判断,理论上2个算法效率一样.因此,表1只需列出极小诊断长度为2,3时2个算法的时间.理论上,极小诊断解长度越长,DYN-Tree算法剪掉的结点越多,效率提高的越多,这是由于在LLBRS-Tree算法的枚举树中,遍历位置靠后的大量冗余解在DYN-Tree算法生成的动态枚举树中都被优先提前生成,且不需要被遍历就可以剪掉.实验结果也表明极小诊断解长度是2时,DYN-Tree算法效率平均提高了8%,极小诊断是3时,DYN-Tree算法效率平均提高了15%.在表1和表2中,空白表示在10 000 s内算法求不出诊断解,极小诊断长度是3时,对于电路c1908和c2670,LLBRS-Tree均求不出诊断解,DYN-Tree可以成功地求出诊断解. 单诊断所有结点都需要判断,不存在剪枝情况.因此,表2中只列出了极小诊断长度为2,3的情况,2个算法剪掉的结点数的差值是Δ为DYN-Tree算法剪掉的结点数目减去LLBRS-Tree算法剪掉的结点数目.Picosat求解器在判断结点是否是诊断解时用了规则单元传播和分裂规则,在求解时只要有一个终端组件的实际输出和观测输出不一样就可以断定该结点是非诊断解,而确定一个结点是诊断解需要计算出所有终端组件的实际输出和观测输出都一样才行.因此,判断一个结点是诊断解比判断一个结点是非诊断解花费时间更长,而本文提出的改进算法DYN-Tree剪掉了大量的冗余解,对问题求解效率提升明显. Table 1 Solution Time表1 求解时间 s Table 2 Number of Cut Nodes表2 剪掉结点的个数 一直以来,基于模型诊断问题都是人工智能领域最重要的问题之一,本文将基于模型诊断问题转换成SAT问题并利用SAT求解器求解,简化了问题求解难度.LLBRS-Tree是目前利用SAT求解诊断效率较高的方法,此方法虽然使用了有解剪枝和无解剪枝,但是仍然有许多冗余解存在,并且通过分析得知Picosat求解器求解冗余解时耗时更长.本文提出的DYN-Tree方法根据组件的静态伪故障度生成枚举树,每当遍历到新的极小诊断解时,更新该诊断解中组件的动态伪故障度,并根据组件的动态伪故障度生成新的枚举树.该算法能够及早地发现系统的极小诊断解,剪掉大量冗余解,减少SAT求解器调用次数.实验结果表明DYN-Tree方法对于求解极小诊断解效率较LLBRS-Tree方法而言有较大提高. [1]Console L, Dressler O. Model-based diagnosis in the real world: Learned and challenges remaining[C]Proc of the 16th Int Joint Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 1999: 1393-1400 [2]Reiter R. A theory of diagnosis from first principles[J]. Artificial Intelligence, 1987, 32(1): 57-95 [3]Greiner R, Smith B A, Wilkerson R W. A correction to the algorithm in Reiter’s theory of diagnosis[J]. Artificial Intelligence, 1989, 41(1): 79-88 [4]Stein B, Niggemann O, Lettmann T. Speeding up model-based diagnosis by a heuristic approach to solving SAT[C]Proc of the 24th Int Association of Science and Technology for Development on Artificial Intelligence and Applications. Anaheim, CA: ACTA, 2006: 273-278 [5]Zhao Xiangfu, Ouyang Dantong. Deriving all minimal conflict sets using satisfiability algorithms[J]. Acta Electronica Sinica, 2009, 37(4): 804-810 (in Chinese)(赵相福, 欧阳丹彤. 使用SAT求解器产生所有极小冲突部件集[J]. 电子学报, 2009, 37(4): 804-810) [6]Ouyang Dantong, Zhang Liming, Zhao Jian, et al. Solving model-based fault diagnosis with flag propagation[J]. Chinese Journal of Scientific Instrument, 2011, 32(12): 2857-2862 (in Chinese)(欧阳丹彤, 张立明, 赵剑, 等. 利用标志传播求解基于模型的故障诊断[J]. 仪器仪表学报, 2011, 32(12): 2857-2862) [7]Shchekotykhin K, Schmitz T, Jannach D. Efficient sequential model-based fault-localization with partial diagnoses[C]Proc of the 25th Int Joint Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2016: 1164-1170 [8]Luo Chuan, Cai Shaowei, Wu Wei, et al. Double configuration checking in stochastic local search for satisfiability[C]Proc of the 28th AAAI Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2014: 2703-2709 [9]Cook S A. The complexity of theorem-proving procedures[C]Proc of the 3rd Annual ACM Symp on Theory of Computing. New York: ACM, 1971: 151-158 [10]Cai Shaowei, Su Kaile. Comprehensive score: Towards efficient local search for SAT with long clauses[C]Proc of the 23rd Int Joint Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2013: 489-495 [11]Cai Dunbo, Yin Minghao. On the utility of landmarks in SAT based planning[J]. Knowledge-Based Systems, 2012, 36(6): 146-154 [12]Feldman A, Provan G, de Kleer J, et al. Solving model-based diagnosis problems with Max-Sat Solvers and vice versa[C]Proc of the 21st Int Workshop on Principles of Diagnosis. New York: IJPHM, 2010: 185-192 [13]Metodi A, Stern R, Kalech M, et al. Compiling model-based diagnosis to Boolean satisfaction[C]Proc of the 26th AAAI Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2012: 793-799 [14]Marques-Silva J, Janota M, Ignatiev A, et al. Efficient model based diagnosis with maximum satisfiability[C]Proc of the 24th Int Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2015: 1966-1972 [15]Zhou Jianhua, Ouyang Dantong, Liu Bowen, et al. A new algorithm combining with the characteristic of the problem for model-based diagnosis[J]. Journal of Computer Rearch and Development, 2017, 54(3): 502-513 (in Chinese)(周建华, 欧阳丹彤, 刘伯文, 等. 基于模型诊断中结合问题特征的新方法[J]. 计算机研究与发展, 2017, 54(3): 502-513) [16]Rymon R. Search through systematic set enumeration[C]Proc of the 3rd Int Conf on Principles of Knowledge Representation and Reasoning. San Franasco, CA: Morgan Kaufmann, 1992: 539-550 [17]Ouyang Dantong, Liu Bowen, Zhou Jianhua, et al. A method of computing minimal conflict sets combining the structure property with the anti-depth SE-TREE[J]. Acta Electronica Sinica, 2016, 45(5): 1175-1181 (in Chinese) (欧阳丹彤, 刘伯文, 周建华, 等. 结合问题特征利用 SE-Tree 反向深度求解冲突集方法[J]. 电子学报, 2016, 45(5): 1175-1181) [18]Le Berre D, Parrain A. The SAT4j library, release 2.2[J]. Journal on Satisfiability Boolean Modeling and Computation, 2010, 7(11): 59-64 OuyangDantong, born in 1968. Professor and PhD supervisor of Jilin University. Senior member of CCF. Her main research interests include model-based diagnosis, model checking and automated reasoning. ZhiHuayun, born in 1992. Master candidate at Jilin University. Her main research interests include model-based diagnosis, SAT problem and automated reasoning (13756941032@163.com). LiuBowen, born in 1993. Master candidate at Jilin University. His main research interests include model-based diagnosis, SAT problem and automated reasoning (1591365445@qq.com). ZhangLiming, born in 1980. PhD, post-doctor in Jilin University. His main research interests include model-based diagnosis, model checking and Boolean satisfiability. ZhangYonggang, born in 1975. PhD. Associate professor in Jilin University. His main research interests include constraint satisfaction problem and automated reasoning.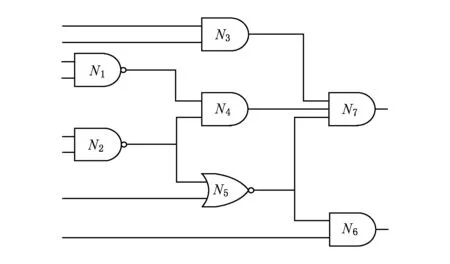

4 实验结果分析

5 结束语






