建筑幕墙安装机器人的力控制分析
苑冶
沈阳远大铝业工程有限公司 辽宁沈阳 110000
建筑幕墙作为建筑物的主导性外围装饰品,越来越受到人们青睐,大量室外高空幕墙的安装工程为我国建筑装饰业带来新的发展契机。
1 幕墙安装机器人模型及控制研究模型
1.1 机器人运动学正解
根据D-H法则,采用后置坐标系法,机器人结构简图及各关节坐标系如图1所示。各连杆坐标系建立后,可以通过各坐标系之间的平移、旋转来计算n-1系与n系间的变换关系,该变换过程可用一个总的变换矩阵An来表示连杆n的齐次变换矩阵

图1 幕墙安装机器人实体图

将各个坐标系间的转换矩阵相乘便可以得到从基坐标系O0到机器人末端坐标系O8的转换矩阵08T:
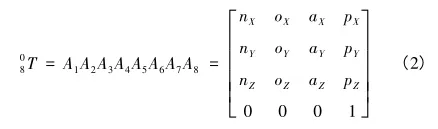
根据三角形的正弦定理和余弦定理求得:

同理可得到关节θ6的求解方法,由此得到了幕墙安装机器人各个电机处的旋转位移变量(θ1,θ2,θ3,θ5,θ6,θ7)与机器手末端位姿矩阵[n,o,a,p]之间的关系。
1.2 阻抗控制研究模型的建立
在仿真分析时,对关节2和关节3进行研究。依据所建的阻抗模型,认为各连杆质量均匀分布且后面的4~6轴位姿不变。
令L=a4+a5+a6+a8则研究模型的运动学方程为:
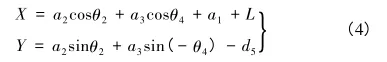
采用牛顿-欧拉递推方法,记:τ=(τ2,τ3)T,q=(θ2,θ3)T,得到关节空间中的动力学模型:
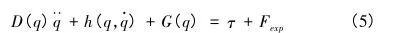
式中:D(q)为惯性矩阵,h(q,q·)为离心力和哥里奥利力矢量,G(q)为重力矢量,表达式为:

大臂和小臂的质量m2和m3分别为:m2=39.431kg,m3=25.478kg。a1=0.090m,a2=1.080m,a3=0.640mL=a4+a5+a6+d8=0.4121m 将以上的数学方程及参数,带入到阻抗控制仿真模型。
2 幕墙安装机器人工作空间分析
蒙特卡洛(MonteCarlo)方法是较常用的数值方法之一,方法步骤如下:(1)求解机器人运动学方程,得到机器人末端位姿。(2)机器人的每个关节变量都有自己的取值范围,将每个关节的取值范围均匀的选取n个随机数。例如,机器人的第一关节θ1,首先在0—1范围内生成n个随机数,以α1,…,αn表示,然后根据θ1的取值范围。机器人的其他关节变量做同样处理。(3)将上一步得到的机器人各关节变量的n组数值代入到第一步求解的运动学方程中去,即可以得到机器人各关节变量和机器人末端相对于基座坐标的一一映射。由机器人末端执行器所达到的这些随机点就构成了机器人工作空间的云图。利用LabVIEW的计算仿真和绘图能力,据MonteCarlo求解机器人工作空间的步骤,首先根据幕墙安装机器人运动学方程,求解运动学正解,得到末端的目标位置坐标。
然后利用LabVIEW中的“随机数VI”和“For循环”产生n个大于0小于1的随机数,记作R andk(k=1,2,…,n),由此每个运动关节产生一个随机步长:
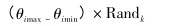
进而得到每个关节的随机值
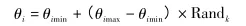
式中:i代表关节,i=1,2,3,4,5,6;R andk代表计算机产生的大于0小于1的随机数,k=1,2,…,n。n代表产生随机数的个数,在这里n取100,即幕墙安装机器人每个关节随机产生100个位姿。最后将机器人的每个轴所产生的n个随机数值代入到机器人的运动学正解中去,得到机器人末端的位置向量,并将向量端点显示在笛卡尔坐标系中。运行LabVIEW程序得到幕墙安装机器人工作空间三维点图,如图2所示。
3 结语

图2 幕墙安装机器人工作空间
综合分析幕墙安装的非结构环境与安装过程中的随机性问题,结合目前建筑机器人的研究成果分析,采用接触式人机协作的安装方式实现幕墙的安装工作是当前较合适的施工方式。

