考虑激电效应和电磁效应的复电阻率法 二维数值模拟研究

张志勇，刘固望，谭捍东，腰善丛，黄　笑，付振兴

(1.核工业北京地质研究院 中核集团铀资源勘查与评价技术重点实验室，北京 100029；2.中国地质科学院矿产资源研究所国土资源部成矿作用与资源评价重点实验室，北京 100037；3.中国地质大学(北京)地球物理与信息技术学院，北京 100083；4.核工业二四三大队，内蒙古 赤峰 024000)

复电祖率实测数据是包含激电效应和电磁效应的影响，而传统的复电祖率法二维数值模拟只考虑激电效应会影响后续资料处理结果的精度，因此本文开展同时考虑激电效应和电磁效应的复电祖率法二维正演研究。本文正演是基于二次场满足的麦克斯韦方程组，通过傅里叶变换将其变换到波数域，结合有限单元法，引入Cole-Cole模型，形成正演矩阵方程，采用超松弛迭代双共轭梯度法求解该方程组可得波数域结果，再由反傅里叶变换将其转换至空间域，完成了正演研究。然后通过几个模型算例的计算验证了该算法的正确性，也为复电阻率法二维反演奠定了基础。

复电阻率法；有限单元；Cole-Cole模型；数值模拟；电磁效应

复电阻率法的物质基础是岩石、矿石的电化学性质差异，通过在地面观测大地的频谱，从而达到寻找电性异常体的目的[1]。相对其他电法分支方法，复电阻率法有以下优点：①该方法能得到的电性参数较多，结合这些参数的对比解释能提供更丰富的地电信息；②采用轻便的采集装备，方便其在地形复杂地区开展工作。目前，复电阻率法已广泛应用在固体矿产勘探[2-4]、水文地质[5]、油气资源[6]、监测环境[7]、工程地质[8]等方面。因此，研究复电祖率法正演有一定的实际应用价值。

国内外许多学者做了关于复电祖率法数值模拟方面的工作。Loke等完成了复电阻率法二维正反演，其未考虑电磁效应而仅仅考虑了激电效应，其反演的电阻率和极化率初始模型是由一种近似反演方法获取[9]。国内，徐凯军[10]、蔡军涛等[11]、杨晓弘等[12]、赵广茂[13]、尚晓[14]、尹成芳等[15]、张志勇等[16]都是基于泊松方程，完成了电阻率分块均匀、网格剖分为三角形或四边形的复电阻率法二维有限元数值模拟。范翠松等[17]、欧鸥[18]分别研究了复电阻率法二维正反演。

本文复电阻率法二维正演是基于二次场满足的麦克斯韦方程组，经过傅里叶变换将其变换到波数域，结合有限单元法，形成正演矩阵方程，同时考虑激电效应和电磁效应，将大地的实际电阻率由Cole-Cole模型定义得到的复电阻率替换，该方程采用超松弛迭代双共轭梯度法求解，再由反傅里叶变换得空域结果，二维正演完成。

1　复电祖率法二维正演

1.1　二维数值模拟

本文采用的地电模型如图1所示，其中y轴为构造走向方向，假定其电性参数仅仅在x-z是变化的，而在走向方向是恒定无变化的。

图1　地电模型示意图

假设时间因子是eiωt，忽略位移电流的影响，二次场满足的麦克斯韦方程组，见式(1)。

(1)

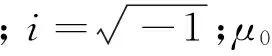
傅里叶变换，见式(2)。

(2)

式中：^为波数域的值；ky为波数值。

对式(1)沿着走向方向进行傅里叶变换，可将其从空间域变换到波数域，整理后得式(3)～(8)。

(8)

求解式(5)和式(6)，得式(9)和式(10)。求解式(3)和式(8)，得式(11)和式(12)。

(10)

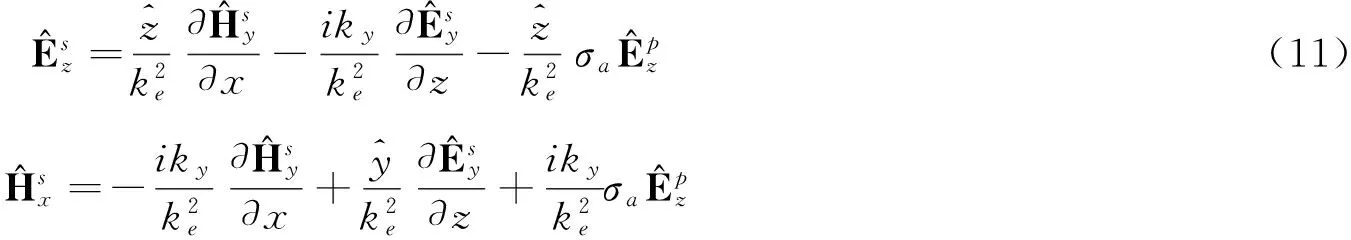
(12)

将式(9)和式(11)代入式(4)，可得式(13)。将式(10)和式(12)代入式(7)，可得式(14)。

(14)

1.2　有限单元法分析

结合有限单元法[19]中四节点的等参单元法推导，对式(13)和式(14)应用伽里金法、格林公式，且正演中边界条件为第一类边界条件(也即是电磁场分量在边界网格上的值都为零)，得到二次场满足的电磁场有限单元法计算公式，见式(15)和式(16)。

(16)

经过单元分析，将式(15)和式(16)写为式(17)。

(17)

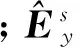
k1(i,j)=

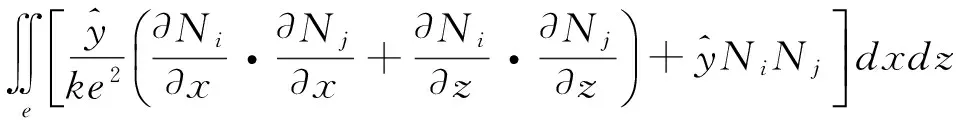
(18)

k2(i,j)=

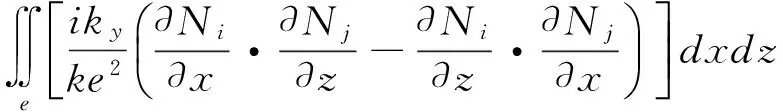
(19)

k3(i,j)=

(20)

k4(i,j)=

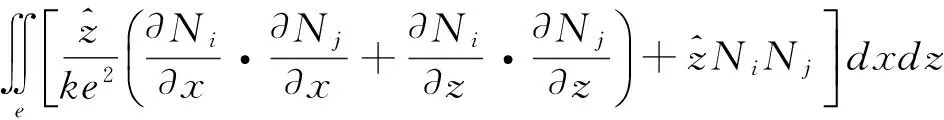
(21)

s1(i)=

(23)

为求解正演矩阵方程(式(17))，要先得到方程右端项S中的波数域一次电场分量。而其可以参考电磁法理论[20]进行推导，得到式(24)[21]。

(24)

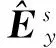
1.3　稀疏矩阵的存储

式(17)中系数矩阵K是稀疏且对称的，全部存储K矩阵需要的内存较大。由于矩阵K每行的非零元素个数有限，因此可采用按行压缩(CSR)方式将其进行存储(表1)，这样不仅减少内存占用量，而且便于使用共轭梯度法来求解方程组。

假设K为N×N的稀疏且对称矩阵，采用按行压缩的方式存储，矩阵K的存储可用一维数组P、IP、JP进行。K中每行非零元素值依次存放在数组P中；数组IP共有N+1个元素，每行首个非零元素在数组K中的位置存放在前N个数中，非零元素总数加1等于第N+1个数；K中每行非零元素所在列号存放在数组JP中。假设稀疏矩阵M如下所示。

表1　CSR存储格式表

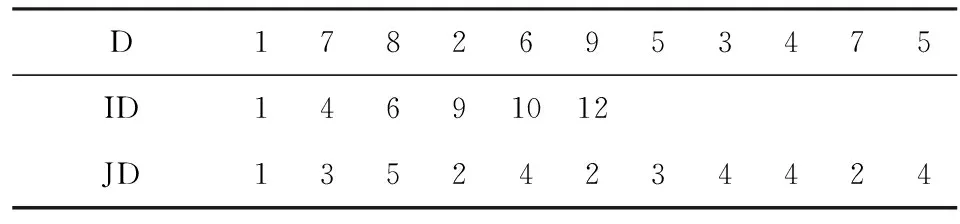
D17826953475ID14691012JD13524234424

1.4　Cole-Cole模型

为同时考虑激电效应和电磁效应，正演数值模拟时大地的实际电阻率由Cole-Cole模型定义的复电阻率来替换。1978年，Pelton等通过研究总结出可以用Cole-Cole模型来表征均匀岩石、矿石的复电阻率频谱，见式(25)[22]。

(25)

式中：ρ(iω)为复电阻率；c为频率相关系数；m为极化率；ρ0为零频电阻率；τ为时间常数。

1.5　正演基本流程

图2为正演流程图。

2　模型计算

通过分别设计层状模型、二维模型来验证本文二维数值模拟程序的正确性，将其计算结果分别与Kerry Key的1DCSEM程序[23]、Kerry Key的2DCSEM程序[24]计算结果进行对比。下面两个算例中，沿x轴水平方向放置发射源，且位于x=y=z=0处，从x=50 m到x=1 000 m放置25个接收点，频率f为8 Hz、16Hz、32 Hz。

2.1　层状模型

如图3所示，在背景电阻率为100 Ω·m的地下介质中存在电阻率为110 Ω·m，厚度为100 m的低阻层，低阻层顶界面埋深为120 m。将计算结果与Kerry Key的1DCSEM计算结果进行对比验证。图4中，1DCSEM计算结果用圆圈表示，而本文程序计算结果用点表示，电场分量Ex实部曲线、虚部曲线基本吻合，说明本文有限单元数值模拟算法的正演结果正确。

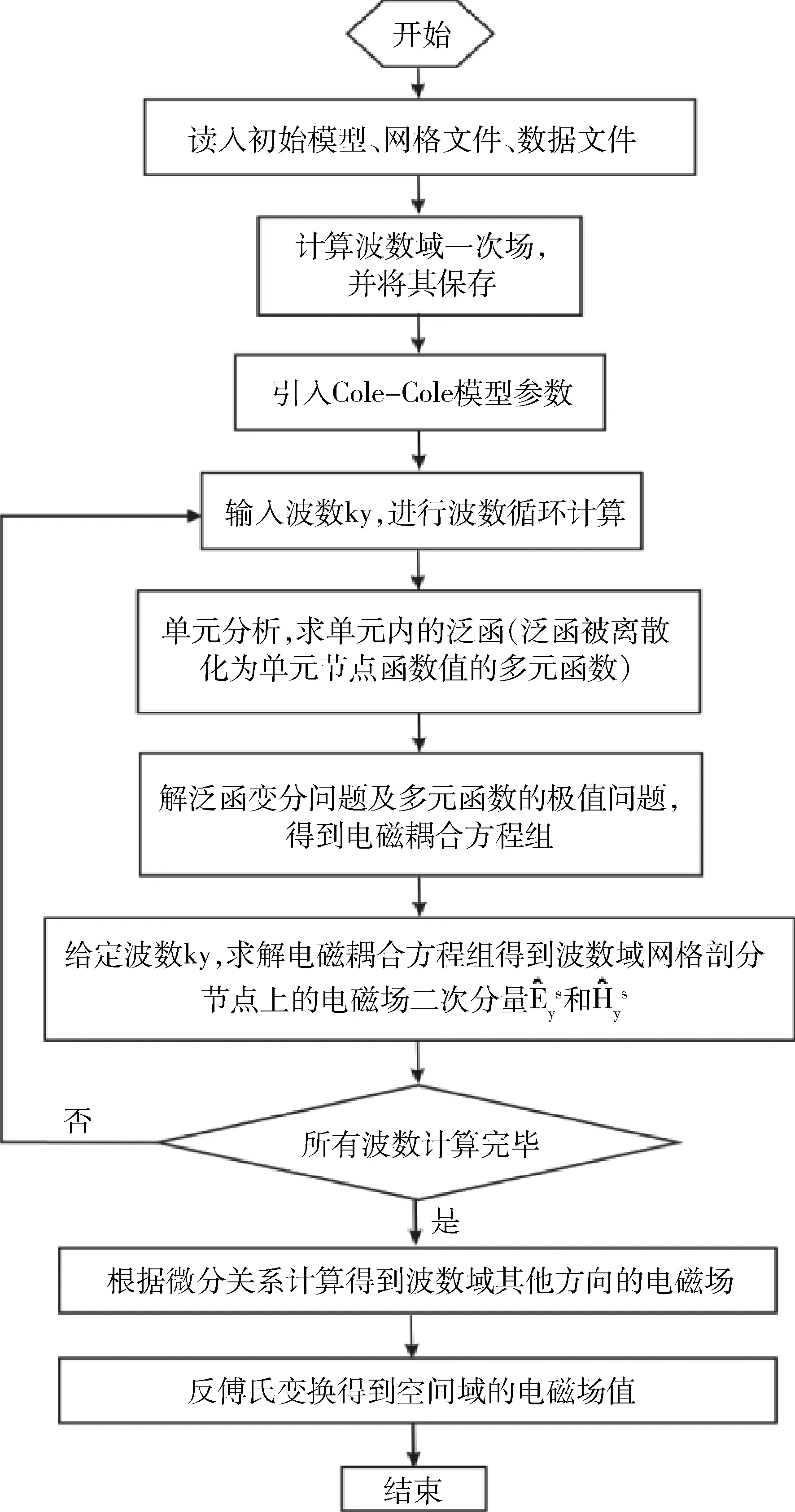
图2　正演流程图

图3　层状模型

2.2　二维棱柱体计算结果对比

如图5所示，在背景电阻率为100 Ω·m的地下介质中存在电阻率为10 Ω·m的二维棱柱体，其顶界面埋深为120 m， 长200 m，厚100 m。分别采用

图4　层状模型计算结果对比图

图5　二维模型

Kerry Key的2DCSEM和本文开发的程序对该模型进行计算， 其计算结果如图6所示。2DCSEM计算结果用圆圈表示，本文程序计算结果用点表示，电场分量Ex实部曲线、虚部曲线基本吻合，说明了本文开发的有限单元数值模拟算法正确。

3　结　论

本文基于有限单元法中四节点的等参单元完成了既考虑电磁效应又考虑激电效应的复电阻率法二维数值模拟。基于二次场满足的麦克斯韦方程组，通过傅里叶变换得到麦克斯韦方程组波数域形式，结合有限单元法，推导出正演矩阵方程，为考虑激电效应，引入Cole-Cole模型，且应用第一类边界条件，该方程组由超松弛迭代双共轭梯度法来求解，将该波数域结果由反傅里叶变换变换到空间域。正演矩阵方程中的大型稀疏矩阵采用按行压缩存储，大大降低了内存占用量。最后，通过采用Kerry Key公开的程序与本文开发的程序对理论模型进行试算，验证了本文正演程序正确、可靠。

图6　Ex实虚部对比曲线

[1]杨进.环境与工程地球物理[M].北京:地质出版社,2011.

[2]杨振威,严加永,陈向斌.频谱激电法在安徽沙溪斑岩铜矿中的应用[J].地球物理学进展,2013,28(4):2014-2023.

[3]曹蔚杰,单明良,高勇,等.复电阻率法(CR)在铜钼矿勘查中的应用效果[J].工程地球物理学报,2014,11(2):203-207.

[4]徐自生,张丽,唐伟,等.复电阻率法(CR)在内蒙古那吉河铅锌矿探测中的应用[J].矿产勘查,2015(2):165-170.

[5]REVIL A,KARAOULIS M,JOHNSON T,et al.Review:Some low-frequency electrical methods for subsurface characterization and monitor in hydrogeology[J].Hydrogeology Journal,2012,20(4):617-658.

[6]许传建,徐自生,杨志成,等.复电阻率(CR)法探测油气藏的应用效果[J].石油地球物理勘探,2004(zk):31-35.

[7]FLORES Orozco A,KEMNA A,OBERDÖRSTER C,et al.Delineation of subsurface hydrocarbon contamination at a former hydrogenation plant using spectral induced polarization imaging[J].Journal of Contaminant Hydrology,2012,136-137:131-144.

[8]BREEDE K,KEMNA A,ESSER O,et al.Spectral induced polarization measurements on variably saturated sand-clay mixtures[J].Near surface geophysics,2012,10(6):479-489.

[9]LOKE M H,CHAMBERS J E，OGILVY R D.Inversion of 2D spectral induced polarization imaging data[J].Geophysical Prospecting,2006,54(3):287-301.

[10]徐凯军.2.5维复电阻率电磁场正反演研究[D].长春:吉林大学,2007.

[11]蔡军涛,阮百尧,赵国泽,等.复电阻率法二维有限元数值模拟[J].地球物理学报,2007,50(6):1869-1876.

[12]杨晓弘,何继善,童孝忠.频率域激电有限元数值模拟[J].地球物理学进展,2008,23(4):1186-1189.

[13]赵广茂.带地形的复电阻率2.5维电磁场正反演研究[D].长春:吉林大学,2009.

[14]尚晓.起伏地形条件下2.5维CR有限元数值模拟研究[D].北京:中国地质科学院,2012.

[15]尹成芳,柯式镇,张雷洁.复电极型复电阻率扫频系统响应数值模拟[J].测井技术,2014,38(3):273-278.

[16]张志勇,周峰.复电阻率2.5D有限单元法正演[J].地球物理学进展,2014,29(5):2326-2331.

[17]范翠松,李桐林,严加永.2.5维复电阻率反演及其应用试验[J].地球物理学报,2012,55(12):4044-4050.

[18]欧鸥.起伏地形条件下2.5维复电祖率法数值模拟与反演成像研究[D].成都:成都理工大学,2015.

[19]徐世浙.地球物理中的有限单元法[M].北京:科学出版社,1994.

[20]NABIGHIAN M.N.Electromagnetic Methods in Applied Geophysics[R].vol.1:Theory.Society of Exploration Geophysicists,1988.

[21]LU X Y.Inversion of Controlled-source Audio-Frequency Magnetotelluric data[D].Seattle：University of Washington,1999.

[22]PELTON W H,WARD S H,HALLOF P G,et al.Mineral discrimination and removal of inductive coupling with multifrequency IP[J].Geophysics,1978,43(3):588-609.

[23]KEY K.1D inversion of multicomponent,multifrequency marine CSEM data:Methododology and synthetic studies for resolving thin resistive layers[J].Geophysics,2009,74(2):F9-F20.

[24]KEY K，OVALL J.A parallel goal-oriented adaptive finite element method for 2.5-D electromagnetic modeling[J].Geophysical Journal International,2011,186(1):137-154.