基于3DEC对某输电线路新建铁塔岩质边坡的稳定性评价

赵　健，杨　立，邓冬梅，张　健，邓　姗

( 1.贵州电力设计研究院，贵州 贵阳 550002；2.中国地质大学(武汉) 工程学院，湖北 武汉 430074 )

电力行业一直是我国经济建设的重要产业，在我国广泛分布的山区不时会遇到将输电线塔建立在危险陡坡的情形，边坡稳定性成为输电线路建设中的关键突出问题。同时，开挖陡坡势必会带来新的边坡问题，由于输电线塔具有结构高、跨度大等特点，铁塔荷载与风荷载会威胁到线路安全，因此研究塔基边坡的稳定性具有重大的工程意义。

岩质边坡发育层面，并被节理裂隙切割。据基于运动学的边坡稳定性分析可知，岩质边坡的变形破坏主要受控于临空面与结构面的空间关系，岩体可能沿单一不连续面滑动、开挖面崩落或形成楔形体沿结构面交线滑动[1]。由于岩体变形和破坏具有复杂性，因此全面分析边坡的岩性特征、优势结构面及其组合可能造成的边坡破坏模式是稳定性评价的关键。

岩质边坡稳定性分析方法可分为定性和定量两类，定性分析方法主要包括自然历史分析法、图解法、专家系统法等，定量分析方法主要有极限平衡分析法、数值分析法、可靠度方法、模糊综合评价法等。在定性分析方法中，边坡结构面极射赤平投影法是一种简便而有效的图解分析方法，该方法假定岩体为刚性且忽略软弱夹层和条件力的作用[2]，利用结构面极射赤平投影技术直观地反映边坡结构面组合关系、结构面组合切割体与边坡的相对关系、不利切割体的潜在滑动方向等[3]，在评价边坡稳定性方面具有突出的优势[4]，已经被广泛应用于实际边坡工程潜在破坏模式的分析中，如吴绍强[5]、李才等[6]利用结构面极射赤平投影技术分析了岩质边坡结构面组合下可能的边坡破坏模式。在定量分析方法中，数值模拟方法主要用于研究岩土工程活动对附近环境的影响以及岩体-支护结构力学行为的模拟[7]，目前常用的方法是有限元法、边界元法、有限差分法、离散元法、不连续变形分析法、流形元法等。其中，有限元法基于最小总势能变分原理[8]，将连续体近似为多个彼此相联系的单元体组成的物理模型，能够方便地处理各种非线性问题，是目前应用最广且较为成熟的研究岩体性质的方法，但其缺点是难以模拟复杂裂隙网络的岩体；而离散元方法能够很好地模拟岩体等非连续介质的力学行为，是一种非连续数值分析方法，在处理不连续介质问题中有较大的优势[9-10]，目前已开发了众多基于离散元方法的模拟软件，其中由美国Itasca集团的3DEC(3-Dimensional Distinct Element Code)软件允许岩体系统大变形和大位移，已在许多岩质边坡稳定性研究中使用。近年来，强度折减法已较普遍地应用于边坡稳定性评价中，强度折减法就是在边坡稳定性计算过程中，用折减系数逐步降低岩土体强度参数(黏聚力和内摩擦角)，反复计算至边坡达到临界破坏状态，此时的强度指标与原强度指标之比，即边坡的稳定性系数[11-12]。基于强度折减的3DEC离散元方法被认为是不连续岩质边坡稳定性分析的有力工具[13-14]。

基于上述研究，本文以某塔基边坡为例，因距离高层住宅楼小区较近，已采用锚索加固，边坡处于稳定状态，但由于城区输电线路规划需在该边坡中部新建铁塔，将会开挖边坡并截断锚索，势必对边坡原有稳定性状态造成影响。因此，为评价该塔基边坡受到工程活动影响下的稳定性，本文在现场调研与结构面测绘的基础上，确定边坡岩体优势结构面，采用极射赤平投影法分析塔基边坡潜在的破坏模式，并通过3DEC离散元模型，进一步定量评价开挖并截断锚索后塔基边坡的稳定性以及新增支护并新建铁塔后边坡的稳定性。

1　塔基边坡的潜在破坏模式分析

1. 1　塔基边坡的基本地质条件

本文拟研究的塔基边坡高约40 m，为陡倾角层状切向坡，基岩部分外露，坡顶有部分第四系覆盖物，塔基边坡下伏基岩以二叠系中统吴家坪组(P2w)强风化泥岩、互层状泥岩和灰岩以及强-中风化灰岩为主，边坡排水设施较为完善。该塔基边坡呈3个平台，上部已有2个运营中的铁塔(铁塔1和铁塔2)，因小区建设，边坡中下部已采用锚索支护。既有铁塔、开挖设计面、拟建铁塔及塔腿位置，详见边坡剖面图1。

图1　岩质边坡工程地质剖面图Fig.1　Engineering geological profile of the rock slope

1. 2　塔基边坡的潜在破坏模式分析

据边坡工程地质测绘，拟研究的塔基边坡坡面产状为151°∠45°，层面(J1)产状为213°∠43°，充填物为泥膜。经过测量并统计得到该塔基边坡岩体5组优势结构面，结构面平直、较光滑，充填物为泥膜，岩体被节理切割成碎裂状，岩体结构面参数见表1。

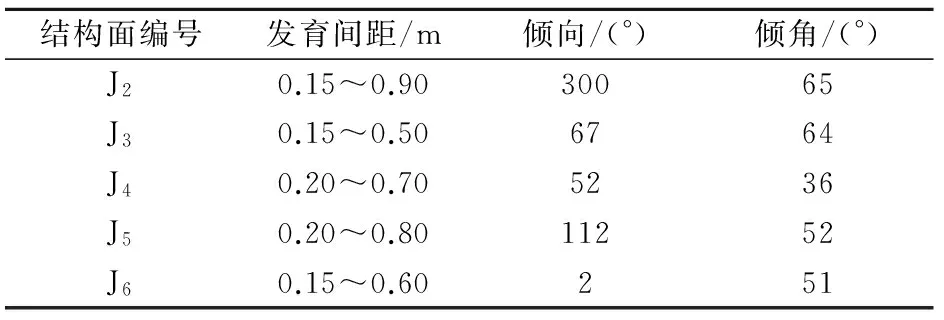
表1　某塔基边坡的岩体结构面参数Table 1　　　　Structure plane parameters of the rock slope of a tower foundation

综合该塔基边坡的岩性特征、坡面产状、层面产状和节理面产状，得到边坡结构面下半球极射赤平投影图(见图2)，据此可分析该岩质边坡的潜在破坏模式。

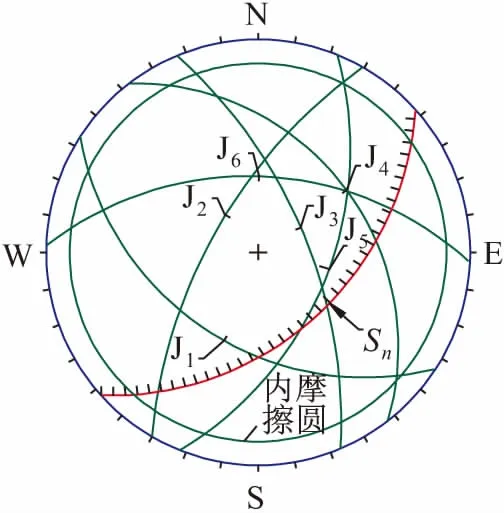
图2　某塔基边坡结构面赤平投影图Fig.2　　　　Stereographic projections of the slope structure plane of a tower foundation

(1) 平面滑动模式。岩质边坡发生平面滑动需要同时具备以下条件：①结构面倾角θ大于结构面摩擦角φj而小于坡角α；②结构面的倾向与边坡面倾向相同；③边坡中存在侧向切割面[2]。本案例中塔基边坡强风化泥岩内结构面内摩擦角难以试验获得，取经验值10°，按上述条件分析边坡能否产生平面滑动，见表2。由表2可知，该塔基边坡发生平面滑动的可能性较小。

表2　边坡平面滑动模式分析Table 2　Analysis of plane slide failure mode of the slope

(2) 楔形体滑动模式。岩质边坡发生楔形体滑动需要具备以下2个条件：①结构面交线倾伏角δ大于结构面摩擦角φj而小于坡角α；②结构面交线倾伏向与边坡面倾向相同[2]。本案例中塔基边坡坡面产状为151°∠45°，统计两两结构面组合的交线产状，据此对边坡破坏模式分析如下：①(J1,J2)、(J3,J5)结构面交线的倾伏角大于坡角，楔形体不具备可能滑动的临空条件，边坡发生楔形体滑动的可能性小；②(J1,J3)、(J1,J4)、(J1,J5)结构面交线倾伏向与边坡面倾向相同，夹角较小，结构面交线倾伏角小于边坡面倾角而大于结构面摩擦角，边坡有沿着该结构面组合发生楔形体滑动的可能；③其余9组结构面组合的交线倾伏向与边坡面倾向呈大角度相交，边坡沿这些结构面发生楔形体滑动的可能性小。按上述条件综合两组结构面组合切割下该塔基边坡可能发生楔形体滑动破坏模式的分析,详见表3。

(3) 圆弧形滑动模式。由于本案例中塔基边坡上部强风化泥岩层较厚且岩体风化破碎，岩土体性质

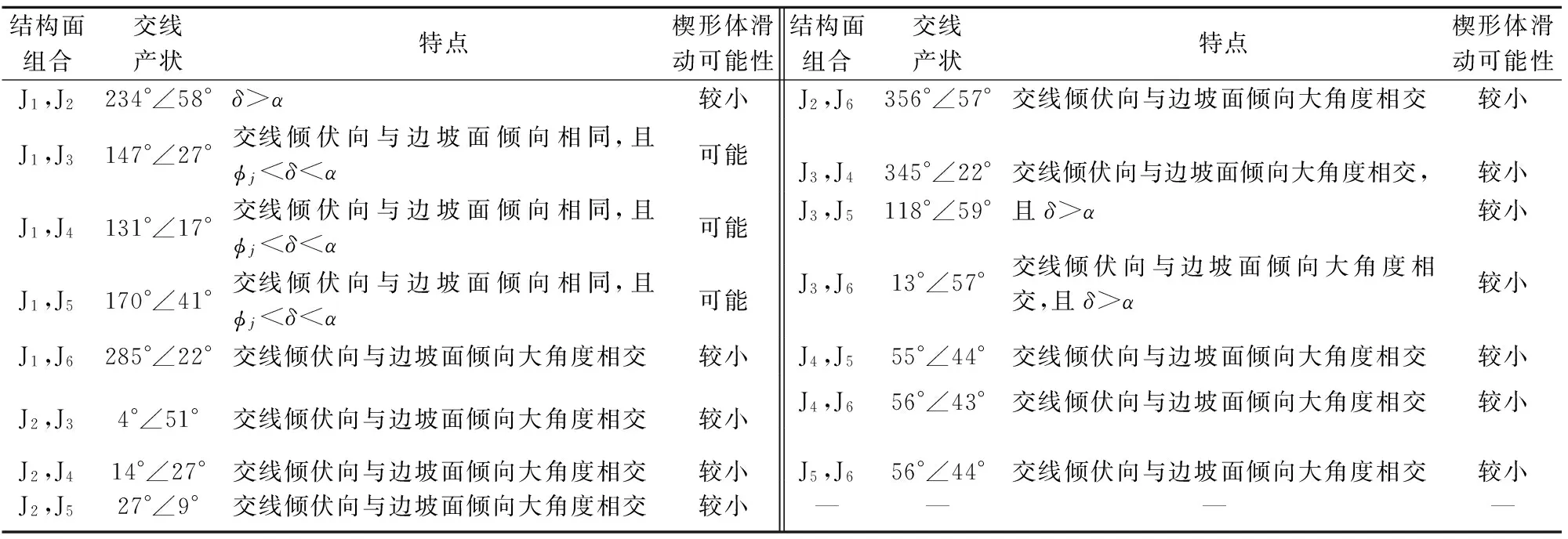
表3　两组结构面组合切割下塔基边坡的潜在破坏模式分析Table 3　Analysis of potential failure mode of the slope in different combinations by two sets of joints

较差，可能在边坡泥岩层发生圆弧形滑动破坏模式。

综上所述，该塔基边坡发生平面滑动的可能性较小，但可能发生楔形体滑动和圆弧形滑动。

2　塔基边坡的稳定性评价

2. 1　计算模型与参数

根据该塔基边坡空间特征，建立76 m×50 m×58 m的边坡模型，模型地层材料为强风化泥岩、互层状泥岩和灰岩、中风化灰岩。由上述赤平投影分析可知，该塔基边坡潜在的楔形体滑动破坏模式主要是由于(J1,J3)、(J1,J4)、(J1,J5)三组结构面控制，因此在模型中输入层面以及J3、J4和J5结构面来对岩体进行切割，而考虑圆弧形滑动破坏模式情形时，在模型中只输入层面进行控制。该塔基边坡岩体结构面间距由钻孔揭露和实测间距平均值确定，结构面物理力学参数取相同值，根据室内试验，参考相关规范确定出研究边坡岩土体的物理力学参数及结构面力学参数，详见表4和表5，边坡锚索主要参数见表6，并设置顶部两塔荷载为塔基范围内的均布荷载(q=25 kPa)。

表4　模型地层材料物理力学参数Table 4　Physical and mechanics parameters of the model strata materials

表5　岩质边坡结构面力学参数Table 5　　　　Mechanics parameters of the structural plane of the rock slope

表6　塔基边坡锚索主要参数Table 6　Major parameters of the anchor cable

根据《建筑结构荷载规范》(GB 5009—2012)中的风荷载计算公式[15]，垂直作用于塔架表面上单位面积的风荷载标准值按下式计算：

ωz=βzμsμzω0

(1)

式中:ωz为作用在高耸结构高度处单位面积上的风荷载标准值(kN/m2);βz为风振系数;μs为风荷载体型系数;μz为风压高度变化系数;ω0为基本风压(kN/m2)。

根据《建筑结构荷载规范》(GB 5009—2012)，公式(1)中各参数取值见表7，得到铁塔1、铁塔2和拟建铁塔的风荷载分别为0.72 kN/m2、0.66 kN/m2和0.58 kN/m2，铁塔线路方向与塔基边坡走向相同，并按最不利方向施加到铁塔表面。

设置模型边界条件为：模型的底面处施加竖向固定约束，模型的侧面处施加水平固定约束，模型顶面为自由无约束，选择莫尔-库仑屈服条件的弹塑性模型进行计算。岩土体等材料均采用Zone单元进行模拟，锚索采用Cable单元进行模拟，模型共用65 532个Zone单元，195根Cable单元。建立的截断锚索前边坡两种潜在破坏模式下的计算模型，见图3和4。

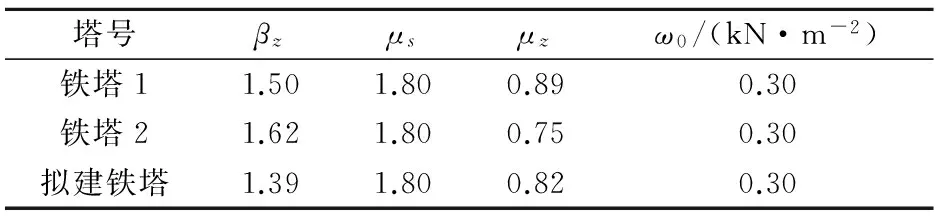
表7　风荷载计算参数Table 7　Parameters in wind load

图3　截断锚索前边坡楔形体滑动破坏模式下的计算模型Fig.3　　　　Calculation model of the slope in wedge slide failure mode before cutting cables

图4　截断锚索前边坡圆弧形滑动破坏模式下的计算模型Fig.4　　　　Calculation model of the slope in circular slide failure mode before cutting cables

2. 2　开挖并截断锚索后塔基边坡的稳定性分析

在开挖边坡截断部分锚索情况下，经过3DEC迭代计算出天然工况下该塔基边坡的稳定性系数分别为0.84(楔形体滑动)、0.874(圆弧形滑动)，表明天然工况下的边坡稳定性系数已经无法满足工程安全性要求。结合圆弧形滑动破坏模式下开挖边坡的位移模拟结果(见图5)可以看出：在天然状态下开挖边坡的最大位移接近1.3 m，这也从另一方面说明未支护进行开挖的塔基边坡发生失稳破坏的可能性大。由此可见，该塔基边坡在无支护情况下开挖将会产生破坏，在实际工程开挖之前必须采取有效支护措施以确保边坡的稳定。

图5　圆弧形滑动破坏模式下开挖边坡的位移云图Fig.5　　　　Slope displacement by excavation in circular slide failure mode

2. 3　支护补偿并新建铁塔后塔基边坡的稳定性分析

结合该塔基边坡已支护状况，天然工况下边坡的稳定性系数为1.25，暴雨工况下边坡的稳定性系数为1.05，采用桩体将塔基荷载传递到潜在滑动面以下岩体，起到抗滑桩的抗滑作用；同时，在开挖位置按截断1根锚索补2根锚索的方式补偿加固，新增锚索深入到已有锚索深度以下，设置于既有锚索中部，避开桩位，并在桩顶新增预应力锚索以平衡铁塔水平风荷载，锚索的倾角为25°，与岩层夹角为49°，平均间距为2 m×2 m。新建铁塔荷载形式为均布荷载，按塔基面积计算得到q=35 kPa,塔基边坡抗滑桩的主要参数见表8，支护后的塔基边坡模型见图6。

经过3DEC对该模型的迭代计算，得出楔形体滑动破坏模式下边坡天然工况时的稳定性系数为1.225，暴雨工况时稳定性系数为1.063，圆弧形滑动破坏模式下天然工况时的稳定性系数为1.246，暴雨工况时稳定性系数为1.097，说明该塔基边坡处于基本稳定状态；同时，可以得到支护后两种破坏模式下开挖边坡的位移云图(见图7和图8)。

表8　岩质边坡抗滑桩的主要参数Table 8　　　　Major parameters of anti-sliding piles of the rock slope

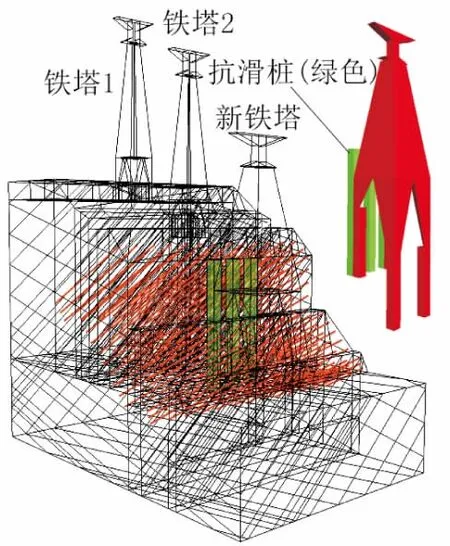
图6　支护后的塔基边坡模型Fig.6　Model of the supported slope of tower foundations

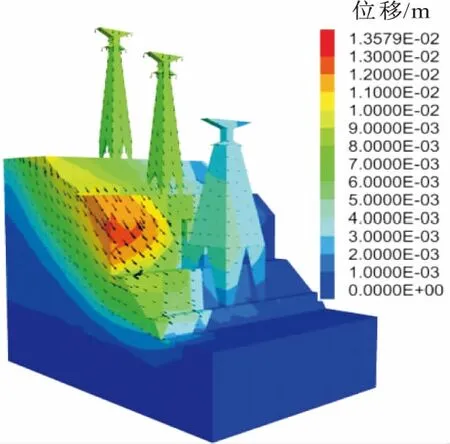
图7　支护后楔形体滑动破坏模式下开挖边坡的位移云图Fig.7　　　　Slope displacement fringe after supporting in wedge slide failure mode

图8　支护后圆弧形滑动破坏模式下开挖边坡的位移云图Fig.8　　　　Slope displacement fringe after supporting in circular slide failure mode

由图7和图8可见，在降雨工况下补偿锚索并设置抗滑桩之后新建铁塔，边坡开挖面附近变形得到控制，变形处于在施工允许范围之内。由此可见，在锚索和抗滑桩的作用下，该塔基边坡变形得到了有效控制，边坡处于基本稳定状态，支护方案能够满足工程安全性需要。

3　结　论

本文以塔基边坡为研究对象，采用极射赤平投影法分析边坡潜在的破坏模式，定性分析其稳定性，再通过3DEC离散元方法定量评价边坡的稳定性，可以得到以下结论：

(1) 工程地质分析与赤平投影分析表明，该输电线路边坡有沿着(J1,J3)、(J1,J4)、(J1,J5)发生楔形体滑动的可能，也有在强风化岩体中发生圆弧形滑动的可能。

(2) 通过3DEC数值模拟表明，该塔基边坡进行人工开挖后，其稳定性系数不满足工程安全性要求。因此该路基边坡开挖前须采取有效支护措施，以保证边坡的稳定。

(3) 在该路基边坡得到锚索及抗滑桩体系支护后，开挖边坡不会造成边坡大变形，边坡稳定性得到有效增强，处于基本稳定状态，满足工程安全性要求，其支护设计能够为类似工程提供参考。

参考文献：

[1] 宁宇,徐卫亚,郑文棠.应用离散元强度折减对复杂边坡进行稳定性分析[J].岩土力学,2007,28(S1):569-574.

[2] 唐辉明.斜坡地质灾害预测与防治的工程地质研究[M].北京：科学出版社,2015:160-161.

[3] 王鸣,黄鹏程,陈招军,等.基于GIS的岩质顺层边坡坡体组合类型空间分布[J].安全与环境工程,2017,24(4):47-51.

[4] 梁烨,王亮清,唐辉明.基于运动学分析的高切坡稳定性评价[J].安全与环境工程,2010,17(6):101-103,108.

[5] 吴绍强.极射赤平投影法在岩质边坡稳定性分析中的应用[J].西部探矿工程,2009,34(10)：117-119

[6] 李才,张行,黎艺明,等.深水河大桥桥墩边坡稳定性分析[J].安全与环境工程,2012,19(4):137-140,144.

[7] 蔡美峰.岩石力学与工程[M].北京：科学出版社,2013.

[8] 周维垣.高等岩石力学[M].北京：水利电力出版社,1990.

[9] 巨能攀,赵建军,黄润秋,等.基于3DEC的边坡块体稳定性分析[J].辽宁工程技术大学学报(自然科学版),2009,28(6):925-928.

[10]胡训健,卞康,葛云峰,等.基于PFC对含断续节理岩质边坡静力荷载下破坏形式的研究[J].安全与环境工程,2017,24(3):34-42.

[11]桂蕾,殷坤龙,翟月.基于FLAC3D模拟和强度折减法的滑坡稳定性计算[J].安全与环境工程,2011,18(6):9-14.

[12]熊文林.山区高速公路隧道洞口边坡稳定性的数值模拟[J].安全与环境工程,2013,20(5):108-112.

[13]雷远见,王水林.基于离散元的强度折减法分析岩质边坡稳定性[J].岩土力学2006,27(10):1693-1698．

[14]王清,陆新.用有限元强度折减法进行加筋土挡土墙稳定性分析[J].后勤工程学院学报,2006,22(1):63-66.

[15]中华人民共和国住房和城乡建设部.建筑结构荷载规范：GB 5009—2012[S].北京：中国建筑工业出版社，2012.