混合CHI和MI的改进文本特征选择方法

王 振，邱晓晖

(南京邮电大学 通信与信息技术学院，江苏 南京 210003)

0 引 言

随着信息技术的迅猛发展，网络上的数据呈现爆炸式的增长，而其中以文本数据居多。如何对众多的文本进行快速分类，成为了研究的热点，文本分类也由此产生并不断发展。文本分类是在给定类别的情况下，根据文本的内容，将其自动划分到一个或者几个预先给定的类别中[1]。文本分类主要由分词、预处理、特征选择、特性降维、分类算法、分类性能评估等几个步骤构成[2]。在构建特征向量时，如何降低向量的维数一直是需要解决的问题。因为一般大小的数据集经过提取就有上万个特征，大一点的数据集甚至能达到上百万个特征，这么高的维数不仅对计算产生了很大的负担，而且很多特征对分类而言都是无用的，还会降低分类的准确度。因此，可以通过特征选择方法，降低特征向量的维数，减少分类算法的运行时间，从而最终提高分类准确度。一直以来，特征选择问题都是研究的重点问题[3-5]。

目前，文本分类中常用的特征选择算法有文档频数(document frequency,DF)、卡方统计量(CHI-square statistic,CHI)、信息增益(information gain,IG)、互信息(mutual information,MI)、期望交叉熵(expected cross entropy,ECE)、文本证据权(weight of evidence for text,WET)等。美国卡内基梅隆大学的Yang教授对以上几种特征选择方法进行比较分析发现，CHI和IG方法的分类效果相对较好，但CHI方法相比IG方法的分类准确度更高[6]。因此，针对CHI的优缺点进行深入研究，探索该模型的改进途径对提高文本的分类准确度具有重要意义。近年来，很多研究者都对CHI进行了研究改进[7-9]。文中在分析传统CHI和MI方法的优缺点的基础上，通过引入词频并综合两种算法提出一种新的混合特征选择算法(CHMI)。

1 传统特征选择方法

1.1 传统卡方统计方法

卡方统计量来自一种假设检验的方法，在文本分类的特征选择问题中，用来表示特征t与所属类别c之间的相关度。特征t与类别c之间的相关度越大，其卡方统计值越大，该特征对于分类就越重要。假设特征t与类别c符合一阶自由度的卡方分布，t对于c的卡方统计量可由式(1)计算：

(1)

其中，A表示训练集中包含特征t且属于类别c的文档数；B表示训练集中包含特征t但是不属于类别c的文档数；C表示训练集中不包含特征t但是属于类别c的文档数；D表示不包含特征t且不属于类别c的文档数；N表示训练集中包含的文档总数，通常N固定不变且N=A+B+C+D，A+C表示属于类别c的文档数，B+D表示不属于类别c的文档数，这两个值对于确定的数据量来说都是常数，因此式(1)可以简化为：

(2)

当特征t与类别c相互独立时，AD-BC=0，根据式2可知χ2(t,c)=0。当AD-BC>0时，表示特征与类别正相关，相应的卡方统计值也越大，说明该特征与类别之间的相关度越强。

特征t对于整个训练集的卡方统计值通常有两种计算方式，加权平均和求最大值，计算公式分别如下：

(3)

(4)

其中，n为类别数。式(3)表示特征与所有类别的平均卡方值，式(4)表示特征与所有类别的卡方值的最大值。

1.2 传统的互信息方法

互信息的概念出自信息论[10]中，原本互信息用来衡量两个信号间的关联程度。在文本分类中，表现为特征与类别之间的关联程度。互信息的计算公式为：

(5)

用t表示特征，用c表示文本类别，则文本分类中的特征与类别之间的互信息计算公式为：

(6)

其中，p(t,c)表示文档包含特征t并且属于类别c的概率；p(t)表示包含特征t的文档在所有文档中的概率；p(c)表示属于类别c的文档占所有文档的概率。当特征t与类别c独立时，p(t,c)=p(t)p(c)，由式(6)可知特征与类别之间的互信息为0。p(t|c)值越大，特征与类别之间的关联性就越强，这样的特征就具有更多的分类信息；反之，特征与类别关联性就越弱，特征含有的分类信息也就越少。

特征t对于整个类别的互信息主要有两种计算方式，分别是互信息的最大值和各类别的互信息的平均值。通常，互信息的最大值比互信息的平均值的特征选择效果好。两种计算方式分别如下：

MImax(t)=maxiMI(t,ci)

(7)

(8)

2 改进的特征选择方法

2.1 传统CHI方法的不足与改进

传统CHI统计方法只考虑了特征词在所有文档集中出现的文档数量，而没有考虑特征词在某一篇文档中出现的次数，从而夸大了低频词的作用[11]。例如，现在一共有100篇文档，特征词t1在其中的90篇文档中均出现了一次，特征词t2在其中的60篇文档中均出现了50次，那么根据CHI公式计算得到CHI(t1,C)>CHI(t2,C)。CHI方法会倾向于选择特征词t1，但实际上特征词t2比特征词t1具有更多的分类信息，这是CHI方法的不足，会导致选择的特征不够准确，影响最终分类效果。针对CHI方法的这一缺陷引入词频因子α进行调节，α的计算公式为：

(9)

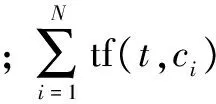
2.2 传统MI方法的不足与改进

传统的MI方法相比同样是信息论为基础的IG方法，更加直观且易于理解，计算复杂度也较低。MI方法的一个显著优点是考虑类内不同特征出现的频率，度量的是含有特征t的文本数与类别内总的文本数之间的比率，体现了不同类别内特征对类别的表现能力，有效地利用了文本的类别信息。但是MI方法也存在一些不足之处，一个主要的缺陷是没有考虑特征本身出现的频度，这会造成MI方法在评估特征时会倾向于选择一些低频特征[12]。

从式(6)可以看出，当两个特征的p(t|c)相同时，p(t)的大小决定互信息的大小，p(t)小则互信息大，但实际这样的特征含有的分类信息比较少，从而导致分类效果不理想。针对这个不足，提出在原有的公式中引入调节参数β，改进后的公式如下：

(10)

其中，β=p(t,c)，通过引入β，添加词频信息，适当增加中高频特征所占比重，降低低频特征的互信息值，避免互信息方法选择过多的低频特征，从而降低低频词对互信息方法的负效用。

不同类别之间，特征的词频也代表了不同的类别区分能力。一个区分能力强的特征词，应该集中分布在某些特定的类别中，也就是不同类别中的特征词频的方差应该尽可能大，这样的特征含有更多的类别区分信息[13]。为此，引入不同类别间特征的词频的方差对MI方法进行优化，记tfj(t)代表特征t在类别j中的频数，则方差可表示为：

(11)

其中，m表示总类别的数量。

那么式(10)可改进为：

(12)

2.3 改进的混合方法

文中提出混合CHI和MI两种特征选择方法，并对CHI和MI方法各自的不足进行了分析和改进，针对CHI方法不考虑词频的不足，引入词频调节因子α(t)。此外引入调节参数β减小MI方法对低频词的选择权重，引入类别间特征词频的方差γ对MI方法进一步优化，使MI方法选择那些集中分布在某些类别的特征，整合两种改进后的方法，得到一种混合的特征选择方法(CHMI)。该方法基于CHI和MI方法，选择那些集中出现在某些类别且在类别文本中分布均匀，出现次数较多的特征。

该方法的计算公式如下：

CHMI=χ2(t,c)×α×MI(t,c)×β×γ

(13)

3 实验结果与分析

为了验证该算法的有效性，将传统的CHI选择方法和传统MI选择方法与提出的混合方法进行比较，分类器选择实现简单、分类效果良好的朴素贝叶斯(NB)和最有效的分类算法之一的支持向量机(SVM)[14]。

3.1 数据集

实验数据集采用国际标准数据集20NewsGroup，共计20个类别，每个类别1 000篇文章，共计20 000篇文章。实验将其中的80%用于训练，20%用于进行分类准确度测试。

3.2 分类效果评估

在文本分类领域，评价一个分类算法好坏的主要指标有查准率(precision)，又称准确率，和查全率(recall)，又称召回率。除此之外，还有综合了查准率和查全率的Fβ值[15]。一篇文档的归属情况分为四种，具体见表1。

表1 文本分类归属判断

查准率是指分类器划分给某个类别的文本数量占真正属于该类别的文本数量的比例，其计算公式为：

(14)

查全率是指真正属于该类别的文本数量占分类器划分给该类别的文本数量的比例，其计算公式为：

(15)

Fβ值综合了查准率和查全率，通常其β值取1，其计算公式为：

(16)

3.3 实验步骤与结果

对数据集进行预处理，包括去除停用词、标点符号等，得到预处理后的特征集合。使用CHI、MI和CHMI三种特征选择方法对特征集合中的特征进行分类重要性计算，并对特征的分类重要性进行排序，得到排序后的特征集合。分类器采用朴素贝叶斯(NB)和支持向量机(SVM)。

图1表示的是经过改进后的CHI方法和改进后的MI方法与原CHI方法和原MI方法的分类准确度对比。图中CHI_2表示引入词频参数α(t)后的改进CHI方法，MI_2表示引入调节参数β和γ后的改进MI方法。从图中可以看出，引入词频的CHI_2方法比原有的CHI方法在分类准确度上有了一定提高，验证了词频参数提高CHI方法分类准确度的正确性。另外，引入调节参数后的MI_2方法比MI方法准确度也有了提高。

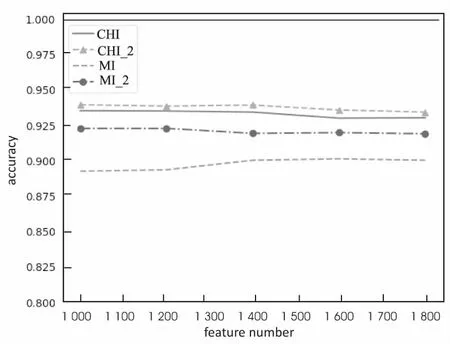
图1 改进后的CHI_2和MI_2与原CHI和MI的性能比较

图2显示的是NB分类器分别采用CHI、MI和CHMI三种特征选择方法在20GroupNews数据集上的分类准确度曲线。从图中可以看出，CHMI方法的分类准确度比CHI和MI方法都要高。MI方法准确度较低，但随着特征数量增加而变大。混合方法选择那些集中分布在某一类中，在类别中分布均匀的特征进行分类，最终分类效果比CHI和MI要好。

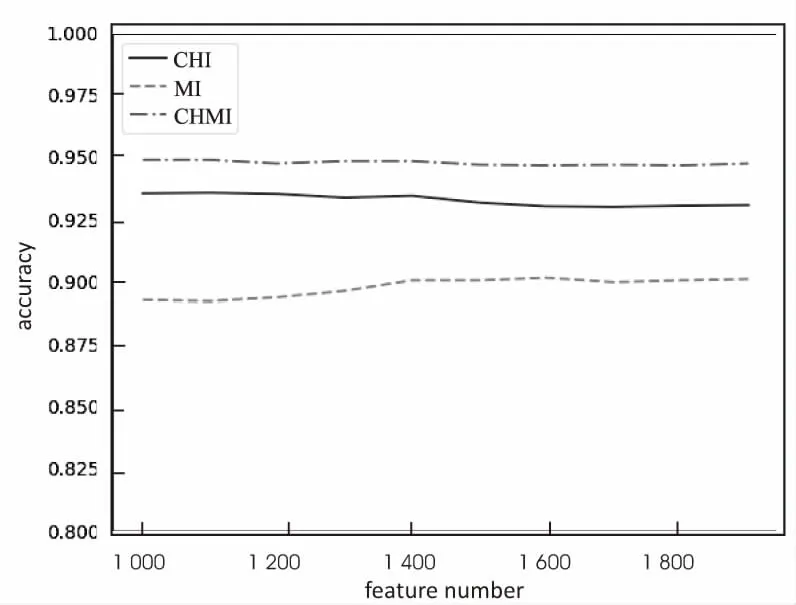
图2 三种特征选择方法的NB分类器性能比较

图3显示的是SVM分类器分别采用CHI、MI和CHMI三种特征选择方法在20GroupNews数据集上的分类准确度曲线。从图中可以看出，当特征数量为1 000时，CHMI方法的分类准确度明显高于CHI和MI方法。随着特征数量的增加，MI方法的分类准确度在增加，但依然低于CHMI方法。此外，SVM分类器的性能要优于NB分类器。

此外，衡量分类效果的另一个指标是F1值。采用贝叶斯分类器，三种方法的F1值具体情况如表2所示。从中可以看出，当特征比较小时，CHI和CHMI方法的F1值一样，当特征数量增大时，CHMI方法的F1值比传统的MI方法和CHI方法都要高。从查准率和F1值的结果看，CHMI方法的分类效果要好于传统的CHI和MI方法。

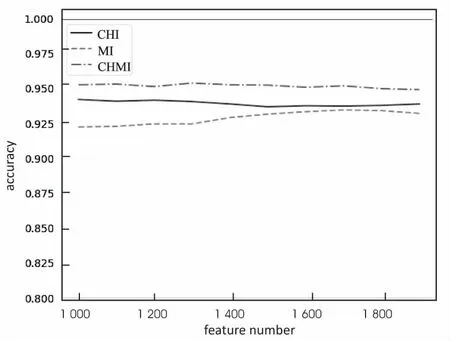
图3 三种特征选择方法的SVM分类器性能比较

表2 CHI方法、MI方法、CHMI方法的F1值比较

4 结束语

针对CHI方法不考虑词频的缺点，引入词频因子，考虑文档频的同时加入特征的词频，做特征选择时，选择在某个类别出现文档数量和词频数量都比较多的特征。MI方法因为倾向于选择低频词的缺点，特征数量小的时候效果较差。通过引入一个概率调节参数，降低选择低频词带来的负效用。另外考虑不同类别间特征的分布情况，引入类间词频方差，进一步优化MI方法。将两种改进后的方法结合，提出一种混合特征选择方法CHMI，选择集中出现在某一特定类并在该类中每篇文档中出现次数多的特征。实验结果证明，改进后的混合方法在分类准确度和F1值上相比传统的两种方法都有了提升。

参考文献：

[1] 苏金树,张博锋,徐 昕.基于机器学习的文本分类技术研究进展[J].软件学报,2006,17(9):1848-1859.

[2] 焦庆争,蔚承建.一种可靠信任推荐文本分类特征权重算法[J].计算机应用研究,2010,27(2):472-474.

[3] BIDI N,ELBERRICHI Z.Feature selection for text classification using genetic algorithms[C]//8th international conference on modelling,identification and control.[s.l.]:IEEE,2016:806-810.

[4] 林艳峰.中文文本分类特征选择方法的研究与实现[D].西安:西安电子科技大学,2014.

[5] 李军怀,付静飞,蒋文杰,等.基于MRMR的文本分类特征

选择方法[J].计算机科学,2016,43(10):225-228.

[6] YANG Y.An evaluation of statistical approaches to text categorization[J].Information Retrieval,1999,1(1-2):69-90.

[7] 樊存佳,汪友生,王雨婷.一种改进的CHI文本特征选择方法[J].计算机与现代化,2016(11):7-11.

[8] 裴英博,刘晓霞.文本分类中改进型CHI特征选择方法的研究[J].计算机工程与应用,2011,47(4):128-130.

[9] 闫 屹,张燕平,耿筱媛.基于CHI值特征选取和覆盖的文本分类方法[J].计算机技术与发展,2008,18(5):79-81.

[10] 吕 锋，王 虹，刘皓春，等.信息理论与编码[M].北京:人民邮电出版社,2004.

[11] 邱云飞,王 威,刘大有,等.基于方差的CHI特征选择方法[J].计算机应用研究,2012,29(4):1304-1306.

[12] JIANG X Y,JIN S.An improved mutual information-based feature selection algorithm for text classification[C]//5th international conference on intelligent human-machine systems and cybernetics.[s.l.]:IEEE,2013:126-129.

[13] DING X,TANG Y.Improved mutual information method for text feature selection[C]//8th international conference on computer science & education.[s.l.]:IEEE,2013:163-166.

[14] 熊志斌,刘 冬.朴素贝叶斯在文本分类中的应用[J].软件导刊,2013,12(2):49-51.

[15] 李荣陆.文本分类及其相关技术研究[D].上海：复旦大学,2005.