基于运动捕捉系统的多旋翼飞行器实时测姿算法
石 鹏,赖际舟,吕 品,包 胜
(南京航空航天大学自动化学院,南京 211106)
0 引言
旋翼飞行器具有体积小、质量小且能耗低的特点,能够较好地在室内无GPS(Global Positioning System)环境中完成搜索、环境监测和救援等任务[1],是目前无人机领域的研究热点之一。
运动捕捉系统(Motion Capture System,MCS)在室内指定的区域内可以完成对标记点的捕捉,从而得到标记点的高精度位置信息[2]。将特定光点固定在旋翼飞行器上,根据固定点的位置信息能够得到该飞行器的位置、速度和姿态信息。MCS是旋翼飞行器室内飞行的重要导航手段,可以为旋翼飞行器室内飞行提供高精度参考基准[3-6],近年来受到了广泛关注。目前,MCS测姿通常采用的三标记点方案对标记点的安装有较为严格的几何空间约束,要求利用3个标记点描述出机体系的两个正交轴来建立机体系,导致标记点安装误差会引起较大的测姿误差。对此,本文提出了一种MCS高精度五点测姿算法,该算法可以有效地减小标记点的安装误差给测姿精度带来的影响,测姿精度高,能够为旋翼飞行器室内动态飞行时的姿态测量提供实时参考基准。
1 MCS传统三点测姿算法缺陷分析
MCS传统三点测姿算法利用3个标记点安装成直角三角形,以直角边为坐标轴建立机体系,从空间几何角度出发,根据线与线或线与面的夹角关系求解姿态角。
如图1所示,3个标记点(黑色实心点)确定的平面(p0)为机体横截面,且3点构成直角三角形,两条直角边记为L1和L2,导航坐标系(n系)的Xn轴、Yn轴和Zn轴两两构成的平面分别记为p1、p2和p3。该算法中以L1为机体纵轴,由L1与p1的夹角求俯仰角,由L1在p1上的投影与p3的夹角求航向角,由p0的法向量与p3法向量的夹角求横滚角。
该算法不仅要求3个标记点满足直角三角形的安装约束,而且要求两条直角边(记为L1和L2)分别与真实机体系的X轴、Y轴方向一致;然而标记点的安装常由人工完成,难以保证安装精度。
因此,三点测姿算法在旋翼飞行器上应用时会存在以下不足:当标记点的安装存在误差时,L1与机体纵轴位置存在偏差,且p0与机体横截面不重合,从而导致从测姿原理上产生较大测姿误差。
2 MCS五点测姿算法设计与分析
针对MCS中三点测姿算法测姿误差受标记点安装误差影响大的问题,本文设计了一种五点测姿算法。本节将对五点测姿算法流程进行阐述,并且对两种测姿算法的测姿误差进行对比分析。
2.1 五点测姿算法设计
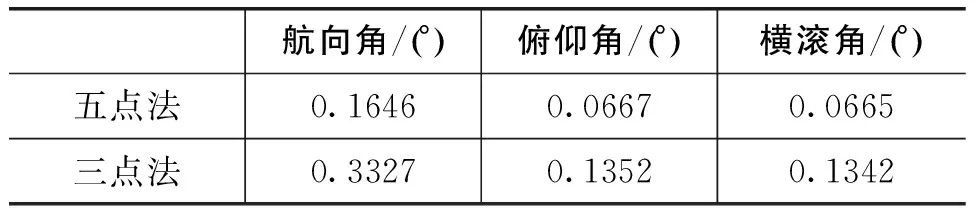
本文中的四旋翼飞行器测姿算法一共采用5个标记点安装在飞行器上,如图2所示。其中,A、B、C、D4点分别代表安装在机臂上的4个标记点,用来求解飞行器姿态。AB和CD中点的连线平行机头方向,第5个标记点G为辨识点,位于四边形ABCD内,用于辨识前4个标记点,其距离约束关系为AG 五点法标记点的安装没有角度约束要求,直接固定在四旋翼飞行器4个支架上,易于实现。采用旋转矢量法对载体姿态进行求解[7-9],其算法流程如图3所示,原理示意图如图4所示。 由于MCS下捕捉标记点得到的位置信息顺序是随机的,因此该算法中首先根据标记点的位置关系得到辨识点G信息,然后利用G与其他4点的距离关系辨识出A、B、C、D4点。 四旋翼飞行器的飞行动力由螺旋桨提供,通过A、B、C、D4点位置对旋翼所在位置进行全局平面拟合(S1),并由S1作为机体横截面建立机体坐标系,可以较好地与四旋翼飞行器的运动特性相对应[10],这是三点法所不具备的特点之一。 导航坐标系(n)为运动捕捉系统坐标系,Yn轴指向北,以拟合的平面S1为机体系的X-O-Y平面建立机体坐标系(b系)。本文中提到的机体系为右前上坐标系,记点H为AB中点,O点为四边形ABCD的中心。记O′、H′、A′和B′分别为O、H、A和B投影到平面S1的投影点,以O′点为b系原点Ob,O′点和A′B′中点(点H′)确定的射线为Yb轴。记ti、tj、tk分别为Xb轴、Yb轴、Zb轴上方向为正方向的单位向量,Yb轴对应机体的机头方向。则: (1) 根据向量O′A′和O′B′叉乘可以求得X-O-Y平面的法向量,作为Zb轴: (2) 由Yb轴和Zb轴的关系可以建立Xb轴: ti=tj×tk (3) (4) (5) 五点测姿算法和三点测姿算法的测姿精度取决于其建立的机体系的准确度,因此从两种测姿算法确定的机体系与真实机体系的偏差来分析测姿误差大小。 图5中,b0系为真实机体系。三点法中,由B、C、D3点确定机体系b1求姿态角,L1为Yb1轴,L2为Xb1轴;五点法中,由A、B、C、D4个标记点确定机体系b2求姿态角。 三点法中,理想情况为L1和L2分别平行于Yb0轴和Xb0轴。实际情况中,安装误差可以描述为:L1在Xb0轴和Zb0轴的投影长度为Δl1,L2在Yb0轴和Zb0轴的投影长度为Δl1。b0系绕Zb0反向转动Δψi,再绕Xb0正向转动Δθi,再绕Yb0正向转动Δγi得到bi系(i=1,2),有: (6) (7) (8) 通过拟合四旋翼所在平面和4个标记点确定Xb0轴方向的方法,五点法在确定机体系的过程中能够补偿部分标记点安装误差带来的误差。考虑到对比的直观性,在式(6)和式(7)中,五点法在三轴方向上的安装误差等价于Δl2(Δl2<Δl1)。 (9) (10) 由此看出,本文提出的五点测姿算法可以降低安装标记点的几何空间约束,并减小安装误差对测姿误差的影响,因此五点法的测姿误差比三点法小。 为验证提出的五点测姿法的测姿精度,将标记点安装在三轴小型机械转台的转台平面上,通过转台平面(相当于机体系X-O-Y平面)的变化模拟四旋翼飞行器姿态角变化。实验分为实验1和实验2,实验中同时改变转台转动的3个姿态角,将三点法与五点法的测姿结果与转台转动角度进行对比,并分析其均方根误差(RMSE)。实验1中,主要针对标记点的安装在与转台平面平行方向上存在误差时,对比两种算法的测姿精度。实验2相对于实验1,不仅考虑了标记点在与转台平面平行方向上的安装误差,还考虑了与转台平面的垂直方向上的安装误差。 实验1中,标记点直接粘贴在转台平面上,所有标记点共面,且其所在平面与转台平面平行。由表1和图6可知,将两种测姿算法结果与转台对比,其俯仰角和横滚角偏差相近,测姿精度相当;比较其航向角偏差,三点法大于五点法;比较其RMSE,五点法优于三点法。因此,当标记点安装误差主要存在于与转台平面平行方向上时,五点法优于三点法,主要体现于航向角的测量精度。 表1 实验1测姿均方根误差表 实验2中,给一个标记点(相对位置与图5中点C相同)在与转台平面的垂直方向上引入5mm的安装误差。由表2和图7可知,通过比较其姿态角偏差和RMSE得出结论,当标记点安装在转台系(机体系)三轴方向上都存在误差时,五点法的3个姿态角测量精度都明显优于三点法。 表2 实验2测姿均方根误差表 实验1和实验2的结果表明,针对实际应用时,标记点在机体系三轴方向上都存在安装误差,较三点测姿算法,五点测姿算法能够通过补偿标记点安装误差来减小测姿误差,其测姿RMSE值小于0.2°,保证了测姿精度,测姿效果更好。 此外,为进一步验证五点测姿法在多旋翼飞行器中的应用效果,进行了基于该方法的四旋翼飞行器航迹飞行实验。图8和图9为其飞行航迹图,图10为利用五点测姿算法对其实时动态测姿图。结果表明,应用五点测姿算法,能够较好地完成旋翼飞行器实时动态测姿任务。 本文提出的基于运动捕捉系统的多旋翼飞行器室内五点测姿算法相对于MCS中常用的三点测姿算法,减小了测姿误差,且易于实现。五点测姿算法利用四点位置对旋翼所在位置进行全局平面拟合,较好地与其结构特性相对应,并通过拟合平面建立机体系,能够有效地降低由标记点的安装误差产生的测姿误差。室内实验结果表明,本文提出的五点测姿算法的3个姿态角RMSE值均小于0.2°,较三点测姿算法,减小了标记点安装误差产生的测姿误差,实际应用时该算法测姿精度更高。四旋翼飞行器的航迹飞行实验结果表明,该算法能够有效实现四旋翼飞行器室内动态实时姿态测量,具有良好的工程应用价值。 [1]Weiss S, Scaramuzza D, Siegwart R. Monocular-SLAM-based navigation for autonomous micro helicopters in GPS-denied environments[J]. Journal of Field Robotics, 2011, 28(6): 854-874. [2]Park S W, Park H S, Kim J H, et al. 3D displacement measurement model for health monitoring of structures using a motion capture system[J].Measurement, 2015,59: 352-362. [3]邵慧. 无人机高精度目标定位技术研究[D]. 南京航空航天大学, 2014. SHAO Hui. Research on high precision target localization technology in UAV [D]. Nanjing University of Aeronautics and Astronautics, 2014. [4]Lupashin S, Hehn M, Mueller M W, et al. A platform for aerial robotics research and demonstration: the flying machine arena[J]. Mechatronics, 2014, 24(1): 41-54. [5]赵继.基于运动捕捉系统的四旋翼飞行器导航控制技术研究[D].南京航空航天大学,2015. ZHAO Ji. Research on navigation and control technology of quadrotor based on motion capture system [D]. Nanjing University of Aeronautics and Astronautics, 2015. [6]Michael N, Mellinger D, Lindsey Q, et al. The GRASP multiple micro-UAV testbed[J]. Robotics & Automation Magazine, IEEE, 2010, 17(3): 56-65. [7]Moutinho A, Figueira M, Azinheira J R. Attitude estimation in SO(3): a comparative UAV case study[J]. Journal of Intelligent & Robotic Systems, 2015, 80(3): 375-384. [8]Hua M D. Attitude estimation for accelerated vehicles using GPS/INS measurements[J]. Control Engineering Practice, 2010, 18(7):723-732. [9]Martin P, Salaün E. Generalized multiplicative extended Kalman filter for aided attitude and heading reference system[C]. AIAA Guidance, Navigation, & Control Conference, 2010. [10]Bernardini G, Serafini J, Colella M M, et al. Analysis of a structural-aerodynamic fully-coupled formulation for aeroelastic response of rotorcraft[J]. Aerospace Science & Technology, 2013, 29(1): 175-184.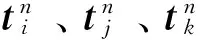

2.2 MCS两种测姿算法对比


3 算法验证

4 结论

