高烈度区近断层RC框架-核心筒高层结构隔震设计关键参数取值

李爱群　刘立德　曾德民　杨参天　解琳琳

(1北京建筑大学北京未来城市设计高精尖创新中心, 北京 100044)(2北京建筑大学土木与交通工程学院, 北京 100044)(3东南大学土木工程学院, 南京 210096)

近年来,功能可恢复已逐渐成为地震工程领域的研究热点．作为未来城市的一个重要组成部分,高层结构的地震功能可恢复日益得到诸多学者的广泛关注．对于处于高烈度近断层区域的RC框架-核心筒高层结构,由于设计时需对各地震水准的地震峰值加速度乘以一个不小于1.25的近场影响系数来放大地震作用[1],使得传统的抗震设计面临了极大的挑战,并且结构的抗震性能较难满足功能可恢复需求．理论上而言,隔震技术的引入可以有效降低上部结构的地震作用,在降低上部结构的设计难度的同时可以显著减小结构/非结构构件的损伤,有效提高该类高层结构的震后可恢复能力[2]．

无论是多层隔震结构还是高层隔震结构,其设计方法和设计流程存在一定的相似性．对于高烈度近断层区域的RC框架-核心筒高层结构,其设计需要明确:① 结构所承受的地震作用,在设防烈度和场地类别确定的前提下,地震作用仅取决于考虑近场效应的近场影响系数;② 结构的抗震能力,已有研究表明屈重比(隔震层铅芯支座总屈服力与上部结构重力比值[3-7])是决定隔震层力学性能、整体减震效果和结构抗震能力的重要参数．

对于屈重比这一关键设计参数,王曙光等[3]对某一外套加层隔震体系进行了研究,对于位于7度区的该类结构建议合理屈重比取值为2.5%～4%. 李冰[4]对8层混凝土结构进行研究,建议了该结构在7～9度设防时屈重比的合理取值. Providakis[5]和Mollaioli等[7]分别对不同屈重比下多层隔震结构的响应特征进行了研究,初步探索了屈重比对该类结构响应的影响．然而,上述研究多集中于多层结构屈重比的研究,目前对于高烈度近断层区RC框架-核心筒高层隔震结构屈重比的研究还相对较少．此外,结构高度和隔震设计方案对适用于该类结构的屈重比可能存在影响,相关研究还未见报道．

对于近场影响系数这一隔震结构关键设计参数,《建筑抗震设计规范》[1]对其做出了相关规定．杨迪雄等[8]和殷伟希等[9]研究了近断层RC隔震框架结构的地震响应特征,结果表明设计时应充分考虑近断层效应对于隔震结构的影响．韩淼等[10-12]系统研究了近断层地震动对2种典型多层隔震结构(包括层间隔震结构和基础隔震结构)动力响应的影响;刘文光等[13-14]基于1个典型钢框架-RC核心筒高层隔震结构,对比了高层隔震结构在近、远场地震动作用下的损伤特征,但并未考虑各影响因素的影响,也未针对近场影响系数的取值进行讨论．总的说来,综合考虑不同高度和隔震设计方案的影响,在合理的屈重比范围内揭示RC框架-核心筒高层隔震结构在近断层地震动作用下的响应特性以及近场影响系数取值的相关研究还相对较少.因此,本文以2栋设防烈度为8.5度、近断层且高度不同的RC框架-核心筒高层隔震工程案例为原型,考虑不同隔震设计方案(核心筒下沉隔震方案和±0隔震方案)的影响,基于精细有限元模型,研究了屈重比对该类结构减震系数和隔震层位移的影响规律,建议了适用于RC框架-核心筒高层隔震结构的合理屈重比取值范围．在此基础之上,本文综合考虑不同的结构高度、隔震设计方案和合理范围内的不同屈重比,研究了近断层RC框架-核心筒高层隔震结构的响应特征,初步探讨并建议了适用于该类结构的近场影响系数．

1　合理屈重比取值分析

1.1　原型结构简介

本研究选取了2栋(C1和C4)具有不同高度的RC框架-核心筒高层隔震工程案例作为原型结构,其抗震设防烈度均为8度(0.30g),场地类别为Ⅲ类场地,设计地震分组为第2组．2栋结构均近断层,专家委员会建议考虑近断层影响,相应的近场影响系数取为1.25．C1上部结构共22层79.2 m,地下4层16.05 m;C4上部结构共17层65.8 m,地下4层14.15 m．结构高宽比分别为2.30和1.91．核心筒剪力墙厚均为300～600 mm．结构三维示意图和平面布置图分别如图1和图2所示．

(a) C1

(b) C4

图1原型结构三维示意图

C1和C4的隔震层设置如图2所示．隔震层设置于地下室顶板和上部框架结构之间以及核心筒底部,相应的隔震支座主要参数如表1所示．为满足工程设计中对隔震层位移响应的要求(隔震沟宽度600 mm),上述结构在工程设计的过程中均采用了16个黏滞阻尼器．本研究团队设计了位于该场地的29栋不同的高层隔震结构,均采用16个阻尼器和相近的阻尼器参数,阻尼器的最大出力均在2 000 kN左右,因此在本研究中阻尼器不作为变量．C1和C4关键设计指标见表2．

(a) C1隔震方案

(b) C4隔震方案

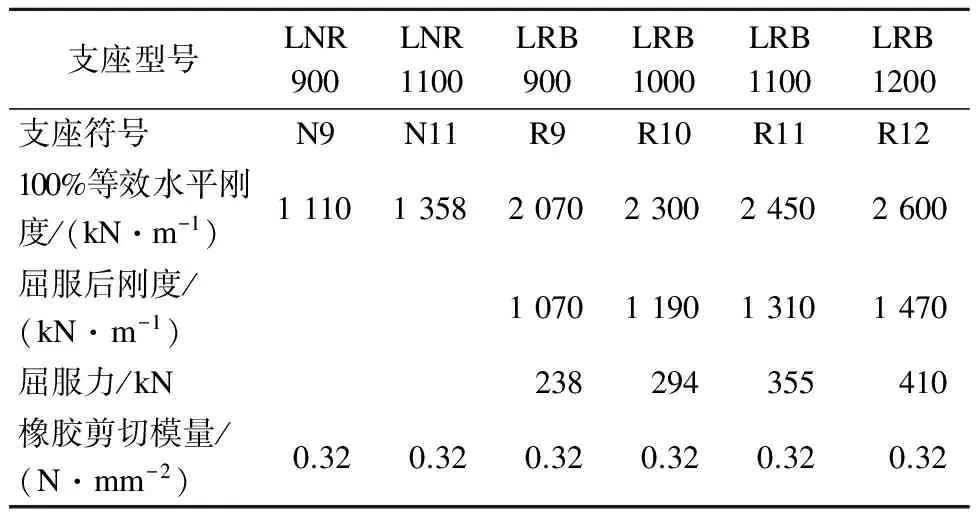
支座型号LNR900LNR1100LRB900LRB1000LRB1100LRB1200支座符号N9N11R9R10R11R12100%等效水平刚度/(kN·m-1)111013582070230024502600屈服后刚度/(kN·m-1)1070119013101470屈服力/kN238294355410橡胶剪切模量/(N·mm-2)0．320．320．320．320．320．32

1.2　案例设计

根据该类结构建筑使用功能的不同要求，选择不同的隔震设计方案．原型结构在设计过程中采用了局部地下室下沉隔震方案(核心筒部分下沉至地下室底部隔震,框架在整体±0处隔震),为了研究不同隔震设计方案的影响,本文采用了C1和C4的上部结构,设计了相应的整体±0隔震结构案例．

表2　结构参数及相应地震响应

为了研究合理屈重比取值,通过调整隔震支座的数量和位置来获得不同的屈重比,设计了一系列具有不同屈重比的高层隔震结构分析案例．通过对设计完成的29栋高层隔震结构中的10栋RC框架-核心筒高层隔震结构的屈重比统计分析可知,屈重比的变化范围为2.06%～3.43%．因此,本文屈重比上、下限值分别取为3.5%和1.5%,或尽量接近该值．28个案例的屈重比和相应周期如表3所示．

大震作用下隔震结构的上部结构损伤程度通常较轻,且该类结构的塑性行为主要集中在隔震层,因此采用单质点模型或弹性剪切层模型模拟上部结构,采用弹塑性模型模拟隔震层[15-16]．对于上部结构,本研究也采用弹性模型模拟[17-19],然而不同于多层框架结构,框架-核心筒呈现出明显的弯剪耦合特性[20],而传统的剪切层模型无法反映这一特性对结构响应的影响．因此,本文基于ETABS建立各隔震结构的精细模型,其中上部结构为弹性模型,隔震层为弹塑性模型．隔震支座采用Rubber Isolator单元与Gap单元模拟,黏滞阻尼器、梁柱和剪力墙分别采用Damper-Exponential单元、Frame单元和壳单元模拟．

表3　分析案例基本信息

本文采用了实际工程中使用的2条天然地震动和1条人工地震动,上述地震动的加速度反应谱与规范谱的对比如图3所示．从图中可以看出,在1.31～1.59 s(非隔震结构周期段)和3.90～4.95 s(隔震结构周期段)内各地震动加速度反应谱值与规范反应谱值最大误差不超过35%,平均误差不超过20%,满足规范要求,表明上述地震动可用于设计具有不同屈重比和不同隔震方案的RC框架-核心筒高层隔震结构．

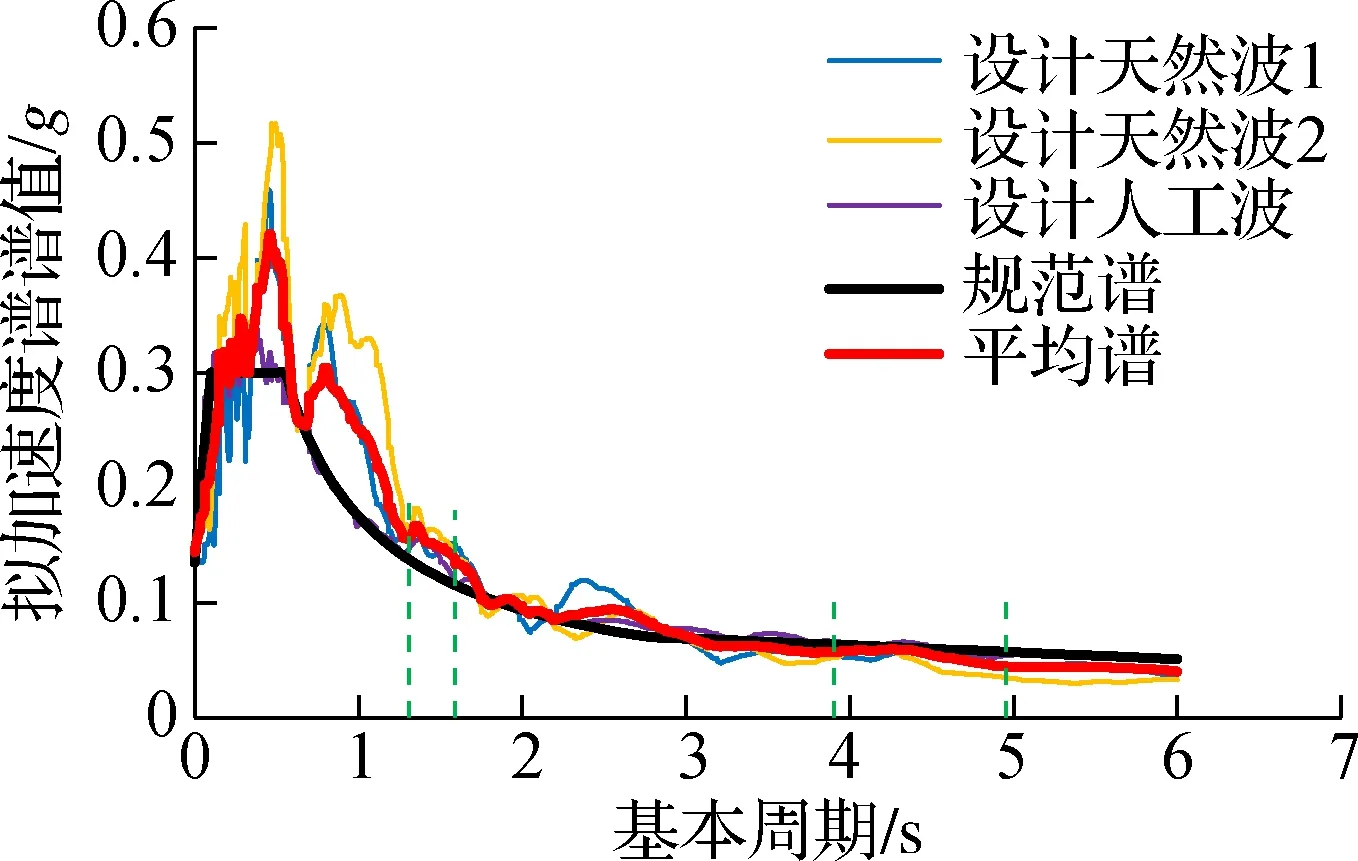
图3　设计地震动反应谱与规范反应谱对比

考虑近断层影响,采用3条设计地震动对上述28个高层隔震结构进行隔震设计．将上述地震动分别调幅至375和637.5 cm/s2，进行中震和大震下的动力时程分析．

1.3　合理屈重比取值

减震系数是评价隔震效率的重要指标,当隔震层设置了阻尼器时,减震系数不应超过0.38．隔震沟尺寸是影响结构使用功能的重要参数,在隔震设计中,需首先确定大震下1.15倍隔震层质心位移和角点位移的较大值,即大震隔震层位移(maximum bearing displacement, MBD),在此基础上乘以1.2的放大系数用于确定隔震沟尺寸．本研究考虑各栋结构的设计难度,将隔震沟的尺寸限值放宽至650 mm,即MBD放宽至540 mm．因此,本研究将以减震系数不超过0.38和MBD不超过540 mm作为控制指标,确定适用于RC框架-核心筒高层隔震结构的合理屈重比取值范围．

各案例的减震系数和MBD在3条地震动作用下的包络值如图4～图7所示．从图中可以看出,屈重比的取值对隔震结构关键响应(减震系数和MBD)具有显著的影响,即

1) 当屈重比不超过3%时,减震系数均不超过0.38,可满足规范要求,因此可将3%作为该类结构屈重比的上限值．整体来说,随着屈重比的减小减震系数有所减小,表明较小的屈重比可以获得更理想的减震效果．然而当屈重比减小至2%后,减震系数趋于一稳定值,这表明继续减小屈重比已无法获得更好的减震效果．此外,对于高度为65.8 m的C4结构,该上限值为3.5%,这表明随着结构高度的减小,屈重比上限值有增大的趋势．因此,对于高度小于80 m的RC框架-核心筒高层隔震结构,随着结构高度的减小可适当提高屈重比上限值．

(a) 减震系数

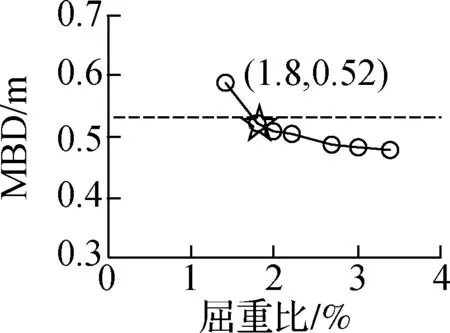
(b) 大震位移

图4C1,下沉隔震方案

(a) 减震系数

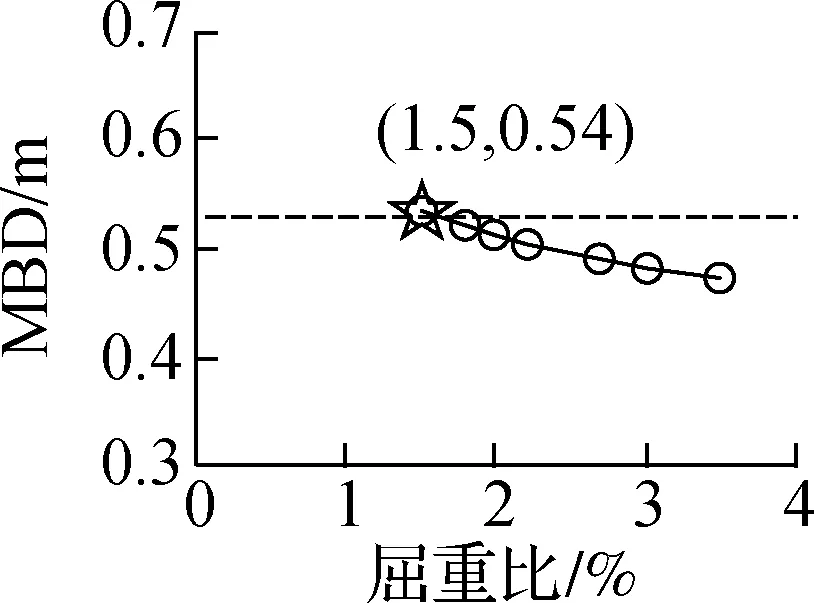
(b) 大震位移

图5C1,整体±0隔震方案

(a) 减震系数

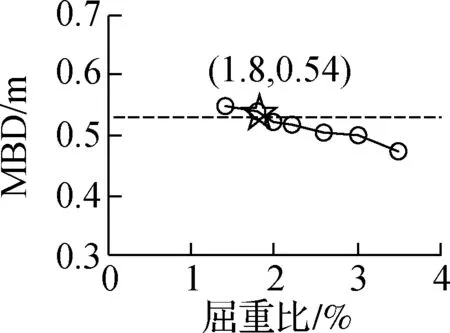
(b) 大震位移

图6C4,下沉隔震方案

(a) 减震系数

(b) 大震位移

图7C4,整体±0隔震方案

2) 当屈重比不小于2%时,大震隔震层最大位移MBD均不超过540 mm,可满足本研究预设的隔震沟尺寸要求,因此可将2%作为该类结构屈重比的下限值．整体来说,随着屈重比的增大，MBD有所减小,表明较大的屈重比可以更好地满足隔震沟的尺寸要求以及建筑使用功能要求．此外,对于高度为79.2 m的C1,该下限值最大为1.8%．当屈重比降低至2%后对于减震效率的提升相对不明显,而隔震层位移会有所增大,因此对于该类结构屈重比下限值均可取为2%．

综上所述,减震系数和隔震沟尺寸限值要求决定了RC框架-核心筒高层隔震结构屈重比的上限值和下限值,基于上述研究,对于高度不超过80 m的结构相应的屈重比的合理取值范围为2%～3%．

2　近场影响系数取值

2.1　基本案例及地震动选取

文献[13-14]基于个别案例研究了近断层地震动作用下高层框架-核心筒结构的响应特征．然而,综合考虑多种因素对该类结构在近场和远场地震动作用下的响应特征的研究还相对较少．近场影响系数的取值对该类结构的设计影响较大,1.25的取值能否较好反映近断层影响并保证结构的安全性有待进一步确认．

本文在获得了该类高层隔震结构的合理屈重比范围的基础上,选取了上文28个案例中的12个典型案例,考虑了:① 79.2 m(C1)和65.8 m(C4)2种结构高度;② 核心筒下沉隔震方案和±0隔震方案2种隔震设计方案;③ 2%,2.6%或接近2.6%和3%的不同屈重比．基于上述案例,研究近场和远场地震动下该类结构的响应特征，初步探索适用于该类结构的近场影响系数．

不同于隔震结构的分步设计,近场地震动作用下隔震结构的响应特征研究所关注的是结构整体的受力行为．因此本文在选取近场和远场地震动时根据隔震后的结构基本周期选取相应的地震动．为了考虑地震动的离散性,对于远场和近场地震动均选取了7条天然地震动．建筑抗震设计规范对于断层距在5 km以内的结构建议了更严格的近场影响系数,本文在选取近场地震动集时均将断层距限制在5 km内．基于上述原则,选取了7条近场和远场地震动,相应的地震动信息如表4所示,其加速度反应谱与规范谱对比如图8所示．

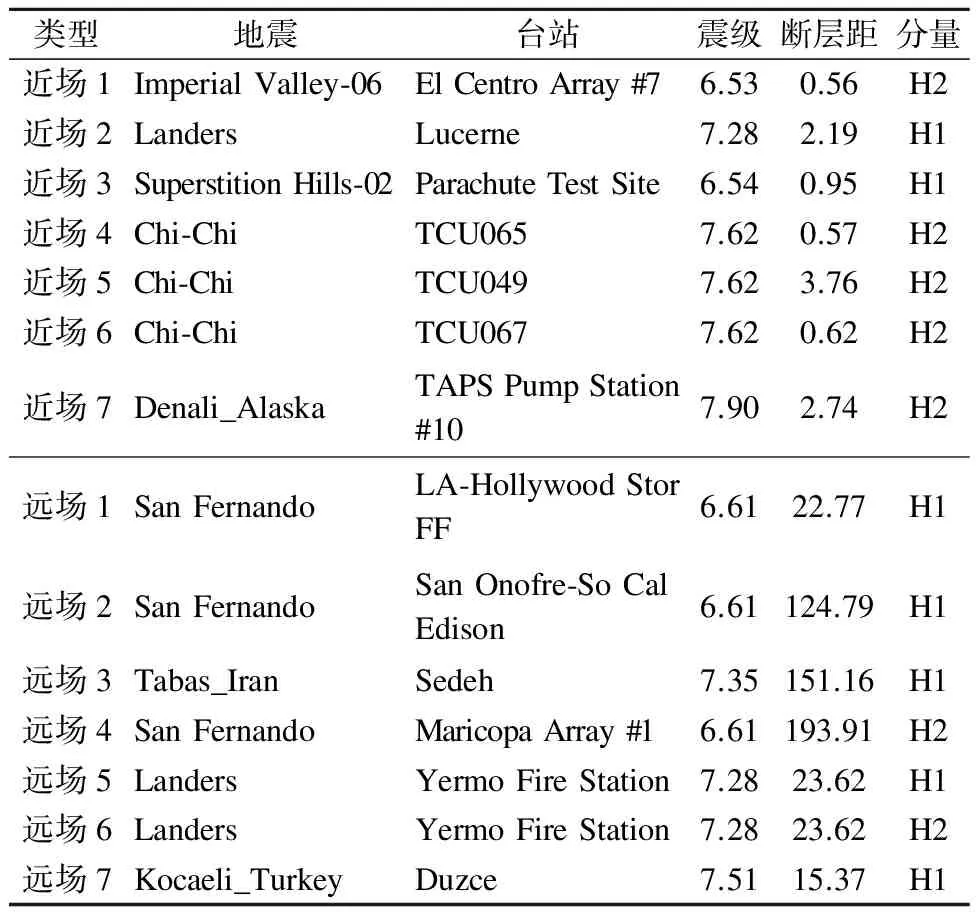
表4　选取的远场和近场地震动信息

(a) 远场地震动

(b) 近场地震动

图8选取的远场和近场地震动反应谱与规范反应谱对比

2.2　远场和近场地震动下结构响应特性

将上述14条天然地震动分别调幅至300和510 cm/s2,分别对应于结构的设计地震和罕遇地震峰值加速度,沿结构的一阶周期方向对上述12个模型进行输入,进行中震和大震下的动力时程分析,获取各结构在不同地震动作用下的中震楼层剪力包络分布、大震楼层层间侧移角包络分布、大震楼面加速度包络分布和最大隔震层位移．

不同结构在近场和远场地震动下的楼层响应分布呈现出相似的规律．本文以屈重比为2.7%的C1核心筒下沉结构设计案例为例,详细阐述远场和近场地震动作用下结构的响应特性．核心筒下沉隔震方案在远场和近场地震动作用下的响应如图9所示．对于2种不同的隔震设计方案,在近场和远场地震动作用下剪力、层间侧移角和楼面加速度的分布基本相似．楼面加速度呈现出明显的K形分布特征,这与传统的多层隔震结构的楼面加速度分布相近[8,21];近场地震动作用下的关键结构响应均显著大于远场地震动作用下的关键结构响应．

(a) 远场中震剪力

(b) 远场大震层间侧移角

(c) 远场大震楼面加速度

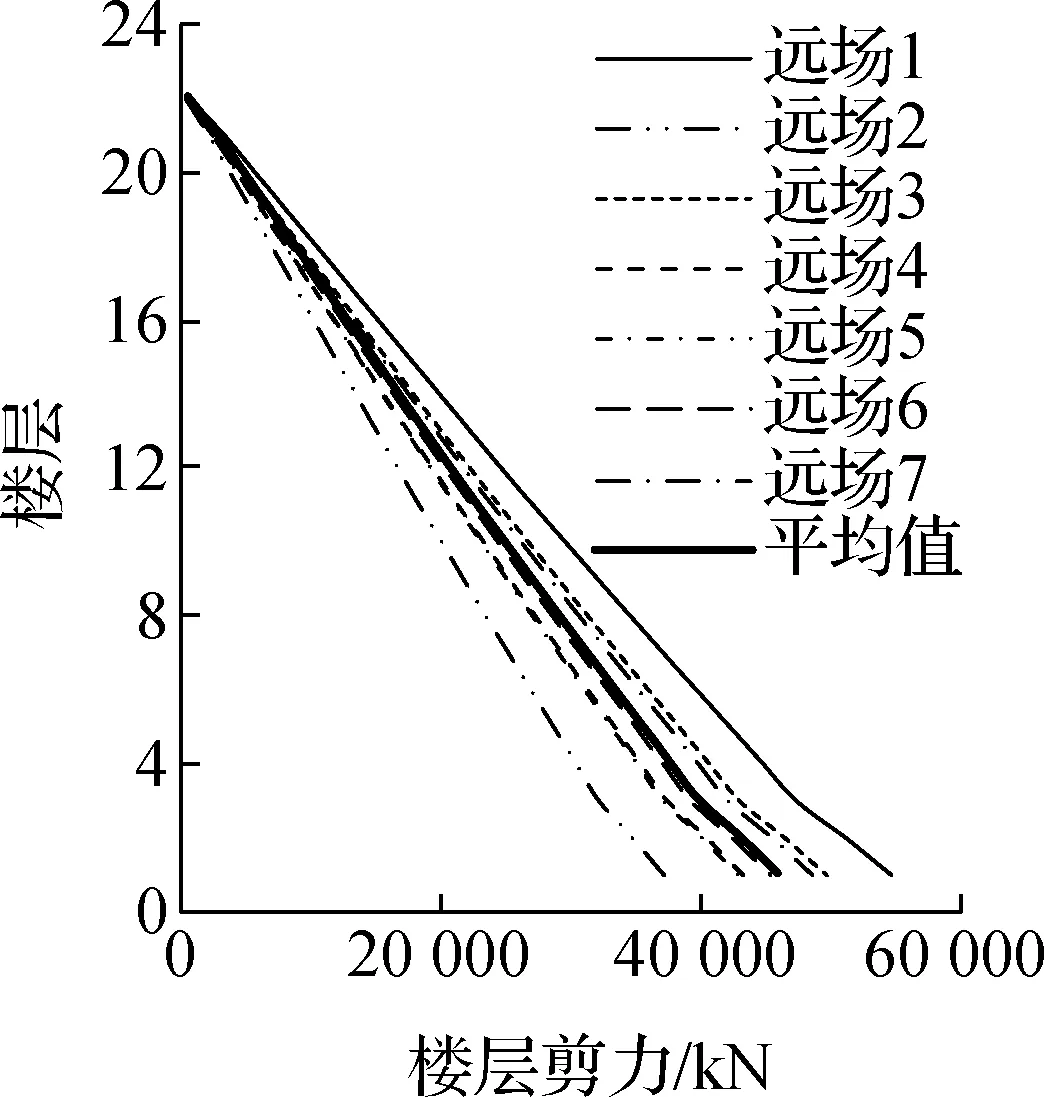
(d) 近场中震剪力

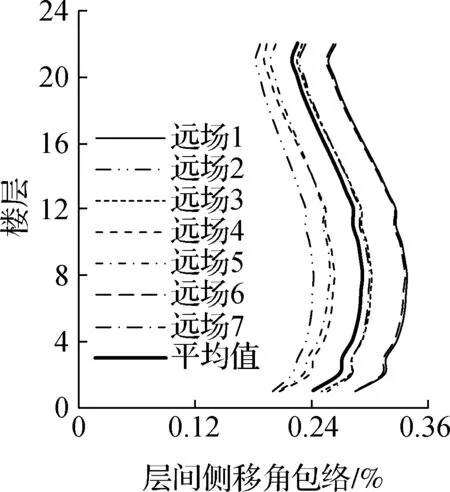
(e) 近场大震层间侧移角

(f) 近场大震楼面加速度

图9C1下沉隔震方案2.7%屈重比结构关键响应

为了进一步量化近场地震动作用下结构响应的放大效应,本文分别计算各案例结构在7条远场和近场地震动下的4种关键结构响应的平均值,包括结构中震基底剪力最大值(maximum base shear force, MBS)、大震最大层间侧移角(maximum inter-story drift ratio, MIDR)、大震最大楼面加速度(maximum floor acceleration, MFA)和大震最大隔震层位移(MBD)．相应的结果对比如表5～表8所示．从表中可以看出,近场地震作用下结构的MBS,MIDR,MFA和MBD分别是远场地震下的1.10～1.12倍、1.09～1.19倍、1.08～1.21倍和1.26～1.42倍．

表5　各隔震案例远场和近场地震动作用下中震基底剪力最大值(MBS)　kN

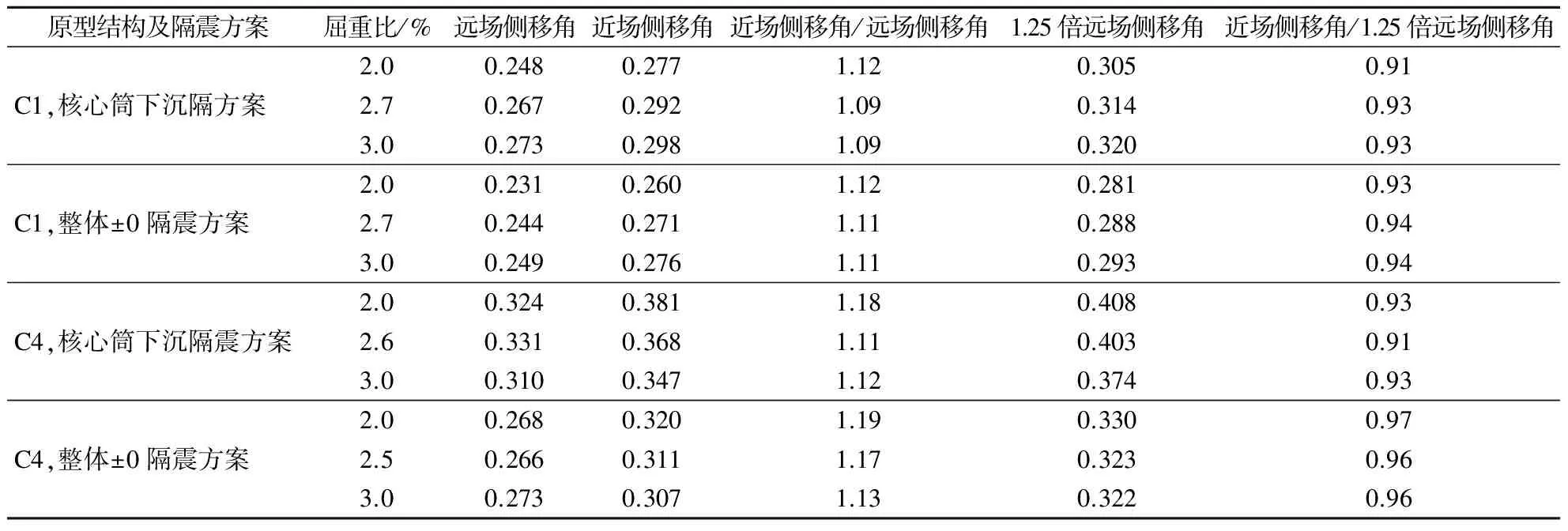
表6　隔震各案例远场和近场地震动作用下大震最大层间侧移角(MIDR)　%

表7　隔震各案例远场和近场地震动作用下大震最大楼面加速度(MFA)　m/s2

表8　隔震各案例远场和近场地震动作用下大震最大隔震层位移(MBD)　mm

2.3　近场影响系数取值分析

由上节分析可知,对于RC框架-核心筒高层结构,近场和远场地震作用下隔震层位移的比值介于1.26～1.42之间,其他响应的比值介于1.1～1.2之间．在设计时如何选取合适的近场影响系数,提升设计地震峰值加速度以考虑近场放大效应成为该类结构设计中的关键问题．

为了明确1.25的近场影响系数对近断层效应且保证结构的地震安全性,本研究对上述12个案例结构进行7条远场地震动下考虑近场效应的动力时程分析,即将相应的中震峰值加速度和大震加速度分别调幅至375和637.5 cm/s2．若其平均响应最大值均大于未调幅近场地震动下的相应值,则表明1.25的近场影响系数可较好地反映近场效应影响并基本保证结构安全．

7条远场地震动作用下各分析案例结构的关键结构响应(MBS,MIDR,MFA和MBD)最大值的平均值如表5～表8所示．从表中可以看出,近场地震作用下结构的MBS,MIDR,MFA和MBD分别是1.25倍远场地震下的0.95～0.96倍、0.91～0.97倍、0.96～1.03倍和0.85～0.98倍．近场地震动作用下结构的关键响应均小于采用1.25作为近场影响系数放大后的远场地震动下的相应响应,仅楼面最大加速度超出了3%,可以忽略不计．这表明对于近断层的RC框架-核心筒高层隔震结构,在本文建议的屈重比范围内,近场影响系数可适当放宽至1.25．

3　结论

1) 减震系数和隔震沟尺寸要求分别决定了该类隔震结构屈重比的上限值和下限值,对于高度不超过80 m的结构,屈重比的合理取值范围为2%～3%．

2) 近场和远场地震动作用下的结构响应分布特征一致,但近场下的结构响应明显强于远场下的结构响应．近场地震作用下结构的大震最大隔震层位移是远场地震下的1.26～1.42倍,结构的中震基底剪力最大值、大震最大层间侧移角和大震最大楼面加速度是远场地震下的1.1～1.2倍左右．

3) 对于高度小于80 m的RC框架-核心筒高层隔震结构,即使采用不同隔震设计方案,在本文建议的合理屈重比范围内,当断层距小于5 km时,近场影响系数可适当放宽至1.25．

本文的相关研究成果可为近断层RC框架-核心筒高层结构隔震设计中的关键参数(屈重比和近场影响系数)取值提供参考,可为该类结构隔震设计方法的完善提供支撑．

参考文献(References)

[1] 中国建筑科学研究院. GB 50011—2010 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2016.

[2] Stephen Mahin. 近期地震教训:建立更多可恢复性城市[J]. 建筑结构, 2012, 42(s1): 1-8.

Stephen Mahin. Lessons from recent earthquakes: The need for more resilient cities[J].BuildingStructure, 2012,42(s1): 1-8. (in Chinese)

[3] 王曙光, 赵学斐, 苗启松，等. 加层隔震结构隔震支座参数优化及试验研究[J]. 振动工程学报, 2013, 26(5): 722-731. DOI:10.3969/j.issn.1004-4523.2013.05.011.

Wang Shuguang, Zhao Xuefei, Miao Qisong, et al. Parameter optimization of isolator in structure with added floors and related shaking table tests[J].JournalofVibrationEngineering, 2013,26(5): 722-731. DOI:10.3969/j.issn.1004-4523.2013.05.011. (in Chinese)

[4] 李冰. 基于Benchmark模型的隔震层相关参数和地震反应计算分析与研究[D]. 广州: 广州大学土木工程学院, 2013.

[5] Providakis C P. Effect of LRB isolators and supplemental viscous dampers on seismic isolated buildings under near-fault excitations[J].EngineeringStructures, 2008,30(5): 1187-1198. DOI:10.1016/j.engstruct.2007.07.020.

[6] Avsar Ö, Özdemir G. Response of seismic isolated bridges in relation to intensity measures of ordinary and pulse-like ground motions[J].JournalofBridgeEngineering, 2013,18(3): 250-260. DOI:10.1061/(asce)be.1943-5592.0000340.

[7] Mollaioli F, Lucchini A, Cheng Y, et al. Intensity measures for the seismic response prediction of base-isolated buildings[J].BulletinofEarthquakeEngineering, 2013,11(5): 1841-1866. DOI:10.1007/s105 18-013-9431-x.

[8] 杨迪雄, 李刚, 程耿东. 近断层脉冲型地震动作用下隔震结构地震反应分析[J]. 地震工程与工程振动, 2005, 25(2): 119-124. DOI:10.3969/j.issn.1000-1301.2005.02.021.

Yang Dixiong, Li Gang, Cheng Gengdong. Seismic analysis of base-isolated structures subjected to near-fault pulse-like ground motions[J].EarthquakeEngineeringandEngineeringDynamics, 2005,25(2): 119-124. DOI:10.3969/j.issn.1000-1301.2005.02.021. (in Chinese)

[9] 殷伟希, 李云华. 近场地震动对基础隔震结构的影响[J]. 广东土木与建筑, 2009, 16(10): 16-18.

Yin Weixi, Li Yunhua. Research on isolated structures on near-field ground motions[J].GuangdongArchitectureCivilEngineering, 2009,16(10): 16-18. (in Chinese)

[10] 韩淼, 绳雯, 温增平. 近场橡胶支座隔震设计探讨[J]. 工程抗震与加固改造, 2013, 35(4): 104-108,123. DOI:10.3969/j.issn.1002-8412.2013.04.017

Han Miao, Sheng Wen, Wen Zengping. Discuss of rubber bearing isolation design on near-fault ground motions[J].EarthquakeResistantEngineeringandRetrofitting, 2013,35(4): 104-108,123. DOI:10.3969/j.issn.1002-8412.2013.04.017. (in Chinese)

[11] 韩淼, 张文会, 朱爱东. 近断层地震动对层间隔震结构动力响应影响分析[J]. 世界地震工程, 2015, 31(2): 1-7．

Han Miao, Zhang Wenhui, Zhu Aidong. Analysis of near-fault ground motions influence on dynamic responses of inter-story isolation structures[J].WorldEarthquakeEngineering, 2015,31(2): 1-7. (in Chinese)

[12] 韩淼, 张文会, 朱爱东，等. 不同层隔震结构在近断层地震作用下动力响应分析[J]. 振动与冲击, 2016, 35(5): 120-124. DOI:10.13465/j.cnki.jvs.2016.05.019.

Han Miao, Zhang Wenhui, Zhu Aidong, et al. Dynamic response analysis for multi-story structures with different isolation stories under near-fault ground motions[J].JournalofVibrationandShock, 2016,35(5): 120-124. DOI:10.13465/j.cnki.jvs.2016.05.019. (in Chinese)

[13] 刘文光, 刘阳, 何文福，等. 隔震结构动力弹塑性分析地震记录选择的波谱分类法研究[J]. 建筑结构学报, 2015, 36(7): 106-114. DOI:10.14006/j.jzjgxb.2015.07.014

Liu Wenguang, Liu Yang, He Wenfu, et al. Wave spectrum classification method of seismic records selection for isolated structure dynamic elasto-plastic analysis[J].JournalofBuildingStructures, 2015,36(7): 106-114. DOI:10.14006/j.jzjgxb.2015.07.014. (in Chinese)

[14] 刘阳. 高层隔震结构地震响应及损伤评估研究[D]. 上海: 上海大学土木工程系, 2014.

[15] 耿方方, 丁幼亮, 谢辉，等. 近断层地震动作用下长周期结构的地震动强度指标[J]. 东南大学学报(自然科学版), 2013, 43(1): 203-208. DOI:10.3969/j.issn.1001-0505.2013.01.037

Geng Fangfang, Ding Youliang, Xie Hui, et al. Ground motion intensity indices or long period structures subjected to near-fault ground motion[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2013,43(1): 203-208. DOI:10.3969/j.issn.1001-0505.2013.01.037. (in Chinese)

[16] 王维, 李爱群. 最小地震剪力系数对隔震结构抗震性能的影响[J]. 建筑结构学报, 2017, 38(1): 99-105. DOI:10.14006/j.jzjgxb.2017.01.011.

Wang Wei, Li Aiqun. Influence of minimum earthquake shear force coefficient on seismic performance of isolation structures[J].JournalofBuildingStructures, 2017,38(1): 99-105. DOI:10.14006/j.jzjgxb.2017.01.011. (in Chinese)

[17] 刘文光, 杨巧荣, 周福霖. 大高宽比隔震结构地震反应的实用分析方法[J]. 地震工程与工程振动, 2004, 24(4): 115-121. DOI:10.3969/j.issn.1000-1301.2004.04.021

Liu Wenguang, Yang Qiaorong, Zhou Fulin. Simplified method of earthquake response analysis for slender isolated structure[J].EarthquakeEngineeringandEngineeringDynamics, 2004,24(4): 115-121. DOI:10.3969/j.issn.1000-1301.2004.04.021. (in Chinese)

[18] 冯启浩, 周云, 卢德辉. 隔震支座拉压刚度比对高层隔震结构抗倾覆性能影响研究[J]. 工程抗震与加固改造, 2016, 38(1):52-59. DOI:10.16226/j.issn.1002-8412.2016.01.008.

Feng Qihao, Zhou Yun, Lu Huide. Influence on antidumping performance by NCOGAS and different rubber bearing tensile and compression stiffness ratios[J].EarthquakeResistantEngineeringandRetrofitting, 2016,38(1): 52-59. DOI:10.16226/j.issn.1002-8412.2016.01.008. (in Chinese)

[19] 翁大根, 刘帅, 李霄龙，等. 软土地基结构隔震方案及其工程应用[J]. 建筑结构学报, 2015, 36(2):41-50. DOI:10.14006/j.jzjgxb.2015.02.006.

Weng Dagen, Liu Shuai, Li Xiaolong, et al. Research and application of structural seismic isolation in soft ground[J].JournalofBuildingStructures, 2015,36(2):41-50. DOI:10.14006/j.jzjgxb.2015.02.006. (in Chinese)

[20] 熊琛, 许镇, 陆新征，等. 适用于城市高层建筑群的震害预测模型研究[J]. 工程力学, 2016, 33(11): 49-58. DOI:10.6052/j.issn.1000-4750.2015.08.0713.

Xiong Chen, Xu Zhen, Lu Xinzheng, et al. A urban seismic damage analysis model for tall building groups[J].EngineeringMechanics, 2016,33(11): 49-58. DOI:10.6052/j.issn.1000-4750.2015.08.0713. (in Chinese)

[21] 日本建筑学会. 隔震结构设计[M]. 刘文光，译. 北京: 地震出版社, 2006.