损伤可控摇摆墙滞回性能分析

崔浩然　 吴　刚　 冯德成　 张　简　 许嘉辉

(东南大学混凝土及预应力混凝土结构教育部重点实验室,南京210096)

1960年智利地震中的高位水槽结构因基础抬升而免遭破坏,Housner[1]对此提出了一个简化摇摆模型.此后,各国学者开始研究不同的摇摆结构,周颖等[2]对已有的摇摆自复位结构进行了总结.摇摆结构可在变形集中的界面设置阻尼器.Eatherton等[3]提出了可更换的耗能装置.Gu等[4]将2片木墙体中间附加U型耗能阻尼器.胡晓斌等[5]分析了预应力和底部耗能阻尼器对摇摆墙体滞回性能的影响.钢筋混凝土构件在摇摆运动后角部会破坏剥落,Roh等[6-9]研究了摇摆柱角部的退化和影响.Preti等[10]用高性能纤维增强混凝土修补摇摆墙的损伤角部.吕西林等[11]提出可恢复功能结构的概念,并在剪力墙脚部安装可更换的拉压组合减震支座.郝建兵[12]则提出了一种损伤可控结构.

本文提出了一种新型内嵌损伤可控摇摆墙.将摇摆体简化为刚体,推导出损伤可控摇摆墙的恢复力关系,并对滞回性能进行了参数化分析.

1　损伤可控摇摆墙的特点

框架结构内的损伤可控摇摆墙布置如图1(a)所示.每套损伤可控摇摆墙将2片刚性摇摆体通过可更换剪切阻尼器连接,后张无黏结预应力筋,穿过摇摆体中心,锚固于相同的下连接梁和上连接梁.每个摇摆体的角部单元为高延性弹性材料.计算模型如图1(b)所示.图中,H为摇摆刚体高度;L为刚体接触面宽度;a,b分别为角部宽度和高度;D1,D2分别为上、下连接梁高度;s为摇摆体轴线距离;t为摇摆体边距;LP为预应力筋长.

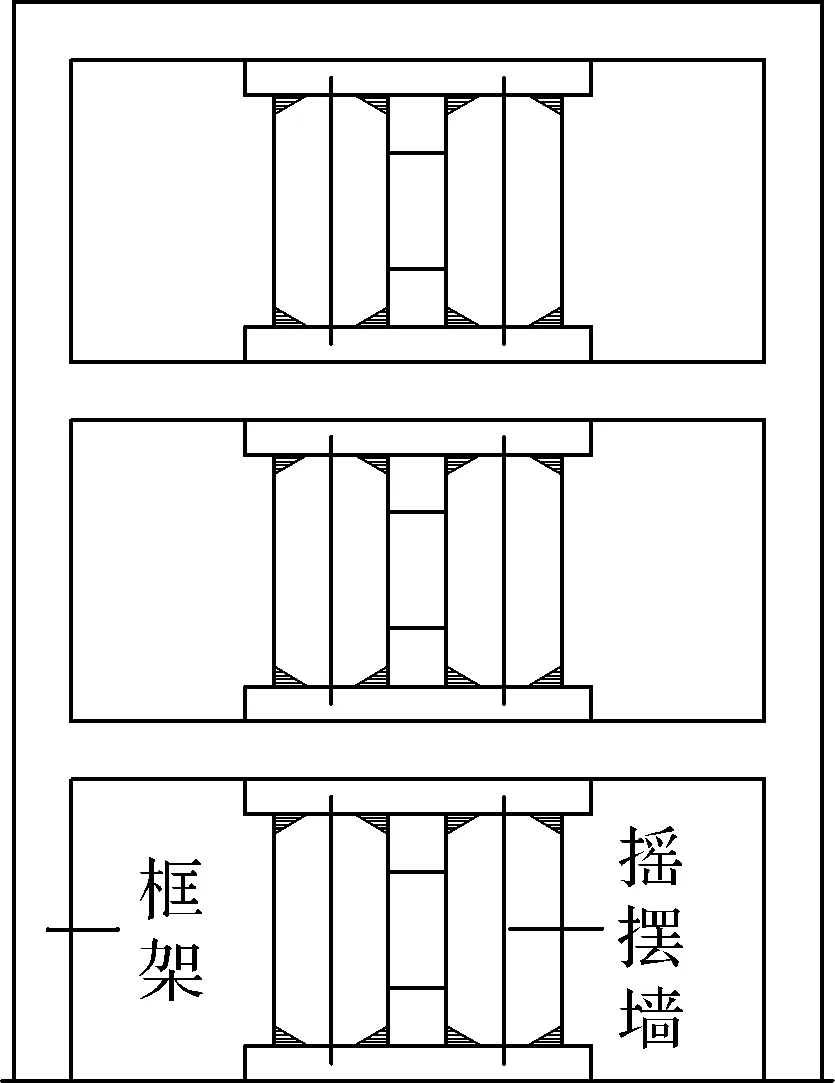
(a) 框架内嵌摇摆墙

1.1　预应力筋锚固位置

(1)

顶部施加的水平推力为

(2)

式中,P0,SP,E分别为预应力筋的初始预应力、面积和弹性模量.

(a) 新型摇摆墙

(b) 传统摇摆墙

图2不同摇摆墙示意图

(a) 新型摇摆墙

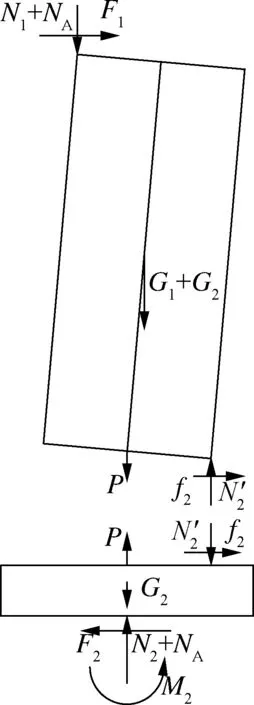
(b) 传统摇摆墙

图3不同摇摆墙受力分析

对于图2(b)所示的传统预应力自复位摇摆墙,后张无黏结预应力筋两端分别锚固于基础和墙体顶部.假定各参数均与新型摇摆墙相同,转动时受力如图 3(b)所示.当转动角为θ时,预应力筋长度增量为Lsin(θ/2),相应的预应力为

(3)

顶部施加的水平推力为

(4)

摇摆体转动相同角度时,本文提出的预应力筋锚固位置使新型摇摆墙预应力增量为传统摇摆墙预应力增量的2倍,预应力对新型摇摆墙恢复力的贡献超过对传统摇摆墙贡献的2倍.因此,摇摆墙内的预应力筋可采用本文提出的锚固位置,以提高预应力利用效率.

1.2　摇摆构件转动时的竖向位移

结构内部竖向摇摆构件在摇摆时产生的竖向位移可能会对主体结构产生不利作用.当矩形刚体以角部为中心的转动角θ较小时,竖向位移h与水平位移l的比值近似为墙体宽高比kα,即

(5)

相同水平位移下,摇摆体宽高比越大,竖向位移越大,实际中摇摆支撑点越容易因约束反力过大而损伤.因此,可将摇摆体的4个角部使用高延性材料(如聚氨酯橡胶弹性体或钢板橡胶叠合材料等),使摇摆体的转动点内缩,减小转动刚体的宽高比.支撑点由线接触变为面接触,减小应力集中并避免损伤,使摇摆墙性能稳定.

2　损伤可控摇摆墙恢复力关系

2.1　单调加载曲线

本文中剪切型耗能阻尼器为理想弹塑性,其刚度为KT,屈服力为Ty,计算模型见图1(b).假设在摇摆运动中2个摇摆体与上、下连接梁无相对滑动,忽略剪切阻尼轴压力.如图4所示,当摇摆体转动角为θ时,令l为摇摆墙顶部水平位移,h为顶部竖向位移,t′为摇摆体边距,ΔHt为2个摇摆体相邻边之间的错动距离.上述变量的计算公式分别为

l=Hsinθ+L(1-cosθ)

(6)

h=Lsinθ-H(1-cosθ)

(7)

t′=scosθ-L-2a

(8)

ΔHt=ssinθ

(9)

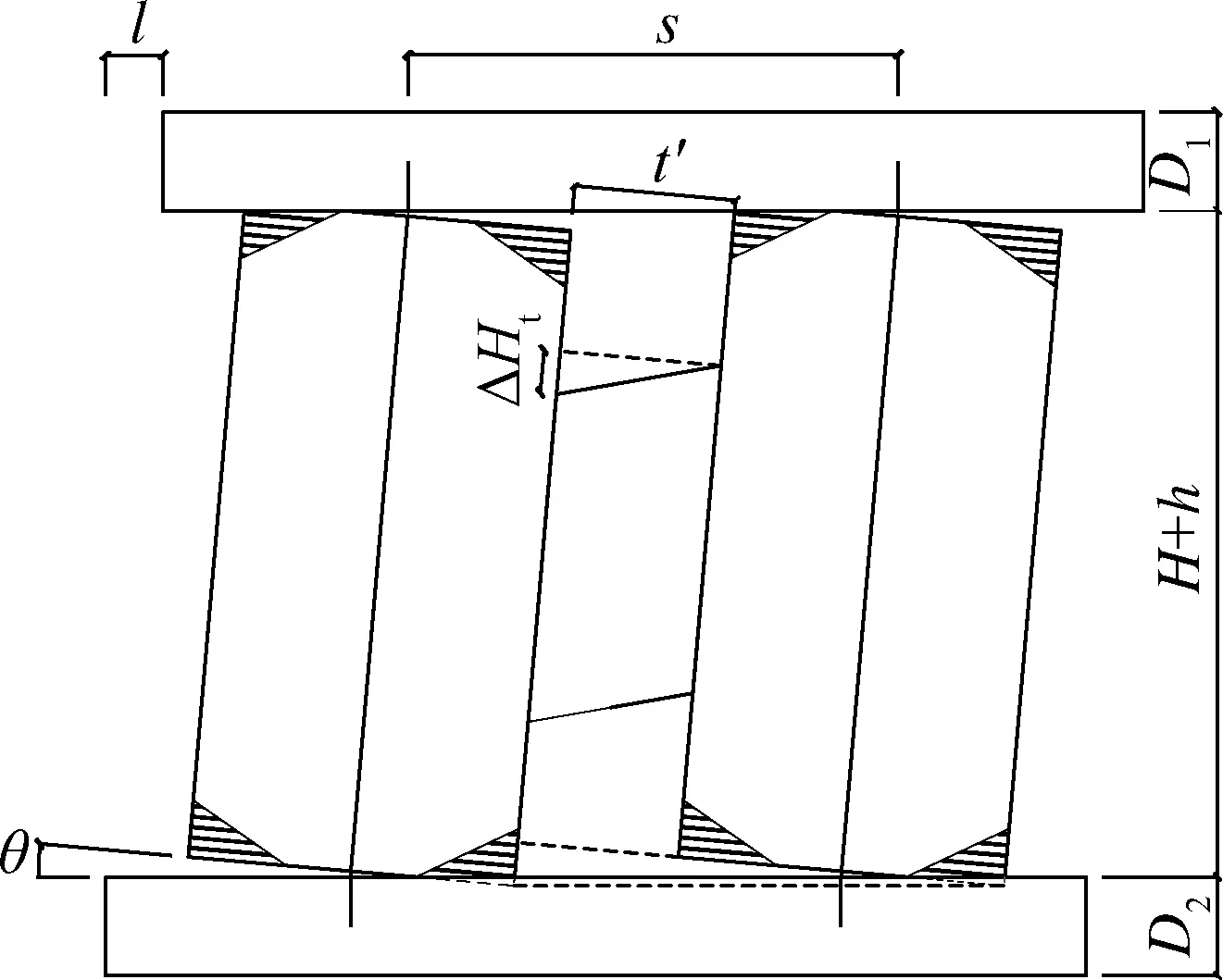
图4　损伤可控摇摆墙运动状态

损伤可控摇摆墙的受力分析如图5所示.假定角部理想弹性体接触面上的合力NM作用点位于接触面中心,则4个隔离体可建立12个独立的平衡方程,即

(10)

(11)

(12)

(13)

图5　损伤可控摇摆墙受力分析

(14)

(15)

(16)

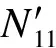
(17)

f11+Tsinθ=f12

(18)

(19)

(20)

f21=f22+Tsinθ

(21)

由方程组的特殊性可求得

(22)

式中

(23)

NA=KAh

(24)

NM=KMθ

(25)

(26)

式中,KA为摇摆体升高单位高度时主体结构对其轴向的反力;KM为摇摆体旋转单位角度时角部接触面的正应力合力.

图6为损伤可控摇摆墙的F-θ加载曲线.图中,点A为摇摆启动点,点B为阻尼屈服点,点C为卸载起始点.对于简化刚体模型,当预应力筋达到极限应力时,摇摆墙达到承载力极限,在此之前摇摆墙的承载力随位移增加.

图6　损伤可控摇摆墙的F-θ加载曲线

2.2　滞回性能

使用刚体简化模型分析的损伤可控摇摆墙的加载路径可由式(22)求得,卸载路径则与加载结束时的位置θr有关.对于简化模型,摇摆体为刚体,角部材料为弹性体,剪切阻尼为理想弹塑性,摇摆墙卸载到角度θ与加载到角度θ时仅剪切阻尼状态不同.因此,卸载时的水平恢复力计算公式也与式(22)相同,仅将阻尼力计算式改写为

(27)

如图7所示,当加载结束位置在点B时,θr=arcsin(Ty/(sKT)),加载卸载路径为O—A—B—A—O.当加载结束位置为点C1时,θr=2arcsin(Ty/(sKT)),加载卸载路径为O—A—B—C1—R1—Q1—O,其中阻尼力T在点B处屈服,阻尼力方向在点R1处反转,并在点Q1处反向屈服.当加载结束位置在点C2时,θr>2arcsin(Ty/(sKT)),加载卸载路径为O—A—B—C2—R2—Q2—Q1—O,其中阻尼力T在点B处屈服,阻尼力方向在点R2处反转,并在点Q2处反向屈服.滞回曲线O—A—B—C2—Q2—Q1—O包络的面积近似为

(28)

图7　损伤可控摇摆墙的滞回曲线

2.3　自复位条件

实现损伤可控摇摆墙刚体简化模型自复位后无残余变形,需满足图7中的点Q1在原点上方,即

(29)

实际工程中,考虑到钢筋混凝土的开裂屈服和墙体滑移等因素,应考虑一个大于1的安全系数Ks,即

(30)

2.4　抗滑移分析

2.1节推导中假设2个摇摆体和上、下连接梁在摇摆过程中无相对滑动,实际中的接触则会受到摩擦系数μ的影响.当需要的力大于静摩擦力极限时,摇摆体出现滑动,因此需满足

(31)

为防止摇摆体在摇摆运动过程中出现滑移,应在构造上采取保护措施,例如在墙体内部增设抗滑移钢棒[13].

3　滞回性能参数化分析

为研究剪切阻尼、角部块体、预应力筋等因素对损伤可控摇摆墙滞回性能的影响,将标准损伤可控摇摆墙各参数设置如下:G1=6.0 kN,G1=2.6 kN,N1=0,D=0.3 m,H=2 m,L=0.4 m,a=0.2 m,LP=2.3 m,t=0.3 m,SP=366 mm2,E=195 GPa,P0=250 kN,KA=0,KT=100 kN/mm,Ty=100 kN,KM=6 000 kN/rad.该摇摆墙简化模型的滞回性能在摇摆体达到极限位移角0.034 7 rad之前相似,假定卸载时摇摆体的转角θr=0.01 rad.

不同阻尼器屈服力Ty下摇摆墙的滞回曲线见图8.由图可知,增大阻尼屈服力时摇摆墙的摇摆起始点不变,墙体刚度不变,加载时屈服点的力和位移变大,卸载时反向屈服点的力和位移变小,与坐标轴纵轴的交点下移,当阻尼屈服力不满足式(29)时,墙体将产生残余位移.与标准墙比较,Ty增大50%时摇摆墙滞回曲线包围的面积增大40.5%;Ty减小50%时墙体滞回曲线包围的面积减小46.8%.

图8　不同阻尼屈服力下的摇摆墙滞回曲线

不同阻尼器刚度KT下摇摆墙的滞回曲线见图9.由图可知,增大阻尼刚度时摇摆墙的摇摆起始点不变,阻尼屈服后的所有滞回曲线相同,与坐标轴纵轴的交点不变.与标准墙比较,当KT增大100%时摇摆墙滞回曲线包围的面积增大6.5%,屈服前刚度增大90.8%;刚度KT减小50%时墙体滞回曲线包围的面积减小12.8%,屈服前刚度减小45.4%.

图9　不同阻尼刚度下的摇摆墙滞回曲线

不同角部刚度KM下摇摆墙的滞回曲线见图10.由图可知,增大角部刚度时摇摆墙的摇摆起始点不变,卸载时与坐标轴纵轴的交点不变,摇摆墙滞回曲线包围的面积不变.与标准墙相比,当KM增大50%时摇摆墙的屈服前刚度增大0.9%,屈服后刚度增大9.8%;KM减小50%时摇摆墙的屈服前刚度减小0.9%,屈服后刚度减小9.8%.同时,增大角部刚度,摇摆体转动相同角度时角部弹性体位置的分布力增大,摇摆体支撑点的力减小.

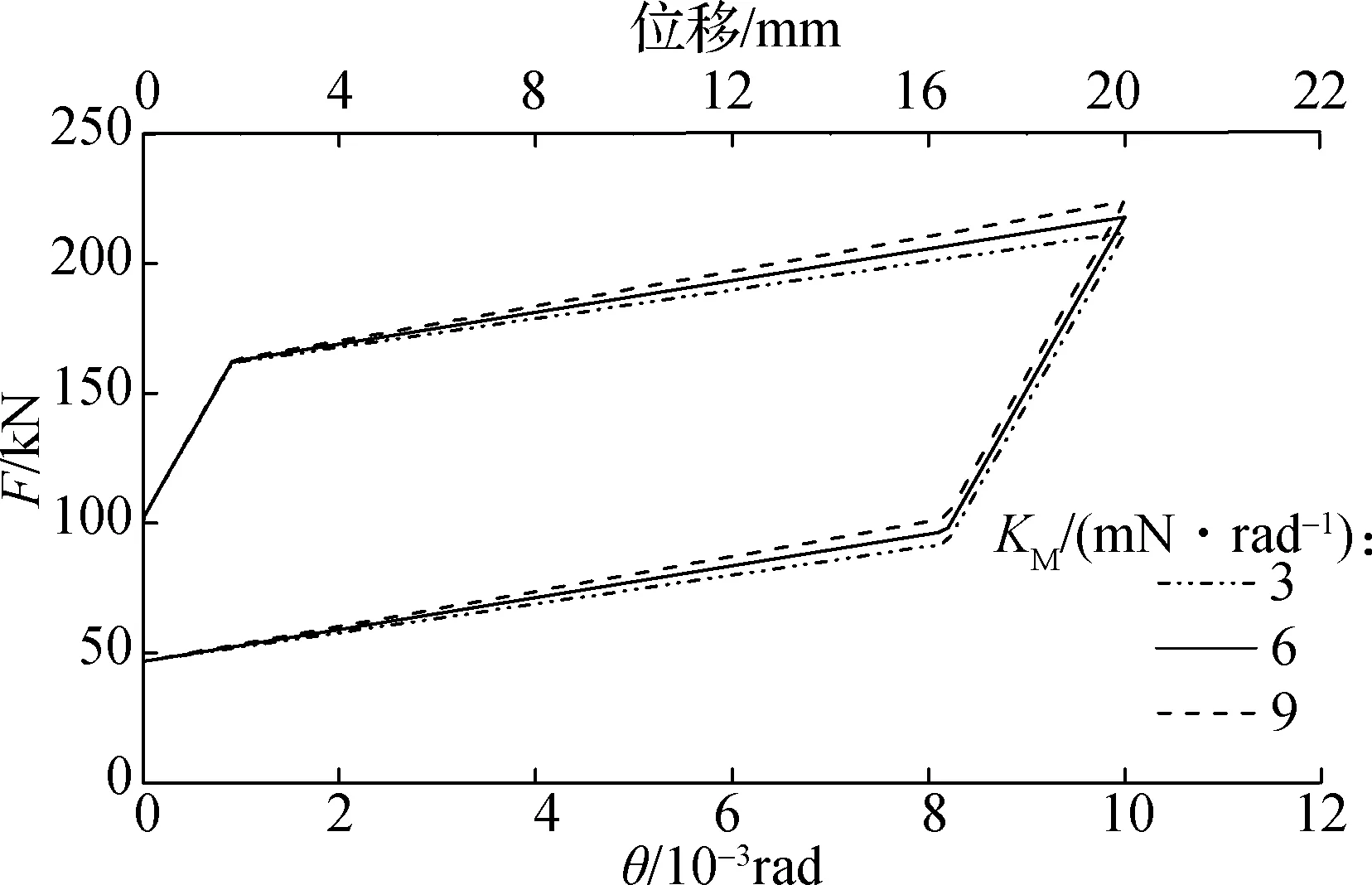
图10　不同角部材料下的摇摆墙滞回曲线

不同初始预应力P0下摇摆墙的滞回曲线见图11.由图可知,增大初始预应力时摇摆墙上摇摆起始点的力变大.结合式(22)和(28)可知,增大初始预应力时墙体滞回曲线仅向上平移,包围面积不变.

不同预应力筋面积SP下摇摆墙的滞回曲线见图12.由图可知,增大预应力筋面积时摇摆墙的摇摆起始点不变,加载和卸载时屈服点的位移均不变,卸载时与坐标轴纵轴的交点不变,摇摆墙滞回曲线包围的面积不变.与标准墙比较,当SP增大25.7%时摇摆墙的屈服前刚度增大1.9%,屈服后刚度增大20.8%;SP减小24.6%时摇摆墙的屈服前刚度减小1.8%,屈服后刚度减小19.9%.

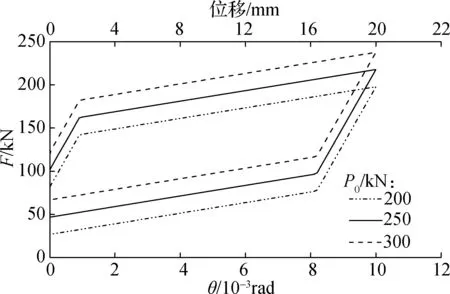
图11　不同初始预应力下的摇摆墙滞回曲线

图12　不同预应力筋面积下的摇摆墙滞回曲线

4　结论

1) 将穿过墙体的预应力筋锚固于连接梁上,可比锚固于摇摆体顶部获得更大的自复位力.初始预应力越大,摇摆起始荷载越大,复位时残余变形越小.

2) 将矩形摇摆体4个角部替换为高延性的弹性材料,摇摆体在转动过程中对主体结构的影响减小.替换材料的刚度越大,损伤可控摇摆墙的刚度越大,摇摆支撑点的应力集中越小.

3) 增大剪切阻尼器的刚度和屈服力可显著提高损伤可控摇摆墙的耗能,但阻尼器屈服力过大则会影响自复位性能.

4) 实际工程中为保证损伤可控摇摆墙抗滑移的可靠性,需要附加构造措施.

参考文献(References)

[1] Housner G W. The behavior of inverted pendulum structures during earthquakes[J].BulletinoftheSeismologicalSocietyofAmerica, 1963,53(2): 403-417.

[2] 周颖, 吕西林. 摇摆结构及自复位结构研究综述[J]. 建筑结构学报, 2011, 32(9): 1-10.

Zhou Ying, Lü Xilin. State-of-the-art on rocking and self-centering structures[J].JournalofBuildingStructures,2011,32(9): 1-10. (in Chinese)

[3] Eatherton M R, Hajjar J F, Deierlein G G, et al. Controlled rocking of steel-framed buildings with replaceable energy-dissipating fuses[C]//The14thWorldConferenceonEarthquakeEngineering. Beijing, 2008:1-8.

[4] Gu M, Pang W, Schiff S. Displacement design procedure for cross laminated timber (CLT) rocking walls with sacrificial dampers[C]//Proceedingsofthe2015StructuresCongress. Oregon, Portland: ASCE, 2015: 2777-2791.DOI:10.1061/9780784479117.241.

[5] 胡晓斌, 贺慧高, 彭真, 等. 往复荷载作用下自复位墙滞回性能研究[J]. 建筑结构学报, 2013, 34(11): 18-23.

Hu Xiaobin, He Huigao, Peng Zhen, et al. Study on the hysteretic performance of self-centering wall subjected to reversal loading[J].JournalofBuildingStructures, 2013,34(11): 18-23. (in Chinese)

[6] Roh H S. Seismic behavior of structures using rocking columns and viscous dampers[D]. Buffalo, USA: Department of Civil, Structural and Environmental Engineering, University at Buffalo, the State University of New York, 2007.

[7] Roh H, Reinhorn A M. Analytical modeling of rocking elements[J].EngineeringStructures, 2009,31(5): 1179-1189. DOI:10.1016/j.engstruct.2009.01.014.

[8] Roh H, Reinhorn A M. Nonlinear static analysis of structures with rocking columns[J].JournalofStructuralEngineering, 2010,136(5): 532-542. DOI:10.1061/(asce)st.1943-541x.0000154.

[9] Roh H, Reinhorn A M. Modeling and seismic response of structures with concrete rocking columns and viscous dampers[J].EngineeringStructures, 2010,32(8): 2096-2107. DOI:10.1016/j.engstruct.2010.03.013.

[10] Preti M, Meda A. RC structural wall with unbonded tendons strengthened with high-performance fiber-reinforced concrete[J].MaterialsandStructures, 2013,48(1): 249-260. DOI:10.1617/s11527-013-0180-8.

[11] 吕西林, 陈云, 毛苑君. 结构抗震设计的新概念——可恢复功能结构[J]. 同济大学学报 (自然科学版), 2011, 39(7): 941-948.

Lü Xilin, Chen Yun, Mao Yuanjun. New concept of structural seismic design: Earthquake resilient structures[J].JournalofTongjiUniversity(NaturalScience), 2011,39(7): 941-948. (in Chinese)

[12] 郝建兵. 损伤可控结构的地震反应分析及设计方法研究[D]. 南京: 东南大学土木工程学院, 2015.

[13] 党像梁, 吕西林, 周颖. 底部开水平缝预应力自复位剪力墙试验设计及结果分析[J]. 地震工程与工程振动, 2014, 34(6):103-112.

Dang Xiangliang, Lü Xilin, Zhou Ying. Experimental design and measured behavior analysis of self-centering shear walls with horizontal bottom slit [J].JournalofEarthquakeEngineeringandEngineeringVibration, 2014,34(6): 103-112. (in Chinese)