轨检车车体横向加速度的判定与分析

陆贤斌　中国铁路上海局集团有限公司工务处

1 前言

轨检车是当今轨道检查最为科学准确的检测工具，是指导工务部门养护维修的重要依据。随着线路状态的不断提升，轨检车的检查数据也有大幅度的改善，同时轨检车检测数据各项扣分的比重也发生了明显的变化。

以前轨检车的检测数据主要以几何尺寸为主，三角坑、高低、轨向、轨距为主要扣分项目；但随着线路质量的不断提升，几何尺寸扣分有了明显的下降，然而横向加速度的扣分比重却有明显的上升，现就通过分析轨检车横向加速度出分的原因来减少横向加速度扣分。

轨检车的横向加速度是反应车体运行过程中水平受力的综合指标，其大小不仅受线路的几何尺寸影响，还与线路的曲线参数，钢轨状态和列车的运行情况等有关。现结合检测车波形图对横向加速度进行判定和分析，针对不同线路状态，找出合理的整修方法从而减少横向加速度扣分。

2 曲线地段

曲线地段是横向加速度出分最多的地段，占了横向加速度整体扣分的一大半以上。由于我国既有线客货混运的特征，曲线超高的设置本身就会造成横向加速度扣分，关于该部分横向加速度扣分的取舍，现结合轨检车检查中的实际情况加以分析。

2.1 曲线地段无几何尺寸病害时

如图1为曲线超高引起横向加速度的波形图，该段线路基本没有几何尺寸扣分，但出现了大量的0.07g左右的横向加速度扣分，现就这些横向加速度扣分进行分析。

我国工务部门常用的超高设置公式为：（1）式中：h--曲线的设置超高(mm)；

R--曲线半径(m)；

v--通过列车的平均速度(km/h)。我国的既有线具有客货混运的特点，所以在设置曲线超高的时候既要满足高速客车，同时也要考虑低速货车。在设置曲线超高时，平均速度应为该曲线一昼夜所有通过列车速度的加权平均数。同时曲线超高的设置必须满足《维规》中规定的线路允许速度、列车平均速度对过(欠)超高和的要求。

图1 超高引起横向加速度的波形图

如图1所示，当轨检车通过曲线时，产生的横向加速度为：

式中：h--曲线的超高(mm)

g--重力加速度；

s--两钢轨中心距。

通过公式(1)和(2)得，曲线欠超高：

考虑到车辆弹簧系数，我们假设为β，一般取值为0.2：

从公式我们可以得出，每13个mm的过（欠）超高就会对列车产生0.01g的横向加速度。在2006版《铁路线路修理规则》中规定，未被平衡的欠超高不应大于75mm，困难情况下不应大于90mm，但允许速度大于120km/h线路个别特殊情况下不应大于110mm；未被平衡的过超高不应大于30mm，困难情况下不应大于50mm，允许速度大于160km/h的线路个别特殊情况下不应大于70mm。而轨检车横向加速度扣分I级为 0.06g，II级为 0.09g，III级为 0.15g如表1。

表1 过（欠）超高对应横向加速度表

从表1我们可以看到，在欠超高允许范围内，就有可能产生I级的横向加速度，有些特殊地段接近II级超限；在过超高特殊情况时，也会产生接近I级的横向加速度。图1的波形图就是轨检车通过曲线时，由于过超高产生的横向加速度，结合实际检测情况，我们发现横向加速度往往略大于表1的理论值。对于该部分的横向加速度，轨检车工作人员可以适当的删除部分I、II级横向加速度。由于超高的设置条件，工务部门不能避免该横向加速度扣分，但针对这样的曲线，应尽量将圆曲线做圆顺，从而减少横向加速度的扣分个数，降低扣分。

2.2 曲线地段出现轨向超限时

如图2为当曲线地段出现轨向超限时，引起横向加速度扣分的波形图。

图2 轨向引起横向加速度的波形图

为了方便对横向加速度的分析，我们可以把曲线和轨向对轨检车产生的横向加速度分开计算，而实际的横向加速度为两者的叠加效果。

曲线对轨检车产生的横向加速度为：

轨向对轨检车产生的横向加速度，我们可以将轨向看作是另一段曲线，根据（fy、λ、R均以m计)，得出R=500λ2/fy。

式中，fy--轨向不平顺值，mm；

R--曲线半径，m；

λ--轨向半波长，m。根据圆周运动原理，在此处产生的横向加速度为

式中的a为轨向产生的实际水平加速度，g；v为轨检车速度km/h；fy为轨向不平顺，mm；β为弹簧附加系数，一般取0.2；λ为轨向不平顺的半波长，m。

为了更直观的了解轨向产生横向加速度的大小，我们假设轨向的半波长为5m，120区段的速度我们取110km/h,160区段的速度我们取140km/h，根据《维规》中的 I、II、III级轨向的超限可算出产生的横向加速度．见表2。

表2 轨向对应的横向加速度表

当曲线上出现轨向时，对轨检车产生的横向加速度为：

结合表1和公式我们发现，当曲线上出现轨向超限时，必然会产生较大的横向加速度，所以在日常养护中，应特别注意曲线上轨向病害的防治。

2.3 曲线地段出现轨距超限时

由于我国既有线客货混运，每条曲线对于通过列车不可避免的存在过超或欠超的问题，这也导致了大部分曲线侧磨严重，曲线位置大轨距病害较为普遍。曲线上的大轨距是造成曲线横向加速度扣分的主要原因。如图3曲线地段大轨距引起横向加速度的波形图，圆曲线部分普遍存在8mm左右的大轨距，列车通过时，产生大量0.09g左右的横向加速度超限。

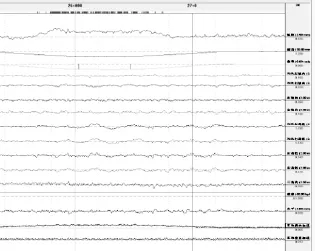
图3 大轨距引起横向加速度的波形图

轨距超限对列车产生的横向加速度类似于轨向，计算公式为：

同样我们假设轨向的半波长为5m，120区段的速度我们取110km/h,160区段的速度我们取140km/h，根据《维规》中的I、II、III级轨向的超限可算出产生的横向加速度（见表3）。

表3 轨距对应横向加速度表

当曲线上出现轨距时，对轨检车产生的横向加速度为：

结合实际检测，我们发现轨距的波长往往较长，所以产生的横向加速度往往比表2的数据小，但当曲线位置出现大轨距时，由于两者的叠加，也会产生大量的横向加速度扣分。曲线位置由于大轨距引起的横向加速度扣分是我们日常检查中横向加速度主要的出分原因。对于该部分的横向加速度，应尽量减小大轨距超限，对于侧磨严重的曲线应及时更换，同时尽量将曲线做顺，从而减少横向加速度扣分。

2.4 曲线地段出现水平超限时

当曲线地段出现水平超限时，如图4为曲线地段高低引起横向加速度的波形图，圆曲线上有一处8mm的高低超限，同样把曲线和水平对轨检车产生的横向加速度分开计算。

图4 水平超限引起横向加速度的波形图

曲线对轨检车产生的横向加速度为：

曲线上的水平对轨检车产生的横向加速度我们可以把水平看做曲线上的过（欠）超高对列车产生的横向加速度，根据圆周运动原理产生有水平加速度(a以m/s2计)，把(v以km/h计,)代入上式得水平加速度为：；考虑机车弹簧压缩则实际水平加速度为

根据《维规》中的水平的I、II、III级超限，得表3

表4 水平超限对应横向加速度表

所以曲线上出现水平超限时，对轨检车产生的横向加速度为：

相对轨向和轨距来说，水平产生的横向加速度相对较小，但由于曲线本身过超或欠超对列车产生了一定的横向加速度，再叠加水平超限产生的横向加速度，同样有可能产生横向加速大值超限。

2.5 曲线地段出现轨向、轨距、水平逆相位复合不平顺时

当曲线地段同时出现轨向、轨距、水平超限中任意逆相位复合不平顺时，这时我们应该特别注意，由于横向作用力的相互叠加，往往会产生横向加速度大值超限。如图5为曲线地段复合不平顺引起横向加速度的波形图及对应超限。

图5 复合不平顺引起横向加速度的波形图

图6 复合不平顺及横向加速度扣分

从图5和图6我们发现，在曲线上同一地点同时出现轨距、高低、轨向的逆相位复合不平顺时，虽然几何尺寸超限都只有Ⅰ、Ⅱ级，但叠加的横向加速度却达到了0.17g的Ⅲ级超限。曲线上出现逆相位复合不平顺时，其计算公式为：

当曲线上出现逆相位复合不平顺时，由于产生的横向加速度的相互叠加，往往会产生Ⅲ级超限，所以工务部门应特别重视曲线地段逆相位复合不平顺的整治，避免大值超限。

3 直线地段

直线地段横向加速度相对来说比较少，但一旦出现横向加速度大值，就应特别注意。由于单一的水平不平顺不会对列车产生横向加速度，所以直线地段的横向加速度主要是由轨向、轨距以及逆相位复合不平顺引起的。直线地段由于轨距、轨向以及逆相位复合不平顺引起的横向加速度的计算公式我们可以参照曲线地段的计算公式。其中以逆相位复合不平顺引起的横向加速度最为严重。

4 道岔地段

道岔地段也是经常产生横向加速度的主要处所，从日常检查中发现，当轨检车高速直向或侧向通过道岔时，往往会产生不同程度的横向加速度，这主要和道岔地段相对复杂的结构病害有关。

当轨检车直向通过道岔时，横向加速度主要是由道岔的结构病害造成的，主要有基本轨曲折点不符合标准，尖轨不密贴，护轨方向不顺等，除了结构病害，道岔上的轨向也是引起横向加速的的主要原因

当轨检车侧向通过道岔时，往往会产生比较大的横向加速度，如图7为列车侧向通过道岔时出现横向加速度的波形图。

图7 侧向过岔引起横向加速度的波形图

这种情况在我们平时的检测中经常遇到。侧向过岔的运动轨迹类似于一条曲线，我们可以看作是列车通过曲线来计算产生的横向加速度，公式为：，由于重力的水平分力几乎为零，所以列车产生的向心加速度a即为横向加速度。当通过道岔的速度过快时，必然产生较大的横向加速度。

5 结论

（1）横向加速度的扣分主要集中在曲线上，由于我国既有线客货混运，曲线本身的超高设置就可能引起横向加速度Ⅰ级超限。

（2）当曲线上出现几何超限时，其产生的横向加速度与超高引起的横向加速度相互叠加，造成横向加速度大量扣分。其中曲线上的大轨距超限是引起横向加速度扣分最多的几何超限。

（3）在日常检查中，应特别注意逆相位复合不平顺，由于横向加速度的相互叠加，Ⅰ、Ⅱ级的几何超限往往会产生横向加速度大值，特别是曲线地段的逆相位复合不平顺。

（4）道岔地段经常出现横向加速度大值超限，主要原因是道岔的结构病害以及侧向过岔速度过快引起的，在日常检查中，应特别注意道岔区段的检查。

[1]邓学通.《准高速轨检车检测原理及应用》.中国铁道出版社，2004（8）.

[2]王金报,戚昌宪等.《铁道工务》.中国铁道出版社.2003.

[3]汪勤,吴纪才.《轨道复合不平顺权重系数的求解方法》.《铁道标准设计》.2005.

[4]许玉德.《轨道不平顺预测理论及辅助决策系统的研究》.北京交通大学.2003.