棉花叶面积的速测方法研究

黄光伟，翟云龙，吴全忠，陈国栋

（塔里木大学植物科学学院，新疆 阿拉尔 843300）

叶片是植物重要的营养器官和蒸腾器官，叶面积是植物进行光合作用、蒸腾作用、呼吸作用及产量构成因素的重要指标之一，叶面积的大小、发育状况和受虫害程度对作物的生长发育、产量和产品质量有较大的影响[1]，也是对作物进行合理栽培管理监测的重要手段[2]，生产中常用叶面积指数来衡量作物群体的生长状况，并以此作为确定栽培措施的参考指标。

目前测定叶面积指数的方法有很多，大致可以分为2类，第一类为直接测定叶面积指数，第二类为间接测定叶面积指数。棉花叶面积的实体测量是试验中非常耗时的一项工作，王家保[3]等对方格计算法、求积仪法、直接称重法、画纸称重法和回归方程法进行了比较分析，不同方法叶面积的最终测定结果之间无显著差异，这一结果在卢美英[4]等的研究结果中也得以证实。棉花叶片的活体测量是试验中经常做的工作，回归方程和系数法不必摘叶可活体测定，有一定的实用价值；杨劲峰[5]等和张恒敢[6]等详细介绍了使用Matlab、Photoshop 等软件测定叶面积的原理，这些研究对建立快速、便捷、精确测定叶面积的方法具有积极的推动作用。目前对作物活体叶面积的测定多采用长宽系数法，棉花叶片的长度易测定，而叶片宽度的标准不易掌握，本试验的目的旨在寻求快捷的棉花活体叶面积测定的简易方法，为棉花长势的监测与产量估算提供依据。

1 材料与方法

试验于2015年在塔里木大学进行，试验材料来自塔里木大学校内作物圃种植的海岛棉品种，以棉株各个部位的棉叶共计210 片叶片为供试材料。将叶片的轮廓描绘在标准纸（打印纸）上，按叶形沿轮廓线剪下得到纸模，在电子分析天平上称得纸模重量，将此重量除以单位面积标准纸重，即得到纸模面积（叶面积）。

2 结果与分析

2.1 叶长与叶宽的乘积与叶面积的关系

以叶长与叶宽的乘积为自变量，以叶面积为依变量，进行函数模拟，结果表明（表1），棉花叶片叶长与叶宽的乘积与叶面积的函数关系可用线性、二次等多种函数关系进行描述，综合比较可以看出，以线性函数关系回归方程的模拟效果最好，相关系数r 为0.942 3，相关性极显著。

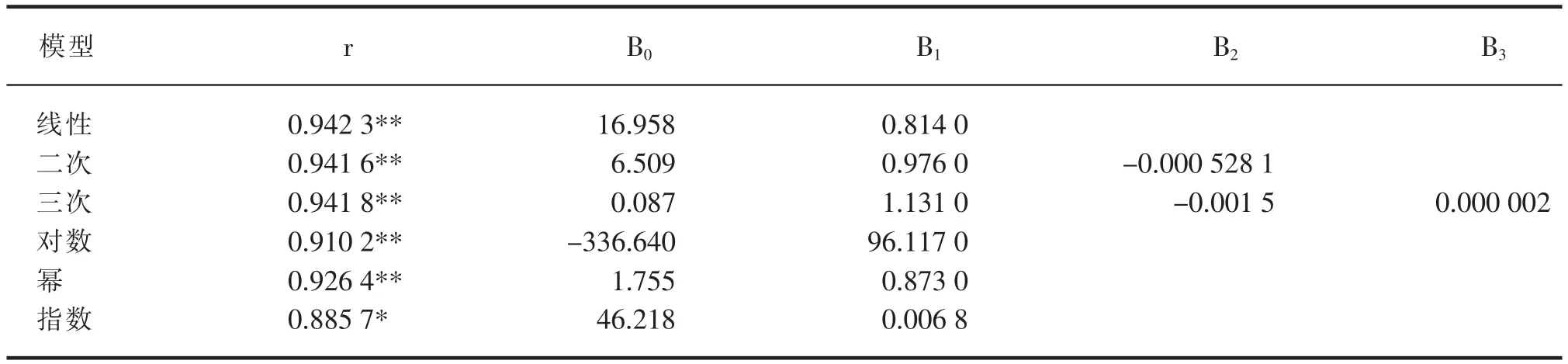
表1 叶长与叶宽乘积（X）与叶面积（Y）的关系

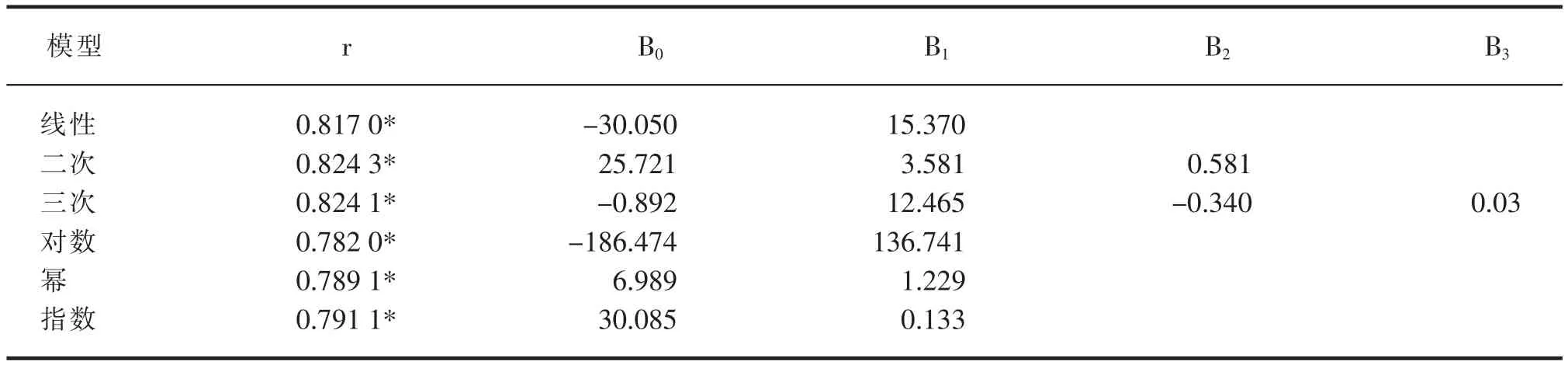
表2 叶宽与叶面积的关系

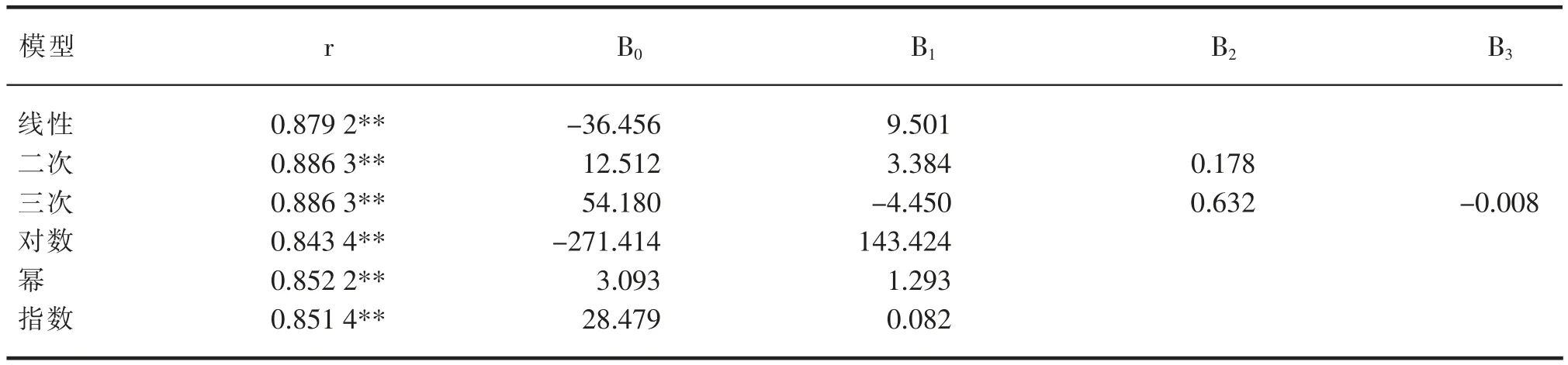
表3 叶尖距与叶面积的关系

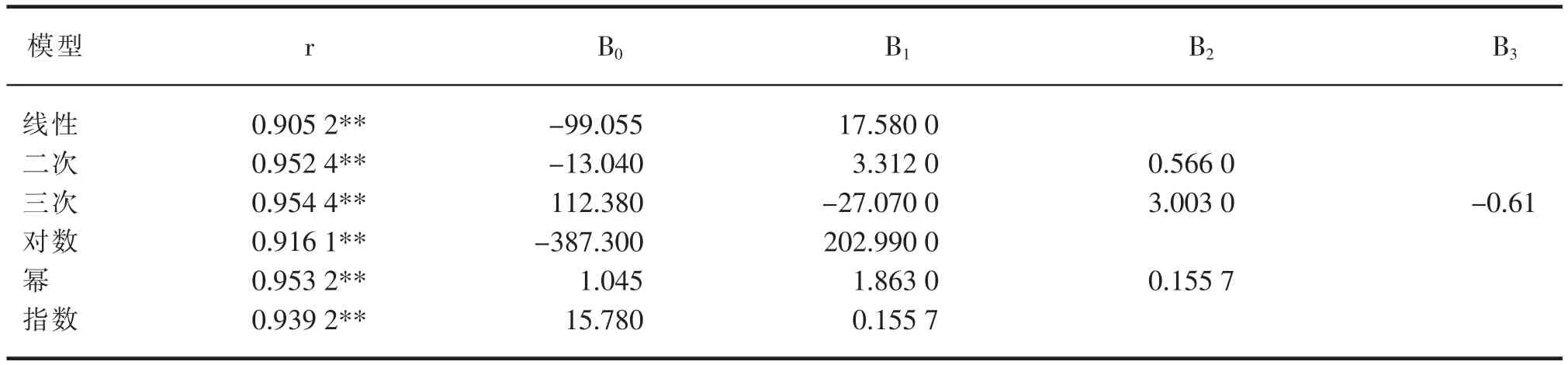
表4 叶长与叶面积的关系

2.2 叶宽与叶面积的关系

以叶宽为自变量，以叶面积为依变量，进行函数模拟结果表明（表2），棉花叶宽与叶面积的函数关系可用线性、二次等多种函数关系进行描述，但其精确度不如叶长与叶宽乘积（X）与叶面积（Y）的函数方程，其中以二次函数关系回归方程的模拟效果最好，相关系数r 为0.824 3，相关性显著。

2.3 叶尖距与叶面积的关系

以叶尖距为自变量，以叶面积为依变量，进行函数模拟结果表明（表3），棉花叶片叶尖距与叶面积的函数关系可用线性、二次等多种函数关系进行描述，但其精确度均不如叶长与叶宽乘积（X）与叶面积（Y）的函数方程，其中以二次函数和三次函数关系回归方程的模拟效果最好，相关系数r 为0.886 3，相关性显著。

2.4 叶长与叶面积的关系

以叶长为自变量，以叶面积为依变量，进行函数模拟结果表明（表4），棉花叶片叶长与叶面积的函数关系与叶长、叶宽的乘积和叶面积的函数关系的精确性较为一致，但以三次多项式函数回归方程的模拟效果最好，相关系数r 为0.954 4，相关性极显著。

3 小结

研究表明，棉花叶片的特征值与叶面积有着极密切的函数关系，可利用这种函数关系对棉花叶面积进行测定[7-8]。

本试验结果表明，棉花叶长、叶宽、叶长与叶宽的乘积以及叶尖距与叶面积均存在高度的正相关，其相关系数分别为0.954 4、0.824 3、0.942 3 和0.886 3，由于叶长和叶长与叶宽的乘积与叶面积呈极显著相关，理论上这2个指标都可以作为计算叶面积较为准确的方法。长宽系数法是生产中比较常用的测定叶面积的方法，长宽系数法的长度容易测定，而宽度的测定标准则不好掌握，利用叶长与叶面积的函数关系进行叶面积的测量，即能保证准确性，又可节省时间，较传统的长宽系数法缩短一半以上的时间，因此，为了简化测定程序，建议选用叶长法对棉花叶面积进行测定。

测定叶面积所用的传统方法如打孔称重法、干重法、鲜重法等，这些方法简单、易操作，但费时费工，测定结果的准确性和精确性较低；而现如今利用的高科技仪器测定叶面积的方法，如光电叶面积仪法、激光叶面积仪法、数字图像处理法等，操作复杂，对操作者素质要求较高。利用回归方程法测算叶面积具有操作简便、快捷的优势[9]，本研究条件下，叶长与叶面积的最优拟合方程为y = 112.38x3-27.07x2+3.003x-0.61。