基于机器学习的大雾天气背景下特强浓雾本地化诊断研究*

史达伟，李　超，史逸民，张银意

(1.江苏省连云港市气象局，江苏 连云港 222006；2.江苏省气象台，江苏 南京 210008)

大雾是一种近地面局地性很强的低能见度天气现象，在华东地区四季均可见，多发生在冬季，能够对春运期间的交通状况产生严重影响[1]，是重要的自然灾害之一。大雾天气已被气象部门列入需要发布预警信息的重要气象灾害。

目前大雾天气的预报，常常是由科研业务人员对发生大雾的天气特征与气候特征进行总结归纳，建立经验预报模型，具有较强的主观性[2-3]，亦或是通过数值天气预报模式进行预测，但模式对于雾的预测效果并不能满足社会发展需求。周自江等人对长三角地区浓雾事件进行了气候特征分析，发现仲秋至翌年仲春为浓雾多发季[4]。吴彬贵等人的研究表明，浓雾的发生往往伴随着近地面逆温、微风以及水汽辐合[5]。大雾天气是一种灾害性天气现象，且具有很强的局地性[6-7]，即在大雾天气发生时，相似的气象条件在不同的地理环境中有可能产生不同强度的雾。利用主观的角度诊断大雾天气发生时的天气特征(温度、气压、湿度、风向、风速)很难准确把握不同地理环境的大雾强度，尤其对于能见度小于50 m的特强浓雾。对特强浓雾的准确预测具有重要现实意义，目前对特强浓雾的发生发展问题的探讨和研究相对较少，对于强浓雾的微物理研究相对较多，许多研究成果表明，饱和环境与辐射降温是雾滴增长的主要因素[8-13]。Choularton 等的研究表明仅靠辐射冷却不能产生大的雾滴[14]。科研业务人员判断是否有雾时，难以定性地预报出雾的强度，尤其是影响程度最强的特强浓雾。

机器学习是人工智能领域的重要分支。国内外越来越多的学者将机器学习技术应用于气象的业务科研领域。Zhang等[15-16]利用C4.5算法对西北太平洋台风是否登陆与是否转向做出了预测准确的模型；史达伟等人[17]利用决策树算法对道路结冰建立了准确的预测模型；Geng等人[18]利用有限混合模型算法及分类与回归树算法对于登陆中国热带气旋进行了路径分类及频数的预测，达到了较好的预测效果；David A等人[19]利用Random Forest(RF)算法基于雷达资料、卫星资料以及模式输出资料建立了中尺度对流系统(MCS)的预报模型。机器学习在大雾研究中的应用也日益广泛，近十几年来，越来越多的学者利用支持向量机、神经网络等算法对大雾的预测与诊断进行建模，并且收获了较好的效果[20-22]，然而目前对于算法间效果探讨和比较的文章仍然很少。

鉴于以上背景，本文拟从机器学习的角度去研究分析能见度低于50 m的特强浓雾，希望能找出一些规律，对解决这一业务和科研难点有所助益。文章以连云港地区为例，利用机器学习中几种经典的有监督算法(CART、SVM、ANN)对大雾天气发生背景下的能见度低于50 m的特强浓雾建立基于气象观测要素的诊断模型。绝大多数机器学习算法都是“黑箱”算法，为了能够简单直观描述特强浓雾的诊断模型，本文以算法复杂度较低但可理解程度较高的CART算法为例重点展开讨论。

1　资料与方法

1.1　资料来源

本文利用机器学习对特强浓雾进行研究，考虑到算法对于数据质量要求较高，文章选取2014年1月1日至2016年12月31日的连云港58044站逐小时自动观测资料，较2014年以前的1d人工观测四次的气象观测数据而言，该套资料具有观测密度高，数据质量较好的特点。为了研究大雾天气发生背景下特强浓雾的气象观测要素的特征，文章选取能见度小于1 km时段，相对湿度 ≥ 90% 的逐小时观测资料，选取气温、气压、相对湿度、风速、风向、降水、0 cm地表温度及能见度等观测要素。

1.2　CART算法的基本原理

分类与回归树(CART)算法，由Breinman等人提出，是机器学习中的一种有监督的分类算法[23]。该算法是一种二叉树非参数机器学习算法，适用于离散型变量和连续型变量的分类。若目标属性是离散型变量，那么CART算法生成分类树；若目标属性是连续型变量，则CART算法生成回归树，本文运用的是CART的分类树算法。在分类树的构建中CART选择最小Gini系数的属性作为测试属性，Gini系数越小，样本的纯度越大，分割效果越好。

CART算法首先将数据按升序排序，从小到大以相邻数值的中间值将样本分为两组，然后通过Gini系数计算两组样本中输出变量取值纯度：

(1)

式中：t为节点，K为输出变量的类别数，p(j|t)为节点t样本输出变量取j的概率。当节点样本为同一类别值时，输出变量取值的差异性最小，Gini系数为0，而当各类别概率相等时，输出变量取值差异性最大，Gini系数也最大，为1-1/k。

CART算法利用Gini系数的减少量描述纯度的提升：

(2)

式中：G(t)和N分别为分组前输出变量的Gini系数和样本量，G(tr)、Nr和G(tl)、Nl分别分组后右子树的Gini系数和样本量及左子树的Gini系数和样本量。

按照这种方式，反复计算便可得到纯度提升最多的分割点，即使ΔG(t)达到最大的组限为当前最佳分割点。

CART算法是一种经典的决策树算法，算法结果为一颗展示逻辑判断的倒置树形图(根节点在树顶，叶节点在树底)，与人的思考方式类似，容易理解，方便使用。

2　连云港地区大雾与特强浓雾发生特征的统计分析

连云港市是地处江苏东北部的黄海之滨，属于温带季风性气候。由于地处东部沿海，因而大雾发生规律相对复杂，既有下垫面长波辐射冷却引起的辐射雾，又有由洋面暖湿平流引起的平流雾，还有两者混合生成的辐射平流雾。本文以连云港地区的大雾天气为研究背景对特强浓雾天气的发生发展规律以及诊断模型展开研究。针对连云港地区的大雾天气以及特强浓雾天气的时间分布特征进行统计，对影响连云港地区的大雾天气与特强浓雾天气的气象要素特征进行统计分析，既研究大雾与特强浓雾的发生发展规律，也为下一节诊断模型的建立提供数据特征上的描述。

2.1　大雾与特强浓雾的时间分布特征分析

2014-2016年连云港地区的大雾天气与特强浓雾天气随月份的分布特征如图1所示，大雾天气在全年各月均有发生其中10月份至翌年4月份发生大雾天气的频次较高5-9月份的发生频次较低，大雾天气发生频次最高在12月份，累计发生了162 h的大雾天气，占总发生频次的15%，9月份发生大雾天气的频次最低，仅有累计发生24 h的大雾天气。特强浓雾天气主要发生在春冬季节，7-10月份没有特强浓雾的记录。特强浓雾发生频次最高的月份在12月，共计25 h，占总发生频次的42%。

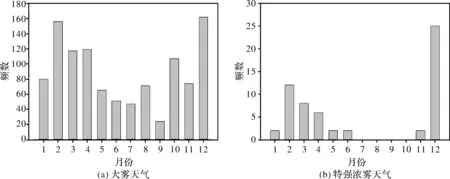
图1　2014-2016年大雾天气与特强浓雾天气的频数的月分布

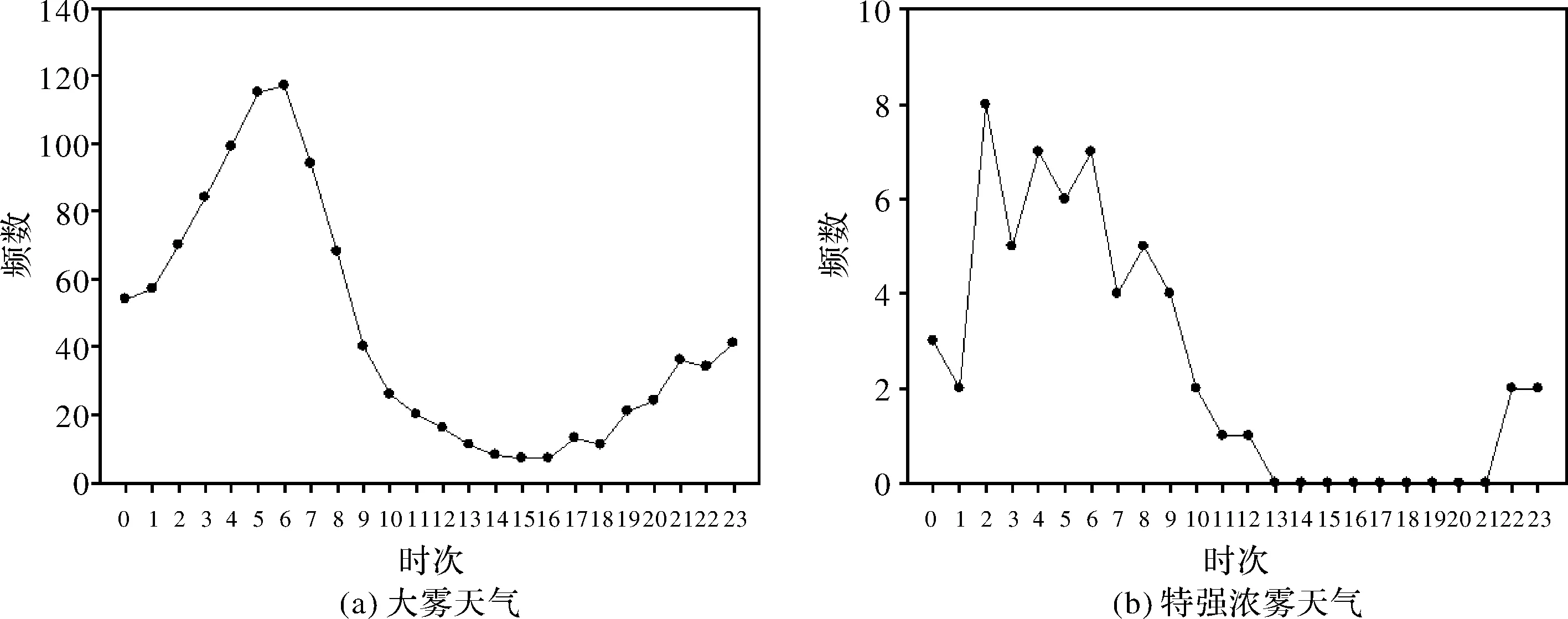
图2　2014-2016年大雾天气与特强浓雾天气的频数的时次分布

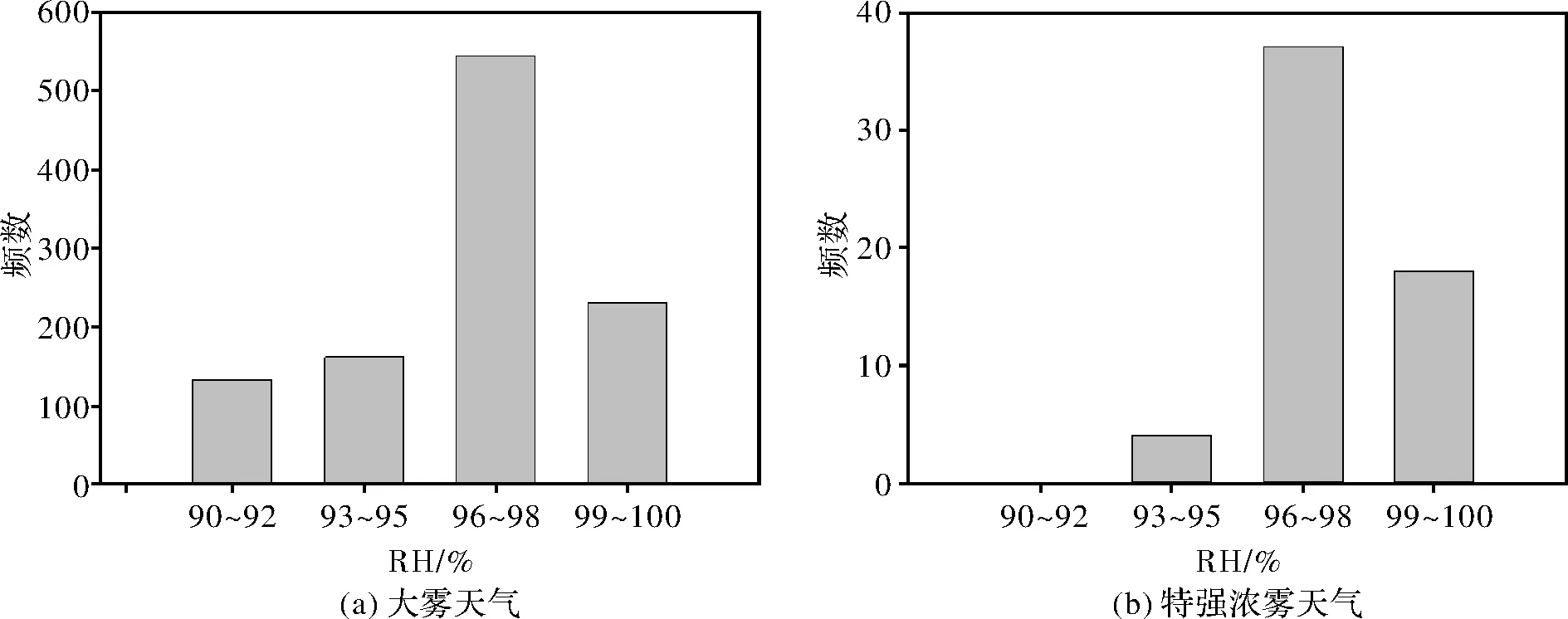
图3　2014-2016年大雾天气与特强浓雾天气频数的相对湿度分布

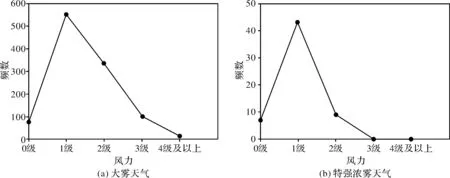
图4　2014-2016年大雾天气与特强浓雾天气频数的风力分布

可以看出，特强浓雾天气较大雾天气的发生具有更强的季节性，冬春季节更易发生，夏秋季节鲜有发生。

大雾天气与特强浓雾天气的时次分布如图2所示，大雾天气在各个时次均有发生，发生时次主要集中在夜晚和凌晨，在午后时段鲜有发生，最常发生的时次在6时，发生过117次，占比11%，而在15、16时发生次数最少均为7次，占比0.6%。观察图2b可以发现，特强浓雾的发生时次主要集中在午夜至上午，而在13时至21时不曾发生过特强浓雾天气，最常发生时次在2时，共发生过8次，占比14%。通过观察对比，大雾天气与特强浓雾天气发生规律较为相似，但是特强浓雾天气发生的时间分布特征较大雾天气更为集中，在冬季和凌晨发生的概率更大。

2.2　大雾与特强浓雾的气象要素特征分析

本节对2014-2016年发生大雾天气和特强浓雾天气时段内相对湿度、风向、风速的统计分析，描述大雾天气及特强浓雾天气发生时段内气象要素的分布特征。

大雾天气及特强浓雾天气发生时相对湿度的分布特征如图3所示，大雾天气在相对湿度90%以上均有分布，主要发生在相对湿度96%～98%这一区间，发生了546个时次，占比51%，而在相对湿度90%～92%这一区间分布最少，发生了133个时次，占比12%。观察图3b可以发现，特强浓雾发生的相对湿度区间分布在93%至100%，90%～92%这一区间没有特强浓雾天气的记录。与大雾天气发生类似，发生时次同样在96%～98%这一区间最为集中，发生了37个时次，占比63%。

相比大雾天气，特强浓雾的发生时的相对湿度区间更窄，并且在相对湿度96%以上这一区间更加集中。

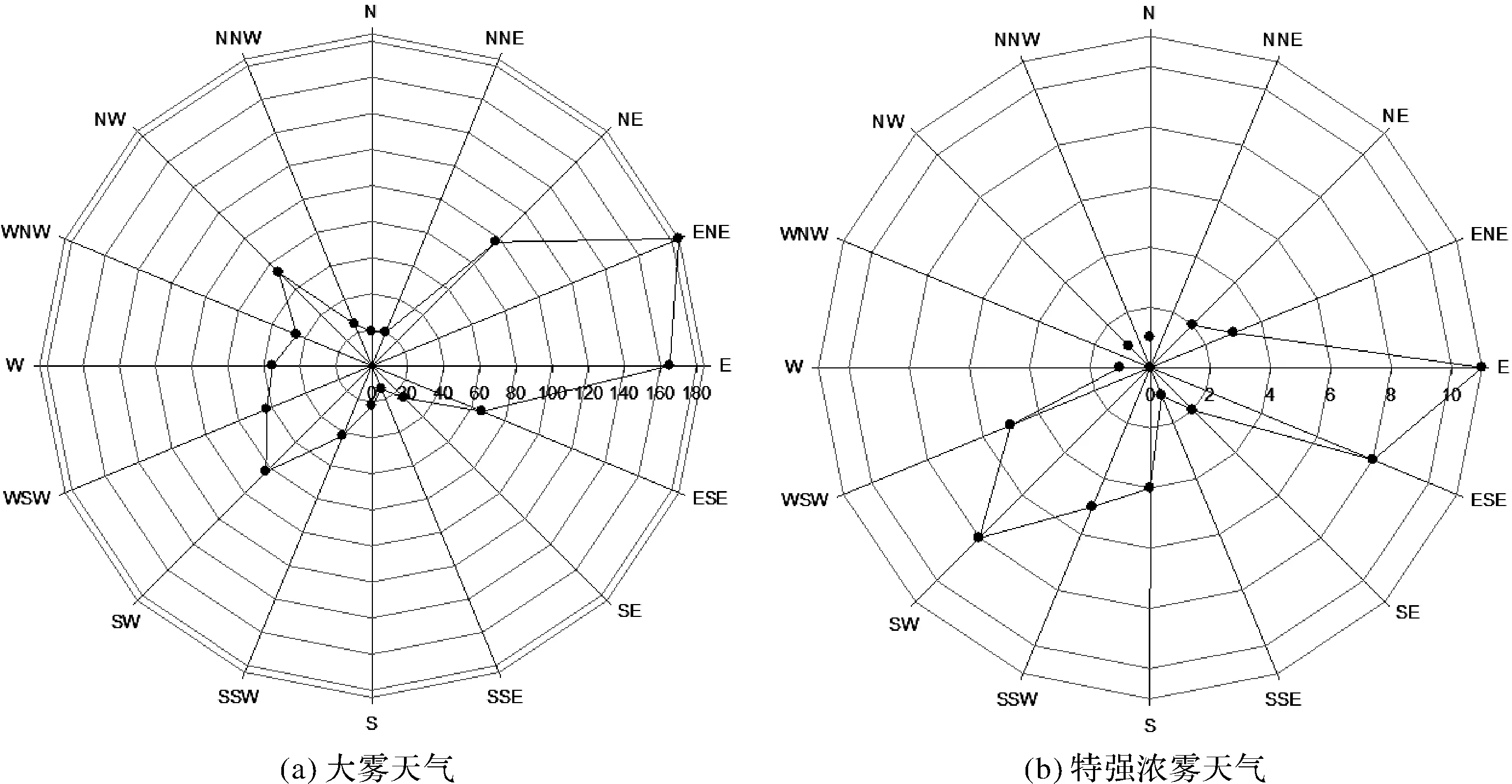
图5　2014-2016年大雾天气与特强浓雾天气频数的风向分布

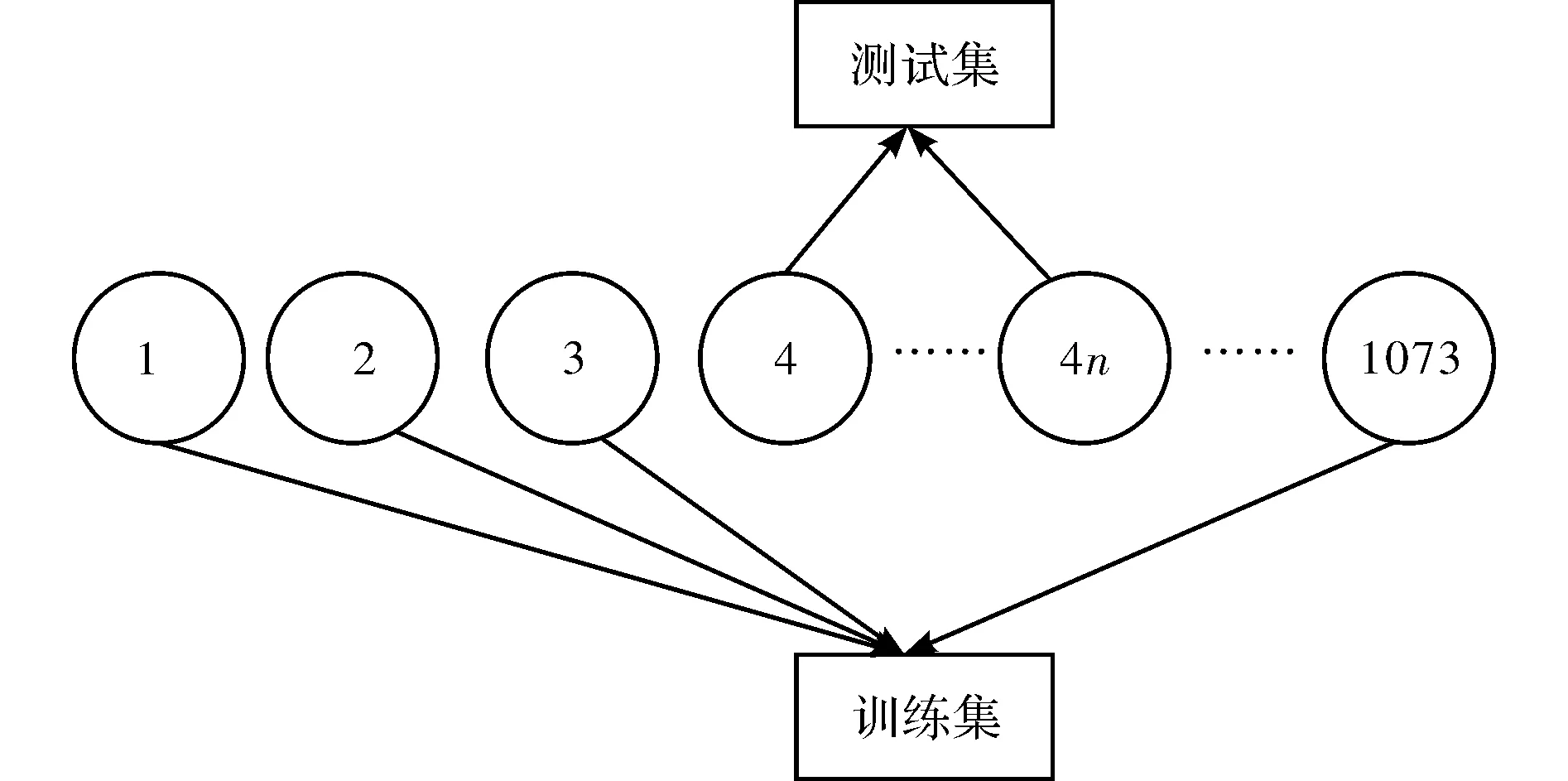
图6　选取训练样本的策略示意图

2014～2016年大雾天气与特强浓雾发生时的风力分布如图4所示，大雾天气发生时，风力从0级至4级及以上均有分布，在风力1级时发生大雾天气的时次最多，有550次，占比51%，风力4级及以上时发生大雾的时次最少，仅有12次，占比1%。从图4b可以看出，特强浓雾发生时次集中在0～2级风，其中风力达1级时发生的频次最多，计43次，占比73%，而当风力达到3级或3级以上时便没有特强浓雾天气的记录。较大雾天气而言，特强浓雾天气具有发生的风力级别区间窄，仅在0～2级风之间有发生，在1级风这一区间样本更加集中等特点。

图5为连云港地区2014-2016年大雾天气与特强浓雾天气发生时段的风向分布。通过观察，可以发现大雾天气发生时，整体以纬向风为主，偏东风场时更有利于大雾天气的发生，发生大雾天气频次最多的风向为ENE，计184个时次，占比17%。观察图5b，可以发现，特强浓雾天气发生时风向以纬向风为主，发生特强浓雾天气频次最多的风向为E，计11次，占比18%，偏北风向时发生特强浓雾的天气状况非常少。

通过观察对比，大雾天气与特强浓雾天气发生时都具有风向偏纬向的特点，偏东风分量作用强于偏西风，这与连云港地区地理位置是东部沿海城市不无关系，偏东风可以从海洋上带来更充沛的水汽。不同的是特强浓雾的发生与否对北风分量更加敏感，当风向出现北风分量时，特强浓雾几乎不会发生，反映了冷空气极不利于特强浓雾天气发生发展，也从侧面反映特强浓雾对暖湿空气输送的要求更高。

通过对大雾天气和特强浓雾天气发生时的特征统计，可以看出在发生大雾天气时，是否能够增强至能见度低于50 m的特强浓雾需要具备以下几个条件更加有利：①季节上，从深秋至翌年春季，冬季更为有利；②时次上，在夜间至早晨，2-8时最为有利；③相对湿度需在93%以上；④风力较弱，但又不是静风状态，1级风最为有利；⑤弱的纬向风和弱的南风分量。

3　基于机器学习算法的特强浓雾诊断模型

通过上节分析总结，可以定性得到特强浓雾的发生发展的有利天气条件，但是特强浓雾天气的发生发展是复杂非线性的天气过程，若希望能够通过这些定性得到的特强浓雾发生的有利条件准确判断特强浓雾是否发生并非易事。因此，本节将利用机器学习中的几种经典有监督分类预测算法，对特强浓雾是否发生建立诊断模型。

3.1　实验数据的预处理

本文使用的机器学习算法均为有标记的有监督算法，该类算法可通过留出法的方式检验模型效果，即将数据样本分为训练集与测试集两部分，并且训练集与测试集为互斥关系，训练集用来建立模型，测试集用于检验模型的泛化能力。一般情况下，训练集占总样本的四分之三左右，余下的约四分之一的样本为测试集。首先，我们将大雾期间“能见度是否低于50 m“抽象成为一个二元分类的问题。经过统计，在2014年1月1日至2016年12月31日发生大雾天气的1 073个时次里，有59个时次发生了能见度低于50 m的特强浓雾。为了维持目标属性量级上的平衡以及尽可能不影响数据原有分布，本文选取测试集的策略为等距离抽样，即以时间为序，将研究样本中每第4n个数据放入测试集，n=1，2，3…(4n<=1073)，仍然以时间为序，其余的数据样本为训练集，如图6所示。

即分别对训练集与测试集进行统计，就训练集而言，共805个数据样本，其中能见度低于50 m的特强浓雾样本为45个，为了维持目标属性“是否为特强浓雾”是与否的平衡，以及模型最后效果更加客观真实，本文针对能见度低于50 m的特强浓雾数据样本采取有放回采样的策略，将特强浓雾数据样本量扩大到与非特强浓雾数据样本量相当(756个特强浓雾数据样本)，利用这种方法不仅可以扩大特强浓雾数据样本规模同时也保证不丢失数据特征。同样地，通过统计发现，在测试集中共有268个数据样本，其中能见度低于50 m的特强浓雾数据样本有14个，采取有放回抽样的策略将测试集中特强浓雾数据样本数量扩大到与非特强浓雾样本数量相当(253个特强浓雾数据样本)，具体如表1所示。这样就完成机器学习所需训练集与测试集的选取与处理，接下来文章将分别利用分类与回归树(CART)算法、支持向量机(SVM)、线性支持向量机(LSVM)以及两种人工神经网络对连云港地区的特强浓雾建立诊断模型。

表1　通过有放回采样方式平衡训练集与测试集二元目标变量样本

3.2　基于CART算法的特强浓雾本地化诊断模型

以是否为特强浓雾为模型的目标变量，模型的输入变量为气温、气压、相对湿度、10 min平均风速、10 min平均风向、降水、0 cm地表温度。将预处理好的训练集输入CART算法，得到决策树(图7)。

决策树形式直观，符合人们逻辑判断的思维方式，从决策树模型可以发现，根节点为气温，换言之，相对于其他强度的大雾天气而言，气温这一属性对于特强浓雾是否发生的影响最为关键。决策树模型中，每从根节点(气温)到一个叶节点(T/F)都可以抽象为一条If…then形式的决策规则，众多规则形成决策规则集(表2)。

通过决策树抽象出判断大雾天气背景下是否会出现能见度低于50m的特强浓雾的规则集。通过训练集数据参与模型的建立，模型整体的学习准确率为90.04%，每条规则都有各自的学习准确率，方便与实际情况对照参考。接着，利用预处理好的测试集数据对模型的泛化能力进行测试，测试准确率为82.25%。通过验证发现，模型整体的分类效果好，泛化能力强。对于大雾天气背景下诊断与预测特强浓雾的发生提供了简洁、可理解、有价值的参考。

3.3　一些其他机器学习算法效果对比

类支持向量机与类神经网络算法同样也是机器学习领域中重要的有监督算法。相比决策树算法而言，这两类算法都具有较高的计算复杂度与较低的算法可理解性，在大多数情况下有着较高的平均准确率。表3是通过预处理的实验数据基于线性支持向量机(LSVM)、支持向量机(SVM)、多层神经网络(MLP)以及径向基神经网络(RBF network)四种算法的实验效果。

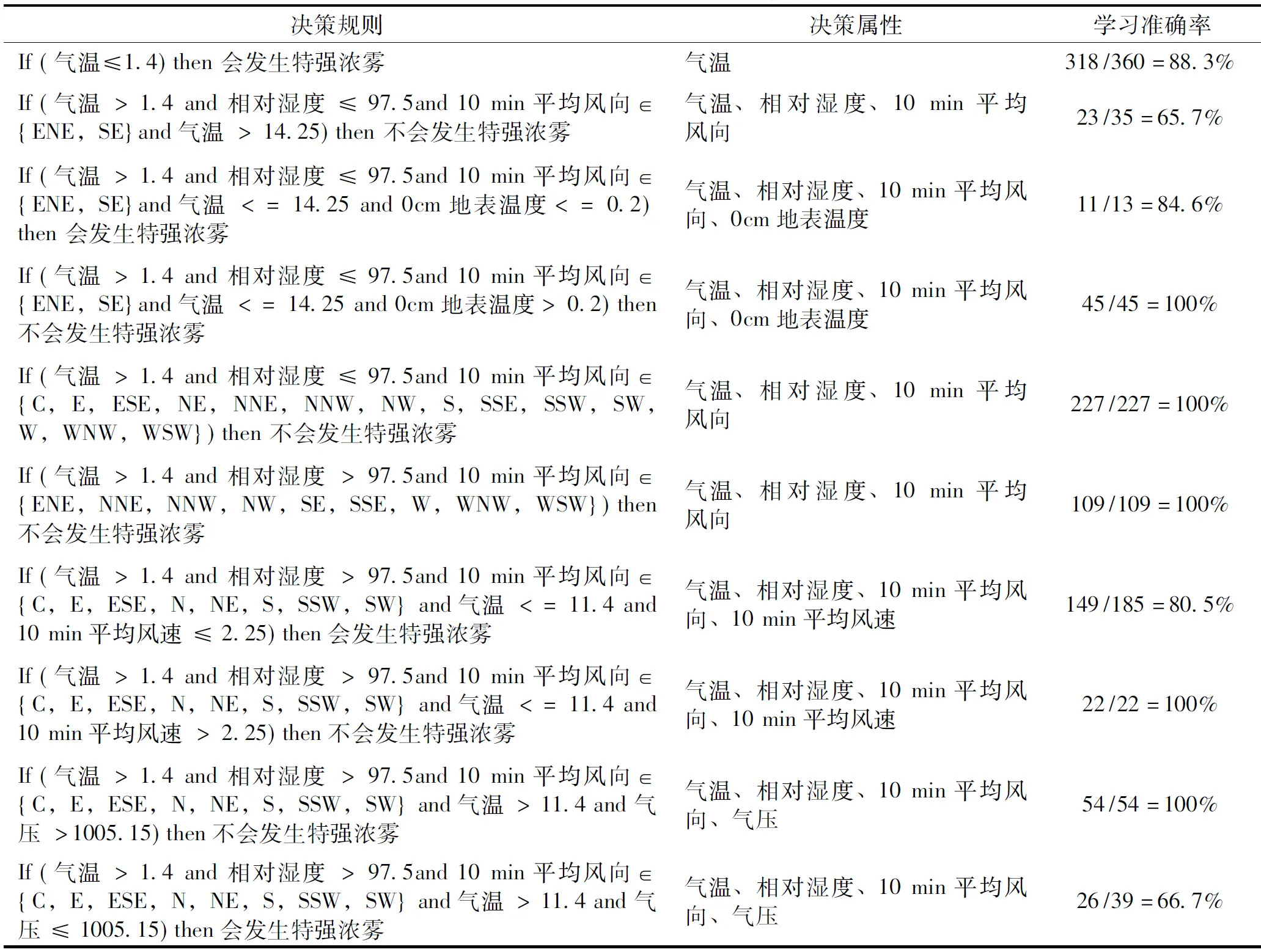
表2　CART算法发现的连云港地区大雾发生背景下特强浓雾气象观测要素特征诊断规则集

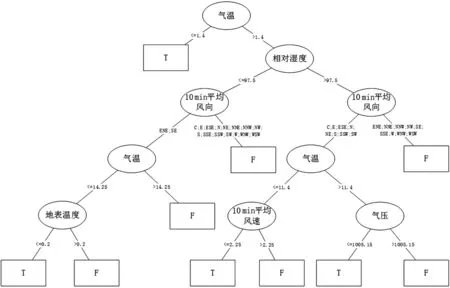
图7　2014-2016年连云港地区大雾发生背景下特强浓雾气象观测要素特征诊断决策树模型

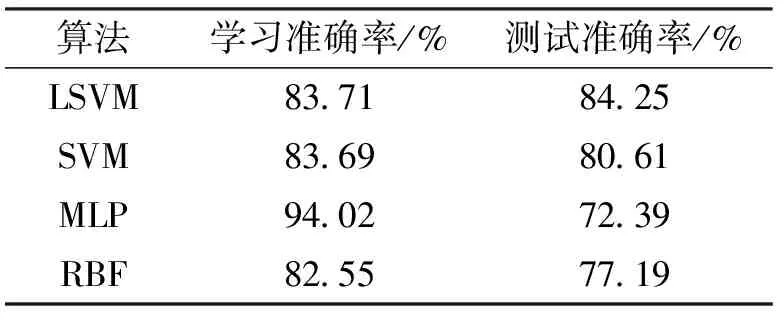
算法学习准确率/%测试准确率/%LSVM83718425SVM83698061MLP94027239RBF82557719

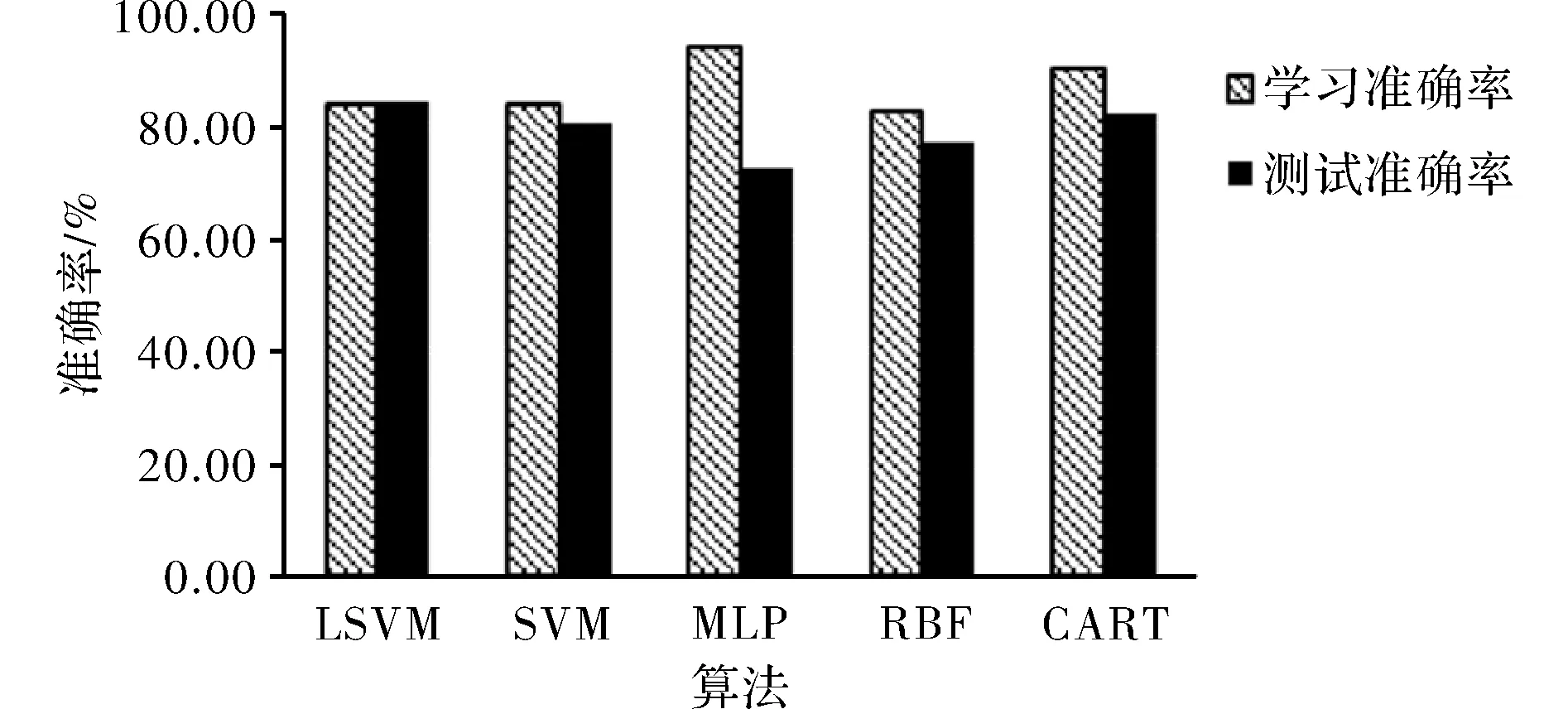
图3　各算法学习准确率及测试准确率

为了方便各算法效果更加直观的对比，我们将包括CART算法在内的五种算法的学习与测试效果绘图，如图3所示，MLP学习效果最佳，但测试效果也最差，存在过拟合的问题较为严重，LSVM的学习效果较CART稍差，但是测试准确率最高，模型泛化能力表现较好。整体上看，类支持向量机算法对于特强浓雾的诊断效果要优于类神经网络算法。

与CART算法不同的是，类支持向量机算法与类神经网络算法具有更高的算法复杂度与很低的算法可理解度，算法收敛速度较慢并且模型难以解释。但是随着计算机计算速度的不断提高，多种机器学习算法并行已经成为可能，利用多种性能优良的算法对同一种目标进行建模，可以相关业务人员提供更加有力的参考。

4　总结

本文针对连云港地区的大雾天气和特强浓雾天气进行了时间特征和气象要素特征的分析，并利用机器学习技术与气象科研业务问题相结合是一种可以尝试的角度。本文利用机器学习技术中的几种有监督算法针对连云港58044站点大雾天气背景下的特强浓雾特征建立了诊断模型，得到以下结论：

(1)通过对连云港地区大雾与特强浓雾天气特征的统计分析，发现特强浓雾相对大雾的发生发展对时间和气象条件有着更加苛刻的要求。

(2)基于CART决策树算法对预处理数据建立的诊断模型可以看出，决策树的根节点为气温，说明在大雾天气发生的背景下气温是判断能否发生特强浓雾的最重要因素；该模型的学习准确率90.04%，测试准确率为82.25%，该模型具有很好的诊断效果以及较强的泛化能力。

(3)CART算法相对于类支持向量机与类神经网络算法而言具有简洁，计算复杂度低，理解直观，准确率较高等特点。

(4)类支持向量机对于大雾天气发生背景下特强浓雾的诊断效果要强于类神经网络算法，与CART算法相比，学习效果稍差，但测试效果较好。

随着计算机性能的不断提高，大数据时代的不断推进，利用人工智能、机器学习技术对自然灾害的发生发展进行预测将成为一种必然发展趋势。然而，多元、海量、异构的数据进行有机融合让算法更易挖掘有用信息，以及算法本身的进一步优化改良同样也是值得思考与研究的问题。

参考文献：

[1]张礼春,朱彬,耿慧,等. 南京一次持续性浓雾天气过程的边界层特征及水汽来源分析[J]. 气象,2013,39(10):1284-1292.

[2]袁成松,梁敬东,焦圣明,等. 低能见度浓雾监测、临近预报的实例分析与认识[J]. 气象科学,2007,27(6):661-665.

[3]冯民学,顾松山,卞光辉. 高速公路浓雾监测预警系统[J]. 中国公路学报,2004,17(3):95-100.

[4]周自江,朱燕君,鞠晓慧. 长江三角洲地区的浓雾事件及其气候特征[J]. 自然科学进展,2007,17(1):66-71.

[5]吴彬贵,马翠平,蔡子颖,等. 辐射雾局地爆发性增强原因探讨[J]. 高原气象,2014,33(5):1393-1402.

[6]丁秋冀,包云轩,袁成松,等. 沪宁高速公路团雾发生规律及局地性分析[J]. 气象科学,2013,33(6):634-642.

[7]高润祥,司鹏,宋明,等. 近50年天津地区局地气候变化特征分析[J]. 气候与环境研究,2011,16(2):159-168.

[7]万齐林,吴兑,叶燕强. 南岭局地小地形背风坡增雾作用的分析[J]. 高原气象,2004,23(5):709-713.

[8]Eldridge R G. A few fog drop-size distribution [J] . J Atmos Sci, 1961,18(5):671-676.

[9]Eldridge R G. Haze and fog aerosol distribution [J]. J Atmos Sci, 1966,23(5):605-613.

[10] Eldridge R G. The relationship between visibility and liquid water content in fog [J]. J Atmos Sci , 1971,28(07):1183-1186.

[11] Goodman J. The microstructure of California coastal fog and stratus [J]. J Appl Meteor , 1977,16(10): 1056-1067.

[12] Pickering K E , Jiusto J E. Observations of the relationship between dew and radition fog [J]. J Geophys Res , 1978,83(5):4-8.

[13] Gerber H. Supersaturation and droplet spectral evolution in fog [J]. J Atmos Sci ,1991,48(48):2569-2588.

[14] Choularton T W , Fullarton G , Lartham J , et al. A field study of radition fog in Meppen , West Germany [J]. Quart J Roy Meteor or Soc , 1981,107(452):381-394.

[15] ZHANG W, LEUNG Y, CHAN J C L, et al. The Analysis of Tropical Cyclone Tracks in the Western North Pacific through Data Mining. Part I: Tropical Cyclone Recurvature[J]. JOURNAL OF APPLIED METEOROLOGY AND CLIMATOLOGY,2013, 52(6):1394-1416.

[16] ZHANG W, LEUNG Y, CHAN J C L, et al. The Analysis of Tropical Cyclone Tracks in the Western North Pacific through Data Mining. Part II: Tropical Cyclone Landfall [J]. JOURNAL OF APPLIED METEOROLOGY AND CLIMATOLOGY, 2013,52(6):1417-1432.

[17] 史达伟,耿焕同,吉辰,等. 基于C4.5决策树算法的道路结冰预报模型构建及应用[J]. 气象科学,2015,35(2):204-209.

[18] Geng H, Shi D, Zhang W , et al. A prediction scheme for the frequency of summer tropical cyclone landfalling over China based on data mining methods [J]. Meterol Appl,2016,23(4):587-593.

[19] David A , James O P , John K W , et al. Probabilistic Forecasts of Mesoscale Convective System Initiation Using the Random Forest Data Mining Technique [J].Wea Forecasting , 2016,31(2):581-599.

[20] 贺皓,罗慧. 基于支持向量机模式识别的大雾预报方法[J]. 气象科技,2009,37(2):149-151.

[21] 李才媛,韦惠红,邓红. SVM方法在武汉市大雾预警预报中的应用[J]. 暴雨灾害,2008,27(3):264-267.

[22] 王彦磊,曹炳伟,黄兵,董兆俊,路泽廷,陈兴明.基于神经网络的单站雾预报试验[J].应用气象学报,2010,21(1):110-114.

[23] Breiman, L, Friedman J H, R Olshen,et al. Classification and Regression Trees[M]. Wadsworth and Brooks.1984.