正定矩阵低秩分解的交替二次规划算法
马婷婷
(辽宁师范大学,辽宁 大连 116000)
在模式识别和机器学习的学习[1-3]中,数据的内在特征结构可以通过矩阵分解得以发现,并且使得数据特征维数很大程度的降了.Lee等[4]发表了非负矩阵分解(non-negativematrixfactorization,NMF)算法,它将一个正定矩阵分解为两个正定矩阵乘积,由于分解后的矩阵是正定的所以只包含非负元素,原矩阵中列向量可称为所有列向量的加权和,矩阵中对应列向量中的元素称为权重系数.因为其分解的结果中都是正数和零即不会有负值出现所以具有非常简便的算法,具有广泛的物理意义,所以可以运用于语音辨识、图像识别、脑电信号提取等等各种问题中[3-6].这篇文章就是将正定矩阵分解算法模型转化为凸二次规划模型求解,从而使处理速度得到了很大的提高。
一、正定矩阵分解的概念与计算
对于m×n阶的实正定矩阵A和正整数k A≈WH(1) 下面就是欧式距离优化模型: 正定矩阵秩分解有很多种的方法[6-11],一般可以分为两种.第一个是优化逼近法.对于模型(2)可以直接采用优化方法求解,可以选择广义既约梯度法、广义乘子法、梯度投影法等的局部最优化方法[11-16].这些方法的优点是算法都比较成熟,收敛性也已经得到证明;但缺点是不能保证全局最优解.也就是说可选择区间方法、微分进化算法、随机投点与随机方向算法等这些全局最优化方法求解[15-16].这类方法的缺点是计算量远大于一般的局部最优化方法。 第二个是公式逼近法,根据式(1),构造出来某种迭代公式,通过同时迭代或交替迭代的方式,将Hk与Wk更新到Hk+1与Wk+1,并希望当k→+∞时,WkHk→A.这种方法优点是,具有很简单的迭代公式,公式中的运算一般简单非常基本的运算等,实现起来非常容易;但是其缺点是收敛性很难得到证明,并且收敛速度比较慢。 在对模型(2)采用局部优化计算时,这里f(x)是一个四次代数多元(p=m×k+k×n个变元)多项式函数,因为其高度复杂的极值点,运用模型(2)这种传统优化算法是很不容易得出结果来的.那么对于这种模型,如果我们令W=W1也就是让W选定为某个常数阵W1,那么有 这是一个关于H的二次规划模型. 具体计算步骤为 步骤1令基矩阵W的初始值为W=Wk(k=1),求Hk(k=1),其中试探性地取参数λ值,然后限制对Hk取值为非负,记下Wk与H”k(k=1)中零元素的个数; 步骤2令H=HK,求Wk+1,得到Wk+1后再一次限制非负的,注意试探性的取值参数μ,使得NWk+1z≥NW”kz,然后再计算总误差E2k(k=1); 步骤3检查是否满足迭代终止条件:若E2k-1≥E2k(k=1)与NW2x≥NW1x同时成立,则令k+1→k继续步骤1,否则停止,那么最优分解就是上一轮的结果. 注:①.初始基阵W1(k=1)的选取方法:只需W1中,尽可能多的零元素存在。无论W1取何值,交替二次规划算法迭代的收敛性都不会受到影响,但如果想要减少迭代次数,那么W1选取得好是至关重要的。 ②.参数λ与μ选取方法:满足以下两个条件即可: (1)从Hk到Hk+1中零元素的个数NHkz到NWk+1z满足NHkz≤NHk+1z; (2)计算出的前后两次总误差值E2k-1到E2k满足E2k-1≥E2k≥E2k+1。 Hk与Wk中元素非负性要求的实现:当模型取(2)这种一般的约束非线性规化时,则模型(2)可行域的边界为H≥0,W≥0。为了上述方法中这些问题出现,这篇文章在交替二次规划迭代计算过程中用零元素代替Hk与Wk中出现的负元素,从而减小了难度。 由于交替二次规划所产生的总误差值列单调递减并且有下界的数列{Ep}(p=1,2,3,…)一定有极限即:E1≥E2≥E3≥…≥Ep≥0,所以算法是收敛的,但是事实上很少算法在有限步终止,我们可以根据WH逼近A的精度E值的要求不同,每一步的结果,都可以作为需要分解的结果。 因为有很多种正定矩阵低秩分解的方法,所以针对同一个问题可以用这些不同的方法,那么又怎样来评定它们的优点和缺点呢?这篇文章的作者认为这就需要存在某些的评定标准,而这个评定标准中主要当然包含三个方面其一为总误差E=Ea+Eb的大小,总误差值当然是越小越好;其二为基矩阵W中列向量W1,W2,W3,…,线性独立的Wi×Wj≈0(i≠j)程度,这种程度是用内积来描述的,当然是越接近0越好;其三为基矩阵W与系数矩阵H稀疏的程度. 交替二次规划算法的提出,这篇文章的优点在于作者注意到了直接求解是非常困难并且非常复杂。所以作者在学习以前别人的基础上,并且满足评定标准中要求,经过长时间刻苦学习与专研给出了解决这样问题的方法。我们通过了大量实际例子都可以了解到,这个方法与上面的要求大致上可以很好的完成。不仅仅算法非常明确,实现起来也很方便,并且由于简单的迭代过程,使得有很小的计算量,这一点对特别是大型数据模型来说是至关重要的,也很容易证明算法的收敛性。 缺点是对Hk与Wk中的元素非负性要求,在迭代过程中如果出现了负元素直接用零元素取代的方案,但是对于普遍性的问题,是否存在特别情况不适用,目前还不是很不清楚,有待进一步的研究。 参考文献: [1]GAO Yuan CHURCHG G.Improving molecular cancer class discovery through sparse non-negative matrix factorization[J].Bioinformatics,2005,21(21):3970-3975. [2]Hoyer P O.Non-negative matrix factization with sparseness constraints[J].TheJournal of Machine Learning Reseaarch,2004,5:1457-1469. [3]“10000个科学难题”数学编委会.10000个科学难题数学卷[M].北京:科学出版社,2009. [4]LeeD D,SeungH S.Learingthepartsofobjectsbynon-negativematrixfactorization[J].Nature,1999,401(6755):788-791. [5]Lee D D,Seung H S.Algorithms for Non-negative matrix factorization[C]// A dvances in Neural Information Processing Systems.Cambridge:MIT Press,2001. [6]蒋娇娇.非负矩阵分解算法的改进及应用[D].北京:北京工业大学,2001. [7]杨洪礼.非负矩阵与张量分解及其应用[D].青岛:山东科技大学,2011. [8]张宇飞.加稀疏约束的非负矩阵分解[D].大连:大连理工大学,2010. [9]赵燕斌.强噪声中诱发电位信号的快速提取研究[D].大连:大连理工大学,2008. [10]郭立.增量式非负矩阵分解方法研究[D].上海:复旦大学,2009. [11]殷海青.图象分析中的非负矩阵分解理论及其最优化和正则化方法研究[D].西安:西安电子科技大学,2011. [12]王德人.非线性方程组解法与最优化方法[M].北京:人民教育出版社,1979. [13]施吉林,张宏伟,金光日.计算机科学计算[M].北京:高等教育出版社,2005. [14]席少霖,赵凤治.最优化计算方法[M].上海:上海科学技术出版社,1983. [15]张可村,李换琴.工程优化方法及其应用[M].西安:西安交通大学出版社,2007. [16]阳明盛,罗长童.最优化原理、方法及求解软件[M].北京:科学出版社,2006.二、正定矩阵低秩分解的交替二次规划算法
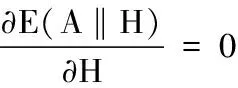
三、交替二次规划算法的收敛性
四、结语

