基于拓扑优化的变速箱壳体轻量化设计

沈　伟，廖　敏,1b，王　强，王　霜,1b，易　军，王川东，何　旭

(1.西华大学 a.机械工程学院；b.流体与动力机械教育部重点实验室，成都　610039；2.四川省机械研究设计院，成都　610063；3.成都主导科技有限责任公司，成都　610091)

0　引言

丘陵地区田块小、不平坦、形状不规则，分布较为分散，地形条件复杂多变[1-2]。大型收割机无法正常使用，而小型联合收割机由于其质量相对较轻和体积相对较小，具有得天独厚的优势[3]。在收获季节，收割机持续工作时间很长，且长期伴随着较大的载荷冲击和振动冲击，特别在高低不平和泥脚较深的田间作业时，变速箱需承受更大的负载，因此对变速箱壳体的可靠性提出了很高的要求。变速箱是整机传动系统的重要部件，为行走动力传动轴系和割台动力传动轴系提供动力。变速箱壳体使内部的轴、轴承、齿轮之间保持正确的相互位置，起到安装和保护的作用，其强度和刚度直接影响传动系统的精度，所以箱体的强度和刚度必须得到保障。然而，在传统对箱体的设计中，为了能够满足箱体的强度和刚度，过度地增大了箱体的壁厚，造成了材料的浪费，增大了箱体的体积和质量，影响了整机的性能[4]。因此，箱体的强度和刚度分析对提其高性能具有重要的实际意义，还能提高整个传动系统和整机的可靠性[5]。

1　变速箱壳体的结构设计

变速箱壳体的结构是由内部零件及内部零件间的相互关系设计而成。变速箱与静液压无极变速器(HST)相连，其动力由发动机输入，具有变速的功能，内部具有行走动力传动轴系和割台动力传动轴系两条轴系，并为收割机行走和割台传动提供动力，还包括收割机转弯刹车和坡上驻车功能，以及变速箱润滑、密封、冷却辅助功能。图1为变速箱工作原理图。

图1　变速箱工作原理

根据变速箱壳体传递的功率和扭矩，采用“结构包容法”，设计的箱体结构如图2所示。其材料选用ZL106铝合金。该变速箱壳体由左右两半壳体装配而成，通过A处凸台螺纹孔用螺钉连接成整体，拨叉安装孔在B处，C处是箱体连接凸台，D处是割台动力输入孔，E处是HST动力输入孔，F处是动力及刹车制动轴承端盖，G处是行走半轴输出孔。

图2　变速箱壳体结构

2　变速箱壳体拓扑优化

2.1拓扑优化理论基础

拓扑优化的基本思想是在特定的区域内寻求材料的最优分布。拓扑优化以材料的“传承载荷的合理路径”为参考，对设计域内的单元进行取舍，实现结构在约束条件下的结构最优设计[6]。利用拓扑优化技术，可以在零部件结构设计阶段给材料合理布局，减轻结构质量，缩短研发周期[7]。

实际工程中，通常先将物理模型转化为数学模型，再利用数学求解方法得到优化结果。现阶段连续体结构拓扑优化的数值方法主要有：均匀化方法、变厚度方法、变密度方法和渐进结构优化法。本文采用变密度法并利用拉格朗日乘子法的求解方法对变速箱壳体进行拓扑优化求解。假定材料密度可变的条件下，把单元密度作为设计变量，将拓扑优化转化为材料优化，用有效用求导方法求解，即

Ke=(Xe)PK0

(1)

其中，Ke为单元的刚度；K0为单元的固有刚度；P为惩罚因子；Xe为结构单元的相对密度。以变速箱壳体的柔顺度最小为目标函数，其数学模型为

Minimize：C(X)=FTD

(2)

X={X1,X2,…XN}T

(3)

(4)

其中，C为结构的柔顺度；F为受到的载荷矢量；D为结构的变形位移矢量；f为剩余材料的百分比；V为结构材料充满的体积；V0为壳体结构设计范围域的体积；V1为密度小于1的材料体积；Xmin为单元相对密度的下限；Xmin为单元相对密度的上限；K为整体刚度矩阵。

2.2变速箱壳体结构的拓扑优化设计

利用ANSYS Workbench 软件中拓扑优化模块对变速箱壳体进行优化，选用四面体和少量的六面体对壳体进行网格划分。以HST输入的最大功率给变速箱施加载荷，充分考虑壳体自重，变速箱壳体主要承受行走动力传动轴系和割台动力传动轴系的轴承力，转弯或者刹车制动时来自摩擦片的相互之间挤压对端盖孔的轴向载荷，壳体所受载荷如图3所示。

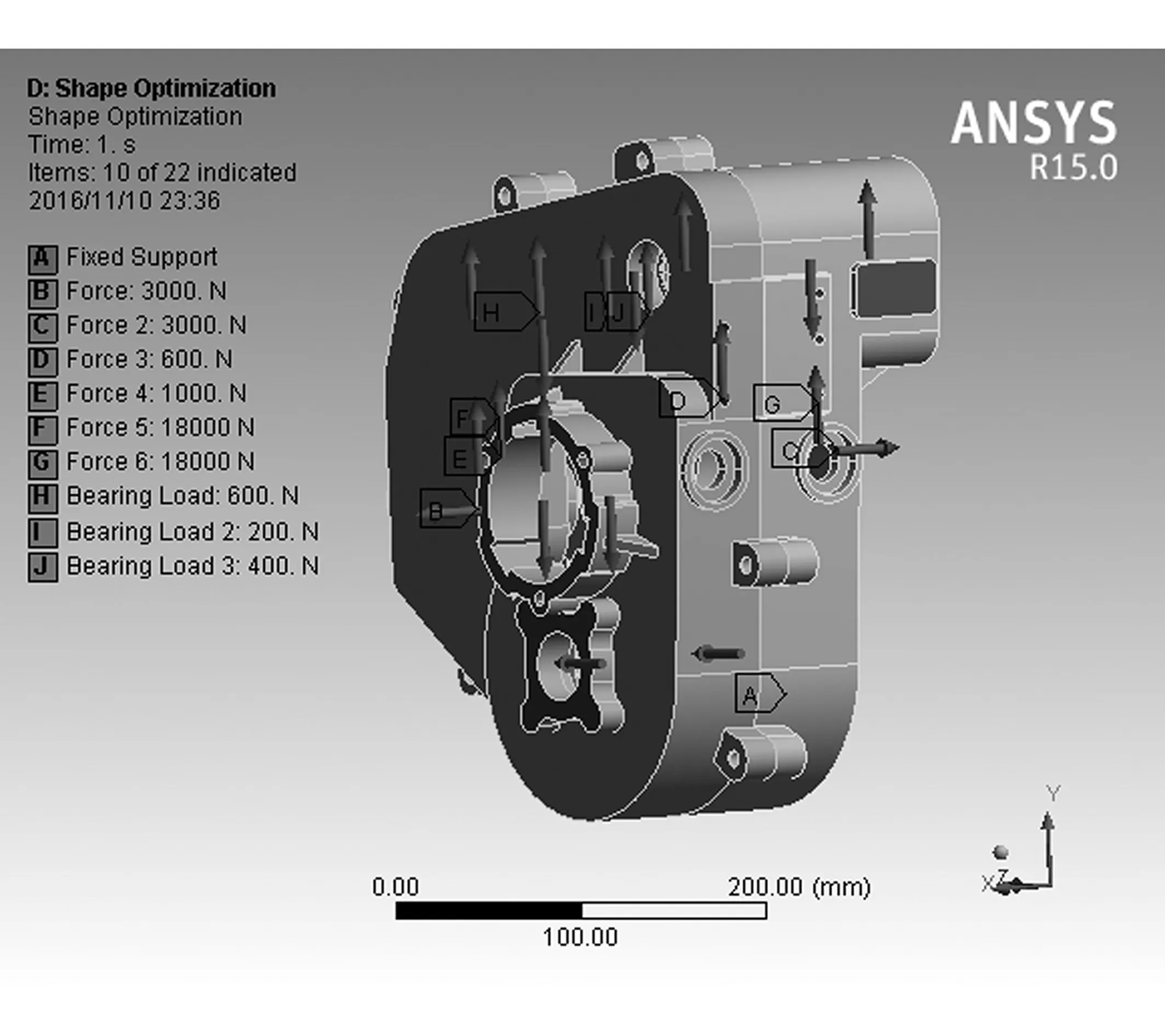
图3　优化域载荷施加

根据多次试验，最后选择去除的材料百分比为70%，壳体左右半壳拓扑优化结果如图4所示。

图4中，Remove表示黑色需要去掉的部分；Keep表示灰色需要保留的部分，也是承受载荷最有效的部分，设计时需要对此部分加强；Marginal表示白色可以保留也可以去除部分，主要分布在行走动力传动轴系和割台动力传动轴系的轴承孔附近区域、壳体的输出轴承孔附近及轴承孔之间的大平面区域。

本文采用在轴承孔周围布置加强筋的方式，并适当减少行走动力传动轴系部分凸台的厚度。考虑大平面处起的承接作用，所以在此处布置弯曲长筋以连接轴承孔周围的加强筋。割台动力输出轴系末端的高速轴轴承孔附近去除材料较多，设计时可适当减少割台输出轴轴承孔凸台部分的壁厚，如图5所示。

图4　左右半壳拓扑优化结果

图5　左右半壳去除材料模拟

3　变速箱壳体结构尺寸优化

3.1响应面方法基本理论

响应面法是用统计学的综合试验技术解决复杂系统的输入与输出的转换关系的方法，能更方便地求解数学优化模型[8]。建立响应面模型有以下步骤：首先试验设计得到样本点；然后构建模型并进行拟合试验；最后得到最优组合解。常用的二阶多项式响应面模型如下式，并采用最小二乘法求解其待定系数，即

(5)

其中，α0、αi、αji为待定系数。若进行K组试验，输入数据为(x1,x2…,xn)i，输出数据g1(x1,x2，…xn)i。 其中，i=1,2,3…,k(k大于或等于待定系数的个数)，xij为第i组输入数据中的第j个数据，可得矩阵

Xa=g

(6)

(7)

a=(α0,α1,…αn,α11,α22,…αnn,

α12,α23,…,αn-1,n)T

(8)

g=(g1,g2,…gk)T

(9)

为了得到更精确的拟合结果，本文对变速箱壳体尺寸优化采用的试验方法是中心复合设计。

3.2变速箱壳体结构尺寸优化模型

1)设计变量：根据变速箱壳体的实际工况，并充分考虑影响壳体质量、刚度、强度的因素，把壳体壁厚T、加强尺寸合理性的约束限制，设计变量存在极限值(见表1)。表1中，筋1截面尺寸、加强筋2截面尺寸作为设计变量。变速箱壳体尺寸如图6所示。图6中，W为加强筋截面的宽度；H为加强筋截面的高度。

表1变量的极限值

Table 1The limit value of the variable mm

设计变量初始值最小值最大值T13713W18412H1528W28412H27212

图6　变速箱壳体尺寸参数

2)目标函数：本文以变速箱壳体的最小质量和最小变形量作为优化目标，具体措施通过改变壳体壁厚T、加强筋截面尺寸W和H来优化箱体结构。

3)约束条件：在寻求目标函数最优的过程中，还需要保证变速箱壳体的工作性能满足使用要求，即最大应力小于80MPa、固有频率大于750Hz，以保证变速箱安全避开收割机的激励频率。

变速箱壳体响应面优化设计模型为

(10)

(11)

其中，f1(x)表示变速箱壳体质量；f2(x)表示变速箱壳体最小变形量；w1i为第i项子目标函数的权因子，主要表示各子目标函数的重要程度；w2i为第i项目标子函数的校正权因子，其目的主要是为了降低各目标子函数之间量级和量纲上的差异[9]。

3.3变速箱壳体响应面结果分析

利用ANSYSWorkbench软件中的响应面优化模块对变速箱壳体的尺寸进行模拟分析，通过中心复合设计法生成了27个设计点，并对每个设计点求解壳体的质量P6、变形量P7、应力值P8和固有频率P9，响应面求解结果如图7所示。

图7　响应面求解结果

完成响应面的拟合后，通过拟合度曲线可以直观分析出实验点与预测点的偏差。如图8所示。

图8　响应面输出参数的拟合度Fig.8　The fitting degree of response

试验中以真实值为横坐标，响应面通过计算的预测值为纵坐标，P6、P7、P9基本上都在中间对角线上，拟合度很高；P8的分布相对对角线有一定的偏移，是由于壳体某些部位存在应力集中，但总体拟合效果较好。通过对输出参数灵敏度的分析，变速箱壳体的壁厚对箱体的质量、最大变形量、最大应力、固有频率具有绝对的影响力，加强筋2的截面宽度也对最大应力的影响较大。针对本文的多目标优化问题，输出目标存在相互制约。从分析可知，变速箱壳体的质量小是以增大最大变形量作为代价的，所以通过权衡得到3个候选设计点，如图9所示。通过对设计参数圆整处理后，再进行一次目标函数的求解结果如图10所示。

图9　设计候选点

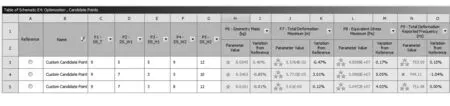
图10　圆整后的候选点

采用综合指数评价法[10]，即

(12)

4　变速箱壳体优化前后静力学对比分析

4.1变速箱壳体有限元静力学分析

根据变速箱壳体的实际结构情况，在轴承孔、油缸安装孔、端盖孔等受力较大的部位选用较小的单元格划分网络，受力较小的次要结构选用较大的单元格。总共划分87 660个单元、149 750个节点，优化前变速箱壳体质量为10.396kg。网格划分后，其约束和载荷情况如下：

1)约束。如图3所示，根据变速箱壳体的实际工况，G处约束箱体的4个自由度，C处约束箱体的另外2个自由度，箱体处于完全约束条件。

2)载荷。变速箱壳体受到的载荷主要是重力载荷、轴承反力、液压缸推力及摩擦片对箱体F处端盖孔的轴向载荷4部分，以HST输入的最大功率给变速箱施加载荷，所受载荷与上文做拓扑优化时一样。

4.2变速箱壳体优化前后静力学对比分析

选择优化前的参数，并对变速箱壳体进行静力学分析，得到壳体在X、Y、Z方向的变形及总变形，如图11所示。由分析可得：壳体在X轴方向的最大变形为0.059 37mm，Y轴方向的最大变形为0.071 911mm，Z轴方向的最大变形为0.042 715mm，总变形的最大变形为0.092 699mm。总体来看，壳体大部分变形量较小，较大变形发生在行走轴系末端的动力分配轴端盖和动力及刹车制动轴端盖附近，变形量接近0.1mm，变速箱壳体的总变形也接近0.1mm。这将影响摩擦片在X方向的自由移动，导致收割机不能正常刹车或转弯，同时可能影响变速箱内部传动轴的位置，导致齿轮不能正常啮合，影响整机的工作效率。

图12为变速箱壳体的应力分布云图。图12中，最大应力142.95MPa，发生在壳体F处端盖孔附近。按照传统的安全因素校法,安全因数ns=1.2～2.5，其许用应力为

(13)

ZL106铝合金的抗拉强度σs=255MPa，安全系数取2，则许用应力为127.5MPa，壳体的最大应力已经超过了许用应力，壳体强度不满足要求。

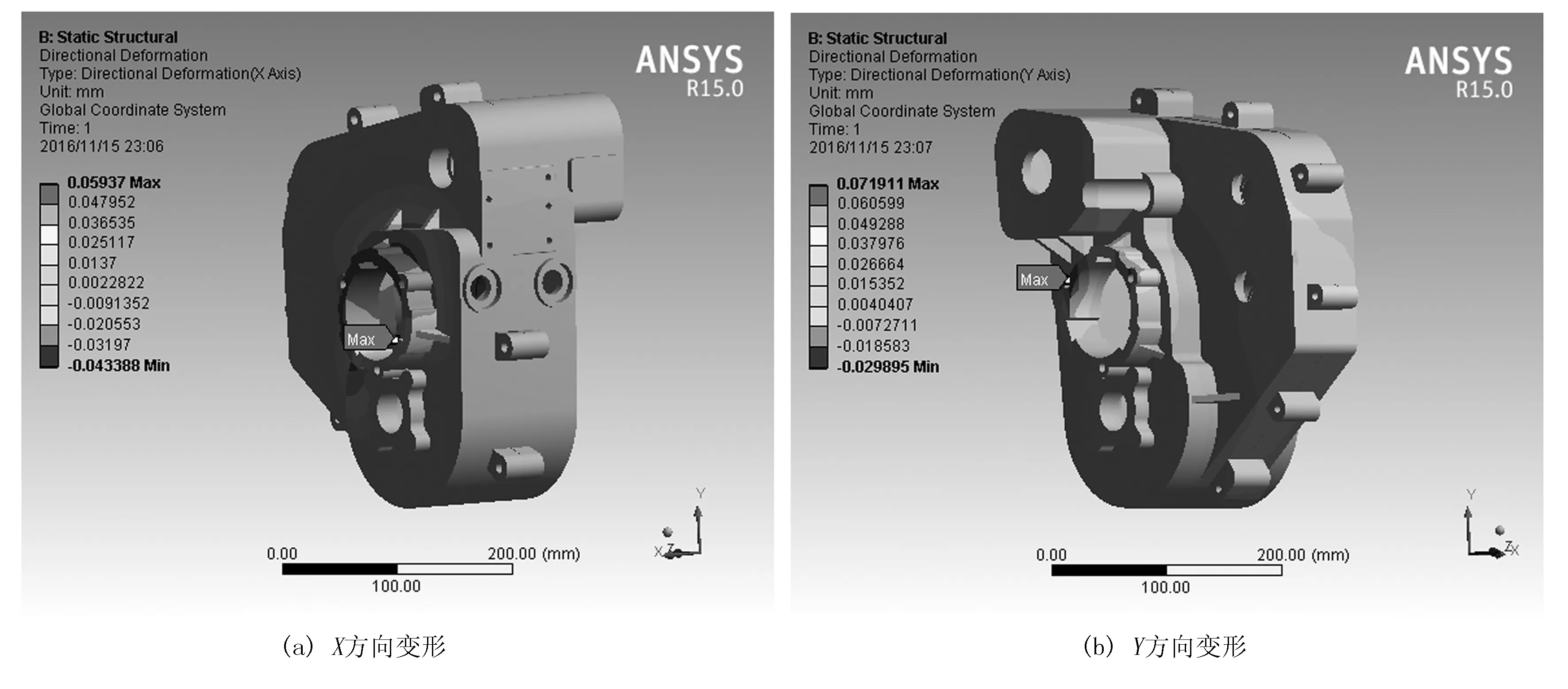
图11　优化前壳体变形

图12　优化前壳体应力

用同样的流程对壳体施加相同的约束和载荷，对优化后的变速箱壳体进行静力学分析，得到优化后变速箱壳体的变形结果(见图13)和应力结果(见图14)。图13中，优化后壳体X方向最大变形量0.031 142mm，相比改进前降低了46.2%；优化后壳体Y方向最大变形量为0.352 79mm，相比优化前降低了50.9%；优化后壳体Z方向最大变形量为0.022 462mm，相比优化前降低了47.4%，优化后壳体的总变形最大值0.047 234mm，相比优化前降低了49.1%。优化壳体的变形结果说明壳体的最大变形还是出现在F处的端盖孔上。图14中，优化后壳体应力分布得到改善，应力最大值为68.343MPa，相比优化前降低了52.2%，比许用应127.5MPa小，满足壳体强度要求。以上对比分析证明：优化设计后壳体的变形减小，F处端盖孔的变形及总变形的最大值不足0.05mm，且应力分布更加合理，强度和刚度有明显提高。同时，优化后变速箱壳体质量为8.619 1kg，比优化前的10.396kg降低了17.1%，性能得到提高，且减轻了质量。

图13　优化后壳体变形Fig.13　Shell deformation after optimization

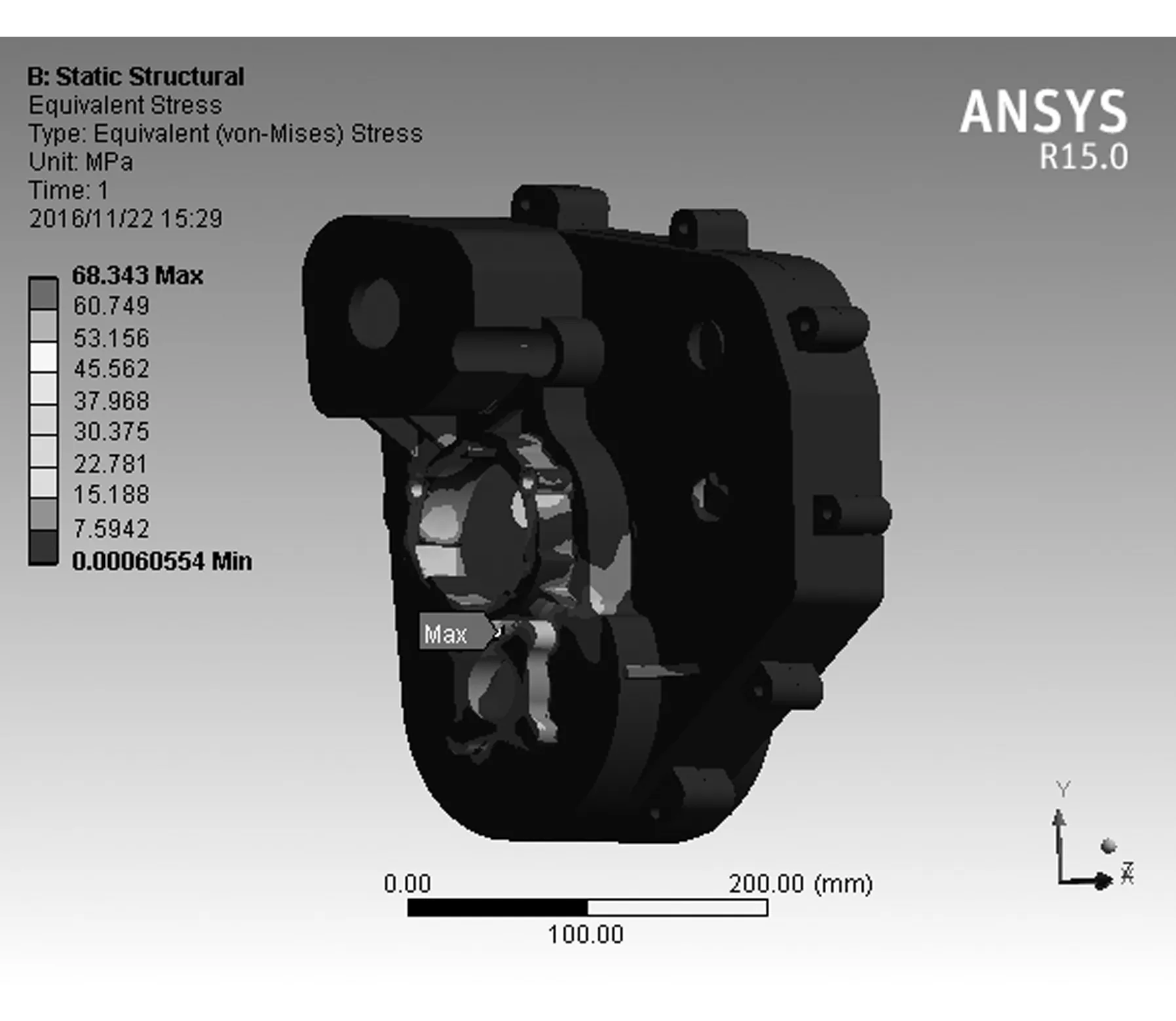
图14　优化后壳体应力Fig.14　Shell stress after optimization

5　结论

1)通过变密度法的拓扑优化方法，对变速箱壳体进行拓扑优化设计，可去除部分多余材料，并得到加筋的最佳布局，很好地控制了结构的总质量。

2)通过建立变速箱壳体结构尺寸优化模型，对影响变速箱壳体强度、刚度较大的尺寸进行基于响应面的尺寸优化，通过多目标优化得到尺寸参数的最优解，壳体结构达到最优布局。

3)通过对变速箱壳体优化前后对比分析可知：在满足刚度、强度的前提下，结构最终设计总质量控制在8.6191kg，减少17.1%，壳体的结构更合理，变形减小，应力分布更加合理，实现了轻量化设计。

参考文献：

[1]李金龙,吴超,廖敏.拔叉零件的结构设计及改进[J].机械设计与制造,2016(5):30-34.

[2]陈玲,刘静,曾山.便携式多功能收割机在丘陵山地的示范与应用[J].农机化研究, 2012,34(10):246-249.

[3]李耀明,邓玲黎,丁为民.小型联合收割机清选装置的技术分析[J].农机化研究, 2004(3):55-56.

[4]徐立友,曹青梅,周志立,等.拖拉机变速箱发展综述[J]. 农机化研究, 2009,31(12):189-192.

[5]易军,廖敏,王强,等.收获机变速器箱体静力学分析与结构改进[J].中国农机化,2016(6):18-22.

[6]鄢敏丽. 基于拓扑优化方法的专用齿轮箱轻量化研究[D]. 重庆:重庆理工大学, 2014.

[7]朱剑峰,林逸,陈潇凯,等.汽车变速箱壳体结构拓扑优化设计[J].吉林大学学报:工学版, 2013(3):584-589.

[8]阳志光,陈敏, 隋允康. 响应面法在圆柱壳体结构优化设计中的应用[J]. 弹箭与制导学报, 2007(3):127-130.

[9]王延克. 基于响应面法的汽车悬架系统优化设计[D].成都：西南交通大学, 2009.

[10]孙涛,张妙仙,李苗苗，等. 基于对应分析法和综合污染指数法的水质评价[J]. 环境科学与技术,2014(4):185-190.