基于PC-crash的直接线性变换法车速误差修正模型
何 烈 云
(浙江警察学院 交通管理工程系,杭州 310053)
0 引 言
随着CCD图像传感器技术成熟和制作工艺的提升,当前使用的非量测数码摄像机的感光芯片采用的是CCD图像传感器[1]。CCD摄像机可直接获得数字影像并输入计算机进行处理,建立摄像机图像中的点与空间物体表面点相互之间的对应关系,这一过程称为摄像机标定[2]。Abdel-Aziz等在上世纪70年代提出直接线性变换(Direct Linear Transformation,DLT)法,不需要内、外方位元素,可直接建立二维像片影像坐标和相应物点物方空间坐标之间几何关系,非常适用于非量测CCD摄像机的标定[3]。运用DLT,再现交通事故中目标车辆运行轨迹和车速等数据,是实现交通事故现场信息重构的一种有效途径[4]。DLT测算交通事故中目标车辆的行驶速度与传统的目标车辆参照物法、道路环境参照物法、虚拟参照物法相比[5-7],具有灵活方便、受时空影响小及具备描绘目标车辆空间轨迹的功能。但在实践中发现,DLT测算目标车辆行驶速度精度没有优势,若坐标标定点和目标车辆特征点选取不当,行驶速度测算精度不高[8-11]。
随着数码技术的发展,数码摄像设备成像质量不断提升,因摄像头成像质量引起的误差也越来越小,对近景摄影中目标车辆车速影响基本可以忽略。矩阵实验室—Matlab(Matrix Laboratory)软件在矩阵运算方面强大的功能,因算法对DLT精度影响也可忽略不计。实践表明,影响DLT车速测算误差:① 由于人为的测量误差引起的偶然误差,即物方坐标系中点测量误差、像方坐标系点像素坐标测量误差,这类误差是无法避免的,在实践中可以进行多次测量求平均值方法提高精度;② 由于目标车辆不同特征点测算速度与车辆行驶速度差异引起的误差,这类误差属于系统误差,误差值具有一定的单向性[12]。本文对DLT车速测算系统误差形成的机理进行了分析、提出了修正系数模型,并运用仿真实验,对系统误差修正系数模型的可行性进行了验证。
1 系统误差修正模型构建
摄像机成像实质是根据透镜成像原理,把三维空间投影到二维像平面的过程,人们可以借助二维像素坐标点(x,y)获取三维空间坐标点(X,Y,Z)相关信息[13]。为了方便车辆特点选取而引起的误差分析,将汽车简化成与xOy平面垂直的杆子模型,构建如图1所示的分析图。



(1)

[(y1+Δy1)-(y2+Δy2)]2}1/2
(2)
假设摄像头光心距离地面的高度为H;杆子的高度为h,则:
结合式(1)、(2)可知:
s′=Hs/(H-h)
(3)
令修正系数:
k=H/(H-h)
由式(3)可知,选取杆子上下2个不同端点为特征点时,车辆实际行驶速度v与DLT测算车速v′满足关系:
v=v′/k
(4)
当摄像头固定,系数k大小取决于特征点离地面的高度h。
由于在摄像机标定时坐标测量误差、摄像机畸变、计算时数值近似等因素引起的误差,用相对误差ε表示,这种误差会对所有测算车速造成单向的影响,可以视为系统误差。在实验数据处理时可以使用该相对误差值对测算车速进行补偿,提高精度。综合以上公式,得到误差修正模型表达式:

(5)
2 PC-crash仿真实验验证
为了验证式(5)误差修正模型的是否可行,在实车DLT车速测算实验中,由于实验结果受到道路的线形、实验用车速度稳定性、驾驶员操控水平、车辆测速仪的精度、摄像机拍摄操作、人为测量误差等变量共同的影响,难以对单一变量的影响做出定量及定性的分析。为有效克服这些缺点和不足,可采用仿真实验的方法。
2.1 仿真实验
仿真实验不受时间、空间限制[14],完全排除实验过程中的过失误差,尽量减少偶然误差。而且在实验过程中方便控制某些变量,对单一变量变化对结果的影响进行研究分析,这是实车实验无法实现的。运用PC-crash软件[15]开展DLT车速测算仿真实验时,① 利用软件自带的道路模型工具建立理想的道路模型,灵活地在道路上施划交通标线,设置交通标志和其他的道路环境参照物体;② 根据对比实验需要对导入的设置车辆外观尺寸参数、调整车辆行驶状态进行设置;③ 灵活设置摄像机的分辨率、位置、焦距及相机倾角等实验参数。PC-crash软件道路、车辆和摄像机重要参数设置窗口如图2所示。

图2 实验参数设置窗口
2.2 实验设计
实验时构建一条双向6车道平直道路,每条车道宽度为3.5 m;道路上施划车行道分界线、白色车道分界线的线段及间隔长度分别为60 cm和90 cm;斑马线长度、宽度及相邻间隔分别为6 m、40 cm和1 m;道路两旁的灯柱间距12 m。实验车辆选择PC-crash车库模型中的丰田卡罗拉(Toyota corolla)车型,车子的长宽高为4 630 mm×1 775 mm×1 485 mm。实验时设置车辆以60 km/h速度作匀速直线运动;摄相机离地高度5 m,相机倾角铅直方向为-11.6°、水平方向为-152.3°。在PC-crash中生成并导出仿真视频,设置视频帧频率为25帧/s、视频图像分辨率为1 360×768,图3为仿真实验视频截图。

图3 仿真实验视频截图
图3中B1~B4为4个坐标标定点;T1~T4为实验车辆选取的4个待测的特征点,其中点T1为左前轮与地面接触点,T2为左后轮与地面接触点,T3为车前头车标中心点,T4为左后视镜中间点;J1~J6路边灯柱底座的相机标定偶然误补偿点,相邻两点间距恰为灯柱间距12 m。以B1点为坐标原点,B1B2和B1B4为坐标轴建立物方坐标和像方坐标,各标定点物方坐标和像方坐标如表1所示。将表1数据代入式(2),运用Matlab程序计算得出虚拟相机li8个参数值,分别为:
l1=-0.132 548 386 111 6
l2=-0.069 943 246 558 9
l3=-0.000 457 189 161 4
l4=-0.469 197 827
l5=0.611 631 368 845 054
l6=-0.027 843 792 367 3
l7=227.672 380 551 601
l8=-196.053 896


表1 标定点坐标值

表2 摄像机标定相对误差
以车辆T1~T4为4个特征点,截取相互间隔20帧的4个关键帧F1~F4,如图4所示。
测算车辆相邻关键帧特征点平均速度v1~v4结果如表3所示。
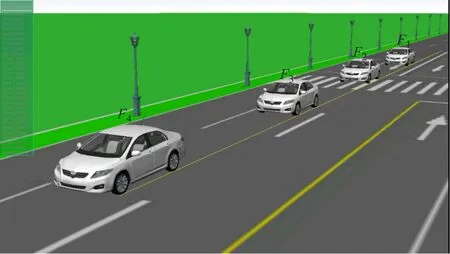
图4 仿真实验视频图像叠加效果图

关键帧特征点DLT测算速度/(km·h-1)v1v2v3v4F1~F261.461.371.376.3F2~F361.161.471.976.9F3~F461.361.670.676.2测算速度v61.361.471.376.5相对误差,ε/%1.01.318.827.5
3 仿真实验验证结论
分析表3中实验数据,可得到以下结论:
(1) 车速测算值误差值与目标车辆所处区域无直接关系,在选取关键帧时,只要确保特征点处在视频图像明视范围即可;数据还表明在摄像机标定时,摄像机参数精度不受标定点所围区域、相机倾斜角影响。
(2)T1、T2测算速度和车辆实际行驶速度相对误差只有1.0%左右,该误差主要是由于测量特征点的像方坐标测量时人为因素造成。
(3)T3、T4测算速度比车辆实际行驶速度大,而且特征点距地面高度差越大,速度差越大。
根据丰田卡罗拉(Toyota corolla)车型外观、实验参数设计值,将表3补偿后车速运用修正模型(5)进行修正,结果如表4所示。

表4 修正车速和相对误差
通过仿真实验表明,车辆不同特征点DLT测算车速度有差异,但对结果进行修正后不同特征点速度与实际车速度非常接近,验证了修正模型正确性和现实可行性。
4 结 语
DLT在再现交通事故中目标车辆的行驶速度时,会因车身特征点选取不当而造成车速测算误差较大。理论分析和仿真实验表明,在DLT车速测算时,可以通过测算目标车辆车身其他任一点的速度,运用修正系数对该点测算速度进行修正,进而得到目标车辆的行驶速度。引入修正系数模型,可以大大提高了DLT车速测算的精度和灵活度,为夜间目标车辆车速精确测算提供了理论依据和操作方法。在实践中,可以运用修正系数模型中各变量之间关系,推测出摄像机的安装高度、成像物体上任一点空间高度。
参考文献(References):
[1]王晓涛,王绪安,康宁. CCD摄像机新型光控技术研究[J]. 红外与激光工程,2016,45(1):0120003-1-0120003-6.
[2]赵高长,武风波,周彬,等. 基于DLT模型的摄像机标定简化方法[J]. 应用光学,2009,30(4):585-589.
[3]鲁光泉,李一兵.基于普通数码相机的交通事故摄影测量技术及其研究进展[J].交通运输工程与信息学报,2005(3): 63-67.
[4]陆玉凯,金先龙,侯心一. 数字摄影测量技术在交通事故再现中的应用[J].计算机辅助设计与图形学学报,2005,17(10): 2318-2322.
[5]何烈云.基于视频处理技术车辆定位法的研究[J].武汉理工大学(交通科学与工程版),2014,38(2):469-471.
[6]靳慧云,李苑,谢贤能,等.监控视频中目标车辆速度被动式测量方法研究[J].测绘通报,2012(8):47-50.
[7]何烈云.帧间差分法车速测算技术误差分析与处理[J].中国人民公安大学学报(自然科学版),2014(1):56-59.
[8]曾友,高健,岑誉.视觉技术的中心定位误差方法研究[J]计算机仿真,2015,32(7):264-267.
[9]严韶华,陈道清,郭平波. DLT直接解法与迭代解法的讨论[J].工程勘查,1989(5):68-70.
[10]邹峥嵘. 坐标差DLT与DLT解法的比较[J].四川测绘,1995,19(2):59-60.
[11]杜召彬,邹向东. 基于灭点的透视校正和空间定位的方法研究[J]. 四川理工学院学报(自然科学版),2011,24(1):105-108.
[12]陈涛,丁星兵,何仲华,等. 基于视频建立的车速分析数学模型的误差研究[J].公路交通科技(应用技术版),2015(7):254-256.
[13]韩学源,金先龙,张晓云,等. 基于视频图像与直接线性变换理论的车辆运动信息重构[J].汽车工程,2012,34(12):1145-1149.
[14]易红.高校实验教学与创新人才培养[J].实验室研究与探索,2008(2):1-4.
[15]何烈云.基于PC-Crash软件侧翻交通事故再现实验方法研究[J].实验技术与管理,2015,32(12):135-139.

