压缩感知中一种改进的迭代硬阈值算法
李 佳,刘献杰,智世鹏
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
0 引言
压缩感知(Compressive Sensing,CS)指出,只要信号本身或在某个变换域上是稀疏的,就可以用一个与变换矩阵不相关的测量矩阵将变换域的高维信号投影到一个低维空间上,并通过求解一个优化问题把原信号以高的概率重构出来[1-3]。压缩感知理论的主要内容包括信号稀疏表示、测量矩阵构造[4-7]以及重构算法设计[8],其应用已扩展到无线传感网络[9]、信道估计[10]等众多应用领域。
自CS理论提出以来,涌现了大量重构算法,这些算法主要分为两类:一类是基于最小化l1范数的线性规划方法,包括BP算法[11]、内点法等;另一类是基于最小化l0范数的贪婪算法,包括OMP算法[12]、ROMP算法[13]、SP算法[14]以及有良好重构性能的IHT算法[15]、NIHT算法[16]、BIHT算法[17]等。虽然线性规划方法能够得到较高的重构精度,但是其高计算复杂度极大地限制了应用。贪婪迭代算法以其迭代快速而获得广泛应用,但是其重构的性能有待提高。
在原始IHT算法的基础上,BIHT算法在每次迭代过程中加入了回溯过程,并采用基于最小二乘法的伪逆运算来获取原始稀疏信号的估计值。上述两个改进方式大大地提高了重构性能,尤其是传承了贪婪算法精髓的伪逆运算。然而,BIHT算法在每次迭代过程中的回溯操作相对简单,仅仅是将前一次迭代过程中的支撑集合并。
基于最小二乘法的稀疏信号重构中重构误差为理论基础,通过理论分析重构误差的显示表示,并将保证重构误差随算法迭代逐步较小的理念融入到回溯过程,设计一类改进的迭代硬阈值算法。该算法在每次迭代过程中基于重构误差的差值选择合并的指标,并利用基于最小二乘法的伪逆运算来获取原始稀疏信号的估计值。通过高斯稀疏信号和0-1稀疏信号的重构仿真实验验证了本文所提算法在重构效率和重构性能方面的优势。
1 压缩感知理论
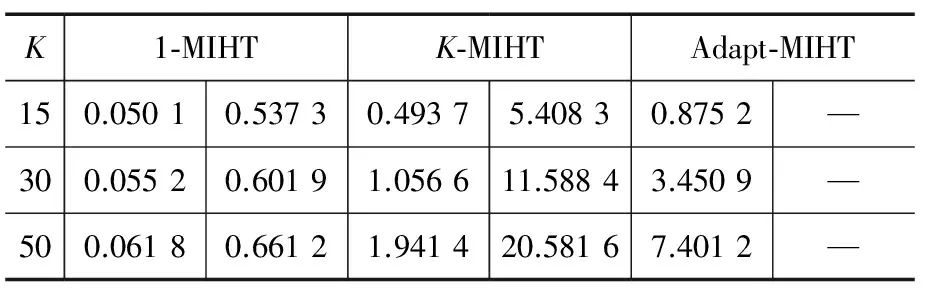
对于任意N维信号x={x1,...,xN}∈RN,支撑集supp(x)表示x的非零坐标。当|supp(x)|=K< min‖x‖0使得y=Φx。 (1) 求解上述优化问题是一个NP问题。为保证稀疏信号的精确重构,测量矩阵Φ应满足下述有限紧致特性(RIP)[2]。 定义1:原始信号支撑集supp(x)=T⊂{1,...,N},矩阵ΦT由列数i∈T的列向量构成,任意矢量q∈R|T|,K (2) 则称Φ满足参数(K,δ)的有限紧支特性(RIP),其中0≤δ≤1,∀|T|≤K,∀q∈R|T|。 文献[15]为迭代硬阈值(IHT)算法用于压缩感知重构信号提供了一系列的理论保证,证明算法成功运用较少的测量向量逼近原始信号,其迭代过程如下:假设x0=0,迭代 xn+1=HK(xn+ΦT(y-Φxn)), (3) 式中,HK(α)是一个非线性算子,保留向量α中绝对值最大的K个分量,其他分量均设为零。如果按这样的机制获得非零支撑集合不唯一,则可随机选择其中一个集合或者预设要选择分量的支撑集合。 上述算法更一般的形式是包含额外的步长μ>0,即 xn+1=HK(xn+μΦT(y-Φxn))。 (4) 运用式(4)进行迭代。Blumensath等人在文献[16]中对上述迭代过程做了改进,通过在迭代中加入一个自适应决定的下降序列因子{μn}来保证算法的收敛及重构的实现,使得算法保持尺度独立。 文献[17]提出了一种基于回溯的迭代硬阈值算法(BIHT),该算法在每一次迭代过程中增加一步回溯的思想,前次迭代结果与非线性算法HK(α)产生的新向量支撑集合并,再通过伪逆过程与非线性算子HK(α)重新得到信号的逼近解。BIHT算法重构信号仅仅需要很少的迭代次数即可高概率重构原始稀疏信号。 通过分析文献[17]中的BIHT算法可知,利用估计支撑集Λn或者Γn得到的重构效果没有定量的评价,即无法保证支撑集Λn对应的重构误差一定小于支撑集Λn-1对应的重构误差,本文提出的改进的迭代硬阈值算法就是针对上述不确定问题提出的,即可保证重构误差随迭代的进行而逐渐减小。 给定稀疏信号x,若估计支撑集为Λn,则重构误差可表示为: (5) 其中,I=|Λn|=K。对任意i∉Λn,若Γn=Λn∪{i},则重构误差的差值为[18-19]: (6) 然而,当并入的指标多于1个时,无法得到上述理论保证。最理想的方式是初始化并入支撑集的原子数等于信号的稀疏度K,当在某次迭代过程中无法保证RΓn-RΓn-1≤0成立时,放弃此次支撑集合并,改用K-1个指标进行支撑集更新,以此类推直到条件RΓn-RΓn-1≤0满足成立。从理论上,此不同于BIHT和SP的回溯过程可保证稀疏信号的重构误差随着迭代次数的增加而减小,即以稀疏优化问题的全局最优解为最终目标。本文记基于上述支撑集更新的稀疏信号重建算法为Adaptive-MIHT算法。 由上述理论分析可知,此类稀疏重构算法的计算复杂度集中于指标的选择以及基于最小二乘法的伪逆运算这两个过程。Adaptive-MIHT算法从理论上可以保证每次迭代过程中支撑集的选择是最优的,但是其自适应选择不同数据的支撑指标过程给计算复杂度带来了极大的不确定性,因为其会从K开始进行遍历选择能够保证重构误差单调减小的指标数目。虽然上述过程能够为迭代次数的减小带来可观的增量,但是其在算法重构后期会因为数量较少的指标导致在每次迭代过程中花费较长的时间完成指标自适应选择,这给稀疏信号重构效率带来了极大的挑战。 为了验证此类算法进行稀疏信号重构的统计性能,本文在仿真实验部分采用基于蒙特卡洛的方法,以并入1个和K个原子为例,并分别命名2种算法为1-MIHT和K-MIHT算法。由上文可知,1-MIHT算法是K-MIHT算法中K=1的特殊情况。出于文章篇幅的考虑,本文仅以K-MIHT算法为例进行算法的详细介绍。 K⁃MIHT算法输入值:测量值y,测量矩阵Φ,稀疏度K;初始化:x1=0,n=1,r1=y,步长=K;迭代:在第n次迭代中执行下述步骤,直到满足终止条件1:αn=HK(xn+ΦT(y-Φxn)),Λn=supp(αn);2:ζ=ΦTy,Ψ=ΦTΦ;3:χ[Λn,:]=(ΦΛnTΦΛn)-1ΦΛnTΦ,Γn=Λn;4:forj=1:Ki^=argmaxi∈{1,...,N}Γn(ζi{}-ζΓnTχ[Γn,i])2Ψ[i,i]-Ψ[Γn,i]Tχ[Γn,i]w=χ[Γn,i^TΦΓnT,v=wΦ-Ψ[i^,:]Ψ[i^,i^]-Ψ[Γn,i^]Tχ[Γn,i^]χ[Γn,:]=χ[Γn,:]+χ[Γn,i^]vχ[i^,:]=-v,Γn=Γn∪{i^} end5:x~n+1=Φ†Γny,xn+1=HK(x~n+1)输出值:重构稀疏信号x^。 本节以重构一维高斯稀疏信号和0-1稀疏信号为例,详细验证本文所提的Adaptive-MIHT、1-MIHT和K-MIHT算法在稀疏信号重构方面的性能。 首先进行稀疏信号重构时间的比较,仿真实验运用在CPU 为Intel E7500(双核2.93 GHz),内存为4 GBd的联想机上。选取长度为N=256的0-1稀疏信号,其非零元素值为1,稀疏度K分别取15、30、50。测量矩阵选取128×256高斯随机矩阵。每个算法分别运行10次和100次迭代,且重复运行100次稀疏信号重构,得到下述平均重构时间,如表1所示。由表1可知,当迭代次数为10且稀疏度K较小时,3种算法的重构时间相当,且随着稀疏度增大,Adaptive-MIHT算法变得越来越慢。特别的,当迭代次数为100时,Adaptive-MIHT的重构时间超过10 min,表现出极不理想的重构效率。 表1不同算法重构时间比较 K1⁃MIHTK⁃MIHTAdapt⁃MIHT150.05010.53730.49375.40830.8752—300.05520.60191.056611.58843.4509—500.06180.66121.941420.58167.4012— “—”表示运行时间超过10 min。 其次,采用蒙特卡洛方法进行算法重构性能的比较。考虑到Adaptive-MIHT算法在重构效率方面的劣势,本实验仅验证K-MIHT算法和1-MIHT算法,并选取IHT算法、NIHT算法以及BIHT算法为参考算法。选取长度为N=256的高斯随机稀疏信号和0-1稀疏信号,其中高斯随机稀疏信号的非零元素值满足N(0,1)分布,而0-1稀疏信号的非零元素值为1。测量矩阵选取128×256高斯随机矩阵。 图1 重构算法性能比较图(高斯稀疏信号) 从图1可以看出1-MIHT和K-MIHT算法重构一维高斯稀疏信号性能明显高于IHT算法、NIHT算法以及BIHT算法。特别的,当稀疏度<53时,K-MIHT算法的精确重构概率接近1,但是当稀疏度继续增大时精确重构概率急剧降低。经分析,导致上述重构性能急剧下降的原因应该是算法迭代过程中回溯步骤固定地选取了K个原子并入支撑集,并未得到局部最优解。 图2 重构算法性能比较图(0-1稀疏信号) 从图2可以看出,1-MIHT和K-MIHT算法重构0-1稀疏信号性能亦明显高于IHT算法、NIHT算法以及BIHT算法。值得注意的是,K-MIHT表现出了非常好的性能,体现了IHT类算法中非线性算子HK(α)重构0-1稀疏信号的高效性。 随着压缩感知中贪婪类稀疏重构算法研究的深入,在算法迭代过程中加入回溯操作成为非常受关注的方向。本文基于IHT算法提出了一种与BIHT算法不同的回溯操作,该操作通过保证重构误差逐渐减小能够提供非常优秀的重构性能。从一维稀疏信号重构实验来看,相比IHT、NIHT和BIHT算法,本文所提算法重构性能是最优的。然而,如何在Adaptive-MIHT算法的每次回溯过程中快速准确地选择最优数量的原子来扩展估计支撑集仍然是值得后续研究的问题。 [1]Donoho D L.Compressed Sensing[J].IEEE Transaction on Information Theory,2006,52(4):5406-5425. [2]Donoho D L,Tsaig Y.Extensions of Compressed Sensing [J].Signal Processing,2006,86(3):533-548. [3]罗纯哲,陈金杰,王蔚东.压缩感知理论与非凸优化方法研究[J].无线电工程,2014,44(5):20-29. [4]王强,李佳,沈毅.压缩感知中确定性测量矩阵构造算法综述[J].电子学报,2013,41(10):2014-2050. [5]李佳,王强,沈毅,等.压缩感知中测量矩阵与重建算法的协同构造[J].电子学报,2013,41(1):29-34. [6]王戈,王辉,王小强,等.基于交替投影的多参数联合解调算法[J].无线电工程,2016,46(9):37-40. [7]张业,李佳.一种压缩感知词典快速构造方法[J].无线电通信技术,2017,43(3):30-33. [8]何国栋,谢小娟,杨凌云,等.基于压缩感知的信号重构研究[J].无线电通信技术,2014,40(3):26-28. [9]刘晓彤.基于DCS的无线传感网络数据压缩算法研究[J].无线电通信技术,2017,43(1):23-26. [10] 杨剑,蒋挺,赵成林,等.基于CS-ROMP算法的超宽带信道估计[J].无线电工程,2011,41(5):14-17. [11] Chen S B,Donoho D L,Saunders M A.Atomic Decomposition by Basis Pursuit[J].SIAM Journal on Scientific Computing,1998,20(1):33-61. [12] Davenport M A ,Wakin M B.Analysis of Orthogonal Matching Pursuit Using the Restricted Isometry Property [J].IEEE Transaction on Information Theory,2010,56(9),4395-4401. [13] Needell D,Vershynin R.Signal Recovery From Incomplete and Inaccurate Measurement Via Regularized Orthogonal Matching Pursuit[J].IEEE Journal of Selected Topics in Signal Processing,2010,4(2):310-316. [14] Dai W,Milenkovic O.Subspace Pursuit for Compressive Sensing Signal [J].IEEE Transaction on Information Theory,2009,55(5): 325-330. [15] Blumensath T,Davies M.Iterative Hard Thresholding for Compressed Sensing [J].Appl.Comput.Harmon.Anal,2009,27:265-274. [16] Blumensath T,Davies M.Normalized Iterative Hard Thresholding:Guaranteed Stability and Performance[J].IEEE Journal of Selected Topics in Signal Processing,2010,4(2):298-308. [17] 杨海蓉,方红,张成,等.基于回溯的迭代硬阈值算法[J].自动化学报,2010,37(3): 276-282. [18] 史荣昌,魏丰.矩阵分析[M].北京:北京理工大学出版社,2005. [19] Varadarajan B,Khudanpur S,Tran T D.Stepwise Optimal Subspace Pursuit for Improving Sparse Recovery [J].IEEE Signal Processing Letter,2011,18(1): 27-30.2 迭代硬阈值算法
3 改进的迭代硬阈值算法
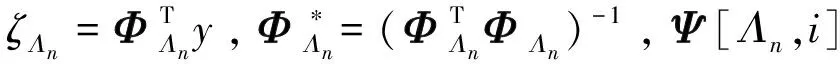

4 仿真实验
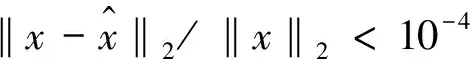


5 结束语

