考虑执行器故障的电动汽车空调鲁棒控制

胡广地,王国晖,罗慧玉,周　柯,郎晓玥

(1.西南交通大学机械工程学院,四川 成都 610031; 2.西南交通大学土木工程学院,四川 成都 610031)

电动汽车空调系统作为电动汽车最主要的电动化附件之一,其性能的好坏直接影响电动汽车的续航里程和乘客乘坐的舒适性.目前,针对电动汽车空调控制系统的研究很多,主要基于传统控制、智能控制和鲁棒控制理论.传统控制主要包括开关控制、PID控制等.早期Jette等采用开关控制方式对蒸发器出口过热度进行控制[1]，这种控制方式简单,但是控制精度很低,容易造成执行器件损坏.Wei等采用PID控制方式对电子膨胀阀和压缩机的动作进行调节[2]，这种控制方式控制精度更好,但未能充分利用空调系统内部信息,在外部干扰较大时，不能达到理想的控制效果.智能控制在空调制冷系统中的应用主要为神经网络控制[3-4]，是典型的黑箱建模技术,无需对系统物理意义了解过多,但需要大量的数据才能得到较为精确的数学模型,故市场接受度较低.鲁棒控制主要包含有鲁棒控制、滑模控制等，Zhang等在汽车空调这一领域的研究较多,对相应的控制指标控制效果较好[5-6].

针对汽车空调系统的故障检测与控制也已成为国内外一个重要的研究方向.早期的空调故障依赖于简化模型,这类模型对于空调工况瞬态变化存在严重的模型失真[7].任春晖等以故障树模型研究方法为基础,对汽车空调在运行过程中的制冷剂不足等问题进行了研究[8]，但其研究主要集中在空调系统的故障诊断,对于系统在出错状态下的容错控制并未做过多探讨.国外在汽车空调故障诊断和隔离的研究较多，目前多采用基于观测器的观测法和频域分析法，其中，在观测器法中,采用H∞滤波器可有效的抑制由系统不确定性和外部干扰所带来的影响.Zhang等针对执行器中的压缩机故障、传感器故障以及参数失真等问题建立了空调系统故障模型,并建立了该模型的输出反馈控制器[9]，但在执行器故障模型中未考虑膨胀阀以及循环风门发生故障时对系统带来的影响.本文提出了一种基于执行器故障模型的电动汽车空调系统控制方法，将汽车空调执行器故障按照失效、中断和偏移等进行分类,在控制器设计中充分考虑上述故障形式,保证系统在部分故障的条件下，依然满足空调系统性能要求正常工作.

1　电动汽车空调系统数学模型

电动汽车空调系统组成主要由涡旋式压缩机、冷凝器、膨胀阀和蒸发器组成[10-11]，如图1所示.

由于电动汽车车厢仅与蒸发器出口状态参数关系密切,故本文中仅考虑压缩机、膨胀阀、蒸发器,建立相对应的状态空间方程，不考虑相邻相区之间的制冷剂质量流量之间的损耗,得到只包含蒸发器电动汽车空调制冷循环的方程为

(1)

定义：压缩机输出转速为Nc；膨胀阀开度为α；循环风门开度的系统输入为αin，则有u=(Nc，α，αin)T.换热模型的详细描述见文献[13].

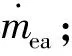
定义：系统输出为蒸发器压力为pe；过热度为SH；蒸发器出口处空气温度为Tea,out；相对湿度为ωea,out，则有y=(pe，SH，Tea,out，ωea,out)T.

图1　电动汽车空调系统模型Fig.1　Electric vehicle air conditioning system model

为了便于进行控制器设计,将式(1)在空调的工作点附近进行局部线性化处理.其中，最主要是需对Ze(xe)进行线性化处理[14].选择系统的工作点(xe,ue,we)，其中：根据文献[5]中Ze(xe)的格式，可知在其工作点Ze(xe)的满秩矩阵,进而可得动态扰动模型为

(2)

式中:δx=x-xe；δu=u-ue；δw=w-we；xe、ue、we分别为稳定状态时状态向量、控制输入和扰动.

根据系统稳态工作点(xe,ue,we),可以得到状态矩阵的偏导关系式为

(3)

记

同时，对y=g(x)在其工作点进行局部线性化处理,则可以得到线性模型为

(4)

2　汽车空调执行器故障模式分析

执行器在故障条件下，空调系统输入为[15]

uF(i,j,t)=m(i,j,t)u(i,t)

+σ(i,t)us(i),

(5)

式中:uF(i,j,t)为第i个执行器在第j种故障模式在时刻t时的被控输入;m(i,j,t)为执行器第i个执行器在第j种故障模式下的效率因子;u(i,t)为第i个执行器的被控输入;σ(i,t)为第i个执行器在第j种故障模式下偏移或卡死的常数因子;us(i)为第i个执行器偏移或卡死的被控对象常值输入.

相应的故障模式如表1所示[16].

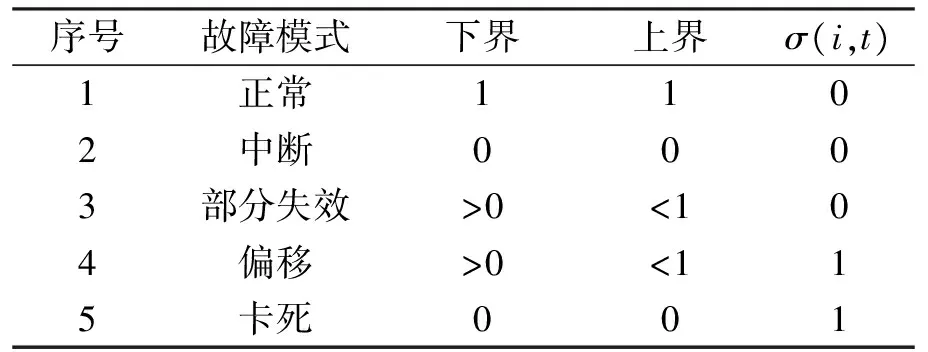
表1　故障模式Tab.1　Failure mode

对于实际的空调系统,由于膨胀阀开度以及循环风门开度最大开度均为100%,根据表1所述偏移故障的定义,这两个执行器均不可能出现开度大于100%的情况,即这两个控制器均不会出现偏移故障.为便于描述,将式(5)简写为

uF(t)=m(t)u(t)+σ(t)us.

(6)

由式(6)可知,若压缩机输出转速、膨胀阀开度以及循环风门开度中某一个或某几个发生部分失效、偏移、卡死或者中断等问题时,即可判定为执行器故障.将式(6)代入式(4)，得到包含有执行器故障模式的电动汽车制冷系统的状态方程为

(7)

本文的控制任务是对式(7)所述带有执行器故障的电动汽车空调制冷循环系统,考虑系统的扰动和执行器扰动,设计状态反馈控制律u(t),消除执行器故障和扰动对系统稳定性所带来的影响.

3　考虑执行器故障的H∞状态反馈控制器设计

3.1　状态观测器的设计

电动汽车空调制冷系统中，状态变量如两相区长度、过热区出口焓值等不能直接测得，需要对其状态进行观测.本文采用状态观测器对制冷空调系统状态变量进行观测.

构造线性化后模型(1)的开环状态观测器为

(8)

引入观测矩阵L,则状态观测方程为

(9)

定义真实状态和估计状态的误差向量为e,则有

当(Aac-LCac)的特征值有负实部时,状态向量误差按照指数衰减,即

(10)

3.2　反馈控制器的设计

将式(7)简化为

(11)

式中:

δ(t)=σ(t)urs.

由于

diag{m(1,t)-1,m(2,t)-1,m(3,t)-1}

m(i,t)∈[0,1],i=1,2,3.

针对式(7)设计状态反馈控制器为

(12)

式中:Kac为一常数矩阵,使得对于所有的故障模式,闭环系统是二次稳定的,满足

(13)

式中：yr(t)为系统输出；γ为稳定裕度系数；ωr(t)为扰动.

由于δ(t)=σ(t)us,一般地,控制器输出是有限制的,即:umin≤us≤umax,故存在常值矩阵Θ,使得

(14)

关系成立.

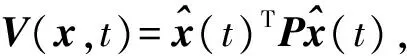
(15)

引理1[16]对于任意具有适当维数的矩阵H、F(t)、E,其中，F(t)满足FT(t)F(t)≤E,则对于任意的ε>0,有

HF(t)E+ETFT(t)HT≤

ε-1HHT+εETE.

(16)

不考虑干扰输入的作用,将式(12)代入式(11)得到闭环系统，即

(17)

类似式(17)这样的系统是二次稳定的.

(18)

定义

Q=(Aac+Bac2Kac)T+P(Aac+Bac2Kac)+

(Bac2Θ)TP+P(Bac2Θ)+

则有

(19)

即当Q<0时,则闭环系统(17)二次稳定.根据引理1,可知,对于给定的ε>0,有

(Bac2Θ)TP+P(Bac2Θ)≤

则有

Q≤Q0=(Aac+Bac2Kac)TP+P(Aac+Bac2Kac)+

(20)

若使Q<0,只需要Q0<0，则

(21)

式中:λmax(Q0)为矩阵Q0的最大特征值.

取α=-λmax(Q0),即可保证闭环系统(式(17))是二次稳定的.

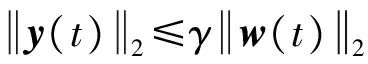
定义泛函指标

(22)

上述证明可知式(17)是二次稳定的,定义为

(23)

根据上述证明可以得到对于任意非零干扰w(t)有

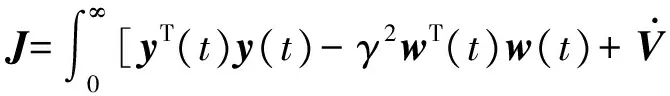
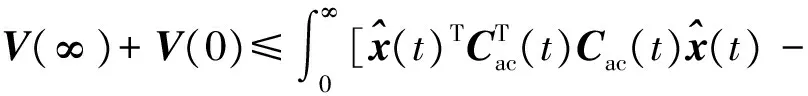
γ2wT(t)w(t)+K(x,t)]dt.

(24)

根据引理1,有

式(24)可简化为

(25)

当T<0,可保证y(t)满足H∞性能约束.

进一步利用Schur补原理，并取

Z=KacP-1，

X=P-1.

可将T<0等价为LMI问题，有

(26)

故若存在正定对称矩阵X和矩阵Z使得上述线性矩阵不等式成立,求得的控制器增益Kac=ZX-1,使得系统不仅二次稳定,而且满足H∞的性能要求.所求得的状态反馈控制器为

(27)

式(27)即为该系统考虑系统扰动和执行器故障的状态反馈输出控制器.

4　仿真对比分析

电动汽车空调系统各状态参数稳态工作点如表2所示[5].

表2　各状态的稳态工作点Tab.2　Static working point of each state

通过对模型进行线性化处理,得到电动汽车空调制冷循环方程为

通过极点配置的方法对该系统进行状态观测器的设计,所得到的状态观测器观测矩阵为

通过采用LMI对模型进行仿真,得到控制器

为不失一般性,本文对一般故障模式进行仿真实验.即第1个控制器输出偏移,第2个控制器部分失效,第3个控制器输出卡死,且在卡死状态控制器输出为控制器输出最大值.

4.1　输入干扰抑制能力分析

分别对原系统、采用一般H∞鲁棒控制原理所设计的控制器、考虑执行器故障时所设计的H∞鲁棒控制器的幅频特性进行分析.

对于幅频特性曲线,当其幅值大于0时,对输入端所产生的干扰并无抑制效果,当其幅值小于0时,其幅值越小,对输入端所产生干扰的抑制能力就越好.图2为各系统3个输入对各个输出的幅频特性曲线.由于汽车空调系统变化相对较慢,在这里主要考虑其低频段和中频段的性能.

(a)车厢进风口温度(b)车厢进风口含湿量(c)蒸发器出口压力(d)过热度注：直线黑线、红线、绿线分别为原系统各输出对3个输入频域分析；虚线黑线、红线、绿线分别为H∞闭环系统各个输出对3个输入频域分析；点线黑线、红线、绿线分别为考虑故障模型H∞闭环系统各个输出对3个输入频域分析．图2　各系统3个输入对各个输出的幅频特性曲线Fig．2　Amplitudefrequencycharacteristiccurveforeachsystemof3inputforeachoutput

由图2可知,在低频段和中频段,在多数情况下，采用容错H∞鲁棒控制器闭环系统的幅值小于采用鲁棒控制的闭环系统,且均优于原系统.这表明,容错H∞鲁棒控制器对输入端的干扰抑制能力更强.

4.2　仿真结果分析

由图3的仿真结果可以看出,基于状态观测器的容错控制器在有故障条件和无故障条件下，各个输出的相对误差很小,可以满足系统对观测误差性能的要求.

本文式的故障结构为

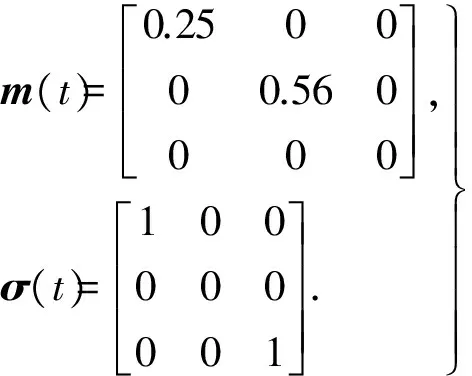
(28)

对式(28)的仿真结果如图4所示.此时，采用一般H∞鲁棒控制方法所设计的控制器在各个输出，无论是响应速度，还是超调量，均不及考虑执行器故障时的H∞鲁棒控制闭环系统稳定.

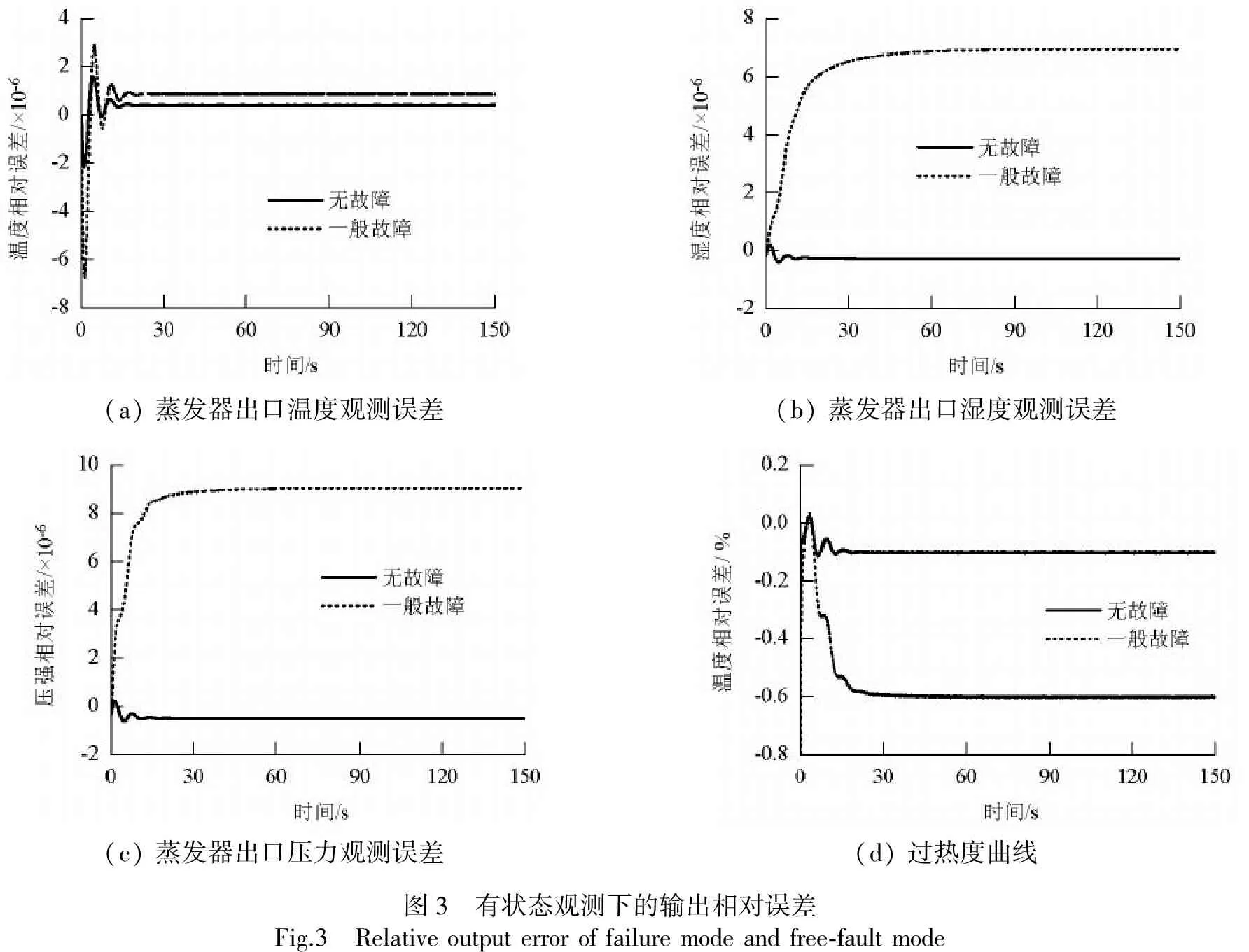
(a)蒸发器出口温度观测误差(b)蒸发器出口湿度观测误差(c)蒸发器出口压力观测误差(d)过热度曲线图3　有状态观测下的输出相对误差Fig．3　Relativeoutputerroroffailuremodeandfree⁃faultmode

(a)蒸发器出口温度曲线(b)蒸发器出口湿度曲线(c)蒸发器出压力曲线(d)过热度曲线图4　故障模式下各输出比较Fig．4　Outputcomparisonwithfailuremode

5　结　论

针对电动汽车空调系统,建立了基于观测器的电动汽车空调系统，依据其执行器发生故障的模式,提出了汽车空调故障模型的H∞鲁棒控制器.充分考虑了执行器在系统运行过程中可能存在的失效、中断和偏移等问题,将故障模型化为系统的不确定性模型.通过采用线性矩阵不等式(LMI)工具设计对考虑执行器故障的H∞状态反馈鲁棒控制器进行设计,并且证明了闭环系统的稳定性.仿真结果表明:在有故障和无故障模式下的观测误差最大分别为0.1%和0.6%，满足系统的观测需求；与未考虑执行器故障的电动汽车空调H∞控制器相比，在10 Hz以下频段，考虑执行器故障的H∞控制方式可有效地抑制系统输入端所带来的干扰.

参考文献:

[1]JETTE I,ZAHEER-UDDIN M,FAZIO P.PI-control of dual duct systems:manual tuning and control loop interaction[J].Energy conversion and management,1998,39(14):1471-1482.

[2]QIAN W,PENG F Z,CHA H.Trans-z-source inverters[J].IEEE transactons on Power Electronics,2011,26(12):3453-3463.

[3]付龙海,李蒙.基于PID神经网络解耦控制的变风量空调系统[J].西南交通大学学报,2005,40(1):13-17.

FU Longhai,LI Meng.Variable-air-volume air-conditioning system based on PID-ANN decoupling control technology[J].Journal of Southwest Jiaotong University,2005,40(1):13-17.

[4]HOSOZ M,ERTUNC H M.Artificial neural network analysis of an automobile air conditioning system[J].Energy Conversion and Management,2006,47(11):1574-1587.

[5]ZHANG Q,CANOVA M.Modeling and output feedback control of automotive air conditioning system[J].International Journal of Refrigeration,2015,58:207-218.

[6]ZHANG Q,CANOVA M,RIZZONI G.Sliding mode control of an automotive air conditioning system[C]∥American Control Conference.[S.l.]:IEEE,2013:5748-5753.

[7]KEIR M C,ALLEYNE A G.Dynamic modeling,control,and fault detection in vapor compression systems[R].[S.l.]:University of Illinois at Urbana-Champaign,2006.

[8]任春晖.基于故障树分析的汽车空调系统故障诊断研究[J].中国农机化学报,2013,34(5):182-184.

REN Chunhui.Research of A/C Fault diagnosis based on failure tree analysis[J].Journal of Chinese Agricultural Mechanization,2013,34(5):182-184.

[9]ZHANG Q,CANOVA M.Fault detection and isolation of automotive air conditioning systems using first principle models[J].Control Engineering Practice,2015,43:49-58.

[10]刘占峰,宋力,赵丹平.汽车空调[M].北京:北京大学出版社,2011： 22-65.

[11]吴伟军,钟建法,彭仟能.并联涡旋式压缩机在空气源热泵机组中的应用分析[J].制冷与空调,2013(1):55-58.

WU Weijun,ZHONG Jianfa,PENG Qianneng.Application analysis of parallel scroll compressors for air-source heat pump chiller[J].Refrigeration and Air Conditioning,2013(1):55-58.

[12]MCKINLEY T L,ALLEYNEA G.An advanced nonlinear switched heat exchanger model for vapor compression cycles using the moving-boundary method[J].International Journal of Refrigeration,2008,31(7):1253-1264.

[13]FARZANEH Y,TOOTOONCHI A A.Intelligent control of thermal comfort in automobile[C]∥ 2008 IEEE Conference on Cybernetics and Intelligent Systems.[S.l.]:IEEE,2008:510-514.

[14]YANG Xiaozheng,YANG Guanghong.Robust adaptive fault-tolerant compensation control with actuator failures and bounded disturbances[J].Acta Automatica Sinica,2009,35(3):305-309.

[15]陈跃鹏,周祖德.广义系统的鲁棒控制与容错控制[M].北京:科学出版社,2010:41-46.

[16]金小峥,杨光红,常晓恒,等.容错控制系统鲁棒H∞和自适应补偿设计[J].自动化学报,2013,39(1):31-42.

Jin Xiaozheng,Yang Guanghong,Chang Xiaoheng,et al.Robust fault-tolerant control with adaptive compensation[J].Acta Automatica Sinica,2013,39(1):31-42.