基于SVM的流程图像角点分类

孙连山， 张沙沙， 侯　涛， 赵　晓

(陕西科技大学 电气与信息工程学院， 陕西 西安　710021)

0　引言

流程图代表着一个庞大的、有用的图像子集，可以直观地描述一个工作过程的具体步骤，具有重要的语义[1].流程图像中蕴含的丰富信息，对于检索和查新至关重要.基于图像匹配的检索技术已经得到了广泛关注[2,3].考虑到具有相同或相似语义的流程图布局多样，为了实现基于流程图像匹配的检索必须首先识别流程图像的语义，即将流程图像识别为描述流程图的文本信息.现有流程图像识别研究大体分为两类.一类是基于连通域的方法提取结构元素轮廓，然后通过轮廓拟合、BSM (Blurred Shape Model)、几何矩描述子等几何信息对结构元素逐一进行识别[3-5]；另一类采用矢量化方法提取结构中的边线和结构元素之间的结合点，基于直线段序列以及直线段与结合点之间的组合对流程图结构进行识别[6-8].这些方法虽然能较好地处理清晰的流程图像，但无法正确处理包含文图粘连和断边等情况的模糊流程图像.

角点是图像的重要局部特征，已被广泛应用于计算机视觉和图像处理的众多领域当中[9].流程图像中的角点是直线或曲线线条的交汇点.流程图的图元结构可表示为特定类型的角点组合，如矩形图元可表示为左上(┌)、右上(┐)、左下(└)、右下(┘)等四类角点的组合.流程图像的角点不受图文粘连和断边的影响，善加利用可以解决现有流程图像识别研究所面临的挑战.自动检测流程图像角点并正确地实现角点分类是充分利用角点特征识别和理解流程图像的基础.

现有角点检测算法只计算角点的位置，而未涉及角点分类.现有角点分类研究关注于一般图像的角点分类问题，所采用的分类方法也相对简单[10-13].如文献[10]根据角点邻域中不同等值线的梯度幅值将一般图像中的角点分为L、Y和X等类型；文献[11]根据角点的归一化各向异性方向导数将一般图像中的角点分为简单点，Y型角点和星形角点等；文献[12]根据角点两侧曲线段的曲率变化情况将角点分为6类，并基于有向面积对角点分类；文献[13]分析并定义了特定于视网膜血管图像的角点类型，包括终点、中间点、T型点、Y型点和交叉点，并采用矩形探测器识别血管分叉点和血管投影交叉点.现有角点分类研究所定义的角点类型不适用于流程图像理解，相应的角点分类方法也相对简单而不能对流程图像角点进行准确地分类.

本文结合流程图的结构特征，定义特定于流程图像的角点分类模型，然后采用经典角点检测算法得到候选角点，最后提取角点邻域的网格密度特征和外围特征，训练SVM分类器实现角点分类，为自动识别和理解流程图像奠定基础.

1　流程图角点类型分析

流程图包括两类典型结构元素，一类是具有规则几何形状的封闭图元，如矩形、菱形、平行四边形、椭圆、圆等；另一类是与图元相连的各类连接线，如直线、折线、箭头、扭线等.这些结构元素均由简单的直线或曲线构成，多条直线或曲线的交汇点就构成了流程图像的角点.如表1所示，在流程图像中的封闭图元、连接线、以及二者之间的连接处均可识别得到特定类型的角点.流程图像中的结构元素往往可抽象地表示为特定类型的角点组合.

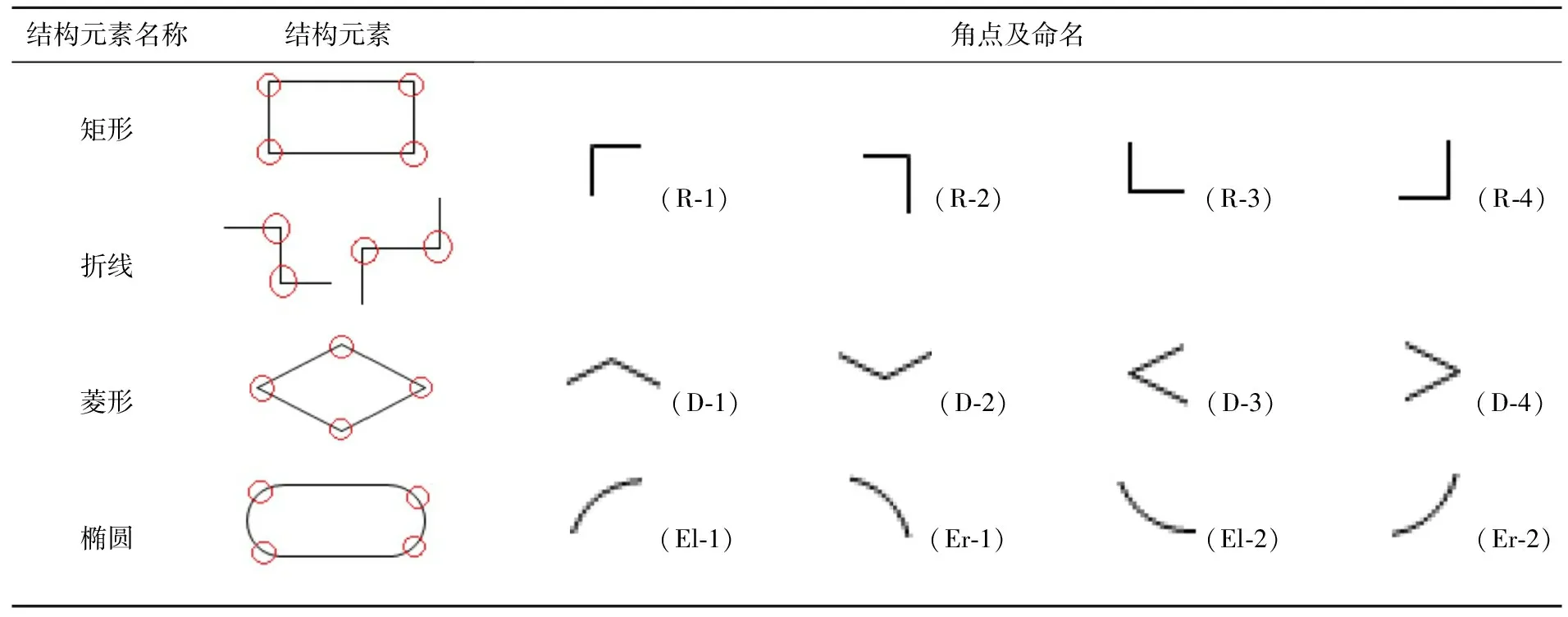
表1　流程图像角点分类

续表1

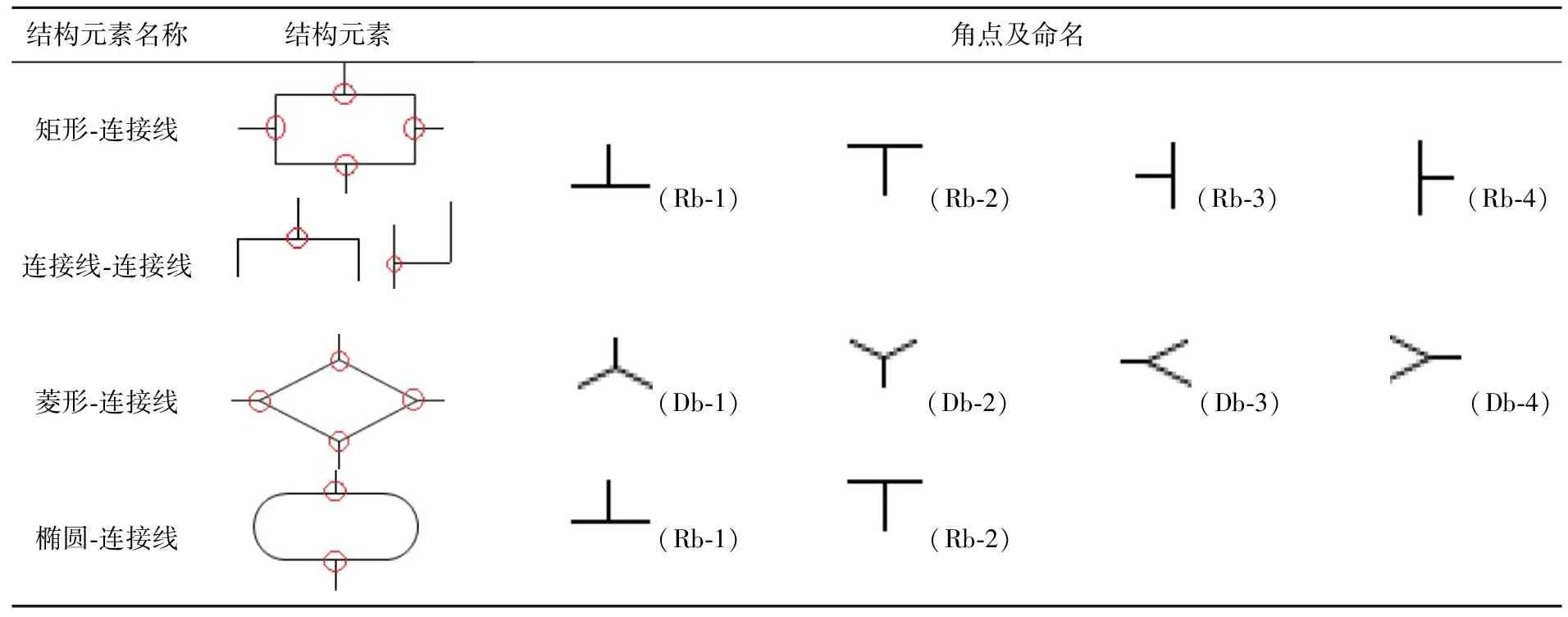
结构元素名称结构元素角点及命名矩形⁃连接线连接线⁃连接线(Rb⁃1)(Rb⁃2)(Rb⁃3)(Rb⁃4)菱形⁃连接线(Db⁃1)(Db⁃2)(Db⁃3)(Db⁃4)椭圆⁃连接线(Rb⁃1)(Rb⁃2)

表1分析并总结了可从八类典型的流程图结构元素组合模式中提取得到的角点以及这些角点的邻域图示.这些角点可分为两类，一类是仅属于单个图元或连接线的独立型角点，如表1中上半部分角点；另一类是位于图元和连接线连接处的连接型角点，如表1下半部分角点.根据角点邻域所蕴含的流程图像结构信息，可将角点进一步分类.如表1中与矩形相关的角点可分为四类，按照从上到下从左到右的顺序依次为┌(R-1)、┐(R-2)、└(R-3)、┘(R-4).折线上的部分角点与矩形独立型角点的邻域相同，将两种情况中的角点归为同一类.同样矩形-连接线与连接线-连接线模式中的角点也可以归为同一类.

2　角点检测

现有角点检测算法大致可以分为三类[9]：以Harris算法[14]为代表的基于灰度强度的方法，以曲率尺度空间(Curvature Scale Space，CSS)算法[15]为代表的基于边缘轮廓的方法，以及以SUSAN[16]算法为代表的基于模型的角点检测方法.这些方法各有优缺点，适用的对象也不同.

流程图结构元素可分为直线型元素和曲线型元素.直线型元素包括矩形、菱形和连接线等，其边缘轮廓局部曲率变化明显，实验表明采用基于边缘轮廓的方法(如CSS方法)即可以达到较理想的角点检测效果；曲线型元素多指圆或椭圆，其边缘轮廓局部曲率变化不明显，实验表明采用基于灰度强度的方法(如Harris方法)可避免真实角点漏检，再配合冗余角点筛除，即可达到较理想的角点检测效果.因此，本文采取CSS和Harris角点检测方法分别检测与直线型元素和曲线型元素相关的角点.未来应研究针对流程图的特定角点检测算法，进一步提高角点检测的全面性和准确性.

2.1　流程图结构提取

本文中提到的流程图像角点检测特指针对流程图结构图像的角点检测，识别这些角点对自动识别和理解流程图结构至关重要.因此，在获得原始流程图像之后，首先要进行图文分割，提取原始流程图像中的结构图层.

为了减少图像本身质量问题以及图像中文本对结构图像角点检测的影响，在开始检测角点之前，首先对流程图像进行二值化和降噪处理.其次，采用连通域标记算法[17]，计算并删除面积小于指定阈值的连通域以去掉文字，实现图文分割，得到流程图结构图像；最后，为减少边线粗细对角点检测的影响，对提取的流程图结构图像进行单像素化[18].图1展示了在真实流程图中注入文图粘连以及断边情况后的流程图结构提取效果.显然，文图粘连影响结构元素的整体轮廓，无法基于轮廓正确识别结构元素形状.但如图中圆圈标记部分所示，能够组成菱形和矩形的角点位置和类型则未受影响，结构元素的角点组合基本完整保留下来，达到了结构提取的目的.

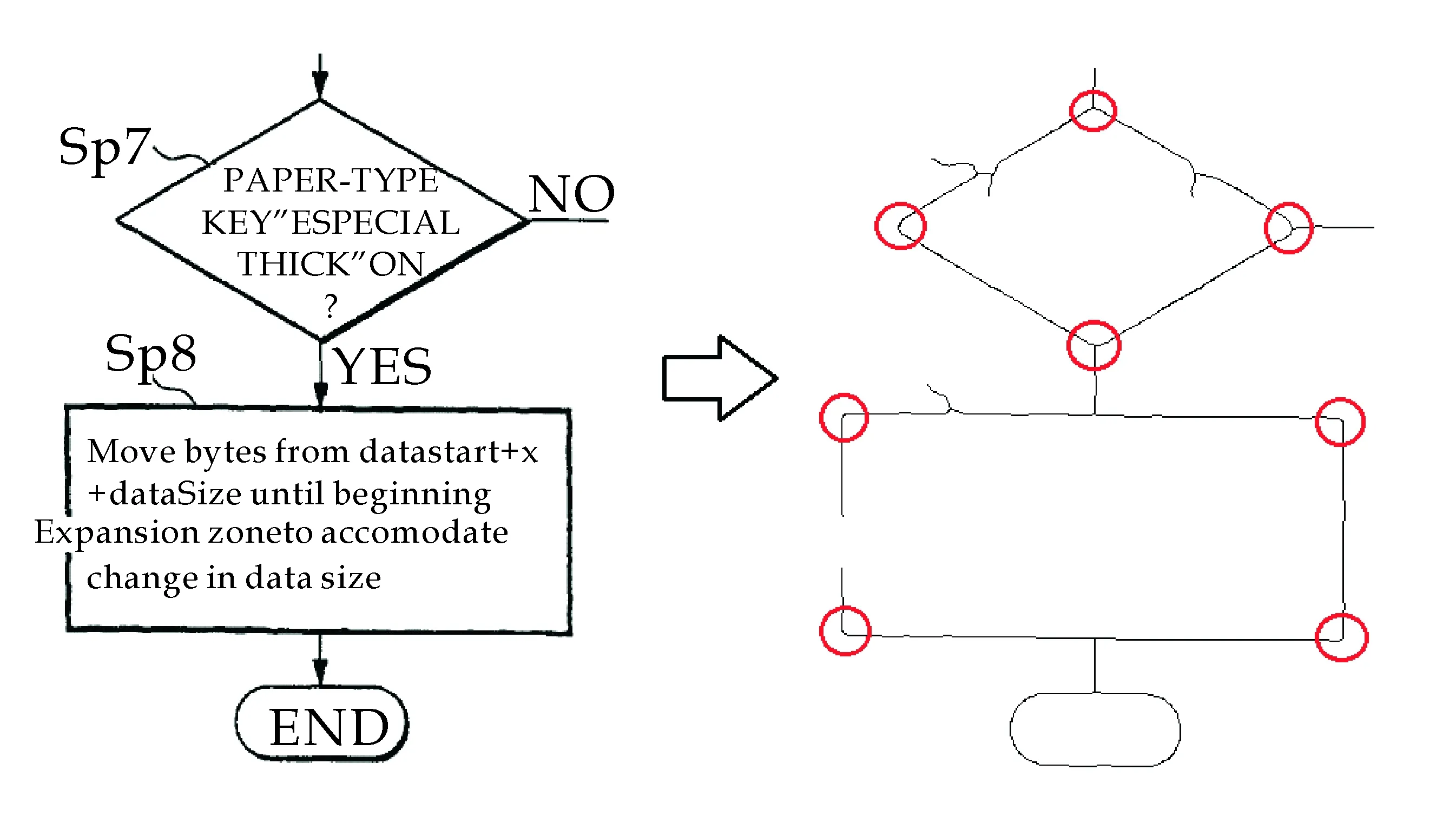
图1　流程图结构提取

2.2　基于CSS的直线型结构元素角点检测

CSS 算法将不同尺度下图像边缘轮廓曲线的局部曲率极大值点作为候选角点，然后在多个尺度下跟踪定位角点.对于一条平面曲线l，不同尺度σ下的曲率.

(1)

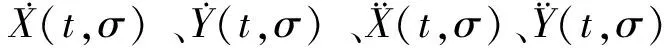
采用CSS算法在同一尺度不同曲率下对流程图像结构元素进行角点检测的效果显示，直线型结构元素上的角点检测全面准确，而曲线型结构元素上的角点随曲率变化出现定位不准及漏检情况.为了采用CSS算法获得直线型结构元素上的准确角点，本文将曲线型结构元素上的角点视为圆角点并同虚假角点一起过滤掉.下面分别介绍圆角点及虚假角点的判定方法.

(2)

式(2)中：u为候选角点的位置参数，K(u)是候选角点的曲率，T(u)为与角点支持域自适应的动态局部阈值，与候选角点u处的局部平均曲率成正比.当Rc=1时表示角点为圆角点，给予滤除.

(3)

式(3)中：Cc为需要判定的候选角点，∠Cc为角点Cc的角，θobtuse为真正角点的最大钝角值，实验中设θobtuse=162°，当Cc>θobtuse时，Cc为虚假角点.

2.3　基于Harris的曲线型结构元素角点检测

Harris算法通过判断角点的响应函数值来确定角点存在与否，对于纹理丰富的曲线边缘可以提取出大量有用的角点.本文采用Harris算法针对曲线型结构元素进行角点检测.

流程图中曲线型结构元素基本位于整体结构中周边位置，对已经识别的角点进行边界搜索并覆盖掉边界包围的区域得到流程图中未识别的结构元素，然后采用Harris角点检测算法对CSS角点检测方法未识别的曲线型结构元素再进行检测.

在检测过程中，曲线上容易产生角点聚簇现象.针对此问题，本文采用距离筛选方法，计算所有点之间的欧式距离.当两个候选角点间的距离小于指定阈值时，可删掉其中之一以减少冗余.

3　角点分类

3.1　角点特征提取

角点邻域蕴含丰富的结构信息，是对角点进行分类的依据.首先，以检测到的每个角点为中心截取一定大小像素的角点邻域图像；其中经过实验验证，当以角点为中心点向四边扩展20像素得到41×41像素的角点领域图像能更好的体现出角点的特征区别；其次，参照汉字识别中的特征提取方法，提取角点邻域图像的网格特征和外围特征[20].

网格特征是指将二值化后的图像等分为n×n个网格后，每个网格内目标像素所占比例.虽然网格特征能较好地反映图像内部区域特征信息，但仍存在网格特征相似但不同类型的角点.即采用单一网格特征不能充分体现角点间的差异.

外围特征是指将图像从四边分别向对边进行扫描，每一边分为m个区域，计算每个区域碰到指定目标的面积占整个面积的比值.外围特征主要反应了角点的轮廓特征，为了加强角点细节特征的描述，分别计算一次外围特征与二次外围特征.一次外围特征是计算从开始扫描到第一次碰到目标的面积占整个面积的比值；二次外围特征是计算第一次穿过目标边与第二次再次碰到目标边之间的面积占整个面积的比值.

网格与外围特征结合可以较好地描述角点邻域所蕴含的结构信息.具体来讲，将角点n×n等分，计算n2维网格特征，然后再从4个方向计算每个m区域的一次和二次外围特征，构成2×4×m维特向量，最终从角点邻域提取得到一个n2+8×m维的特征向量.本文根据实验效果决定n和m的实际取值.

3.2　基于角点的SVM分类

流程图像角点分类属于多类分类问题，可采用支持向量机(Support Vector Machine,SVM)予以实现.SVM本身是一个二值分类器，可以通过组合多个二分类器来实现多分类器的构造，主要方法有one-against-one(1-a-1)，one-against-rest ( 1-a-r)，决策树SVM( DTSVM)等方法[21],本文采用1-a-1方法构建多类分类器.SVM的基本思想是通过核函数将低维不可分数据映射到高维特征空间来解决非线性可分问题.其本质是求解核函数和二次规划问题.

SVM是一种监督学习方法，在提取角点样本特征后，应将角点样本分类标注，作为SVM分类器的训练样本集.本文采用径向基核函数(Radial Basis Function,RBF)作为SVM分类的核函数.RBF核函数具有较宽的收敛范围，是较理想的分类依据函数，可以将一个样本映射到一个更高维的空间.利用MATLAB中的LIBSVM工具箱来实现SVM多分类，其中在目标函数里引入惩罚因子c对其进行惩罚，体现重视离群点带来损失的程度.通过参数调优设置惩罚因子c，使得数据在高维特征空间中的线性可分度最大.

3.3　交叉验证

使用RBF核时需要两个参数：(c,g)，惩罚系数c是对误差的宽容度，值越高，说明误差越小；g是选择径向基函数作为核函数后该函数自带的一个参数，决定了数据映射到新的特征空间后的分布.由于预先并不知道哪一对和是最佳的，因此必须要进行参数搜索,目标是确定一对好的(c,g) ,使分类器能够正确地预测未知数据.因此,常见的方法是把训练数据分成两部分,一部分作为未知数据，在这批数据上的预测精度很大程度上反映了对未知数据的分类性能.对这一过程的改进,即交叉验证.本文用的是K-折交叉验证(K-fold CrossValidation，K-CV).将原始数据均分成K组，将每个子集数据分别做一次验证集，其余的K-1组子集数据作为训练集，这样会得到K个模型，用这K个模型最终验证集的分类准确率的平均数作为此K-CV下分类器的性能指标.

4　结果与分析

本文关注流程图像的角点检测和分类，与针对一般图像[10-12]、血管图像[13]的角点检测方法在角点模型、检测方法上存在较大差异，无法直接对比.因此，本节仅介绍针对本文方法的实验验证与总结分析，包括实验数据、实验方式、实验环境以及实验结果分析等.

实验数据来源于CLEP-IP 2012[22]，其公开的数据集包括从真正的文献中获取的150张流程图，所有图像都是二值形式并且仅包含单一的流程图.实验中选取其中50张流程图，结合从网络上爬取的50张流程图共100张作为实验对象.实验平台为MATLAB R2014a，Intel(R) Core(TM) i3处理器，4 GB内存，Windows 7操作系统.

4.1　角点检测实验分析

将流程图预处理后根据连通域面积实现文图分割提取流程结构图像，针对其中直线型和曲线型结构元素采用CSS和Harris结合的角点检测方法，实验效果如图2所示.

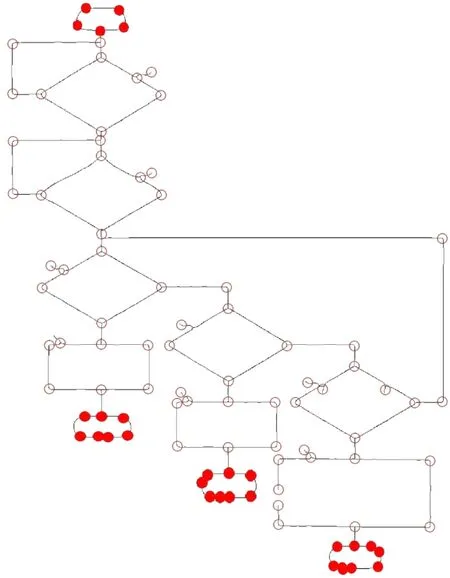
图2　角点检测实验结果

CSS角点检测方法对流程图中直线型元素可以达到理想的角点检测效果(空心角点)，Harris角点检测方法针对曲线型结构元素检测时出现冗余，经过筛选可减少冗余角点并保留E图元的绝大部分角点结构信息(实心角点).

得到候选角点后获取角点邻域图像，然后对其进行分类标注.在实际检测到的流程图像角点中，除表1中总结的构成结构元素的重要角点以外，还有来自预处理后保留的箭头上的角点、直线上噪点产生的角点、斜线上误检的角点以及曲线上冗余的角点.如图3所示，前三行为实验中出现的表1中总结的角点，后两行为实验中出现的其他类型角点.按照角点类型命名中第一个参数分为A、D、Db、Eb、E(包括El与Er)、L、R、Rb 8类.

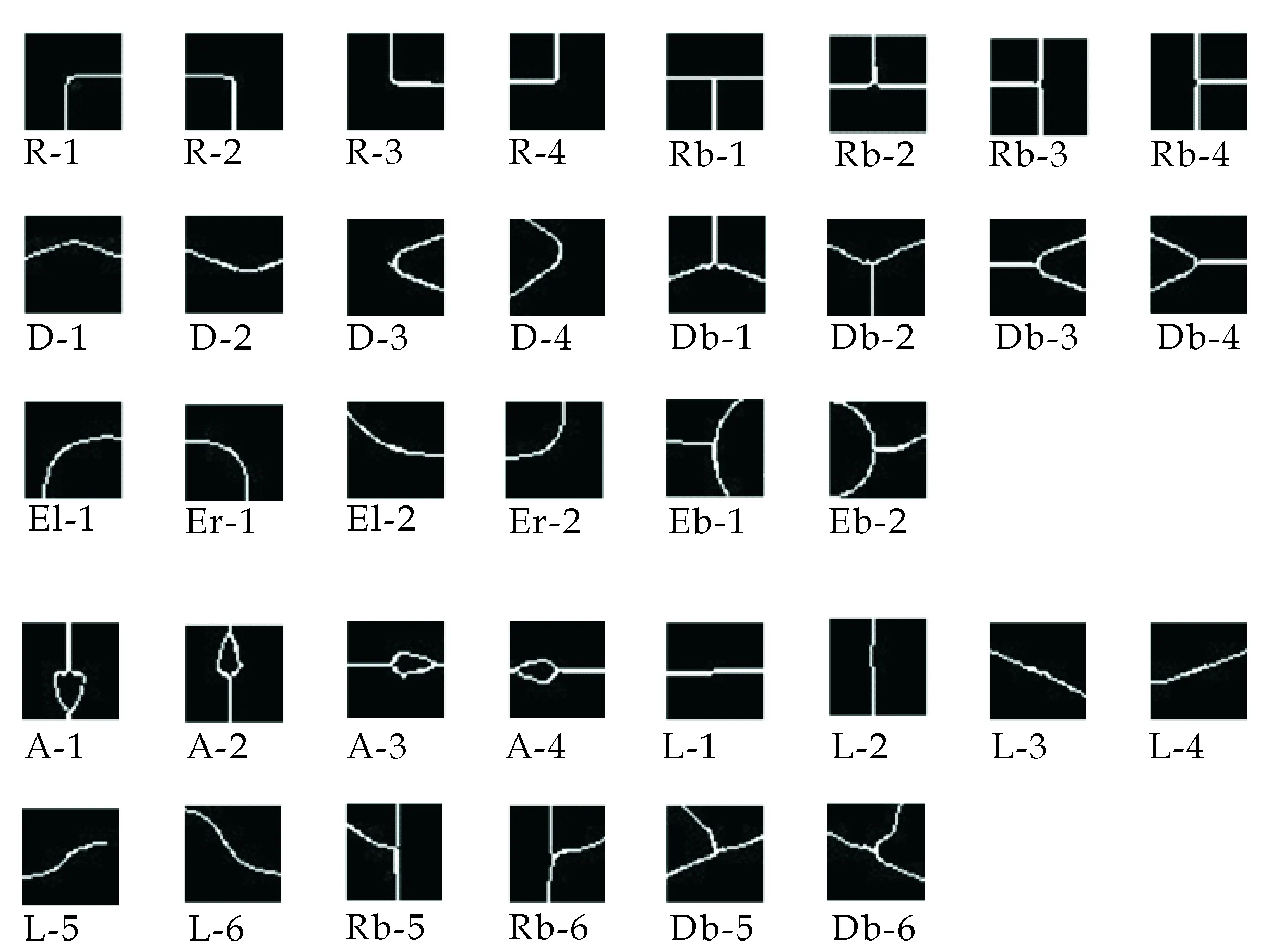
图3　实验中出现的流程图像角点

4.2　角点分类实验分析

对角点进行特征提取，实验中采用不同维数特征进行结果对比.由表2所示，m为计算外围特征时每边划分的区域数，n为角点等分网格化参数，特征向量维数为n2+8×m.实验中截取的2 000张角点图像作为训练集TrainData，650做测试集为TestData.提取不同维数的特征采用LIBSVM进行角点的多分类并统计实验结果如表2所示.实验表明，随着特征维数提高，训练集的角点识别率不断提高，而过拟合使得测试集角点识别率下降.因此，实验采用m和n取8时角点分类结果.首先将角点图像8×8等分，计算网格特征构成64维特征值，再将图像4×4等分，分别从4个方向扫描得到外围特征构成64维特征值，最后每一个角点可以用128维特征值表示.

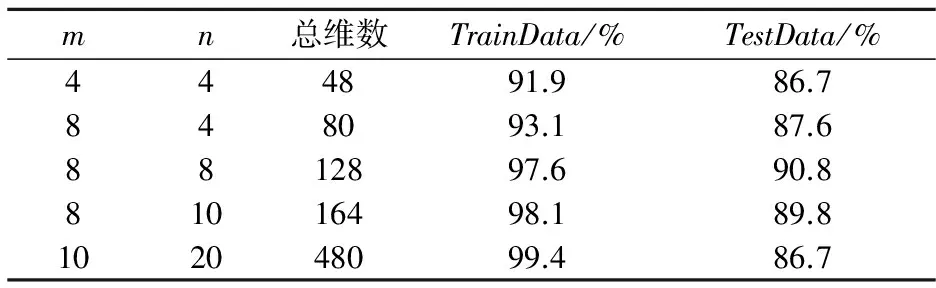
表2　不同特征维数的角点识别率

对于SVM参数的优化，本实验选择网络搜索优化方式，利用LIBSVM中grid.py参数工具，可以自动进行参数寻优，最终得到最佳参数

c=3.031 25，g=9.007 812 5.

利用参数工具得到的c，g值在SVM中建模，对角点类型进行预测.将实验数据集均分为5组，每组角点520张.在分类过程中，根据角点本身类型(真/假)以及检测结果(真/假)，可能出现以下几种情况：本身是真，检测结果也为真(TP)；本身是真，检测结果为假(FN)；本身是假，检测结果为真(FP).计算角点检测查准率(P)和查全率(R)来分析检测结果：

查准率(P)：检测到的真角点数占实际真角点数的百分比，即

(4)

式(4)中：TP是检测结果为真且本身为真的角点个数；FP为检测结果为真但本身为假的(被误检)的角点数.

查全率(R)：检测到的真角点数占应该被检测到角点数的百分比，即

(5)

式(5)中：FN为本身为真而检测结果为假的角点数.

实验对5组角点数据集采用交叉验证方式，角点检测结果如表3所示.根据每一组训练集来进行测试集角点类型的检测，并计算查全率和查准率以及每一角点类型的平均值.从实验结果总结分析，对测试集角点分类结果较理想，对5组中8类角点的实验结果求均值得到查准率为89.1%，查全率为91.6%.其中曲线型结构元素角点(E，Eb)相对于直线型结构元素角点的识别率低，直线型结构元素中Rb以及角点特征相对复杂的A角点查准率也相对较低.查全率和查准率低的原因有三个：一是曲线形结构元素的角点检测受限于目前角点检测技术，角点检测定位不精确并出现冗余问题；二是E图元本身尺度问题使得曲线局部角点特征有曲度差异，例如经过预处理后得到的曲率较大的El-1角点与R-1角点会容易误检测；三是在实际流程图中存在角度不同以及形式多样问题，细分种类较多，样本差距越大SVM对数据拟合程度不够，分类性能也就变差.

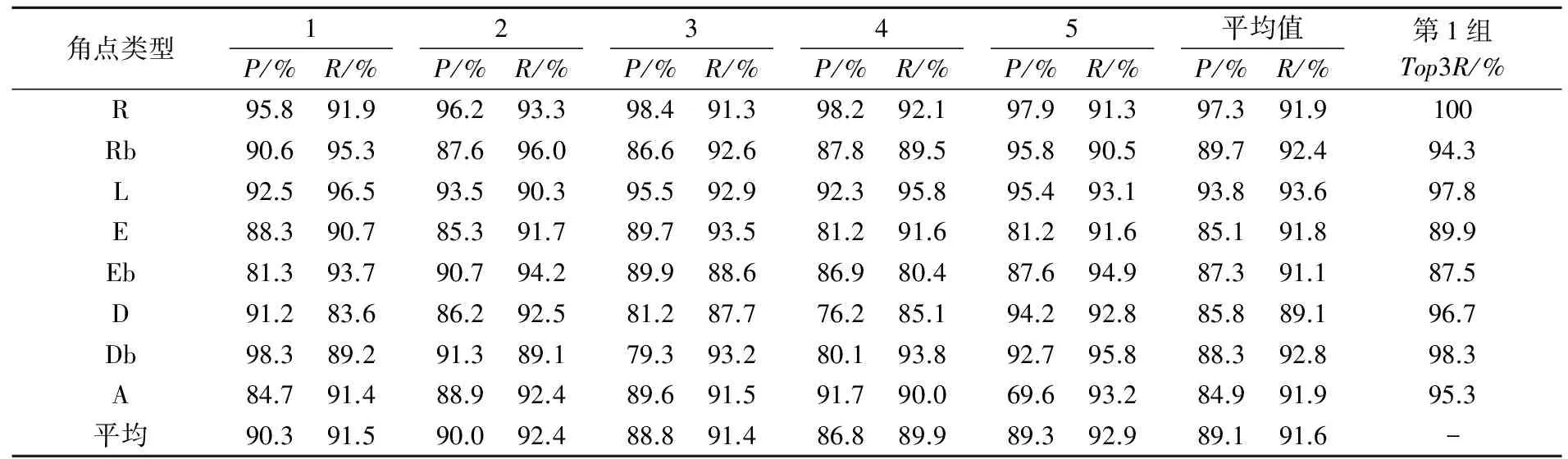
表3　各组角点分类结果

为了降低角点误分类对后续流程图结构识别和理解的影响，对LIBSVM中预估函数返回的每个角点不同类型的分类概率做统计，将较高分值的前几位所对应的类型依次作为预测值的候选类型，

以此提高角点类型预测准确率.表3中统计第一组角点数据集的前三位候选类型(Top3R)查全率.结果表明，三候选角点类型中对各类角点类型预测准确率有明显提高.

5　结论

提出了一种针对流程图像的角点检测与分类方法，从角点特征分析流程图像并定义流程图像角点分类模型，采用角点邻域的网格特征和外为特征训练SVM分类器实现角点分类.针对公开数据集图像的实验表明采用CSS与Harris结合的方法可以全面准确地检测流程图角点，并达到较好的角点分类结果.本文的研究成果为进一步开展基于角点的流程图识别研究工作奠定基础.

[1] Bhatti N,Hanbury A.Image search in patents:A review[J].International Journal on Document Analysis and Recognition (IJDAR),2013,16(4):309-329.

[3] Adams S.Electronic non-text material in patent applications-some questions for patent offices,applicants and searchers[J].World Patent Information,2005,27(2):99-103.

[5] Thean A,Deltorn J M,Lopez P,et al.Textual summarisation of flowcharts in patent drawings for CLEF-IP 2012[J].Aorn Journal,2012,32(2):1-21.

[6] Escalera S,Forn,Alicia S,et al.Blurred shape model for binary and grey-level symbol recognition[J].Pattern Recognition Letters,2009,30(15):1 424-1 433.

[7] Roland M,René S,Andrs H,et al.Visual structure analysis of flow charts in patent images[C]// CLEF2012 Evaluation Labs and Workshop.Roma,Italy:Online Working Notes,2012:115-133.

[8] Sas J,Markowska Kaczmar U.Logical structure recognition of diagram images[C]//2015 Federated Conference on Computer Science and Information Systems.Lódz,Poland:FedCSIS,2015:215-224.

[9] 章为川,孔祥楠,宋文.图像的角点检测研究综述[J].电子学报,2015,43(11):2 315-2 321.

[10] Ryu J B,Park H H,Park J.Corner classification using harris algorithm[J].Electronic Letter,2011,47(9):536-538.

[11] Shui L,Zhang W C.Corner detection and classification using anisotropic directional derivative representations[J].IEEE Transaction on Image Processing,2013,22(8):3 204-3 218.

[12] 曾接贤,黄华川,张桂梅.基于有向面积的角点分类算法[J].中国图象图形学报,2008,13(6):1 159-1 165.

[13] 赵晓芳,林土胜.视网膜血管图像特征点自动提取和分类[J].计算机工程与应用,2011,47(8):14-17.

[14] Zhang C P,Wei X G.Rectangle detection based on Harris corner[J].Optics & Precision Engineering,2014,152(3):3 479-3 491.

[15] Zhang X,Lei M,Yang D,et al.Multi-scale curvature product for robust image corner detection in curvature scale space[J].Pattern Recognition Letters,2007,28(5):545-554.

[16] 韩建峰,宋丽丽.改进的字符图像细化算法[J].计算机辅助设计与图形学学报,2013,25(1):62-66.

[17] He L,Ren X,Gao Q,et al.The connected-component labeling problem:A review of state-of-the-art algorithms[J].Pattern Recognition,2017,70:25-43.

[18] 王家隆,郭成安.一种改进的图像模板细化算法[J].中国图象图形学报,2004,9(3):297-301.

[19] Awrangjeb M,Lu G.An improved curvature scale-space corner detector and a robust corner matching approach for transformed image identification[J].IEEE Transactions on Image Processing,2008,17(12):2 425-2 441.

[20] 刚亚州,黄元元,戴群.一种快速名片字符识别算法[J].计算机应用研究,2014,31(9):2 859-2 863.

[21] 王道明,鲁昌华,蒋薇薇,等.基于粒子群算法的决策树SVM多分类方法研究[J].电子测量与仪器学报,2015,29(4):611-615.

[22] Piroi F,Lupu M,Hanbury A,et al.CLEF-IP 2011:Retrieval in the intellectual property domain,September 2011[DB/OL].http://www.ifs.tuwien.ac.at/ ～clef-ip/download/2012/ index.shtml,2012-09-04.