基于拓扑优化的FSAE赛车车架结构设计

吴佳秜，张诗博*，解紫婷，陈浩杰

（1.成都农业科技职业学院机电技术分院，四川 成都 611130；2.南昌大学，江西 南昌 330031）

引言

近年来，中国对汽车工业发展愈加重视，电动方程式赛车车队的要求便不仅仅局限于造出一辆的车，而着眼于打造一辆性能优异的赛车。车架作为一辆车受力、传导力的重要结构部件，便对其有了更高的性能要求。本文主要着重于车架的设计与拓扑优化，把如何设计一个兼顾轻量化与安全性的车架作为本文研究的目标。

拓扑优化中的连续体拓扑优化对于桁架结构比较适用。连续体拓扑优化把定义空间分割成有限个单元进行设计，WEI K L[1]利用连续体拓扑优化中的变密度法对半挂车车架进行优化设计对变密度法进行了详细讨论，并给出了优化结果。CHEN C F[2]等对抑制棋盘格现象而引入的惩罚因子ρ作了描述，对结果进行的验证也证明了其可靠性。

本文对FSAE赛车桁架式车架采用连续体拓扑优化的方法，建立有限个PSHELL单元和PBEAM单元的拓扑优化模型，借鉴与优化结果设计出兼顾轻量化与安全性的新车架，再对新车架进行力学及模态分析，保证车架结构满足设计要求，可以安全参赛。

1　车架初步设计与建立有限元模型

1.1　车架初步设计

在CATIA软件中建立了车架的最初模型。由于本车架采用钢管桁架结构，故车架的设计从钢管型号选择，桁架空间结构设计，人机工程等方面考虑。本文初步设计的车架依据规则要求以及理论分析使用三种不同尺寸的 4130Cr钢（弹性模量 E = 2.11×105MPa，泊松比μ=0.279，密度ρ=7850kg/m3，屈服强度σs(MPa)=785，初步车架的总质量约为40Kg），人机工程则根据CATIA人机工程学模块与1: 1PVC管模型进行设计。

1.2　有限元模型的建立

有限单元法（FEM）是一种可以精确预测复杂结构在外界载荷作用下响应的方法，分析步骤分为：前处理、求解、后处理。本文将使用有限元分析的方法进行车架结构的设计。将CATIA模型导入至有限元分析软件HyperWorks中，利用Hypermesh对其进行前处理。由于车架属于桁架结构，故使用1D梁单元进行网格的划分[3-4]。为减少计算量，在车架重要结构上，使用尺寸较小的单元进行划分，尺寸为5mm，对于受力较小的部分使用尺寸较大的单元划分，尺寸为10mm，网格的好坏直接决定结果的精确性，故在划分完成后需仔细检查网格质量。在划分网格时，经常会由于网格不连续带来的求解失败或者结果很差，所以本文使用CATIA软件中的创成式曲面设计模块把所有桁架结构所有交点进行打断，然后在 Hypermesh中的 Edges面板点击 preview equiv再点击equivalence，可以查找并闭合所有大节点，得到较优的梁单元网格。在网格划分时注意梁单元的方向性，有利于求解出正确的结果。

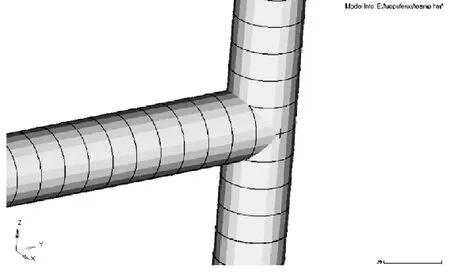
图2　连续的梁单元网格Fig.2 Continuous tube element mesh

2　初步车架刚度与自由模态分析

2.1　刚度分析

衡量车架力学性能指标的两个重要因素为弯曲刚度与扭转刚度[5]，刚度过低则容易造成车架在行驶过程中有较大的变形，不利于赛车的操控性，而且形变过大容易造成金属疲劳，安全性能下降。刚度过高则不利于整车轻量化。参照国内外高水平车辆，一般来说，扭转刚度在1000～5000 N·m/(º)左右，弯曲刚度在50000～150000 N·m/(º)左右为较优性能。本文加载的边界条件为：固定后悬架硬点全部六个自由度，对前悬左右硬点分别施加5000N的方向相反的力以及5000N方向相同的力[6]。

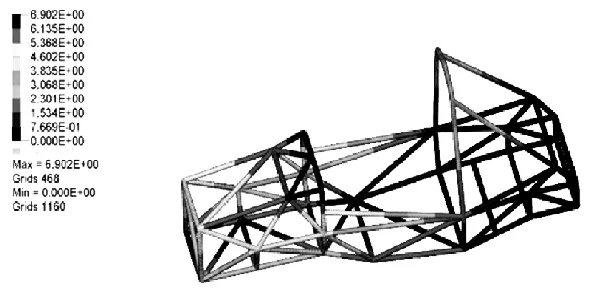
图3　初步车架的扭转云图Fig.3 The preliminary frame of the reverse figure

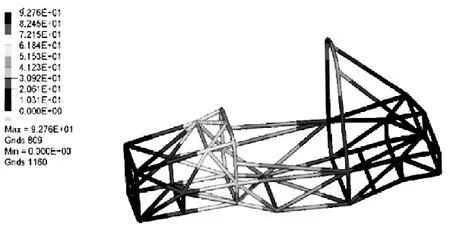
图4　初步车架的弯曲云图Fig.4 The frame curve displacement diagram

图为初步车架扭转位移图与弯曲位移图，可得到扭转刚度为：4870 N·m/(º)弯曲刚度为：98580 N·m/(º)[7]，发现扭转刚度过高。

2.2　自由模态分析

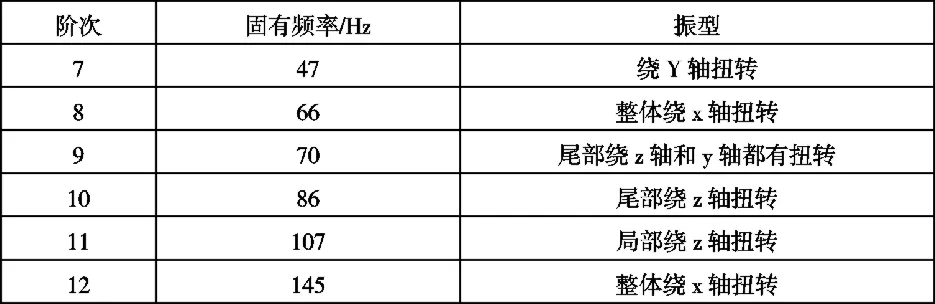
表1　初步车架固有频率表Tab.3 Natural frequency of the frist frame table

通过Hyperworks软件对初步车架进行自由模态分析，求解出初步车架前12阶模态频率，观察结果发现前六阶频率数量级非常小，可近似看为刚体振型[8]，后六阶频率与振型如表所示。得到的扭转刚度、弯曲刚度、固有频率作为参照组与拓扑优化后的车架参数进行对比。

3　拓扑优化分析

3.1　拓扑模型的建立

依据对初步车架的有限元分析结果的研究，为了简化拓扑分析的模型，在 CATIA软件中对受力较差的结构进行删除，保留基本结构以及受力较为优良的管件，再依据这些管件生成一个类似于单体壳的一个由面包络的车架，仅保留主环前环等规则限定结构。导入至Hyperworks软件中，选择求解器时我们选择 OptiStruct求解器，因为在处理多工况下的拓扑优化时，此求解器采用的为加权线性法[9]，在求解结果文件中我们可以看到不同的工况所占权重，对此进行调整，循环进行求解。在此求解器中定义包络的面为拓扑设计空间，其余为非设计空间。使用2D PSHELL单元对设计空间进行网格划分[1]，定义网格为矩形，由于为需优化结构，单元尺寸可适当缩小为10mm，厚度为8mm，再使用1D 梁单元对非设计空间进行网格划分，由于为非优化结构，单元尺寸可适当放大为 15mm。建立车架的拓扑优化模型。该模型包含36457节点，36105个单元。

3.2　设计变量的创建

由于车架的扭转刚度往往是考量车架性能的重要指标，故在施加载荷与约束时，我们先施加多种常见的的扭转方式去求解初步分析结果。再对结果进行考量，观察结构是否合理等，再添加其他的约束条件，如此不停反复修改，最终达到一种合理的结构，如图5所示。

在创建完边界条件之后，需要定义一个设计变量，包括最大化刚度以及最小化质量。在 OptiStruct中最大化刚度是以最小化柔度来体现的[9]。柔度C可以以以下关系式得到：

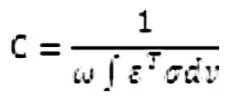
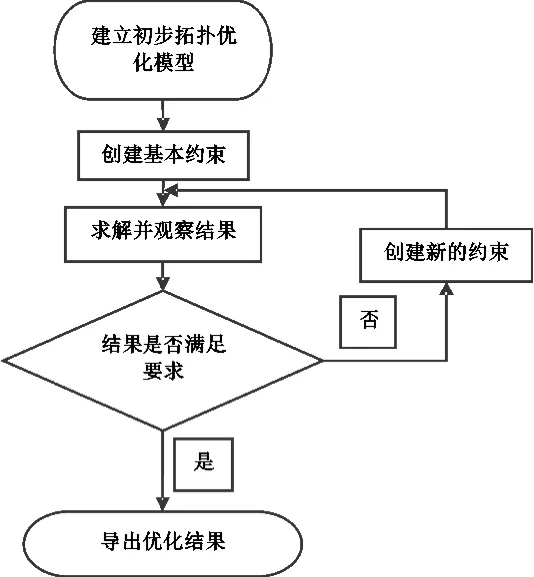
图6　拓扑优化流程Fig.6 Topology optimization process

其中，柔度C是结构的应变能，可以认为柔度是刚度的倒数。在本文中，柔度指定为与全部工况相关，来求解最大化刚度，因为最大化刚度不能以一个数值体现[9]，求解结果是发散的，所以巧妙地使用刚度的对立面柔度来体现。在创建最大化刚度这一个响应中，针对不同的工况可以使用Weighted comp面板依据经验对多个工况加权处理，在创建最小化质量这一个响应中，分析后发现取质量分数为0.21使可以得到更好结果。在设置成员尺寸时，经过不断地尝试，发现最小成员尺寸设置为 50mm，最大成员尺寸为最小成员尺寸为最小成员尺寸的两倍即100mm时可以得到更好结果。

3.3　拓扑优化结果与分析

分析中我们创建了纯扭转工况、弯曲与扭转复合工况、转弯与弯曲复合工况。

图7　纯弯曲拓扑优化结果Fig.7 Topology optimization results of Torsion

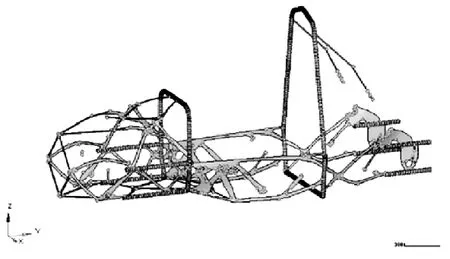
图8　扭转与弯曲拓扑优化结果Fig.8 Topology optimization results of torsion and bending

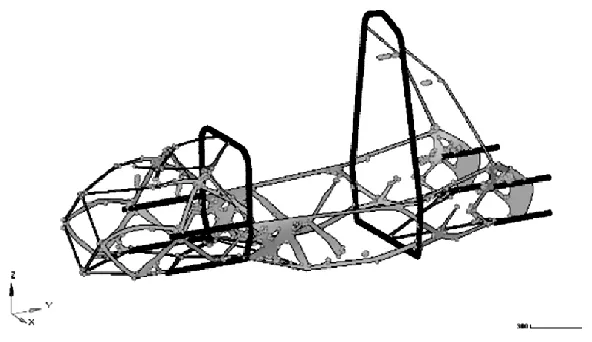
图9　扭转与转弯拓扑优化结果Fig.9 Topology optimization results of torsion and turn

图6是在纯扭转工况下经过42次迭代求解的结果，分析发现，此工况下除后舱外形成了较为明显的材料分布，前舱和座舱轮廓清晰。图7是扭转与弯曲的复合工况经过30次迭代求解的结果，对比图 6，出现了较为明显的后舱结构，主环斜撑支撑也出现了，这与初步车架弯曲刚度的有限元分析显示的应力在此处较大的结果一致，表明此拓扑优化模型有很大的可信度。图8是转弯与扭转的复合工况经过32次迭代求解的结果，分析发现，在后舱出现了明显的底板结构，在后悬安装点上材料分布比较密集，故设计时可以使用更高规格的钢管。

3.4　车架结构的重新设计

分析以上三种结果可知，由于求解为最大刚度，故很多地方出现了交叉结构，虽然这有利于大大提升车架刚度，但非常不利于车架轻量化，故重新设计时我们简化为单根支撑杆件。对于材料分布较少的地方我们使用低规格的钢管，对于材料分布密集的地方我们使用高规格的钢管，则新车架的钢管类型改进到了7种规格。改进后的车架结构如图9所示。

优化后车架的质量降低为30Kg，对于车架的轻量化起到非常有利的作用。

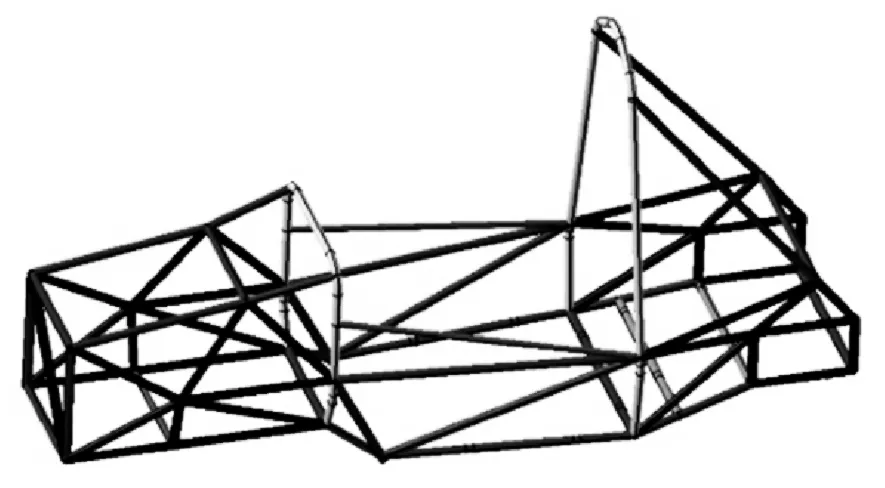
图10　新车架三维模型Fig.10 The new frame 3D model

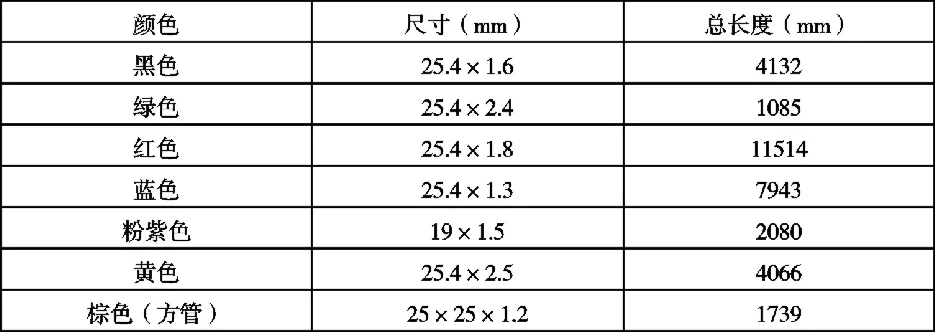
表2　新车架钢管规格表Tab.1 The new frame steel pipe specification table

4　优化后的车架分析

4.1　刚度分析

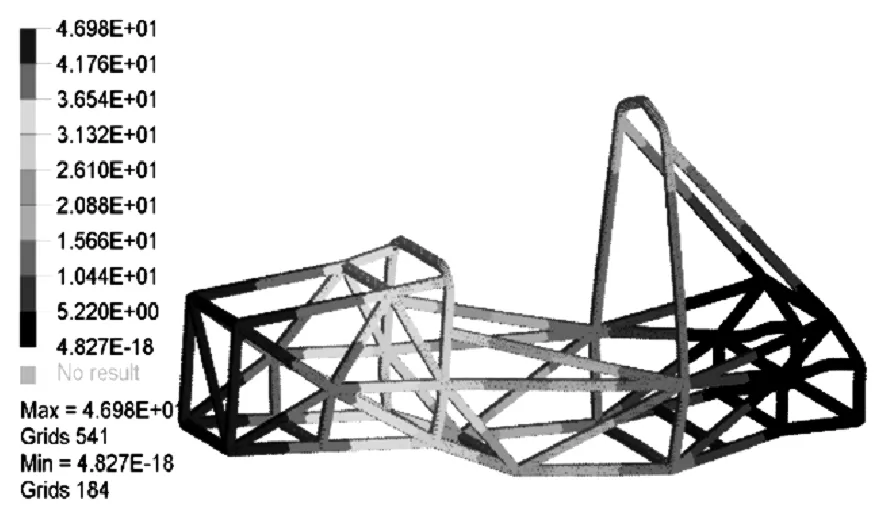
图11　新车架弯曲位移云图Fig.11 The new frame curve displacement diagram

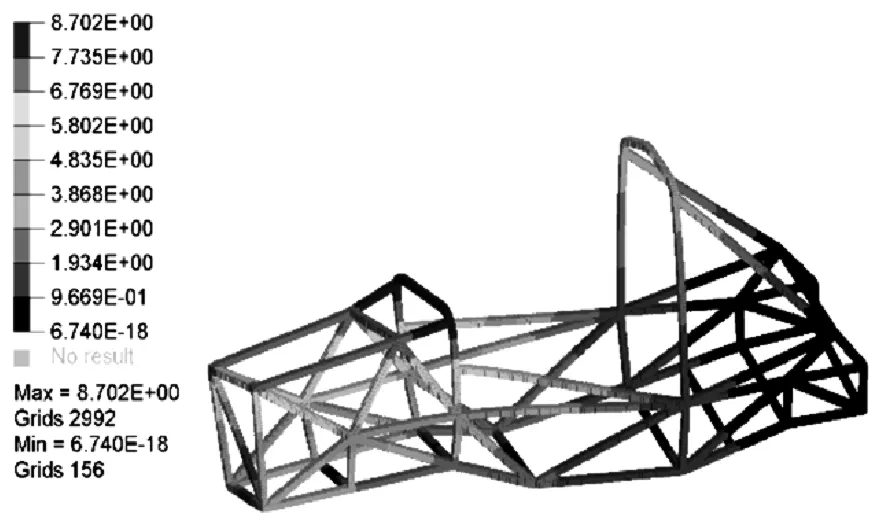
图12　新车架扭转位移云图Fig.12 The new frame torsional displacement diagram

图11与图12为新车架扭转与弯曲位移图，可得到扭转刚度为：3520N·m/(º)弯曲刚度为：86438 N·m/(º)[10]，由此可见，新车架刚度在允许范围内略有下降。

4.2　自由模态分析

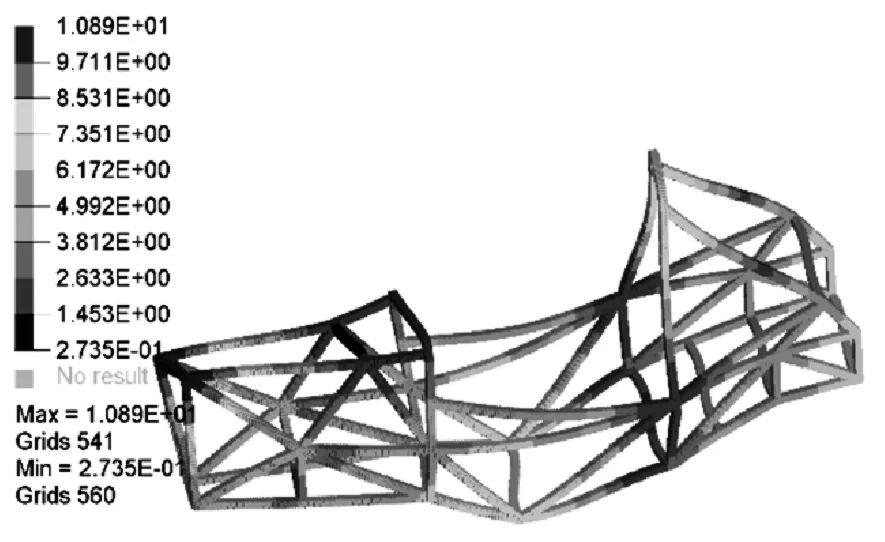
图13　新车架第7阶振型Fig.13 The new frame 7 order vibration mode

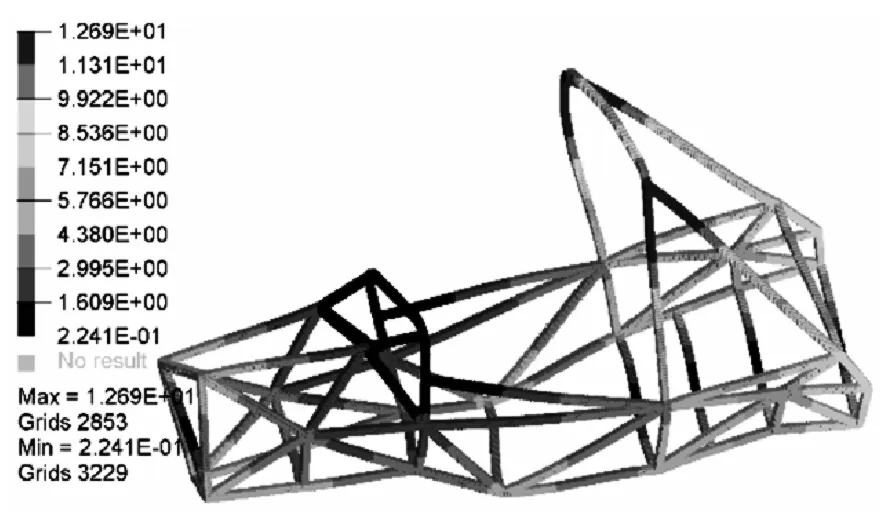
图14　新车架第8阶振型Fig.14 The new frame 8 order vibration mode

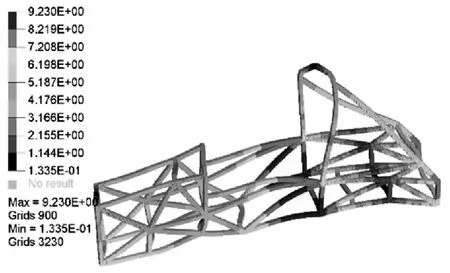
图15　新车架第9阶振型Fig.15 The new frame 9 order vibration mode

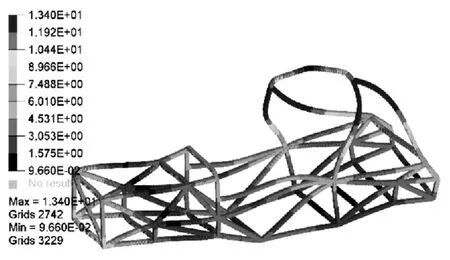
图16　新车架第10阶振型Fig.16 The new frame 10 order vibration mode

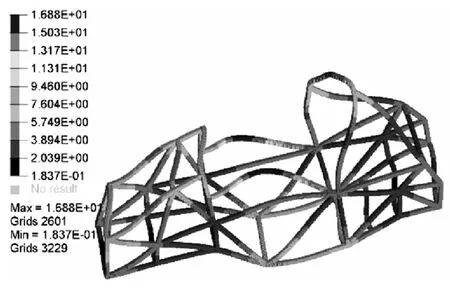
图17　新车架第11阶振型Fig.17 The new frame 11 order vibration mode

图18　新车架第12阶振型Fig.18 The new frame 12 order vibration mode

将新车架在Hyperworks软件中进行自由模态的分析，求解出车架前12阶模态频率，观察结果发现前六阶频率数量级非常小，可近似看为刚体振型[11]，后六阶频率与振型如下表所示。

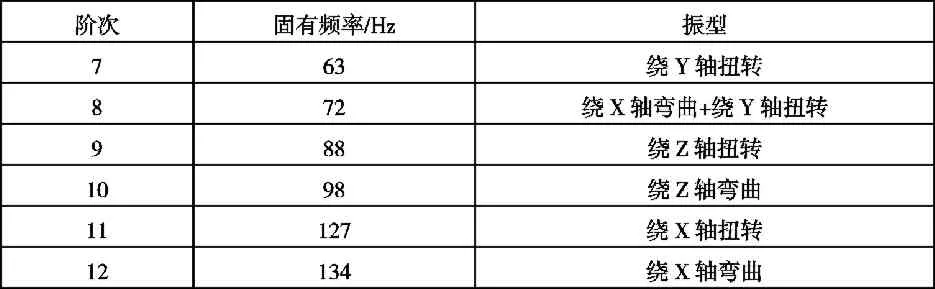
表3　新车架固有频率表Tab.3 Natural frequency of the new frame table

4.3　与优化前车架对比

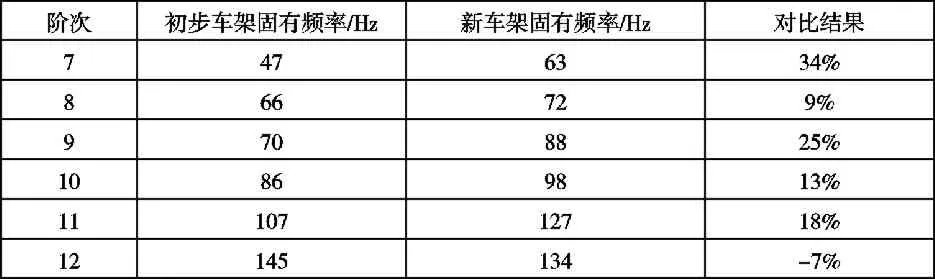
表4　车架固有频率对比表Tab.4 Contrast the natural frequency of the frame table

表5　车架刚度对比表Tab.4 Frame stiffness contrast table

图19　使用新车架的赛车Fig.19 Use the new frame of the racing car

经过对比后发现，在拓扑优化后的车架在低阶固有频率上得到了较多提升，在高阶固有频率上得到了略微下降，这非常有利于使车架避开地面带来的低频率响应与电机带来的高频率响应，从而避免发生共振[12]。在弯曲刚度与扭转刚度这两个评判车架力学性能指标上虽然有一些下降，但在轻量化上面得到显著提升。下图为赛车的实物图，车架得到了实际的检验。

5　结论

本文使用CATIA软件以及Hyperworks软件对FASE方程式赛车车架进行设计、分析、优化，最终加工出来的车架经过比赛的考验得到了实际的验证，得到了以下结论：

（1）车架前期设计很重要，合理的初步设计有利于提高拓扑优化结果的准确性。

（2）经过拓扑优化后，车架质量从40Kg降低为30Kg，提升了赛车整体性能，保证了赛车的操控稳定性。

（3）前五阶模态的结果相比于初始车架平均提升了20%，车架的安全性也得到了提升。引入尺寸优化等新设计方法将是本文今后的研究方向。

[1] 魏显坤,米林,万鑫铭,等.基于Optistruct的铝合金半挂车车架结构拓扑优化设计[J].四川兵工学报, 2012: 86-89.

[2] 陈垂福,蓝双,杨晓翔,等.基于SIMP理论的衡器载荷测量仪悬臂梁拓扑优化研究[J].机电工程, 2016: 383-387.

[3] 桂良进,周长路,范子杰.某型载货车车架结构轻量化设计[J].汽车工程, 2003: 403-406.

[4] 齐益强,周冠男,李涵武.FSAE竞赛车车架有限元静力学分析[J].黑龙江科技信息, 2013: 55-56.

[5] 赵帅,隰大帅,王世朝,等. FSAE赛车车架的强度和刚度分析[J].计算机辅助工程, 2011: 53-56.

[6] 郑文杰,兰凤崇,陈吉清. FSAE赛车车架结构拓扑优化及轻量化设计研究[J].汽车工程学报, 2016: 35-42.

[7] 彭倩,韩锋钢,洪汉池,等. FSAE赛车车架刚度特性分析[J]. 厦门理工学院学报, 2014: 7-11.

[8] 陈志勇,史文库,沈志宏,等. 轻型客车车身车架整体结构有限元模态分析[J].振动与冲击, 2010: 244-246, 263.

[9] 范文杰,范子杰,苏瑞意. 汽车车架结构多目标拓扑优化方法研究[J].中国机械工程, 2008: 1505-1508.

[10] 于国飞,黄红武,吴俊辉. 基于有限元的FSAE赛车车架的强度及刚度计算与分析[J].厦门理工学院学报, 2009: 29-32.

[11] 高棱,潘锦强,谢楚森,等.基于 ANSYS的 FSAE车架模态分析与验证[J].煤矿机械, 2016: 172-174.

[12] 郭福森,洪汉池,陈志军,等.FSAE赛车车架灵敏度分析与轻量化设计[J].厦门理工学院学报, 2015: 7-12.