基于压缩感知的扩频信号统一捕获技术

王　凯，吴　斌，汪　勃

(北京跟踪与通信技术研究所，北京100094)

0　引言

为了应对航天测控领域不同的任务模式和应用场景，新的测控体制不断涌现[1]，由此对设备通用性、标准化和小型化要求越来越高。

扩频测控体制是我国当前主流的测控体制，直扩和跳频是其中常见的2种信号体制，它们之间存在一定的差异，采用现有的接收设备会存在一些问题。若采用独立接收设备，则平台搭载的设备载荷负担较重，可扩展性差，不利于航天领域的应用[2]；如采用软件重载接收设备，则信号体制每次改变，就需要重新加载软件，地面到星上的延时使得系统的实时性受到限制[3]。因此需研究统一接收体制，在接收信号的过程中对不同体制的信号只需调整参数，具有实时性好、通用性强的特点。

此外，测控体制存在信息保密性不足的隐患[4]，新提出的提高测控频段、扩频码速率等抗干扰方法都会不同程度地增大系统带宽，接收设备的采样成本、设计难度都会急剧增加。因此有必要研究一种能够有效降低信号采样速率、解决其高数据率的信号处理方法。

压缩感知[5](Compressed Sensing，CS)是新提出的一种信号采集与处理理论，它以信号稀疏表示为基础，提出了采样率由信号所包含的信息量决定，而不再受限于信号带宽[6]，这为缓解采样压力提供了全新的途径。并且基于压缩感知理论的信号处理方法能用不同的稀疏矩阵和观测矩阵对不同体制的信号进行表达，为实现信号统一接收提供了可能。

本文利用压缩感知原理的内在联系，构建了基于压缩感知的直扩、跳频统一捕获接收框架，实现过程运用复用、优化的设计思路，节省了逻辑资源，降低了算法复杂度。仿真分析表明，提出的方法能有效捕获直扩、跳频信号，成功率高、模式切换速度快，相较于软件重载的捕获方法，在实时性上具有更好的性能。

1　压缩感知基本原理

压缩感知以稀疏表示理论为基础，通过对信号进行随机投影实现压缩采样，然后由采样值通过求解一个优化问题重构出原信号。其数学描述如下[7]：

设信号x∈RN在稀疏基Ψ下是K稀疏的，即

(1)

系数向量v中仅K个非零值，则可通过测量矩阵Φ投影完成压缩采样，获得低维测量值y：

y=Φx=ΦΨv=Θv，

(2)

式中，Φ∈RM×N为测量矩阵；Θ=ΦΨ为感知矩阵。然后可以通过优化算法由y恢复原信号x。由于感知矩阵Θ的行数M比列数N少，故式(1)是欠定方程，通常可以通过求解最小化l0范数问题来重构原信号[8]。

min‖v‖l0s.t.y=Θv。

(3)

当感知矩阵Θ满足约束等距特性时[9]，可以将式(3)等价地转换为式(4)所示的最小化l1范数问题。

min‖v‖l1s.t.y=Θv。

(4)

2　直扩信号CSPMF-FFT捕获算法

PMF-FFT捕获算法由于具备良好的性能而被广泛应用[10]，本文在PMF-FFT捕获算法的基础上，引入压缩感知思想，提出了CSPMF-FFT(Compressed Sensing PMF-FFT)捕获算法。

2.1　矩阵运算模型

为了便于引入压缩感知思想，首先建立PMF-FFT捕获算法的矩阵运算模型。根据PMF-FFT方法基本原理[11]，其捕获过程主要包括匹配滤波和傅里叶变换2个步骤。假设匹配滤波器个数为M，每个匹配滤波器对连续的X个码元进行相关，从而滤波器系数矩阵可表示为：

式中，ci为滤波器的抽头系数。每一次相关时刻，数据长度为N的信号不断滑入滤波器中，各次输入的信号可表示为X(假设L=N)：

Xi表示输入信号矩阵中第i列向量，即为每次滑动送入匹配滤波器的信号。完成匹配滤波后，将输出的M个相关结果做快速傅氏变换。M阶的离散傅氏变换基为PFFT，其中WM=e-j2π/M。

2.2　引入压缩感知思想

根据矩阵模型，可知完成一次PMF-FFT算法的运算过程可表示为θi=PFFTCPMFXi，将各次输出θi重新排列组成输出矩阵θ。由直扩信号的强自相关性可知，当捕获成功时，输出矩阵中会产生一个显著的峰值，而未完成捕获时输出值较小，由此可知信号经过变换在矩阵θ中呈现稀疏性。

根据上述分析，可以得到稀疏变换矩阵为：

Ψ=PFFTCPMF。

(5)

信号在此稀疏矩阵下的稀疏表示为：

θ=Ψx=PFFTCPMFx。

(6)

在稀疏表示后可利用测量矩阵完成压缩测量。随机高斯矩阵作为普适性的测量矩阵与稀疏矩阵具有良好的非相干性[12]，能有效地对信号进行压缩观测，得到信号的测量值：

y0=Φθ=ΦΨx，

(7)

式中，ΦM1×M为随机高斯矩阵。获得压缩测量值后，通过正交匹配追踪(OMP)算法对信号进行重构[13]，恢复稀疏系数矩阵θ，根据θ中峰值的位置索引可以估计得到码相位和多普勒频偏。

CSPMF-FFT算法在每一个码相位下进行搜索，捕获成功时输出信号矩阵中存在峰值且超过门限，记录相应的伪码相位并根据谱峰位置估计多普勒频移。当且仅当序列码相位完全对齐和频率完全补偿时，输出幅值最大。算法的捕获流程如图1所示。

图1　CSPMF-FFT捕获算法流程

3　跳频BDSA捕获算法

基于压缩域信号处理理论[14]，提出基于块对角稀疏分析(Block Diagonal Sparse Analysis，BDSA)的跳频信号捕获算法。

3.1　块对角稀疏分析

跳频信号在时频域具有显著的稀疏性，故其频谱在频率跳变处产生较大峰值[15]。但是信号在每一个时间段内只存在一个频率，直接采用傅里叶基只反映了其频域特性，而没有反映时域特性，即使能提取各频点的频率，也无法得到频点跳变顺序。故在捕获时需构造一个能同时反映其时、频域结构特点的稀疏矩阵。研究表明块对角稀疏矩阵能很好地表达跳频信号的时、频域特性，其结构如图2所示[16]。

图2　块对角矩阵结构

以仅包含2个频点的信号为例进行分析，依据可能出现的跳频频率和跳变时刻构建2个子对角块，即对k=1，2，...，N-1，构造k×k维傅里叶正交矩阵Ψk，1和(N-k)×(N-k)维傅里叶正交矩阵Ψk，2，并将矩阵Ψk，1和Ψk，2作为对角块构造稀疏矩阵Ψk：

构造Ψk时其子块矩阵维数有3种情况，如图3所示。无论是kK的情况，信号经稀疏变换后稀疏系数幅值均会发生峰值泄露，仅当k=K为跳频频点时，稀疏系数幅度的峰值达到最大，跳频信号才能在Ψk下进行最优稀疏分解[17]，如图4所示。

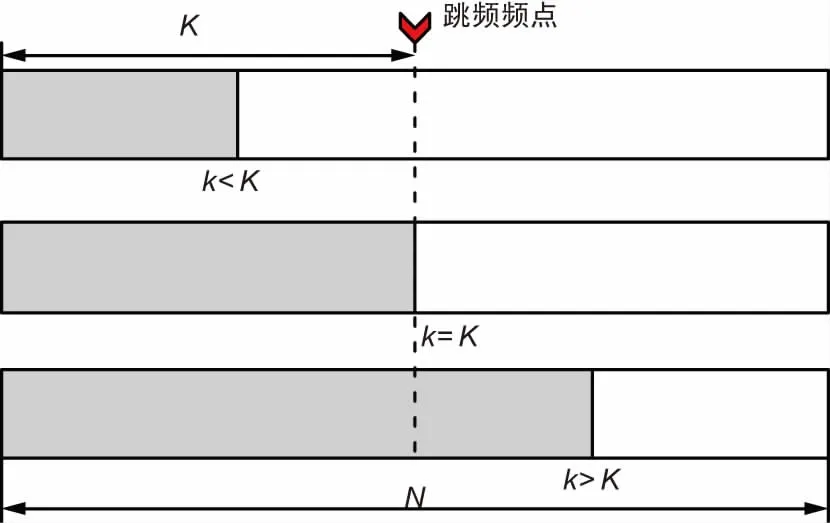
图3　块对角矩阵维数情况

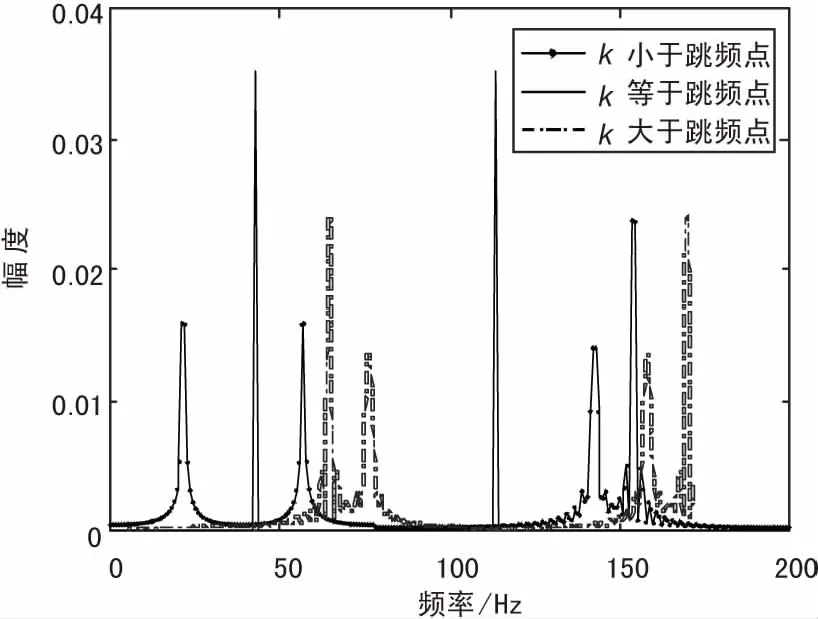
图4　不同矩阵情况下信号稀疏变换

3.2　引入压缩感知思想

首先用M×N维的高斯随机矩阵Φ对信号X进行压缩测量，获取测量值Y：

Y=ΦX=ΦΨkak=Θkak。

(8)

信号X在块对角稀疏矩阵Ψk下被表达为：

X=a1(K)×ΨK，P1(K)+a2(K)×ΨK，P2(K)，

(9)

式中，a1(K)和a2(K)为稀疏系数向量ak中存在的2个显著的非零系数；P1(k)和P2(k)为a1(K)和a2(K)在向量ak中的位置P2(k)。则压缩采样值Y可表示为：

Y=Θkak=a1(K)×θK，P1(K)+a2(K)×θK，P2(K)。

(10)

压缩测量值Y与感知矩阵Θk中的每一个列向量θk，i(i=1，2，3，...，N)进行相关运算，相应的表达式为：

(11)

当k≠K时，信号X在矩阵Ψk上不能完全稀疏表达，故得到的a1(K)和a2(K)相比k=K时小很多。因此可通过求解γ=α1(k)2+α2(k)2(k=1，2，3，...，N-1)的最大值估计参数K。

根据得到的跳变时刻K，通过P1(k)和P2(k)可以估计出信号中包含的2个频点频率f1和f2：

f1=(P1(k)-1)×fs/K，

(12)

f2=(P2(k)-K-1)×fs/(N-K)，

(13)

式中，fs=1/Ts为奈奎斯特采样率；N为一跳信号的采样点数。总结基于压缩感知的BDSA跳频信号参数估计算法的流程图如图5所示。

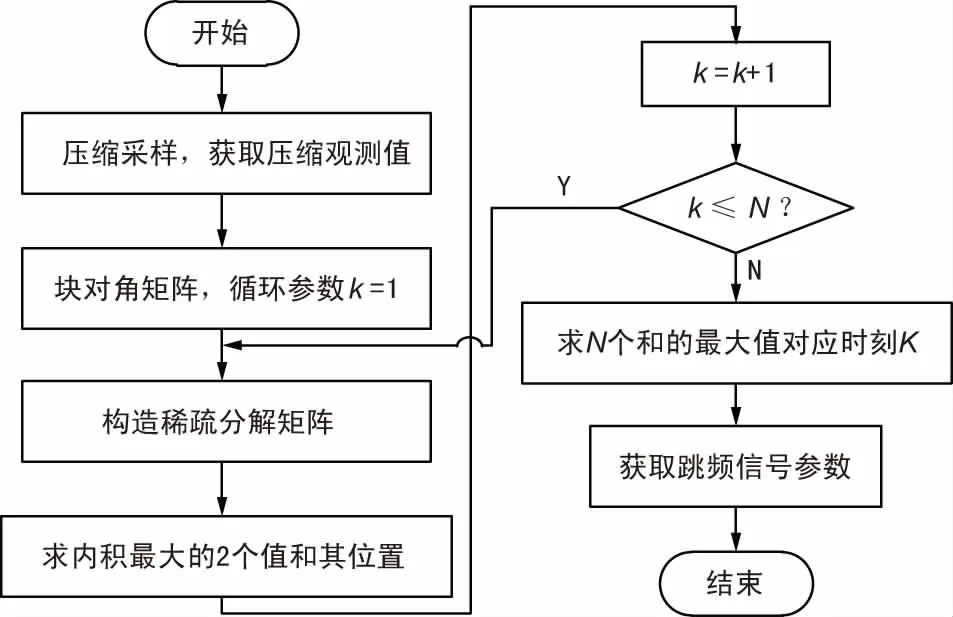
图5　BDSA捕获算法流程

4　统一捕获接收框架

基于压缩感知的扩频信号处理，能用不同的稀疏矩阵作为参数对不同体制信号稀疏表示，并辅以不同的测量矩阵进行压缩测量，最后通过重构算法或压缩域信号处理实现捕获。通过压缩感知理论的内在联系，搭建扩频信号统一接收框架，通过对不同体制信号的公共模块的提取，利用不同的参数实现同一模块的共用，完成对直扩和跳频2种体制信号的统一接收，统一接收框架如图6所示。

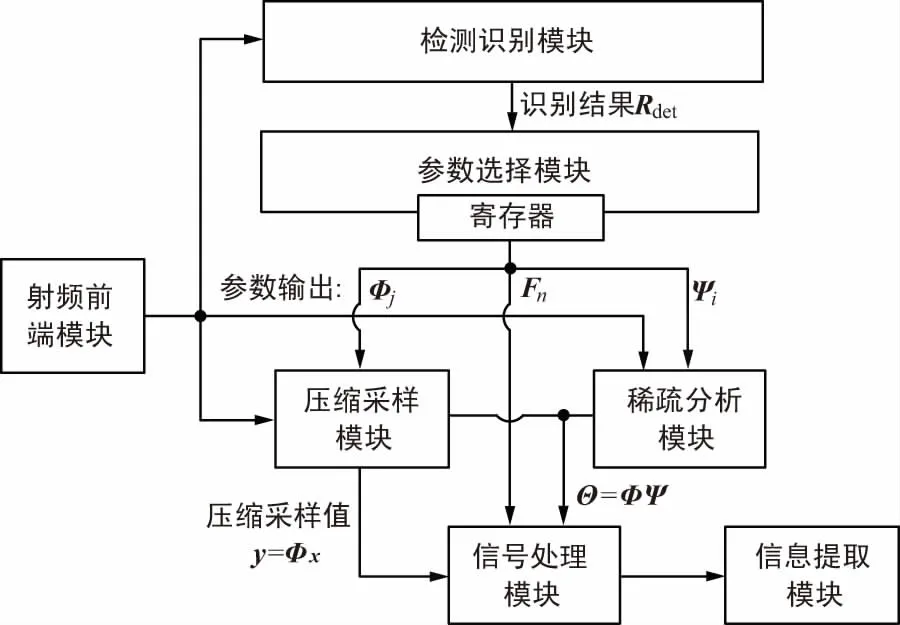
图6　基于压缩感知原理的扩频统一接收框架

由图6可知，扩频信号统一捕获框架主要包括：射频前端模块、检测识别模块、参数选择模块、压缩采样模块、稀疏分析模块、信号处理模块和信息提取模块。

在各模块中，压缩采样模块、稀疏分析模块和信号处理模块是基于压缩感知的统一捕获框架的核心组成部分。射频前端模块和信息提取模块是系统的前后端信号处理部分，为整系统的运行提供保障。检测识别模块和参数选择模块是多体制信号统一处理模块的必要组成部分，为整系统的顺利运行提供支撑。

确定统一接收系统中的各项参数，如表1所示。

表1扩频信号统一接收框架参数

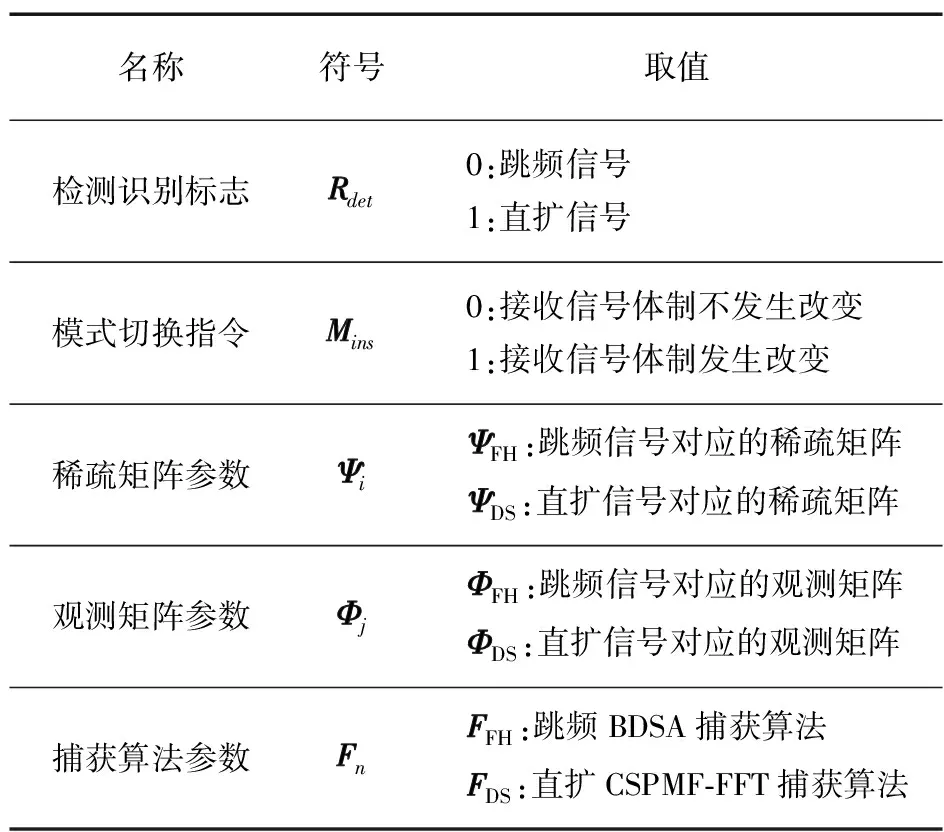
名称符号取值检测识别标志Rdet　0：跳频信号　1：直扩信号模式切换指令Mins　0：接收信号体制不发生改变　1：接收信号体制发生改变稀疏矩阵参数Ψi　ΨFH：跳频信号对应的稀疏矩阵　ΨDS：直扩信号对应的稀疏矩阵观测矩阵参数Φj　ΦFH：跳频信号对应的观测矩阵　ΦDS：直扩信号对应的观测矩阵捕获算法参数Fn　FFH：跳频BDSA捕获算法　FDS：直扩CSPMF⁃FFT捕获算法

基于统一捕获框架，设计统一捕获算法流程如下：

① 前端天线接收信号x，经前端模块处理后的信号被分别送入检测识别模块、压缩采样模块和稀疏分析模块。

② 检测识别模块调用检测识别算法，判断接收信号为跳频体制还是直扩体制，通过判决结果给Rdet赋值0或者1，并送入参数选择模块；模式切换指令Mins预置0表示接收体制不发生改变，当接收体制发生改变时设置为1。

③ 参数选择模块接收到检测识别符Rdet后，从寄存器中选择相应的稀疏矩阵Ψi送入稀疏分析模块，观测矩阵Φj送入压缩采样模块，捕获算法Fn送入信号处理模块。

④ 稀疏分析模块和压缩采样模块在接收到参数后启动工作，稀疏分析模块对信号进行稀疏分析提供理论先验：x=Ψv；压缩采样模块完成对接收信号x的压缩测量：y=Φx；完成后将压缩采样值y和感知矩阵Θ=ΦΨ送入信号处理模块。

⑤ 信号处理模块调用捕获算法Fn进行捕获处理，完成捕获并输出捕获信息，经信息提取模块处理后输出测距、测速等信息。

⑥ 当接到模式切换指令Mins时，重复步骤①～⑤；当不再有数据输入时，停止工作。通过模式切换指令的调度，当信号体制不发生改变时可以节省参数加载时间。

5　仿真分析与实验

5.1　CSPMF-FFT直扩捕获算法仿真分析

对提出的CSPMF-FFT算法进行仿真验证。考虑BPSK调制的扩频信号，载频4 MHz，码长1 023，信息速率1 kB/s，码速率Rc=10.23 Mc/s，码周期1/Rc，每个码元采集2个点，即采样率fs=2Rc，相关处理时间为1 ms。仿真中频偏设为8 500 Hz，伪码相位延迟为275，匹配滤波器个数M=64，每个滤波器相关积分码元数X=16，输出做256点FFT运算。

在压缩比为2的情况下，采用CSPMF-FFT算法对信号进行捕获，重构恢复得到离散输出谱峰如图7所示，对离散普峰值做曲线拟合，估得多普勒频偏为8 750 Hz，此时多普勒频偏分辨率Δfd=1/(MXTc)为250 Hz。匹配滤波相关输出幅值如图8所示，在码元相位为275成功捕获时产生一个显著的峰值。可见CSPMF-FFT算法能有效地捕获直扩信号并估计出信号的相位信息和多普勒频偏。

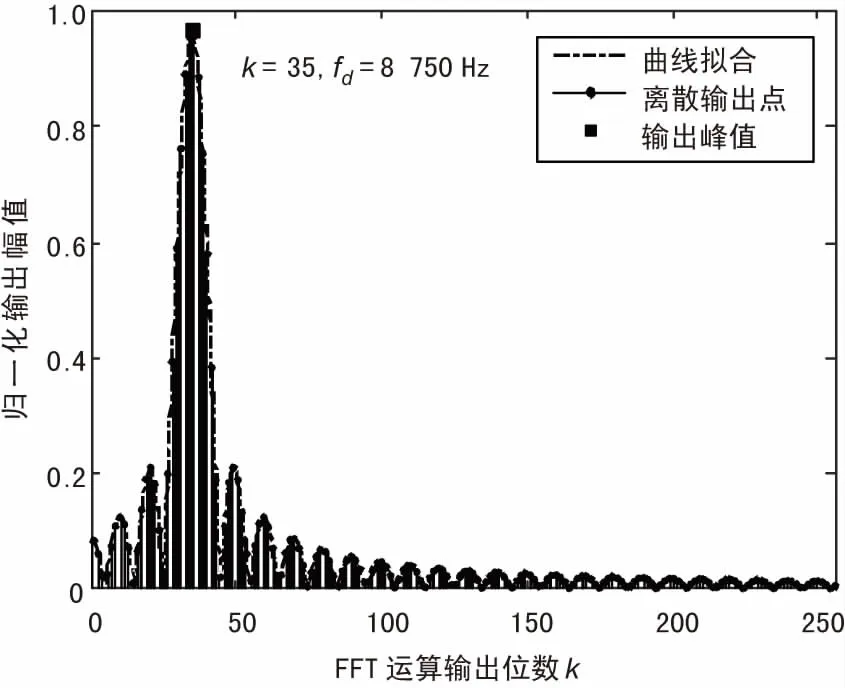
图7　离散重构谱峰与FFT变换位数关系

图8　相关输出幅度随码相位变换关系

在不同的信噪比和压缩比情况下，对CSPMF-FFT方法的捕获概率进行仿真，结果如图9所示。可见捕获概率随着信噪比的提高而上升，随着压缩比的提高而下降。在压缩比等于2的情况下，当信噪比大于-10 dB时捕获成功率达到90%以上，可认为CSPMF-FFT算法能有效地捕获直扩信号。

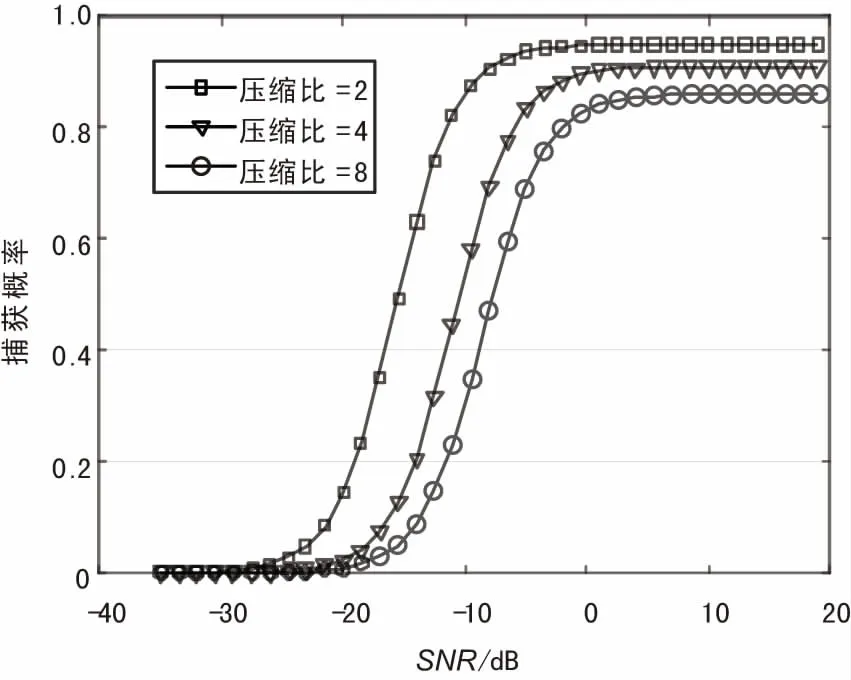
图9　直扩信号捕获概率

5.2　BDSA跳频捕获算法仿真分析

对BDSA跳频信号捕获算法的性能进行仿真分析，本质上是分析捕获算法对跳频频点和跳变时刻这2个参数的估计性能。设置跳频信号的仿真参数为：跳频点为{1.0，1.1，1.2，1.3，1.4，1.5，1.6，1.7} kHz，载波频率随机变化；跳频周期为200 ms，采样频率fc=4 kHz。在不同的信号信噪比下，考虑不同的压缩比，对参数进行估计，跳变时刻的估计成功率与跳变时刻的捕获成功率如图10和图11所示。

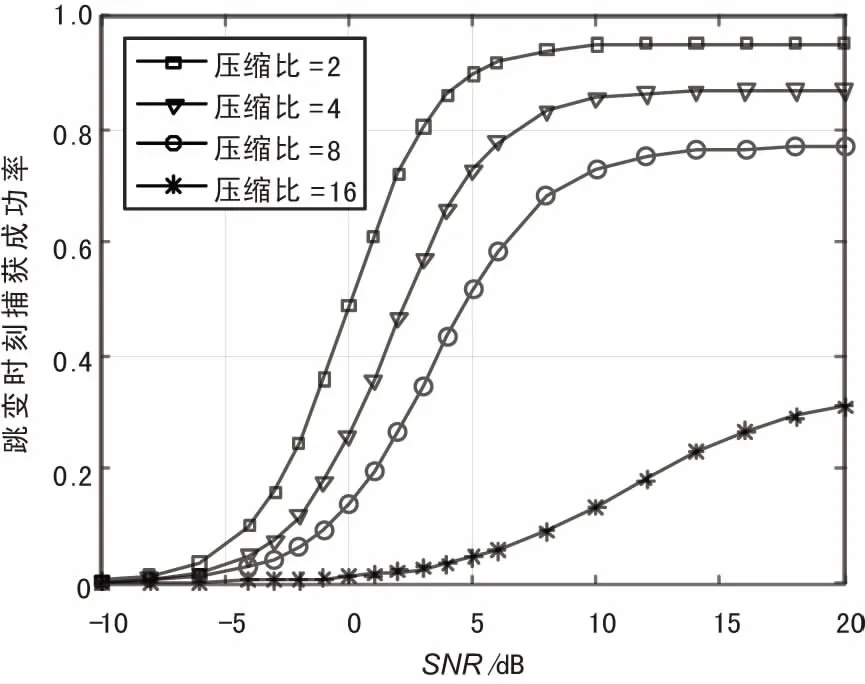
图10　跳变时刻捕获成功率

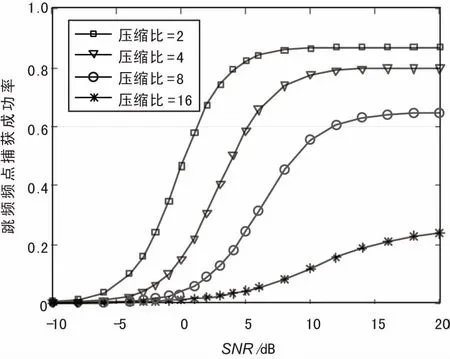
图11　跳频频点捕获成功率

图10和图11的仿真结果显示，对跳变时刻和跳频频点的捕获概率随信噪比的提高而上升，而当信噪比增大到一定程度时，捕获成功率维持在一个稳定值而不再继续上升。在信噪比相同的情况下，捕获概率随着压缩比的增大而下降。在压缩比为2、信噪比大于5 dB时，对跳变时刻的捕获成功率达到90%以上，对跳频频点的捕获成功率达到80%以上，此时能对跳变时刻和跳频频点有效地进行估计。当压缩比达到16时，捕获算法失效。相较于对跳变时刻的估计，在相同的信噪比与压缩比条件下对跳频频点估计概率较低，这是由于对频点的估计是建立在跳变时刻正确估计的基础之上，相应的捕获性能也因此有所下降。

5.3　统一捕获框架仿真分析

对扩频信号统一捕获接收框架进行仿真验证，系统的有效性和实时性是衡量其工作状况的2个重要指标，前面已经对捕获算法的有效性进行了分析，故此处主要针对实时性展开分析。

统一捕获系统实时性主要体现为不同体制模式切换时的实时性和对信号进行捕获的实时性。设定模式切换下直扩信号捕获工作模式和跳频信号捕获工作模式，分别记录下二者模式切换加信号捕获的总时间，与软件重载模式下对2种信号捕获的时间进行对比。

① 直扩信号实时性验证示意图如图12所示。直扩信号捕获工作模式，记录模式切换开始工作的时刻tDS1，生成直扩信号并对其进行捕获，记录捕获完成的时间tDS2，则工作模式切换加上直扩捕获的总时间为：

ΔtDS=tDS2-tDS1。

(14)

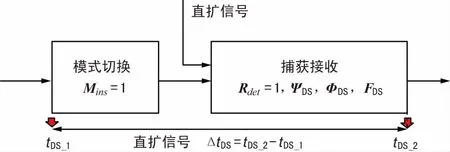
图12　直扩信号实时性验证示意

② 跳频信号实时性验证示意图如图13所示。跳频信号捕获工作模式，记录模式切换开始工作的时刻tFH1，生成跳频信号并对其进行捕获，记录捕获完成的时间tFH2，则工作模式切换和跳频信号捕获的总时间为：

ΔtFH=tFH2-tFH1。

(15)

图13　跳频信号实时性验证示意

③ 软件重载信号捕获仿真验证示意图如图14所示。软件重载信号捕获工作模式，作为对比，加入基于软件重载的捕获接收过程，此处仅考虑仿真软件重载程序，并未考虑设备间程序加注所需的信息传输、设备启闭等其他时间。记录完成上一次捕获的时间tall1，然后通过仿真软件重载程序，首先生成直扩信号并对其进行捕获，然后再重载一次程序，生成跳频信号并对其进行捕获，记录捕获完成的时间tall2，则该工作模式完成软件重载和2种信号捕获的总时间为：

Δtall=tall2-tall1。

(16)

图14　软件重载信号捕获仿真验证示意

将模式切换捕获时长ΔtDS和ΔtFH作为捕获框架实时性的验证指标，Δtall作为对照，利用仿真软件独立重复进行10次实验，由于耗时较小，因此每次实验重复进行5次模式切换及捕获过程，测取时长的平均值以克服随机性带来的偏差，对比结果如表2所示。

表2统一捕获与软件重载捕获耗时对比结果

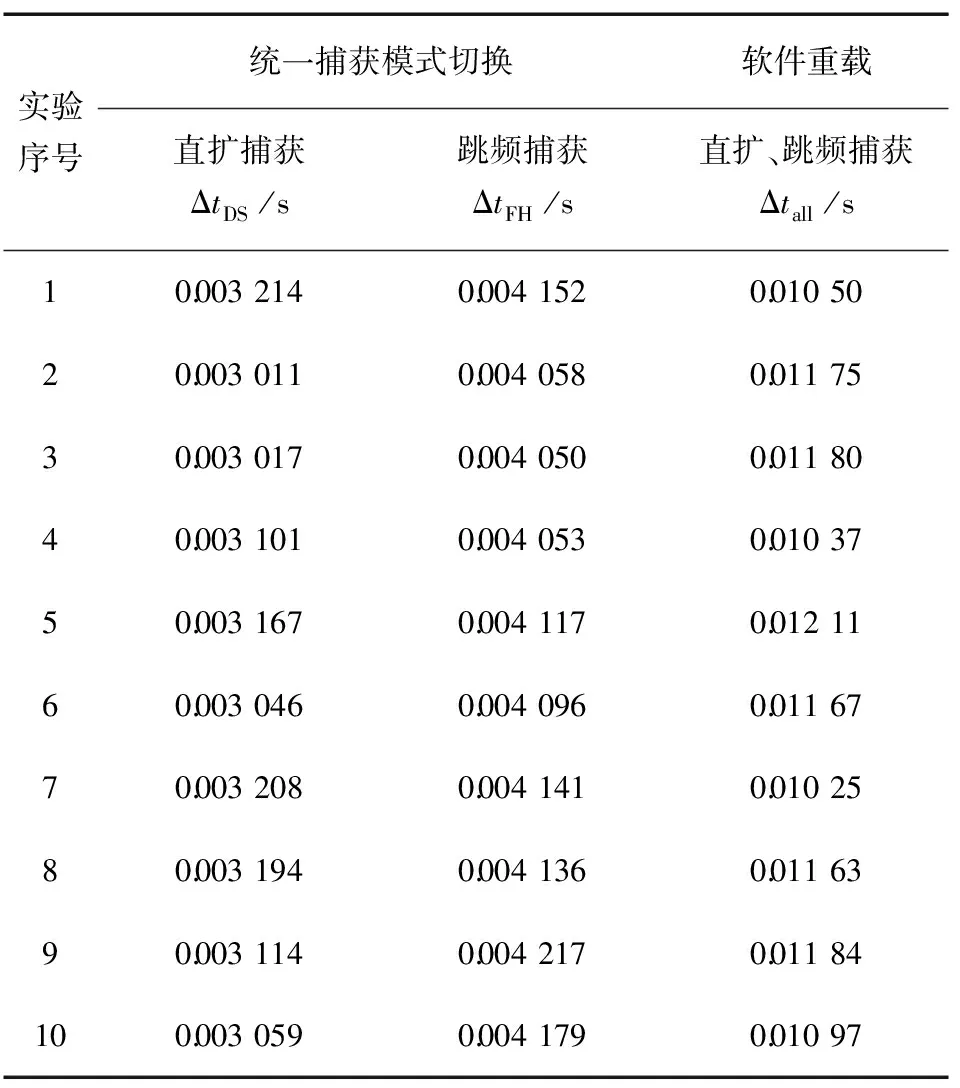
实验序号统一捕获模式切换软件重载直扩捕获ΔtDS/s跳频捕获ΔtFH/s直扩、跳频捕获Δtall/s10．0032140．0041520．0105020．0030110．0040580．0117530．0030170．0040500．0118040．0031010．0040530．0103750．0031670．0041170．0121160．0030460．0040960．0116770．0032080．0041410．0102580．0031940．0041360．0116390．0031140．0042170．01184100．0030590．0041790．01097

仿真实验结果表明，捕获系统对2种体制的信号能以小于0.005 s的时间完成模式切换及信号捕获，从而验证了捕获框架的实时性。并且相较于软件重载的捕获方法，完成2种信号捕获的时间总和小于软件重载完成2种信号捕获的时间，并且这是在未考虑设备间程序加注所需的信息传输、设备启闭等其他时间的情况下完成的，可见提出的统一捕获框架在实时性上具有更加优异的性能。

6　结束语

针对当前航天测控领域多体制信号捕获时接收设备存在的设备载荷负担重、采样压力大和实时性受限等问题，本文在对直扩、跳频压缩感知捕获算法分别进行研究的基础上，提取了信号稀疏分析、压缩观测和信号捕获的共用模块并进行了合理的复用与优化，构建了基于压缩感知原理的扩频统一捕获框架。仿真结果表明，提出统一接收框架能有效地对扩频信号进行捕获接收，在对信号捕获实时性上相较于软件重载的捕获方法具有更好的性能。全文通过对以上内容的研究，将新颖的压缩感知思想引入到扩频信号捕获接收技术研究中，不仅为解决当前扩频测控通信系统面临的问题提供了思路，也将为其未来的发展带来启发。研究成果能为测控设备小型化和信号处理任务的时效性带来帮助，对于资源受限、分秒必争的航天领域，将产生重大的影响。

[1]刘嘉兴.飞行器测控与信息传输技术[M].北京：国防工业出版社，2015：13-20.

[2]王远，姚艳军，王烁.我国天基信息网未来发展设想[J].信息通信，2014(1)：91-92.

[3]李志刚，张彧，潘长勇，等.抗单粒子翻转的可重构卫星通信系统[J].宇航学报，2009，30(5)：1752-1756.

[4]黄慈宁.测控通信非常规抗跟踪干扰方法研究[D].西安：西安电子科技大学，2015.

[5]DONOHO D L.Compressed Sensing[J].IEEE Transactions on Information Theory，2006，52(4)：1289-1306.

[6]HAYASHI K，NAGAHARA M，TANAKA T.A User’s Guide to Compressed Sensing for Communications Systems[J].Ieice Transactions on Communications，2013，E96-B(3)：685-712.

[7]BOUGHER B.Introduction to Compressed Sensing[J].Leading Edge，2015，34(10)：1256-1257.

[8]CANDES E J，ROMBERG J，TAO T.Robust Uncertainty Principles：Exact Signal Reconstruction from Highly Incomplete Frequency Information[J].Information Theory IEEE Transactions on，2006，52(2)：489-509.

[9]BARANIUK R，DAVENPORT M，DEVORE R，et al.A Simple Proof of the Restricted Isometry Property for Random Matrices[J].Constructive Approximation，2008，28(3)：253-263.

[10] 杨秦彪，王祖林，黄勤，等.高动态链路中折叠PMF-FFT快速捕获方法[J].系统工程与电子技术，2016，38(8)：1723-1729.

[11] QI J，LUO F，SONG Q.Fast Acquisition Method of Navigation Receiver Based on Folded PMF-FFT[C]∥Computing，Communications and It Applications Conference，IEEE，2015：62-66.

[12] 王侠，王开，王青云，等.压缩感知中的确定性随机观测矩阵构造[J].信号处理，2014，30(4)：436-442.

[13] JIAN W，KWON S，SHIM B.Generalized Orthogonal Matching Pursuit[J].IEEE Transactions on Signal Processing，2011，60(12)：6202-6216.

[14] 程艳合，杨文革，屈文星，等.压缩域直扩测控通信信号载波同步技术[J].电讯技术，2015，55(6)：585-593.

[15] 张益东，杨文革.基于压缩感知的跳频信号接收处理方法综述[J].通信技术，2016，49(4)：383-390.

[16] 邱砚驰.基于压缩感知的跳频信号盲处理系统的设计与实现[D].西安：西安电子科技大学，2015.

[17] 张春磊，李立春，王大鸣.压缩域宽带跳频信号跳变时刻估计算法[J].太赫兹科学与电子信息学报，2015，13(1)：122-129.