求解最短路问题的改进禁忌搜索算法

程　航，张　磊

(1.兰州交通大学 交通运输学院，甘肃 兰州 730070；2.中国港湾工程有限责任公司，北京 100027)

禁忌搜索算法Tabu Search是一种成熟的智能优化算法，该算法最初是一种局部搜索技术，算法原理为：通过模拟人类记忆能力，在搜索过程中防止陷入某一个最优解，设计禁忌表将其禁忌，为防止迭代过程中将最优解禁忌不能正常找到，故又加入了特赦规则，使得某些局部较优的解在加入禁忌表之后，又能够被“特赦”不至丢失，从而找到问题的全局最优解。禁忌搜索算法在线性与非线性问题中大量使用，尤其是在问题规模较为庞大、传统优化方法不能在较短时间内求得问题的最优解，禁忌搜索算法的优势更加明显。禁忌搜索算法有非常丰富的应用场景，以其广泛的适应性在工程优化问题中得到了大量使用。余丽等[1]，将禁忌搜索算法与遗传算法相结合，求解旅行商路径优化问题，并通过实际案例和不同规模的网络节点验证得到很好的效果。李进等[2]，将车辆路径问题使用禁忌搜索算法解决，该路径算法结合了一种路径编码与WSS解码算法，采用了3种邻域搜索策略，对节能减排的路径问题进行求解。宋晓宇等[3]，对解决Job Shop调度问题的禁忌搜索求解算法进行改进，主要体现在对邻域解的构造上，利用多点搜索，将搜索速度提到了新水平，最后将该算法应用到benchmarks问题上，得到的结果都较为满意。

最短路径问题是图论学中的经典问题，其问题基本描述是从网络中某一顶点出发，在网络(或图)中寻求一条路径使得该点到达终点的路径时间、距离或费用等加和最短(少)。最短路径问题以其丰富的变化，在诸多方面得到了应用，如城市网络规划、道路交通诱导系统、网络节点路由、网络布线、厂区选址等。曹旭等[4]，将旅游线路径的优化设计问题归结为最短路问题，并使用Floyd算法进行求解，选择甘肃及周边旅游景点作为案例，求得了从任意景点出发到下一个任意景点的最短路径。颜佑启等[5]，将基于最短路的交通流分配方法与公路最大流结合，给出了基于最短路的最大流交通分配计算方法，从而确定更加合理的公路网各路段交通量。

本文在对最短路问题建模分析的基础上，对最短路径问题提出一种改进禁忌搜索算法，给出算法实现的关键步骤及流程，并用案例验证提出的算法与传统的Dijkstra，比较计算结果验证该算法的可靠性。

1　网络定义

网络G(N,A)，其中N{n1，n2，…，nn}表示顶点集合，A{a1，a2，…，am}表示弧的集合。邻接点表示为

2　最短路径问题(Short-Path Problem)的数学模型

假设网络G，若i，j为G中的两个顶点，那么，i到j的最短路径数学模型可表示为

1)目标函数

.

(1)

式中：wij为顶点i到顶点j的权值，可表示时间、距离等；xij为最优路径是否经过弧Aij。

2)模型约束

(2)

(3)

3　禁忌搜索算法求解

3.1　基于顶点优先权的最短路径关键设计[6～14]

3.1.1编码及初始解的构造

本文采用实数编码方式，即给每个顶点一个优先权值，不考虑唯一性，使用随机数生成器Random()产生0～10的随机数，得到优先权数组weights，其中的weights(i)为顶点权重。从顶点1出发找到网络中优先权的最大顶点i*，将它加入到路径中，重复若干次，直到最后一个顶点n加入。即得到1～n的一条路径。

3.1.2邻域解的变化

禁忌搜索算法的迭代过程就是不断地从当前解出发找到邻域中的其他解，邻域解的产生过程就是解的变化，也叫邻域变化。本文考虑从路径的顶点s出发，找到顶点优先权最大且不在路径中的顶点，加入路径然后继续搜索，直到找到顶点t，计算该路径的总长度，同理再找到4条路径，比较得出当前最短路径。邻域解就是对换各个顶点的优先权，然后重新搜索。

3.1.3评价函数

从前面的说明可以发现，当一条路径确定后，该路径对应的距离L就能确定，所以本文采用目标函数为其评价函数。

3.1.4禁忌规则、禁忌长度、终止规则和特赦规则

1)禁忌对象：禁忌对象的选取有助于算法跳出局部最优解，本文将2-opt中的解作为禁忌对象。

2)禁忌规则：当某一个解z是N(z)当前的局部最优解(较优解)时，首先判断是否在禁忌表中。如果是，则选择次优解继续判断是否在禁忌表中；如果否，则将其作为本次迭代的局部最优解，再将z禁忌加入到禁忌表中。

3)禁忌长度：禁忌长度就是被禁忌的对象不被允许选取的迭代步数。 本文取禁忌长度为一个常数，其值应根据问题的规模大小而确定。

4)候选集合的确定：本文将从当前解的邻域中选择顶点优先权最大的若干个邻居作为候选集合。

5)终止准则：本文采用最大迭代步数作为算法的终止准则。

6)特赦规则：在算法迭代产生解的同时，记录该解的评价函数值和出现次数。当某一个解较优且优于当前问题的最优解时，将其从禁忌表中特赦。

3.2　禁忌搜索算法步骤

禁忌搜索算法寻优过程的实现得益于领域解的产生和候选解的选择等一系列步骤，表1是对算法具体实施步骤及关键技术实现的详细说明。

3.3　算法流程图

改进的禁忌搜索算法求解最短路径问题的关键：定义算法在何种情况下进行何种操作，如：算法在选择到较优解后应该先判断是否满足禁忌规则，如果不满足则将其作为候选解，并加入禁忌表；如果满足则进行下一步判断，看是否满足特赦规则等。具体流程如图1所示。

表1　算法步骤

图1　改进禁忌搜索算法的流程图

4　算例分析

4.1　初始化

本文以求解顶点数(规模)为30的网络最短路问题为算例(即找到一条路径，使得从顶点1到顶点30路径距离最短)，其中网络使用随机数产生。随机产生一个一维n列的向量weights作为顶点的优先权值，表2是将设置问题的规模设为n=10，利用随机发生器随机产生网络的不同边权和顶点优先权。那么，其具体初始化结果如表2所示。

表2　问题初始化举例

4.2　实验结果

本文使用C#语言编写，并实现了该算法，分别采用本文提出的算法和Dijkstra算法进行求解，结果如下：

两者均得到最优路径序列：12824252122232930；

最优解为80；

改进禁忌搜索算法迭代到179次时，收敛到最优解。

将两种算法求解过程中，最优解随算法迭代时间长度的变化情况叠加，得到如图2所示的结果。可以发现两种算法都逐渐收敛到问题的最优解，但传统Dijkstra算法的收敛速度较慢，最优解下落过程缓慢且初值较改进的禁忌搜索算法初值优化程度较差。而改进后的禁忌搜索算法较传统的Dijkstra算法，却有初始解较优、求解速度快等优势。

图2　两种算法比较

在对本算例使用两种算法计算结束后，可清楚地得到问题最优解、计算耗时等关键信息，具体如表3所示。

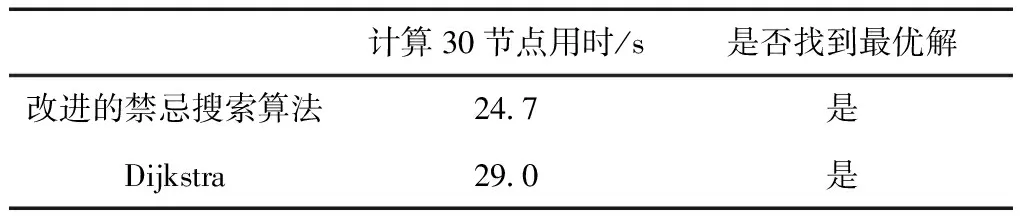
表3　计算结果对比

5　结　论

1)本文在对最短路问题简单描述的基础上，给出了问题的数学模型，基于顶点的优先权，构造初始解，进而优先权构造当前最优解的邻域，设计一种求解最短路径问题的禁忌搜索算法。

2)通过算例演算，上述计算结果表明，使用本文提出的改进禁忌搜索算法求解最短路问题的优势有两方面：一是可以求得问题的全局最优解(满意解)，二是该算法收敛速度较迅速，计算效率高。由此，可以证明本文提出的改进禁忌搜索算法的优化效果较好。

3)最短路径问题目前被广泛应用到路径导航、物流配送、交通诱导系统和无人驾驶等当下热点领域。仔细研究便会发现这些领域的研究要求时效性强，能够快速的给出并反馈运输方案结果[15-16]。本文对禁忌搜索算法的改进正是基于时间限制下要求快速求解这一要求提出的，通过不断优化算法参数(禁忌表长度、终止规则等)来降低算法求解的时间复杂度。

4)本文可以进一步研究的内容：动态交通流分配[17]是目前交通运输工程学科的热点，也是较难解的问题。一般地，可以首先使用最短路径算法求解出最短路径、次短路径、次次短路径，然后通过惩罚系数的办法将绕远路加入到可行的分配路径中，解决这类问题将是开展下一步研究方向。

参考文献：

[1]余丽,陆锋,杨林.交通网络旅行商路径优化的遗传禁忌搜索算法[J].测绘学报,2014,43(11):1197-1203.

[2]李佳,刘天琪,李兴源，等.改进粒子群-禁忌搜索算法在多目标无功优化中的应用[J].电力自动化设备,2014,34(8):71-77.

[3]宋晓宇,孟秋宏,曹阳.求解Job Shop调度问题的改进禁忌搜索算法[J].系统工程与电子技术,2008(1):93-96.

[4]曹旭,张喆,马少仙.最短路问题在旅游线路优化中的应用[J].科技广场,2012(2):115-118.

[5]颜佑启,欧阳建湘.最短路—最大流交通分配法[J].中国公路学报,2005(4):91-95.

[6]许谷声， 陈逸群，王解先，等.结合交通信息的最佳路径搜索[J].测绘工程,1999,8(4)：44-47.

[7]唐钱龙， 李央.基于多时段动态交通分配模型设计[J].交通科技与经济，2010,12(1)：18-20.

[8]俞晶菁.有限经济批量排产和运送问题的禁忌搜索算法[J].交通科技与经济，2012,14(1)：96-99.

[9]张健，张力鑫.带软时间窗车辆路径问题及禁忌搜索算法[J].交通科技与经济，2010,12(6)：44-46.

[10] 李庆奎，吕志平，李昌贵.基于模糊理论的智能最优路径算法[J].测绘工程,2011，20(4):5-8.

[11] 邢文训,谢金星.现代优化计算方法[M].北京：清华大学出版社,1999.

[12] 贺一,刘光远.禁忌搜索算法求解旅行商问题研究[J].西南师范大学学报,2002(3):41-45

[13] 彭茂.一种求解 TSP 问题的改进禁忌搜索算法[J].计算技术与自动化，2012(1):78-81.

[14] 王凌.智能优化算法及其应用[M].北京：清华大学出版社,2001.

[15] 李引珍,何瑞春,郭耀煌,等.多目标网络相异路径的Pareto解及其遗传算法[J].系统工程学报,2008,23(3):264-268.

[16] 何瑞春,李引珍.最佳相异度相异最短路径的遗传算法[J].兰州交通大学学报,2005(3):116-119.

[17] 李引珍. 不确定环境下交通运输网络路径求解方法及应用研究[D].成都：西南交通大学,2005.