基于改进的非线性GM(1,1)模型的职业病预测研究*

杨　珊，明俊桦，周智勇

(中南大学 资源与安全工程学院，湖南 长沙 410083)

0　引言

据国际劳工组织(ILO)资料显示，全球范围每年有接近2百万人死于职业相关疾病。因职业伤害引起的世界经济损失达到2.8万亿美元，在全球各国国民生产总值中占据4%[1]。乔庆梅、徐金梅[2-3]指出，目前我国职业病状况不容小视，与职业病有关的相关参数都占全球第一。因此，职业病的预防形势相当严峻。朱进平、梅震[4]的研究表明，职业病具有迟发性和隐匿性，未来的病例数也会逐渐增加。关于职业病研究方面，国内外已有较多学者参与，相关研究成果也已在职业病预防措施中得到应用。例如：孙银铃、邵华等[5]指出，从整体上来说，中国在职业病防治方面的力度与美国有一定差距，还有很多工作要做；日本的恒川谦司[6]在了解中国职业卫生的现状基础上，结合日本的职业卫生措施，提出一系列建立、健全中国职业卫生管理的对策和建议。但是，针对全国范围内的职业病预测，现有研究尚有不足，灰色预测方法以其所需样本小、建模简单、精度高及实用性强等特点，得到广泛应用[7-8]。王维、李建东[9]使用经典GM(1,1)模型，对职业病分类进行了预测分析，相关预测准确度尚不够理想；李怡、张华东[10]虽然使用的是改进GM(1,1)模型，不过并没考虑到非线性关系；文献[11]和[12]提到了非线性GM(1,1)改进模型，其应用的领域分别是房地产价格指数预测以及“两税”税收预测，为本文提供了一定的理论基础，不过该方法的预测精度仍有提高空间；时冬青、宋文华等[13]提出灰色 GM(1,1)—马尔科夫模型，将其应用在职业病预测方面。在现有学者相关职业病预测方面的研究成果基础上，本文进一步完善和改进相关预测模型，提出改进的非线性GM(1,1)改进模型，为职业病发病趋势的预测提供理论和方法参考。

1　经典GM(1,1)模型

将原始数据记为序列X(0)=(x(0)(1),x(0)(2),…,x(0)(n)),经典GM(1,1)模型建模步骤如下：

1)步骤1，对原始序列X(0)做一次累加生成，得数据序列：

X(1)=(x(1)(1),x(1)(2),…,x(1)(n))

(1)

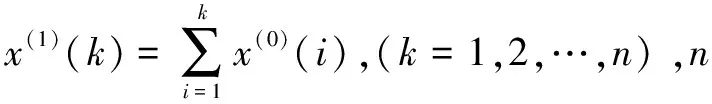
2)步骤2，建立GM(1,1)模型的基本形式，如式(2)所示：

x(0)(k)+az(1)(k)=b,k=1,2,…,n

(2)

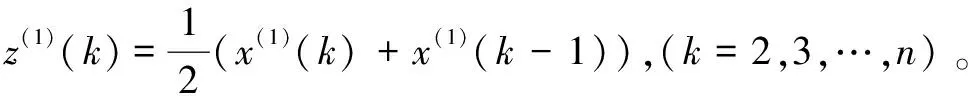
(3)

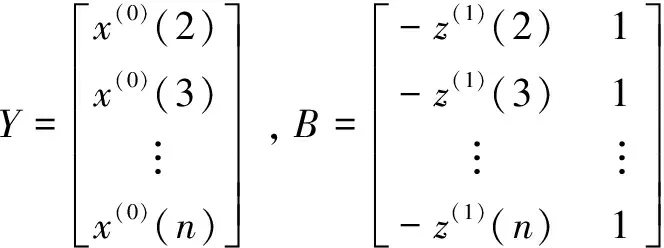
4)步骤4，模型(2)对应的白化方程或影子方程为：

(4)

由其解得时间响应函数：

(5)

取x(1)(1)=x(0)(1)，则模型(2)的时间响应序列为:

(6)

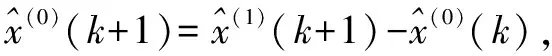
(7)

2　改进的非线性GM(1,1)模型

因国家政策、社会条件等因素的影响，历年实际职业病例数规律性相对较弱，其增减趋势不一，会出现陡增或陡减的现象，因此本文首先选用几何弱化算子理论对原始数据进行处理，使数据变得有规律可循，增强模型预测的准确度。

由式(2)可知，经典的GM(1,1)模型实质上是把{x(0)(k)}和{z(1)(k)}这2组数值之间看作线性关系进行求解参数的。但是，在实际计算过程中，{z(1)(k),x(0)(k)}的散点往往不在一条直线上，即不符合线性关系，若仍做线性关系进行处理，就会造成较大的误差。因此，改进模型将{z(1)(k),x(0)(k)}原本的线性假设，改为非线性假设进行处理，以提高曲线的拟合度。

为保证方程的可解性，本文将结合常用曲线(直线：y=a+bx；双曲线：1/y=a+b/x；幂函数曲线：y=b0xb1；指数函数曲线：y=b0eb1x；增长曲线：y=eb0+b1x)建立非线性方程，再比较各曲线的拟合度，找到最吻合的曲线关系，分析曲线参数，最终得到非线性GM(1,1)模型。相关分析步骤如下所示：

1)步骤1，利用几何平均弱化缓冲算子，对原始数据进行处理。设X(0)=(x(0)(1),x(0)(2),…,x(0)(n))为非负的系统行为数据序列，即x(0)(i)≥0。令

X(0)′ =X(0)D= (x(0)(1)d,x(0)(2)d,…,x(0)(n)d)

(8)

其中：

2)步骤2，分别将数据从上述曲线出发，建立非线性回归模型：

x(0)(k)=fi(z(1)(k),a,b)i=1,2,…,6

(9)

式中：a,b为未知参数。

3)步骤3，基于R2最大原则，确定最佳拟合曲线f(z(1)(k),a,b)。其中R2是表示各曲线与原始数据的拟合程度的参数，其数值越大，则代表曲线的模拟值和原始数值的差别越小，则该曲线的模拟效果越好。

4)步骤4，预测精度的检验，通过后验差比值C和小误差概率P，评判模型预测精度的合格与否[13],如表1所示，其计算公式分别为：

(10)

P=P{|ε(t)-ε| <0.674 5s1}

(11)

式中：s2为残差数列的标准差，s1为原始数列的标准差，ε(t)为残差数列，ε为残差数列均值。

3　应用实例

本文用我国职业病发病例数作为研究对象，验证该改进的非线性GM(1,1)模型的可靠性和准确性，使用2005—2014年的数据作为研究数据，资料来源于2005—2014年国家卫生和计划生育委员会(卫生部)发布的关于职业病防治情况的通报[13]，具体数据如表2所示。

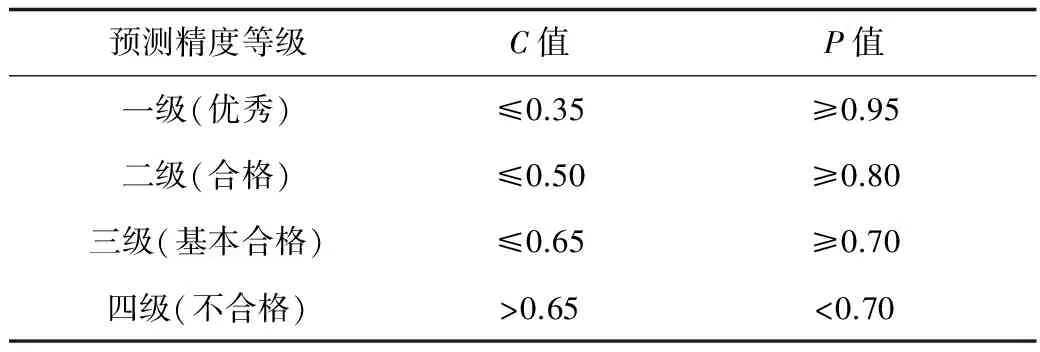
表1　后验差比值和小误差概率预测精度评判检验

表2　2005—2014年我国职业病发病例数统计

其中，2006年的职业病例数为29个省份的数据，其他年份均为30个省份的职业病数据，因此，为了使数据具有较高的参考性，本文利用“平均值比例差补法”[13]，以 2005 年的职业病发病例数作为依据，算出2006年的数据为11 805例。

3.1　传统GM(1,1)模型

以2005—2013年的9个职业病例数为建模数据进行处理。设：

X(0)=(x(0)(1),x(0)(2),x(0)(3),x(0)(4),x(0)(5)，x(0)(6)，x(0)(7)，x(0)(8)，x(0)(9))=(12 212.00,11 805.00,14 296.00,13 744.00,18 128.00,27 240.00,29 879.00,27 420.00,26 393.00)

采用传统GM(1,1)模型进行拟合，得到结果如表3所示。

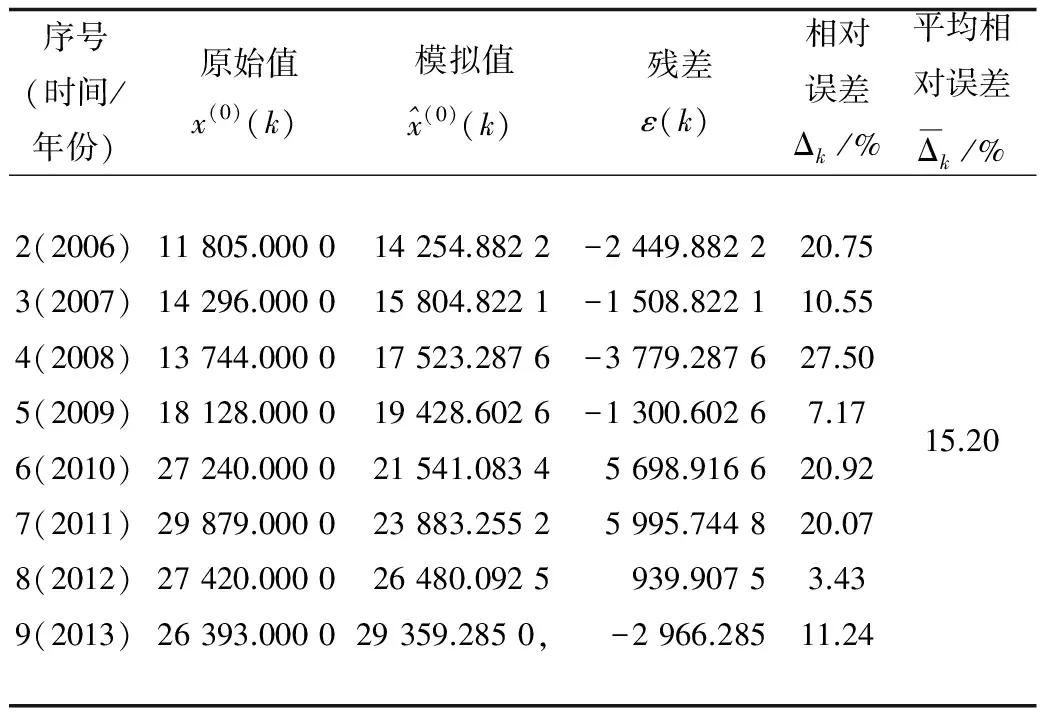
表3　传统GM(1,1)模型的建模拟合效果

由表3可以看出，传统GM(1,1)模型拟合的平均相对误差为15.20%，并预测得到2014年的职业病例数为32 552例，根据职业卫生网的数据，2014年的职业病例数为29 972例[13]，预测相对误差为8.61%。由此可知，该经典模型预测误差较大。

3.2　改进的非线性GM(1,1)模型

3.2.1几何平均弱化缓冲算子的应用

2005—2013年的数据并不是呈现稳定增长或减少的状态，会受到各种因素的影响而波动较大，特别是2010年的数据陡增。如果直接利用原始数据进行模型的构建，那么预测结果很大程度上不具备参考性。针对这个问题，灰色系统中提出了“灰色序列”，主要通过对原始数据的挖掘以及整理，重新发现数据之间的规律，进而构建数量关系模型。从表2可以看出，2010年的职业病的病例数陡增，因此采用几何平均弱化缓冲算子对原始数据进行处理，减缓其增长速度[14]。处理过程如下：由式(8)计算得到弱化值X(0)′ = (18 812.451 4,19 856.500 7, 21 462.816 2, 22 966.707 3,25 450.472 7, 27 703.353 4, 27 859.549 5, 26 901.599 6, 26 393.000 0)。

3.2.2改进的非线性GM(1,1)模型的建模

采用SPSS软件，选取几种常见的曲线模型进行分析，表4给出了各个曲线模型的拟合优度、模型检验结果和参数估计值。由R2最大原则，确定最佳拟合曲线。其中二次曲线模型的R2=0.966，该模型的拟合度最佳。几种曲线模型的拟合效果如图1所示，小圆圈代表原始观测记录，从直观上看，显然二次曲线和原始数据拟合的更好。

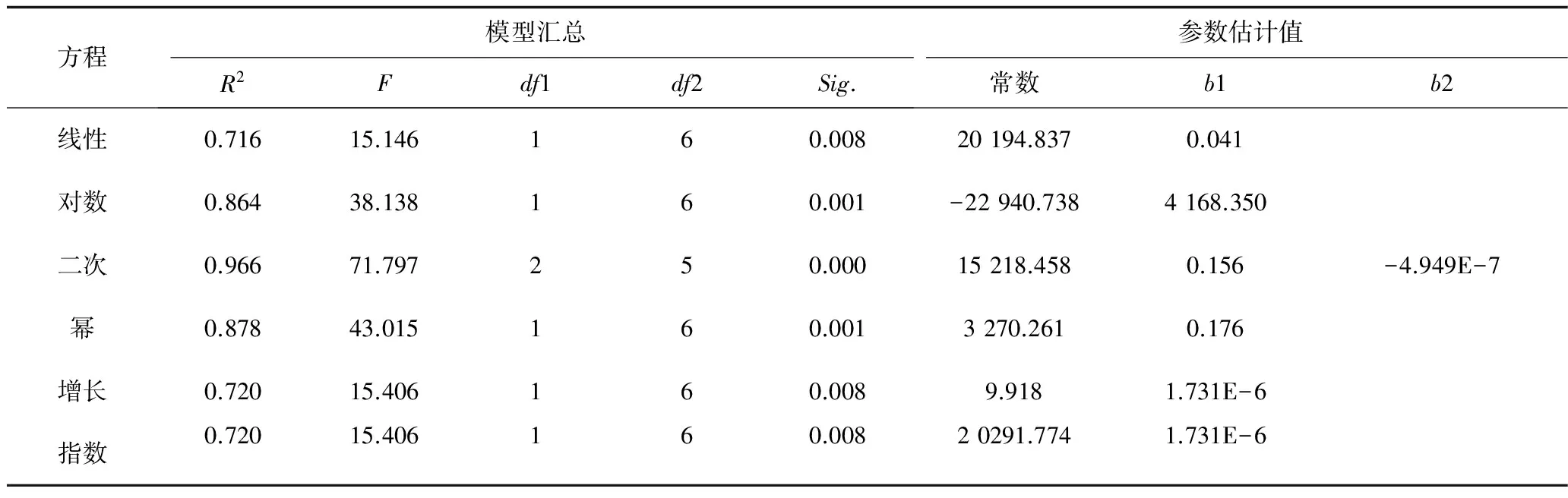
表4　常见曲线模型汇总和参数估计值

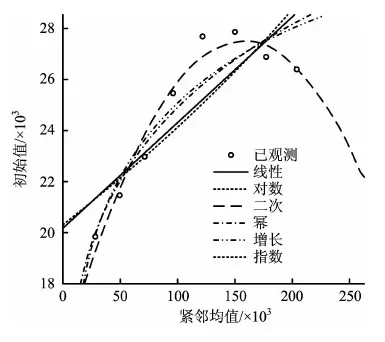
图1　常见曲线模型拟合效果Fig.1　Fitting effect of common curve model

二次曲线的方程设为：y=ax2+bx+c。以数列X(0)′作为因变量y值，而该数列的紧邻均值作为自变量x值，利用MATLAB计算出二次曲线的参数a，b，c，得到所求二次曲线的方程为：

y=-4.949×10-7x2+0.156x+15 218

(12)

将X(0)′的紧邻均值数列作为自变量带入式(12)中，可求得相应的因变量，即拟合值，详见表5所示。从表5可知，改进的非线性GM(1,1)模型的拟合值和原始值之间的平均相对误差为1.81%，低于传统GM(1,1)模型的平均相对误差。接着利用该模型，重复上述步骤重新建模，预测得到2014年的职业病例数为29 042例，根据职业卫生网的数据，2014年的职业病例数为29 972例，预测相对误差为3.10%，比经典GM(1,1)模型的预测精度高。

3.2.3拟合效果比较

利用后验差比值C和小误差概率P这2个参数指标来比较2种模型的预测精度，如表6所示。

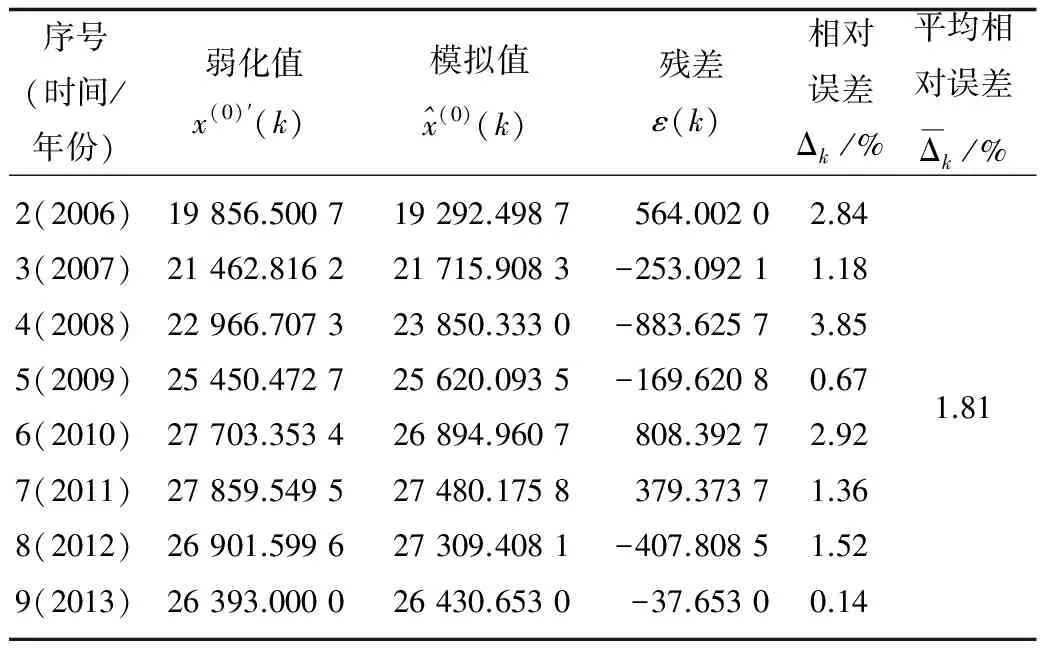
表5　改进的非线性GM(1,1)模型的建模拟合效果

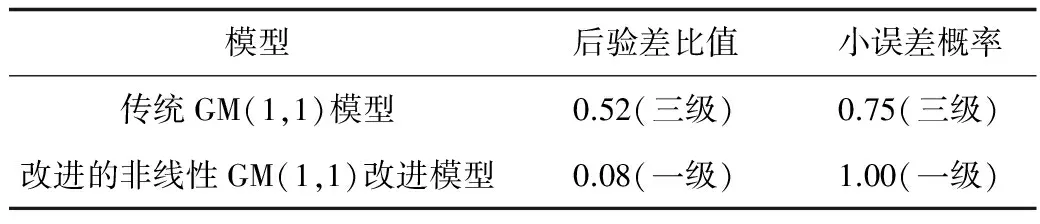
表6　2种模型的预测精度比较

从表6中可以看出，改进的非线性GM(1,1)模型的预测精度比传统GM(1,1)模型高，可为职业病预测以及职业卫生防治措施等工作提供更准确的参考和支持。

由表3和表5数据可分别得到传统GM(1,1)模型的拟合曲线效果图和经弱化处理的非线性GM(1,1)改进模型的拟合曲线效果图，如图2和图3所示。

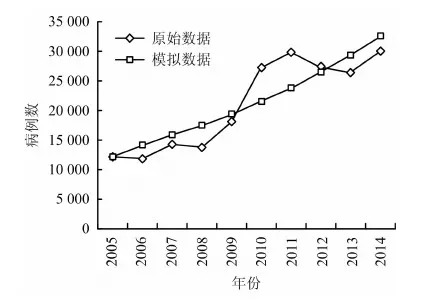
图2　传统GM(1,1)模型的拟合效果Fig.2　The fitting effect diagram of the traditional GM (1,1) model

图3　改进的非线性GM(1,1)模型的拟合效果Fig.3　The fitting effect diagram of the improved GM (1,1) model

由图2可看出，在传统GM(1,1)模型预测中，原始数据有较大的波动，而得到的模拟数据却是一条平滑曲线，并未体现出数据的变化特征；由图3可看出，改进的非线性GM(1,1)模型中的弱化数据和模拟数据基本一致，拟合度较高。可见，改进模型中引入的弱化理论和非线性假设，有效地解决了预测精度不高的问题，为职业病预测提供了有效的方法。根据改进的非线性GM(1,1)模型，进一步预测得到2015年的职业病病例数为34 900例。

4　结论

1)改进的非线性GM(1,1)模型中，利用几何平均弱化算子对原始数据进行处理，并将原始数据与紧邻均值之间线性假设变为非线性假设，使得该模型在职业病发病例数的预测精度上有了较大提高。

2)通过比较可知，相比传统模型的职业病预测平均相对误差15.20%，改进的非线性模型降低到了1.81%；以2014年为验证数据时，传统模型的相对误差为8.61%，而改进的非线性模型变为3.10%；在后验差比值和小概率误差检验时，传统模型的预测精度为三级，而改进的非线性模型提高到一级。

3)根据该改进的非线性GM(1,1)模型，得到2015年职业病的预测值为34 900例。

4)职业病的病例数会受到多种因素的影响，例如其本身所具有的“隐匿性”、“迟发性”等特点，各种诊断仪器及标准的更新，人们思想观念的转变等。以上因素在一定程度上，会影响该模型的预测精度，但职业病的总体趋势依旧在不断增长，我国仍需加强对职业病的防治力度，尽最大的努力保障最广大人们群众的身体健康。

5)今后职业病的预测将会越来越细化，即具体到每一种职业病的发病例数的预测，以便为我国职业病的防治工作提供更有力的支持。

[1]贾麟.全球职业安全健康问题与新形势[J].中国安全生产,2014(11):58-59.

JIA Lin.Global occupational safety and health issues and the new situation[J].China Occupational Safety and Health, 2014(11):58-59.

[2]乔庆梅, 柯常云. 我国职业病防治的现状与思考[J]. 中国医疗保险, 2011(12):59-62.

QIAO Qingmei,KE Changyun.The present situation of occupational disease prevention and cure in china and thoughts on it[J].China Health Insurance,2011(12):59-62.

[3]徐金梅．职业病防治现状分析及其对策[J]．西部探矿工程，2008，20(7)：239-241.

XU Jinmei.The actuality analysis and countermeasure of prevention and cure of industrial disease in China[J]. West-China Exploration Engineering,2008,20(7):239-241.

[4]朱进平，梅震．职业卫生监督量化分级管理模式探讨[J]．工业卫生与职业病，2008，34(6)：378-381.

ZHU Jinping,MEI Zhen.Discussion on quantitative classified management mode of occupational health supervision[J].Industrial Health and Occupational Diseases,2008,34(6):378-381.

[5]SUN Y, SHAO H, WANG H. Occupational diseases prevention and control in China: a comparison with the United States[J]. Journal of Public Health, 2015, 23(6):379-386.

[6]恒川谦司, 刘宝龙, 高建明,等. 日本职业卫生管理及对中国的启示[J]. 中国安全生产科学技术, 2008, 4(1):116-119.

TSUNEKAWA K, LIU Baolong, GAO Jianming，et al. Occupational health management in Japan and its enlightenment to China[J].Journal of Safety Science and Technology,2008,4(1):116-119.

[7]LIN Y, LIU S. An introduction to grey systems: foundations, methodology and applications[J]. Kybernetes, 2003, 32(4):584-585.

[8]刘思峰. 灰色系统理论及其应用(第五版)[M]. 北京：科学出版社, 2010.

[9]王维,李建东.GM(1,1)灰色模型在职业病发病预测中的应用[J].中国公共卫生管理,2014,30(6)：920-922.

WANG Wei，LI Jiandong. Application of GM(1,1) grey model in prediction of occupational disease[J]．Chinese Journal of Public Health Management,2014,30(6): 920-922．

[10]李怡，张华东．改良灰色模型在职业病发病趋势上预测的分析研究[J]．预防医学情报杂志，2015，31(8)：630-634.

LI Yi，ZHANG Huadong．Application of refined grey model in forecasting the of occupational disease[J].Journal of Preventive Medicine Information,2015,31(8): 630-634．

[11]钱峰, 吕效国, 朱帆. 灰色GM(1,1)模型的改进模型在房地产价格指数预测中的应用[J]. 数学的实践与认识, 2009, 39(7):29-33.

QIAN Feng,LYU Xiaoguo,ZHU Fan.The application of the improved grey GM (1,1) model in real estate price index prediction[J].Mathematics in Practice and Theory,2009,39(7):29-33.

[12]郭晓君，李大治，褚海鸥，等．基于GM(1,1)改进模型的“两税”税收预测研究[J]．统计与决策，2014(4)：34-36.

GUO Xioajun,LI Dazhi,CHU Haiou，et al. The study on the prediction of "Two Taxes" tax based on the improved GM(1,1) model[J].Statistics and Decision,2014(4):34-36.

[13]时冬青, 宋文华, 张桂钏,等. 基于灰色GM(1,1)-马尔科夫模型的职业病预测研究[J]. 中国安全生产科学技术, 2017, 13(4):176-180.

SHI Dongqing,SONG Wenhua,ZHANG Guichuan，et al.Study on prediction of occupational diseases based on grey GM(1,1)- markov model[J]. Journal of Safety Science and Technology, 2017,13(4)：176-180.

[14]陈昌源, 戴冉, 杨婷婷,等. 基于改进 GM(1,1)模型的上海港集装箱吞吐量预测[J]. 船海工程, 2016, 45(4):153-156.

CHEN Changyuan,DAI Ran,YANG Tingting, et al. Study on container throughput prediction of shanghai port based on improved GM(1,1) model[J].Ship & Ocean Engineerine, 2016, 45(4): 153-156.