Fe- Ti- C三元系热力学优化
王菲菲 鲁晓刚,2 潘 涛 苏 航
(1.上海大学 材料科学与工程学院,上海 200444;2.上海大学材料基因组工程研究院,上海 200444;3.钢铁研究总院工程用钢研究所,北京 100081)
近年来,异种金属连接复合板因其优异的综合性能,被广泛应用于机械、电力和化工等行业,需求量持续增加[1]。其中,由于钛合金在运输、发电和化学工业的日益广泛应用,且钛合金与碳钢及不锈钢层状金属复合材料拥有价格低廉、性能优越以及极高的性价比等优点,越来越多的学者对钛钢复合板进行了研究。
研究表明,异种金属扩散连接的工艺参数直接影响界面处的组织类型及扩散层厚度,而扩散过程是决定结合界面组织和性能的关键。如果可以建立元素扩散与界面组织之间的关系,就可以通过对原子扩散的模拟及计算预测界面组织,合理设计复合工艺。对于钛钢复合材料,其基本的合金元素为Fe、Ti和C,为了深入研究复合材料界面的组织演变规律,有必要研究不同温度及合金成分下三元系Fe- Ti- C的相平衡及原子扩散规律。本文利用CALPHAD方法同时结合第一性原理计算,对Fe- Ti- C三元系进行了热力学优化,为复合材料组织的模拟预测提供理论支持,进而优化设计复合材料的成形工艺。
1 理论方法及模型
1.1 热力学模型
本文采用Thermo- Calc软件进行热力学计算与优化[2]。其中,纯组元的Gibbs自由能来源于Dinsdale[3]。
液相Liquid用替换式溶液模型(Fe,Ti,C),其Gibbs自由能表达式为:
(1)
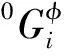
(2)
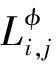
(3)
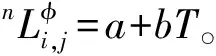
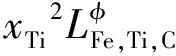
(4)
固态溶体相BCC_A2、FCC_A1和HCP_A3的Gibbs自由能用亚点阵模型(Fe,Ti)a(C,Va)b,其Gibbs自由能表达式为:
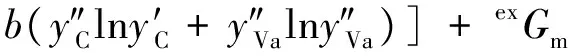
(6)
因为金属间化合物FeTi为有序相,B2结构,使用三个亚点阵模型(Fe,Ti,Va)0.5(Fe,Ti,Va)0.5(Va)3,其摩尔Gibbs自由能表达式为:
(8)
(10)
(11)
(12)
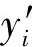
对于Laves相Fe2Ti,使用点阵比为2∶1的双亚点阵模型。同时,为了更好地拟合试验数据,采用第一性原理计算得到Fe2Ti相的端基自由能,其Gibbs自由能表达式为:
(13)
1.2 第一性原理计算
以量子力学为理论基础的第一性原理计算又称从头计算(abinitio calculations)的方法,在计算过程中不需要试验参数,直接从物质的本征参数入手,因而可以计算很多试验无法得到的数据且结果准确,指导意义强,在材料计算及材料设计领域得到了广泛应用。
第一性原理计算目前能够较准确地计算无序结构的能量,合金特殊准随机结构(Special Quasirandom Structures,SQS)就是其中的一种方法。本文采用16个原子的SQS模型和VASP软件对bcc相的形成焓进行了计算,并用VASP软件计算了Fe2Ti相的端基能量。
2 试验材料与方法
使用WK- II非自耗型真空熔炼炉在氩气保护下熔炼二元合金样品,具体合金成分见表1。原材料为纯度99.995%的钛和纯度99.995%的铁。为了得到均匀性良好的样品,所有样品均经过5次熔炼,并在1 423 K下进行一周的均匀化处理。将均匀化处理后的样品线切割成尺寸5 mm×5 mm×5 mm的锭样,经打磨后放入石英管中封真空。再对样品进行不同温度和时间的退火处理,具体工艺参数见表1。退火后取样进行镶嵌、打磨和抛光。最后使用JEOL JXA 8900 EPMA对样品的相组成进行分析,结果见表1。
3 结果与讨论
3.1 Fe- Ti二元系热力学优化
Bo Hong等[4]综述了Fe- Ti二元系的相关热力学试验信息。本文通过评估现有试验信息,重新优化了Fe- Ti二元系的热力学参数,优化结果如表2所示。图1为计算得到的相图信息,从图中可知,本文计算结果与相关试验信息[5- 12]拟合良好。同时,利用EPMA技术测定了Fe2Ti相的相边界,从图1可以看出,试验结果与计算结果吻合较好。
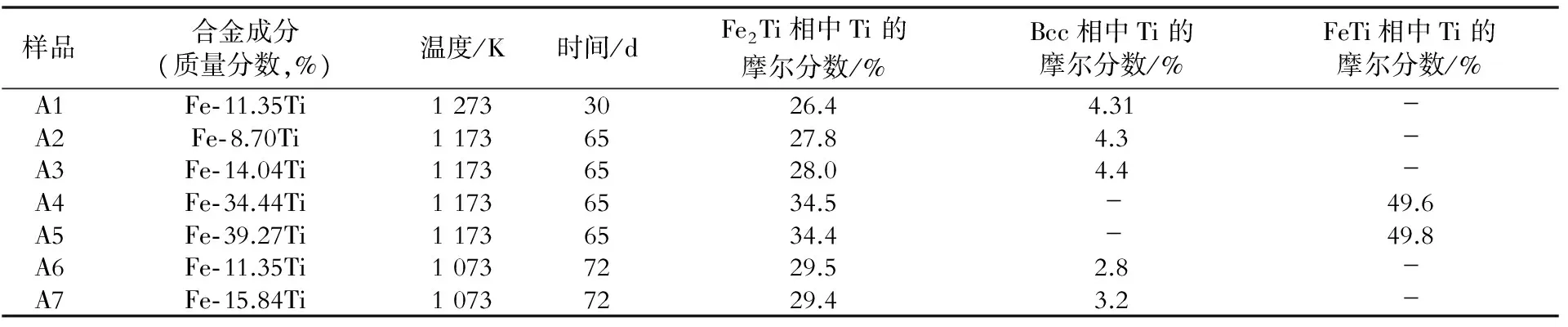
表1 实际合金成分、热处理工艺参数及EPMA测试结果Table 1 Terminal compositions of the alloys, heat treatment conditions and the results of EPMA

表2 优化得到的Fe- Ti- C热力学参数Table 2 Optimized thermodynamic parameters of Fe- Ti- C ternary system
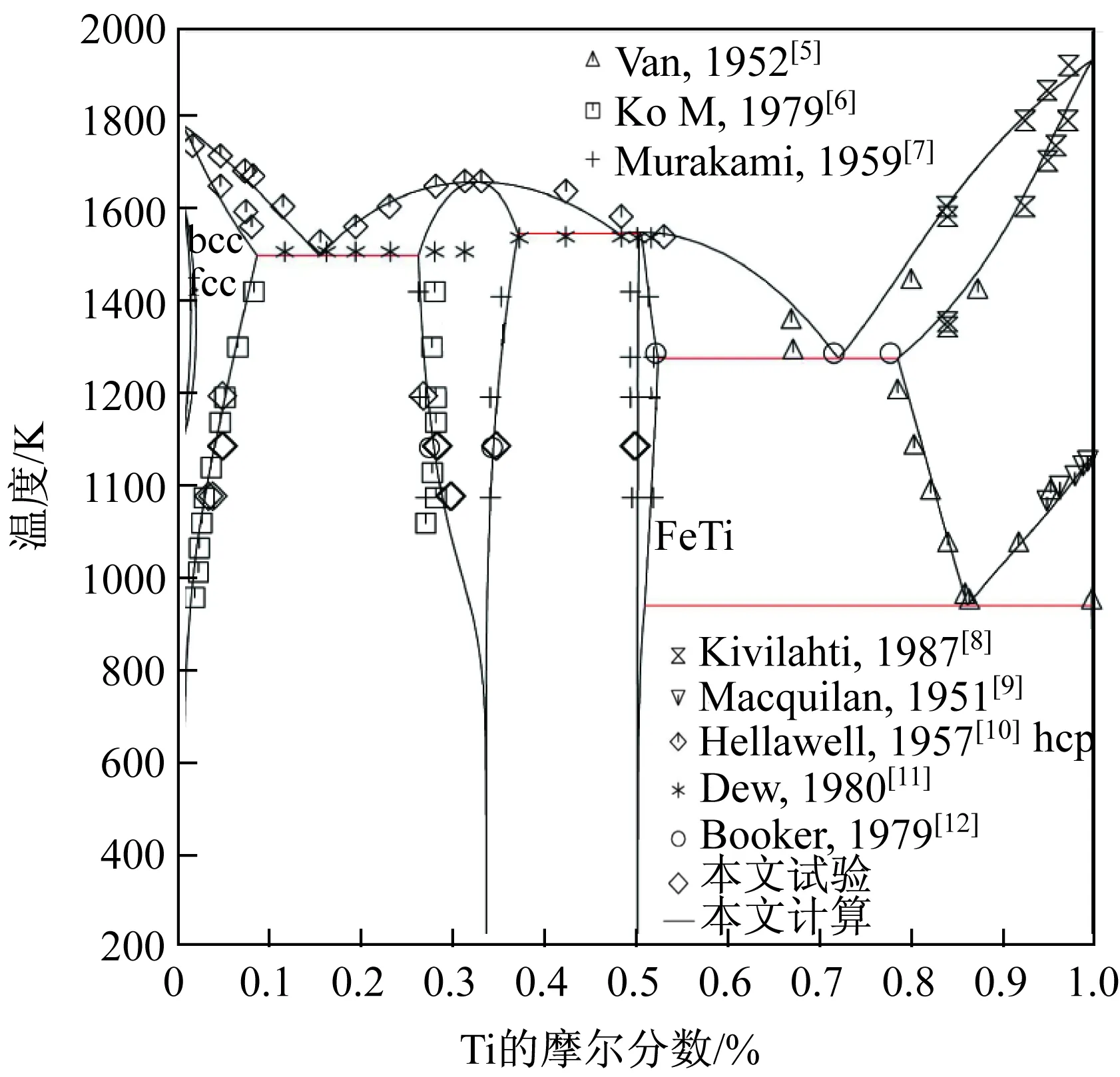
图1 Fe- Ti二元系计算相图与试验数据比较Fig.1 Comparison of the calculated phase diagram and the experimental data
对于富Ti端的相图信息,不同于Bo Hong等[4]的结果,本文依据最新试验数据[16]对热力学参数重新进行了优化评估,相图计算结果与相关试验信息[13- 16]如图2所示。
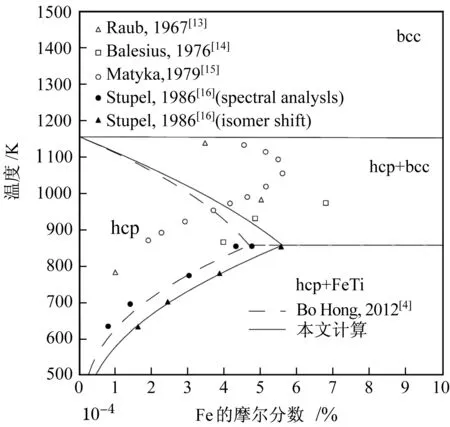
图2 富Ti端相图计算结果Fig.2 Calculated phase diagram of the Ti- rich side
许多学者[17- 20]对Fe- Ti体系的液相热力学性质进行了研究,结果较为一致。图3(a)为在1 873 K下Fe- Ti体系的液相形成焓计算结果与试验信息对比,两者拟合较好。图3(b)为2 000 K下液相混合偏焓的计算结果,在误差允许范围内,本文计算结果与Esin Y O等[20]的试验信息有较好的一致性。
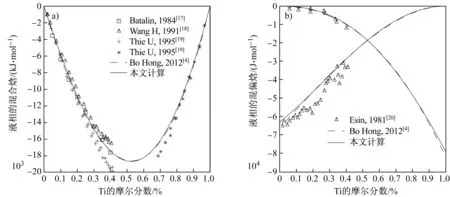
图3 Fe- Ti体系在1 873 K时的液相形成焓(a)和在2 000 K 时的液相混合偏焓(b)计算结果Fig.3 Calculated liquid enthalpy at 1 873 K(a) and partial enthalpy of mixing in the liquid at 2 000 K(b) for Fe- Ti alloy
研究发现,之前文献对于Fe2Ti和FeTi相形成焓的拟合效果并不理想。本文利用第一性原理方法计算得到Fe2Ti和FeTi相的端基自由能,并对该相的热力学参数重新优化,计算得到的形成焓值与试验数据[21- 23]吻合更好,如表3所示。图4为计算得到的Fe2Ti和FeTi相的热容,并与Bo Hong等[4]计算结果与Wang[24]的试验数据相比较,对比可见本文的计算结果与试验数据拟合得更好。
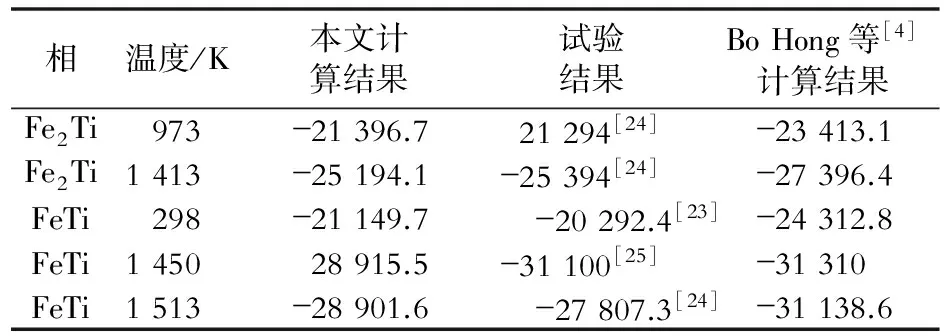
表3 计算得到的Fe2Ti和FeTi相的形成焓与试验值Table 3 Calculated enthalpy and the experimental data of Fe2Ti phase and FeTi phase
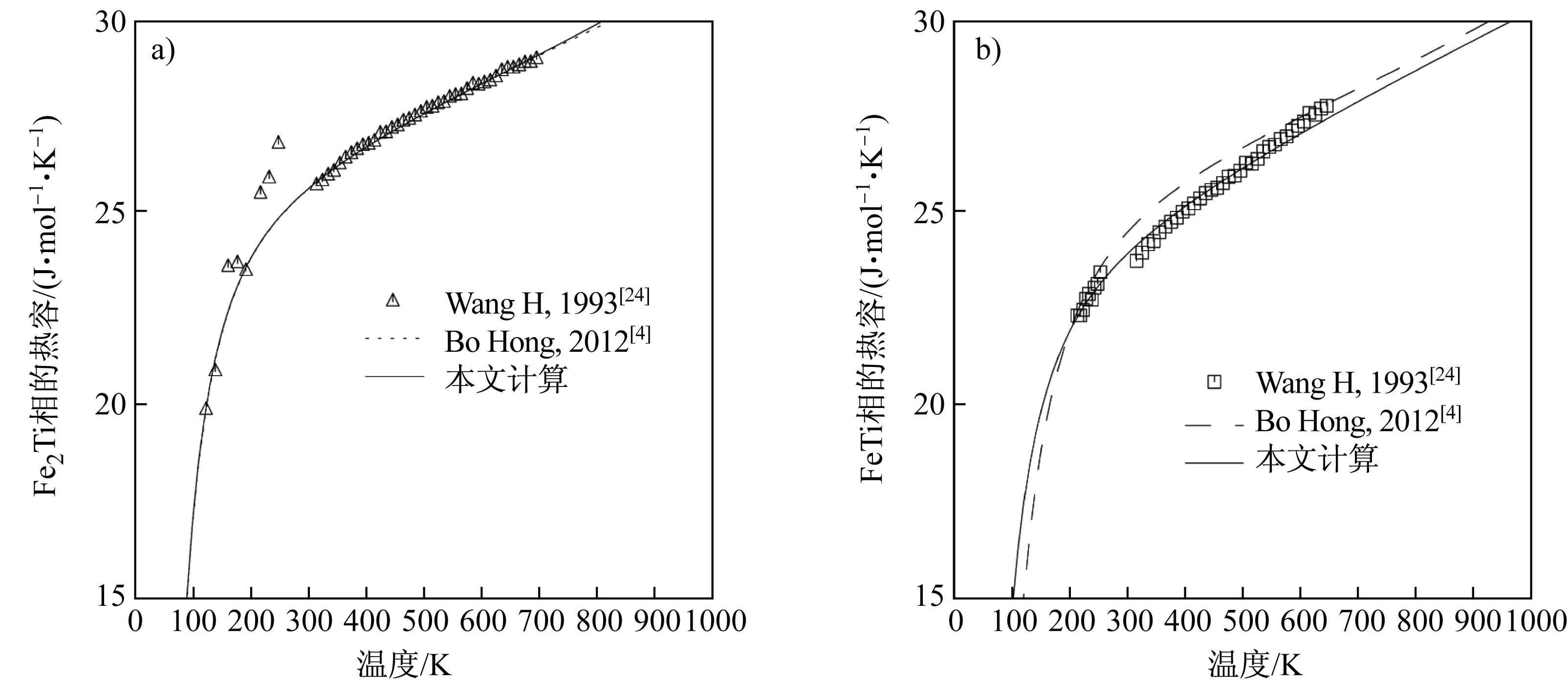
图4 计算得到的Fe2Ti(a)和FeTi相(b)的热容Fig.4 Calculated heat capacity of Fe2Ti phase (a) and FeTi phase (b)
众所周知,若要拟合优化某相的热力学参数,不能仅限于拟合相关相图数据,也要与该相的热力学数据吻合。研究发现,溶体相bcc缺乏热力学性质信息。为确保优化参数的合理性,本文利用第一性原理方法计算得到0 K时bcc相的形成焓,如图5所示,并与本文的计算结果(300 K)相比较。由图5可以看出,本文的计算结果与第一性原理结果有一些误差,但总体趋势一致。
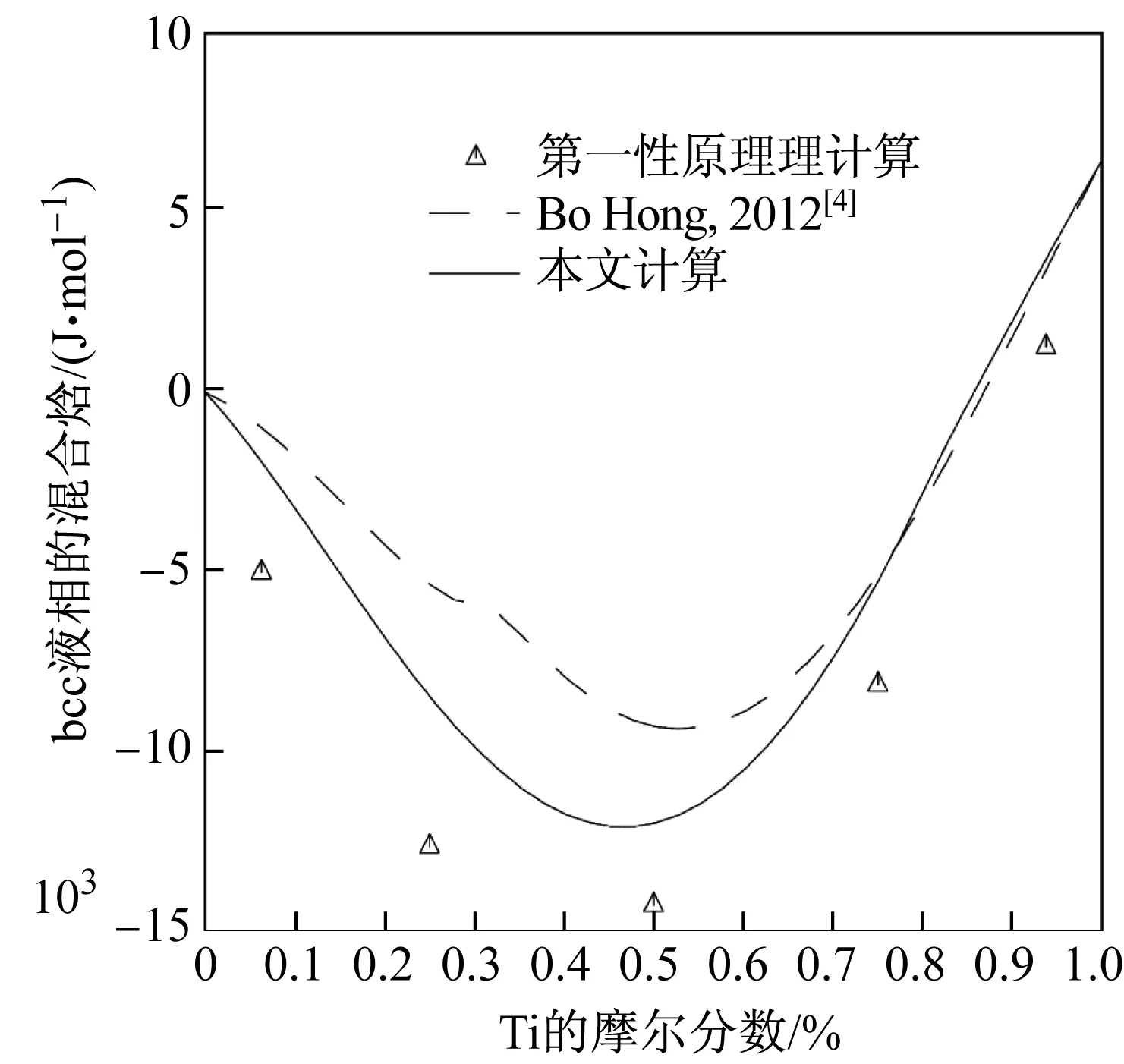
图5 计算得到的bcc相的形成焓和 第一性原理计算结果对比Fig.5 Calculated enthalpy of bcc phase compared with the ab- initio data
综上可知,本文根据Fe- Ti二元系的相图及热力学信息,利用CALPHAD方法同时结合第一性原理计算,优化得到一套合理的热力学参数。
3.2 Fe- Ti- C三元系热力学优化
通常,碳化物在奥氏体中的溶解度由碳的等活度线确定,其中等活度线的折点即被认为是碳化物的溶解度极限。Balasubramanian等[25]与Ohtani等[26]研究了1 273和1 473 K下碳在fcc(Fe)和fcc(Fe)与TiC相区中的等活度线,得到TiC在fcc(Fe)中的溶解度。本文采用现有的Ti- C和Fe- C二元系的热力学参数,并结合前述相关试验数据,优化了该三元热力学参数。图6为本文计算的TiC在fcc(Fe)中的溶解度与Dumitrescu等[27]的计算结果,由图可知本文较好地重现了现有试验信息,且比之前作者的优化结果更好。Ramaekers等[28]和Murakami等[29]研究了1 273 K下Fe- Ti- C体系的等温截面图,但Murakami的研究结果被后续学者证明是不合理的,所以本文在优化过程中并未考虑Murakami的试验信息,计算优化结果如图7所示。
研究发现Fe- Ti- C三元系中TiC在bcc相中的溶解度极低,所以本文在优化过程中未考虑TiC在bcc相中的溶解。
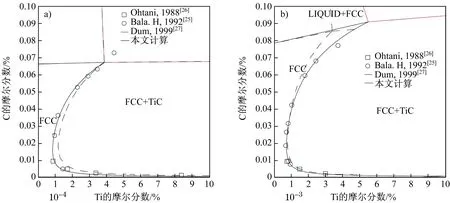
图6 1 273 K (a)和1 473 K(b)时TiC在fcc_Fe中的溶解度Fig.6 Calculated solubility of TiC in fcc_Fe phase at 1 273 K(a) and 1 473 K(b)
4 结论
本文通过对Fe- Ti二元系的相图信息、热力学数据及第一性原理计算结果进行严格评估,优化得到了一套较为满意的热力学参数。利用优化参数计算得到的FeTi、Fe2Ti和bcc相的形成焓与试验结果和第一性原理计算结果的吻合度较好。且bcc相的相界和富铁端fcc相的相界与试验结果拟合也更好。结合现有Ti- C和Fe- C二元系的热力学参数,通过拟合三元系相关试验数据,得到一套自洽的Fe- Ti- C三元系热力学参数。
Fe- Ti- C体系热力学数据库的优化建立,为后续钛钢复合板工艺参数的优化及扩散行为的模拟提供了理论基础。
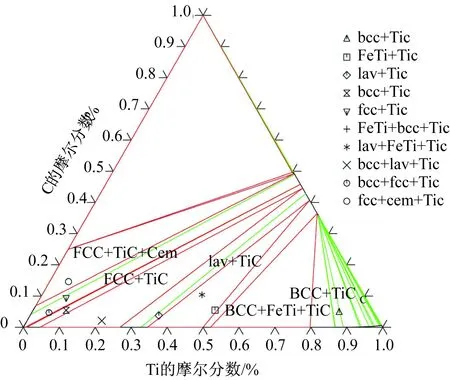
图7 1 273 K时Fe- Ti- C体系的等温截面图Fig.7 Calculated isothermal section diagram of Fe- Ti- C system at 1 273 K
致谢:
感谢国家973项目“先进金属基复合材料制备科学基础(No. 2012CB61960)”对本工作的支持。
[1] KIM J K, YU T X. Forming and failure behaviour of coated, laminated and sandwiched sheet metals: a review[J]. Journal of Materials Processing Technology, 1997, 63(1- 3): 33- 42.
[2] ANDERSSON J O, HELANDER T. Thermo- Calc & DICTRA, computational tools for materials science[J]. Calphad- computer Coupling of Phase Diagrams & Thermochemistry, 2002, 26(2): 273- 312.
[3] DINASDALE A. SGTE data for pure elements[J]. Calphad, 1991, 15(4): 317- 425.
[4] BO H, WANG J, DUARTE L, et al. Thermodynamic re- assessment of Fe- Ti binary system[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(9): 2204- 2211.
[5] VAN T, KESSLER H D, HANSEN M. The systems titanium- chromium and titanium- iron[J]. Trans ASM, 1952, 44: 974- 989.
[6] KO M, NISHIZAWA T. Effect of magnetic transition on the solubility of alloying elements in alpha iron[J]. J Jpn Inst Met, 1979,43(2): 118- 126.
[7] MURAKAMI Y, KIMURA H, NISHIMURA Y. An investigation on the titanium- iron- carbon system [J]. Trans Nat Res Inst Met, 1959,1(1): 7- 21.
[8] KIVILAHTI J K, TARASOVA O B. The determination of the Ti- rich liquidus and solidus of the Ti- Fe system[J]. Metall Trans A, 1987,18(9): 1679- 1680.
[9] MCQUILLAN A D. The application of hydrogen equilibrium- pressure measurements to the investigation of titanium alloy systems[J]. J Inst Metals, 1951, 79(5/6): 73- 88.
[10] HELLAWELL A, HUME- ROTHERRY W. The constitution of alloys of iron and manganese with transition elements of the first long period[J]. Phil Trans R Soc Lond A, 1957, 249(968): 417- 459.
[11] DEW- HUGHES D. The addition of Mn and Al to the hydriding compound FeTi: Range of homogeneity and lattice parameters[J]. Metall Trans A, 1980, 11(7): 1219- 1225.
[12] BOOKER P H. Ternary phase equilibria in the systems Ti- Fe- C,Ti- Co- C and Ti- Ni- C[D]. Beaverton, OR: Oregon Graduate Center, 1979.
[13] RAUB E, RAUB C J, ROESCHEL E. The α- Ti- Fe solid solution and its superconducting properties[J]. J Less Common Met, 1967, 12(1): 36- 40.
[14] BALESIUS A, GONSER U. Precision phase analysis[J]. J Phys Colloq, 1976, 37(C6): 397- 399.
[15] MATYKA J, FAUDOT F, BIGOT J. Study of iron solubility in α- titanium[J]. Scr Metall, 1979, 13(7): 645- 648.
[16] STUPEL M M, BAMBERGER M, RON M. The solubility of iron in α- titanium in the temperature range 360- 580℃[J]. J Less Common Met, 1986, 123(1/2): 1- 7.
[17] BATALIN G I, KURACH V P, STUDAVTSOVA V S. Enthalpies of mixing of Fe- Cr and of Fe- Ti melts[J]. Russ J Phys Chem, 1984, 58(2): 289- 291.
[18] WANG H, LUCK R, PREDEL B. Calorimetric determination of the enthalpy of mixing of liquid iron- titanium alloys[J]. Z Metallkd, 1991, 82(8): 659- 665.
[19] THIEDEMANN U, QIN J P, SCHAEFERS K, et al. Mixing enthalpy measurements of liquid Fe- Ti alloys by levitation alloying calorimetry and calculation of the thermodynamic properties of mixing[J]. ISIJ Int, 1995, 35(12): 1518- 1522.
[20] ESIN Y O, VALISHEY M G, ERMAKOV A F, et al. Partial and integral enthalpy of mixing of liquid Fe- Ti alloys[J]. Izv Akad Nauk SSSR Met, 1981, 48(3): 30- 32.
[21] KUBASCHEWSKI O, DENCH W A. The heats of formation in the systems titanium- aluminium and titanium- iron[J]. Acta Metallurgica, 1955, 3(4): 339- 346.
[22] DINSDALE A T, CHART T G, PUTLAND F H. Enthalpies of formation of binary phases in the Fe- Ni system[R]. Middlesex:National Physical Laboratory, 1985.
[23] GACHON J C, NOTIN M, HERTZ J. The enthalphy of mixing of the intermediate phases in the systems FeTi, CoTi, and NiTi by direct reaction calorimetry[J]. Thermochimica Acta, 1981, 48(1/2): 155- 164.
[24] WANG H, LüCK R, PREDEL B. Heat capacities of intermetallic compounds in the iron- titanium system[J]. Z Metallkd, 1993, 84(4): 230- 236.
[25] BALASUBRAMANIAN K, KROUPA A, KIRKALDY J S. Experimental investigation of the thermodynamics of the C- Fe- Ti austenite and the solubility of titanium carbide[J]. Metallurgical Transactions A, 1992, 23A(3): 709- 712.
[26] OHTANI H, TANAKA T, HASEBE M. Calculation of the Fe- C- Ti ternary phase diagram[J]. Calphad- computer Coupling of Phase Diagrams & Thermochemistry, 1988, 12(3): 225- 230.
[27] DUMITRESCU L F S, HILLERT M. Reassessment of the solubility of TiC and TiN in Fe[J]. ISIJ International, 1999, 39(1): 84- 90.
[28] RAMAEKERS P P J, FJJ L V, BASTIN G F. Phase relations, diffusion paths and kinetics in the system Fe- Ti- C at 1273 K[J]. Zeitschrift Fuer Metallkunde, 1985, 76(4): 245- 248.
[29] MURAKAMI Y, KIMURA H, NISIMURA Y. An investigation on the titanium- iron- carbon system[J].Trans. Nat. Res. Inst. Met., 1959, 1(1): 7- 21.

