基于相控神经网络的地震多属性储层厚度预测

刘　洋

(中国地质大学 地球科学学院，武汉 430074)

利用地震属性进行储层研究，在油气勘探开发中得到了广泛的应用[1]。其中利用地震属性包含的地层厚度信息[2-3]定量估算储层厚度，是储层预测的重要研究内容。A.R.Brown等[4]、D.B.Neff[5]、P.Connolly[6]等研究了利用地震走时与地震振幅属性相结合的储层厚度估算方法。这类方法主要利用地震走时信息，同时依据储层厚度对振幅的调谐效应，将地震振幅属性作为走时信息的补充，因此本质上是一定厚度范围内振幅属性厚度估算，应用范围受到限制。

近年来，利用地震多属性计算储层厚度得到越来越多的研究和应用。这些方法可以分为2类：线性方法和非线性方法。王世龙等[7]、王开燕等[8]研究了地震多属性预测储层厚度的线性方法，该类方法计算快捷、稳定；但是由于地震多属性与储层厚度在内的多种信息存在非线性关系，线性方法预测储层厚度难以保证精度。非线性算法以人工神经网络为代表，陆光辉等[9]、王婷等[10]研究了其在多属性预测储层厚度中的应用，取得了较好的效果。神经网络等非线性方法理论上能提高厚度预测的精度，但该类方法受训练样本种类和数量的影响较大，在钻井数量较少、分布不合理、缺少地质规律的支撑的情况下，预测结果虽然在井点精度高，但整体不能反映地质规律，甚至出现异常值[11]。为了解决常规神经网络算法受训练样本数量影响大而预测结果不稳定的问题，本文引入能够反映储层空间变化规律的沉积相信息，在沉积相的控制下增加训练样本，从而提出基于相控神经网络的地震多属性储层厚度预测方法，以达到提高预测结果精度和地质合理性目的。

1　方法原理

针对常规神经网络预测储层厚度方法精度高的优点和稳定性差的不足，提出相控神经网络的技术方法。通过地震-沉积相的分析，建立目标储层的沉积相，通过虚拟井实现沉积相对神经网络算法的控制和约束，在提高精度的同时提高算法的稳定性。

1.1　常规神经网络储层厚度预测方法

常规神经网络储层厚度预测算法，通过模拟人脑内神经单元及其结构，以井点地震属性为学习样本作为输入，储层厚度作为输出，将输入和输出按不同的连接方式组成网络建立模型，以一定的学习准则进行训练学习，从而并行执行解决问题，进而完成厚度预测。神经网络预测储层厚度的方法，能发现地震属性及组合与储层参数隐含的非线性关系，从而有效地提高储层厚度预测精度[12]。但在钻井较少、砂体变化快的情况下，由于学习样本数量、种类的不足和空间分布的不合理，会导致计算结果不稳定，出现整体分布特征不合理的现象。

1.2　基于相控神经网络的储层厚度预测方法

1.2.1研究思路与技术流程

针对常规神经网络储层厚度预测方法存在的问题，本文提出了相控神经网络地震多属性预测储层厚度的方法，其研究思路是在沉积地质学理论的指导下丰富学习样本，提高样本空间分布的合理性，从而提高神经网络算法的精度、稳定性和空间合理性。方法的技术流程如图1所示，关键技术环节有：①通过地震-沉积相分析，划分研究目标的相带；②使用线性方法初步估算储层厚度；③依据相带分布建立相控网格；④相控神经网络厚度估算，优选地震属性，将相控样本网格作为训练样本，利用人工神经网络算法预测储层厚度。

1.2.2地震-沉积相分析

通过正演模拟等方法，研究储层及其关键属性(物性、含油气性)的地震响应特征，找到能够稳定反映储层变化的敏感地震属性；通过井震标定，找到目标储层对应敏感地震属性在空间中的位置；与常规地震剖面结合，追踪解释储层顶(或底)界面，利用追踪层位，提取敏感地震属性的沿层切片；检验地震属性切片反映的储层分布特征是否与单井相和区域沉积认识吻合，如果不吻合则重新进行“属性优选—砂体解释—属性提取—分析验证”工作，如果吻合则作为沉积相的建立依据，划分研究区目的层的相带空间分布。

1.2.3相控网格建立与神经网络储层厚度计算

相控样本网格，是依据“相带空间分布”，通过虚拟井和已钻井数据建立的神经网络训练样本库，在此基础上实施神经网络算法计算储层厚度。其计算流程如图2所示。

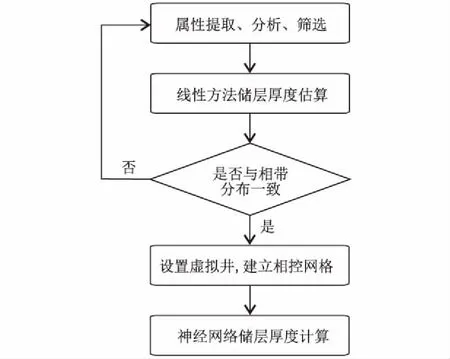
图2　相控神经网络计算流程Fig.2　Calculation process of facies-guided neural network

a.地震属性提取、分析、筛选：在对工区地震资料做优化处理后，依据井震标定提取目标层多种属性并进行标准化处理；在此基础上，通过对地震属性的相关性分析和聚类分析，优选出一组相关性适中的属性组合。

b.用线性方法估算储层厚度：利用优选的地震属性和已钻井数据，通过多元线性回归初步估算储层厚度。

c.初算厚度分析：检验初算结果是否与研究目标的相带分布规律一致，如果不一致则重复步骤a和b，如果一致则作为虚拟井的数据来源。

d.设置虚拟井，建立相控网格：根据前人研究[13-14]，结合相控提高神经网络算法稳定性的目的。虚拟井的设置遵循如下原则：①虚拟井分布尽可能均匀；②虚拟井在不同相带上都有分布，在不同相的过渡带适当增加虚拟井，在实际钻井数据较多的相带上适当减少虚拟井；③虚拟井尽可能位于地震属性信噪比高和初算厚度稳定的位置；④虚拟井在模型中的权重较实钻井低。依据上述原则设置好虚拟井，提取初步估算厚度，与钻井数据构成相控样本网格。

(1)

(2)

2　应用实例

2.1　工区背景

研究区H气田位于东海陆架盆地西湖凹陷，主要目的层G1气藏埋藏比较深，为孔隙度比较低的低孔渗储层。气田内有钻井5口，钻井揭示该气田花港组目的层为浅水环境的水下分流河道、河口坝沉积，砂体横向变化快[16]，5口钻井在主要目的层G1气藏钻遇的砂体厚度、孔隙度、含水饱和度等参数均有差异。为合理准确地计算气田的储量，以及为气田开发地质建模等研究做准备，需要合理估算储层厚度等参数的空间分布。在地质沉积分析和地震多属性提取分析的基础上，应用相控神经网络方法估算了G1气藏储层厚度的空间变化。

2.2　沉积相带划分

根据目标储层为低孔渗砂岩的特点，通过正演模拟研究了储层及其孔隙度和孔隙流体的地震反射特征。图3-A为含水饱和度不变、不同孔隙度条件下的叠加剖面，从图中可以看出，随着孔隙度的增大，砂岩顶面(蓝色虚线)的反射逐渐由正变负，相位出现变化，因此常规叠加剖面的振幅属性受物性影响大，不能作为反映岩性变化的敏感属性。图3-B为不同孔隙度条件下的AVO梯度剖面(振幅随偏移距的变化率[17])，在AVO梯度剖面上，随孔隙度的变化，梯度值变化，但相位不变(均为负值)，因此岩性对AVO梯度的影响大于物性。再来看孔隙流体对AVO梯度的影响，图3-C为孔隙度不变、不同含水饱和度条件下的AVO梯度剖面，随着含水饱和度的增大， 砂岩顶面AVO梯度保持负相位不变，说明孔隙流体对AVO梯度的影响小于岩性。通过以上分析可以得到如下结论：AVO的梯度信息主要是岩性界面的响应，是本地区的储层敏感属性。

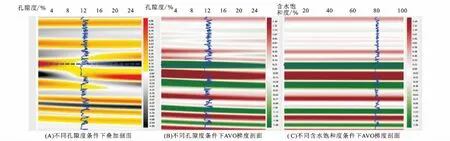
图3　储层地震响应分析Fig.3　Analysis of reservoir seismic response

图4为AVO梯度属性的联井剖面，从图中可以看出，G1气藏顶界面标定在AVO梯度的负相位上，与砂岩顶面的地震响应吻合。提取砂岩顶面的AVO梯度最小值如图5所示，其平面特征表现为北东向的水道特征，与目的层区域沉积特征和单井相分析吻合。应用AVO梯度属性进行地震-沉积相分析，将研究区目的层划分为分流河道主体、分流河道侧缘、分流间湾、沼泽4种相(图6)。

2.3　储层厚度估算

在地震资料优化处理的基础上，提取了17种地震属性并进行了标准化，通过聚类分析与相关性分析，优选出了最小振幅、弧长、能量半衰时和均方根振幅(图7)4种属性用于多元线性回归砂岩厚度预测(图8)。预测结果与钻井基本吻合，精度较高(图9)。砂岩预测厚度与相带空间分布规律基本一致，多元线性回归预测结果可以作为虚拟井的数据来源。

结合已有钻井分布和相带划分，在线性方法储层厚度估算结果上提取了9口虚拟井，用于丰富神经网络算法的学习样本(虚拟井位置如图8所示)。在此基础上，利用神经网络计算的储层厚度图10所示。对比5口井作为样本的常规神经网络方法(图11)，相控神经网络在提高精度的同时(图12)，保持了储层厚度空间分布的合理性。

图4　H气田AVO梯度联井剖面Fig.4　Joint well profile of AVO gradient of the H gas field

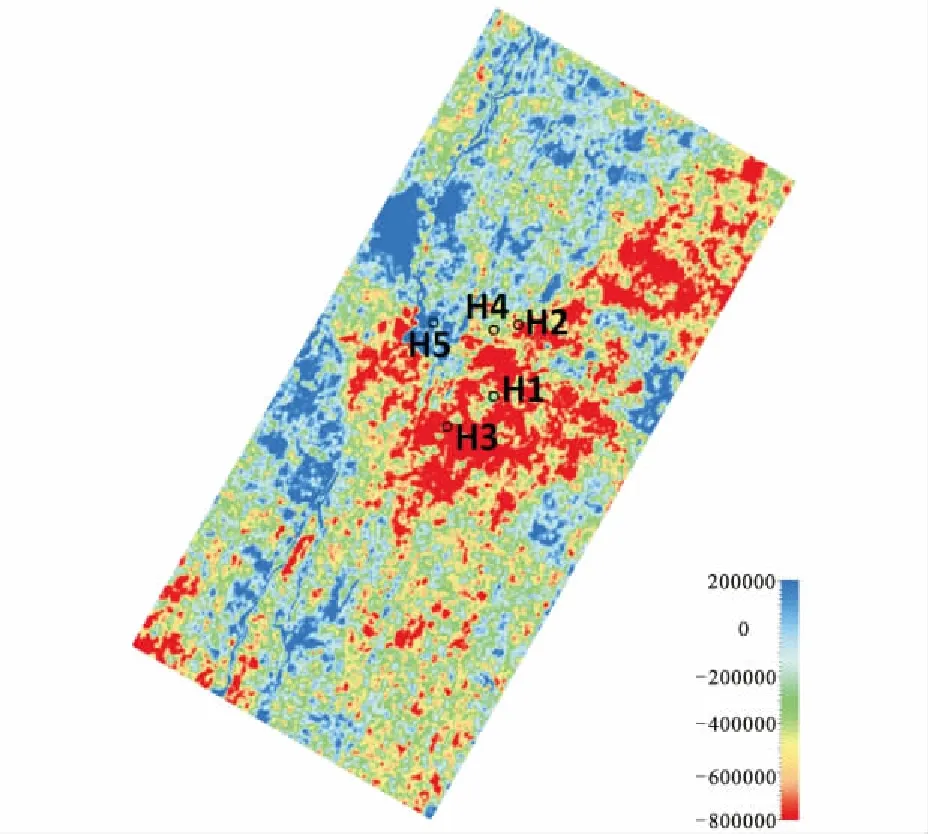
图5　G1气藏AVO梯度最小值Fig.5　Minimum value of AVO gradient of G1 reservoir

图6　G1气藏空间相带划分Fig.6　Classification of facies of the G1 reservoir

图7　G1气藏线性拟合优选地震属性Fig.7　Seismic attribute optimization by linear fitting of G1 reservoir

图8　G1气藏多元线性回归储层厚度预测建立相控约束网格Fig.8　Facies-guided grid established by multiple linear regressions for reservoir thickness prediction of G1 reservoir

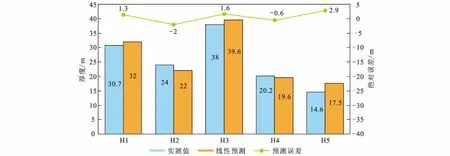
图9　线性预测误差对比分析Fig.9　Comparison analysis of linear prediction error

图10　相控神经网络法预测G1气藏厚度Fig.10　Facies-guided neural network prediction of the G1 reservoir thickness

图11　常规神经网络法预测G1气藏厚度Fig.11　Normal neural network prediction of the G1 reservoir thickness

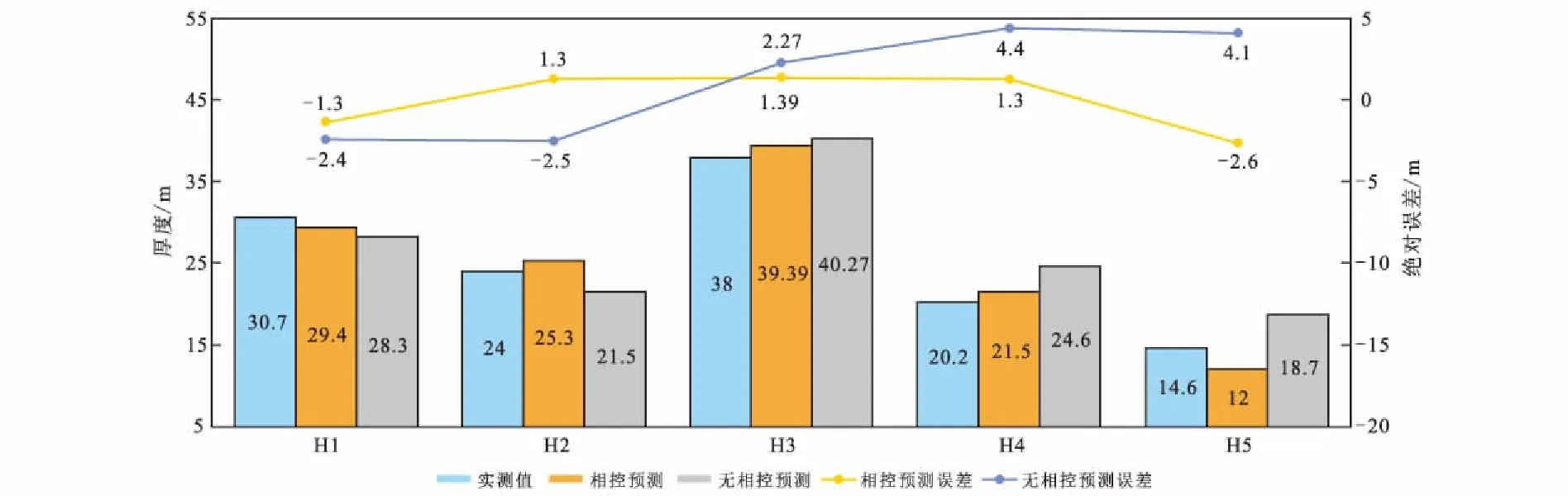
图12　误差对比分析Fig.12　Error comparison analysis

3　结 论

a.人工神经网络方法能够反映地震属性和储层厚度之间的非线性关系，从而提高储层厚度预测精度；但是在学习样本种类或数量不够的情况下，计算的结果不稳定，不能反映地质规律。

b.本文提出的基于相控神经网络的储层厚度预测技术，基于相控神经网络地震多属性储层厚度预测方法，在地震-沉积研究的基础上，划分能够反映储层宏观变化规律的空间相带；在相带的指导下设置虚拟井，与实际钻井样本点结合建立相控网格，丰富神经网络训练样本的数量、类型和空间分布，应用人工神经网络算法通过对样本点的训练进行地震多属性储层厚度的预测。该技术在提高预测精度的同时，提高了预测的空间稳定性，预测结果符合地质规律。

c.实际工区目标储层为三角洲平原的水下分流河道，砂体变化快，基于相控神经网络厚度预测结果较常规方法提高了精度，厚度分布特征与地质认识一致。

[参考文献]

[1] Chopra S, Marfurt K J. Seismic attributes — A historical perspective [J]. Geophysics, 2005, 70: 3SO-28SO.

[2] Connolly P, Kemper M. Statistical uncertainty of seismic net pay estimation [J]. The Leading Edge, 2007, 26: 1284-1289.

[3] 赵虎，尹成，彭达，等.砂泥岩储层间距变化对地震属性影响分析[J].地球物理学进展，2013,28(2):899-907.

Zhao H, Yin C, Peng D,etal. Analyze the relationship of seismic attributes and sandstone and mudstone reservoir distance changes [J]. Progress in Geophysics, 2013, 28(2): 899-907. (in Chinese)

[4] Brown A R, Wright R M, Burkart K D,etal. Interactive seismic mapping of net producible gas sand in the Gulf of Mexico [J]. Geophysics, 1984, 49: 686-714.

[5] Neff D B. Estimated pay mapping using three-dimensional seismic data and incremental pay thickness modelling[J]. Geophysics, 1990, 55: 567-575.

[6] Connolly P. A simple, robust algorithm for seismic net pay estimation [J]. The Leading Edge, 2007, 26: 1278-1282.

[7] 王世龙,周妍,王开燕.基于偏最小二乘回归法的储层厚度预测[J].复杂油气藏,2015,8(1)：7-10.

Wang S L, Zhou Y, Wang K Y. Prediction of reservoir thickness based on partial least squares regression method[J]. Complex Hydrocarbon Reservoirs, 2015, 8(1): 7-10. (in Chinese)

[8] 王开燕，周妍，陈彦奇，等.基于谱分解和地震多属性储层厚度的预测[J].地球物理学进展，2014,29(3):1271-1276.

Wang K Y, Zhou Y, Chen Y Q,etal. Prediction of reservoir thickness based on spectral decomposition and seismic multi-attribute [J]. Progress in Geophysics, 2014, 29(3): 1271-1276. (in Chinese)

[9] 陆光辉，吴官生，朱玉波，等.地震属性信息预测储层厚度[J].河南石油，2003, 17(2):10-12.

Lu G H, Wu G S, Zhu Y B,etal. Prediction of reservoir thickness by seismic attribute information[J]. Petroleum Geology and Engineering, 2003, 17(2): 10-12. (in Chinese)

[10] 王婷，杨斌，杨勇，等.利用BP神经网络预测储层参数[J].辽宁化工，2013,42(2):160-163.

Wang T, Yang B, Yang Y,etal. Calculation of reservoir parameters by using the BP neural network[J]. Liaoning Chemical Industry, 2013, 42(2): 160-163. (in Chinese)

[11] Mirko van der Baan, Jutten C. Neural networks in geophysical applications [J]. Geophysics, 2000, 65: 1032-1047.

[12] Poulton M M. Neural networks as an intelligence amplification tool: A review of applications [J]. Geophysics, 2002, 67: 979-993.

[13] 刘超，谢传礼，李宇鹏，等.利用虚拟井提高相控随机模型中地质约束的原理和方法[J].天然气地球科学，2015,26(4)：616-624.

Liu C, Xie C L, Li Y P,etal. The principle and method of improving geological constraint in facies-guided random model with virtual well [J]. Natural Gas Geoscience, 2015, 26(4): 616-624. (in Chinese)

[14] 李培培，刘志国，杨松岭，等.虚拟井技术在无井或少井条件下时深转换中的应用[J].物探与化探，2015,39(5)：994-1000.

Li P P, Liu Z G, Yang S L,etal. The application of virtual well technique to time-depth conversion under the condition of no or few wells [J]. Geophysical and Geochemical Exploration, 2015, 39(5): 994-1000. (in Chinese)

[15] Hampson D P, Schuelke J S, Quirein J A. Use of multiattribute transforms to predict log properties from seismic data [J]. Geophysics, 2001, 66: 220-236.

[16] 姜勇,李宁,涂齐催.基于叠前同步反演的储层参数预测技术研究及应用[J].油气藏评价与开发，2016,6(1)：9-13.

Jiang Y, Li N, Tu Q C. Study on reservoir parameters prediction technique based on pre-stack simultaneous inversion and its application[J]. Reservoir Evaluation and Development, 2016, 6(1): 9-13. (in Chinese)

[17] Shuey R T. A simplification of the Zoeppritz equations [J]. Geophysics, 1985, 50: 609-614.